H形截面钢构件铰区模型及铰区长度
程 欣, 陈以一
(1. 太原理工大学 建筑与土木工程学院, 山西 太原 030024; 2. 同济大学 土木工程防灾国家重点实验室, 上海 200092)
H形截面钢构件铰区模型及铰区长度
程欣1, 2, 陈以一2
(1. 太原理工大学 建筑与土木工程学院, 山西 太原 030024; 2. 同济大学 土木工程防灾国家重点实验室, 上海 200092)
摘要:将局部失稳的集中区域定义为铰区.提出了由局部失稳控制破坏模式的H形截面铰区平均曲率的计算公式.发现铰区长度主要依赖于截面构型及轴力大小,用归纳方法得到了考虑不同截面构型及加载条件影响的铰区长度计算方法.实现了从H形截面悬臂钢构件模型中提取扣除计算长度影响的截面层次的弯矩-曲率关系.该弯矩-曲率关系作为不同受力形式、不同构件长度及边界条件的构件非线性分析的基础,可提高结构体系非线性分析的分析效率,并满足工程研究的精度要求.
关键词:压弯构件; 铰区模型; 平均曲率; 铰区长度; 弯曲变形
悬臂构件受常轴压力及水平侧向力作用是研究框架柱构件抗震性能的最基本加载模式之一[1].然而框架柱受力形式复杂多样,以悬臂构件为基本单元的弯矩-弦转角力学模型只适用于特定弯矩梯度和特定构件长度的情况,不能直接应用于构件受力形式或长度发生改变的情况[2].要得到不同长度及边界条件的构件或结构体系的非线性反应,需基于截面层次的力学计算模型.
截面的力学性能主要通过弯矩-曲率(M-φ)关系来表征,因此截面M-φ模型是进行框架结构体系非线性分析的重要基础.影响M-φ关系的主要影响因素较多,将这些因素考虑进M-φ模型是难点,也一直是国内外的研究热点[3-5].
本文通过提出铰区的概念,阐述了如何从悬臂钢构件模型中提取出扣除构件计算长度影响的截面层次的弯矩-曲率关系.该方法可为得到反映材料强化作用、局部屈曲引起的各项退化、板件屈曲相关作用等截面层次的弯矩-曲率恢复力模型提供计算基础.
1结构体系非线性计算方法
要得到不同长度及边界条件的构件或结构体系的非线性反应,需基于截面层次的力学计算模型.具体操作方法为:将一根构件沿轴线方向划分若干个构件段,每个构件段作为一个单元,通过数值迭代计算法,可获得各种边界条件和加载条件下构件的非线性反应,进而得到钢框架的非线性反应,如图1所示.对于由局部失稳控制破坏模式的H形截面力学性能的研究一般需以构件层次的试验或有限元模型为载体[6-9],而要得到截面的M-φ计算模型,首先需要从构件力-位移曲线中得到提取扣除构件长度影响的M-φ曲线,本文即对该问题展开研究.
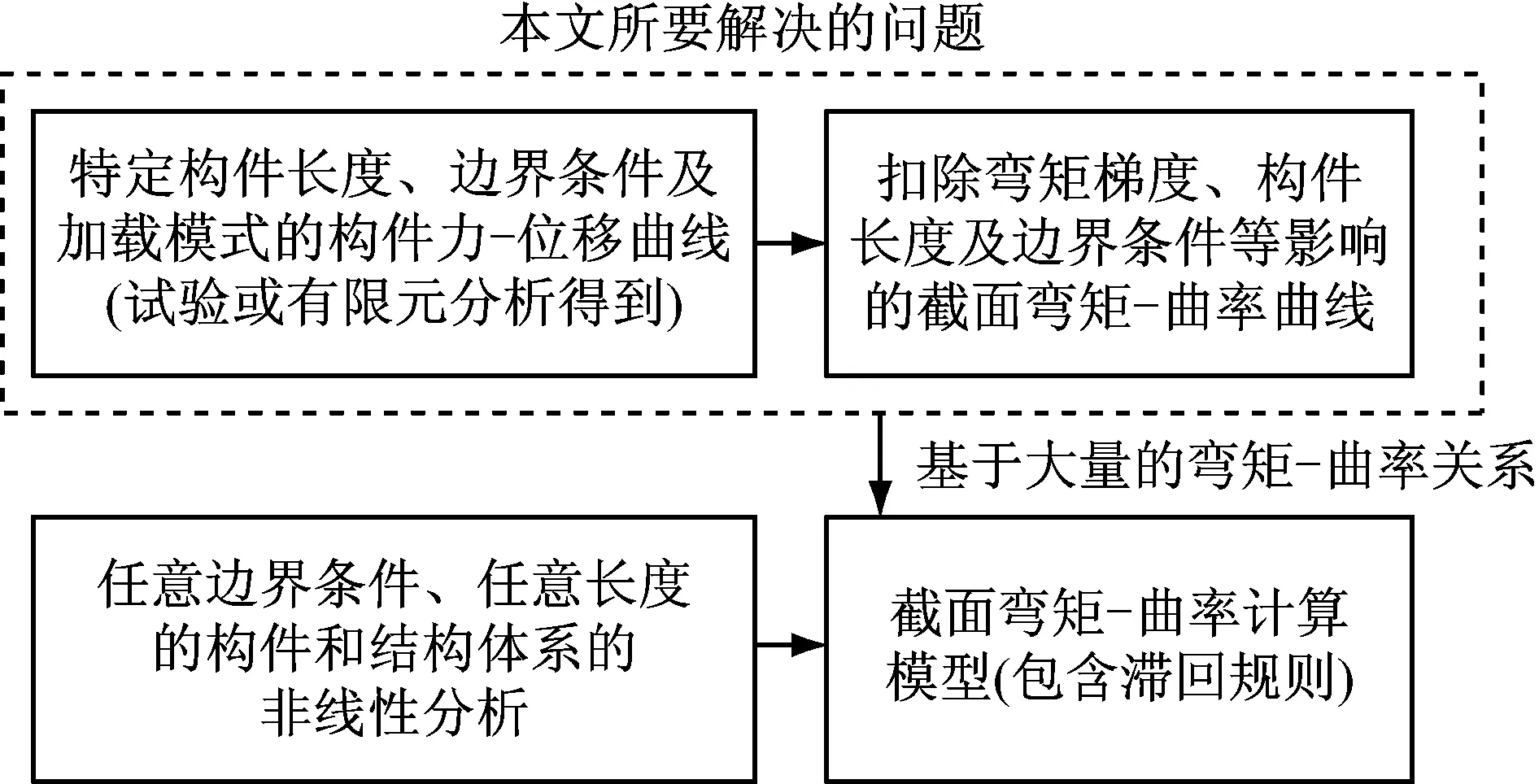
图1 结构体系非线性计算方法
2铰区受力与变形
2.1铰区定义
以板件宽厚比较大的H形截面钢构件为研究对象的试验及理论研究[7-10]均显示,构件弯矩最大部位是构件塑性和局部屈曲变形的集中域,随着塑性变形或局部屈曲的发生及发展,该区段在弯矩作用下发生转动,形成类似“铰”的性能.图2以文献[8]中的试件S-H4-0.2为例,显示了H形悬臂钢构件局部屈曲变形的发展过程.可以看到,构件根部的翼缘及腹板均发生了明显的局部鼓曲,且鼓曲的部位始终集中在一定的范围内.局部鼓曲区段是各种非线性的综合段,屈曲发生后,板件偏离原平衡位形,平截面假定失效,鼓曲段内部的力学性能非常复杂,因此需将鼓曲段作为一个整体进行描述.
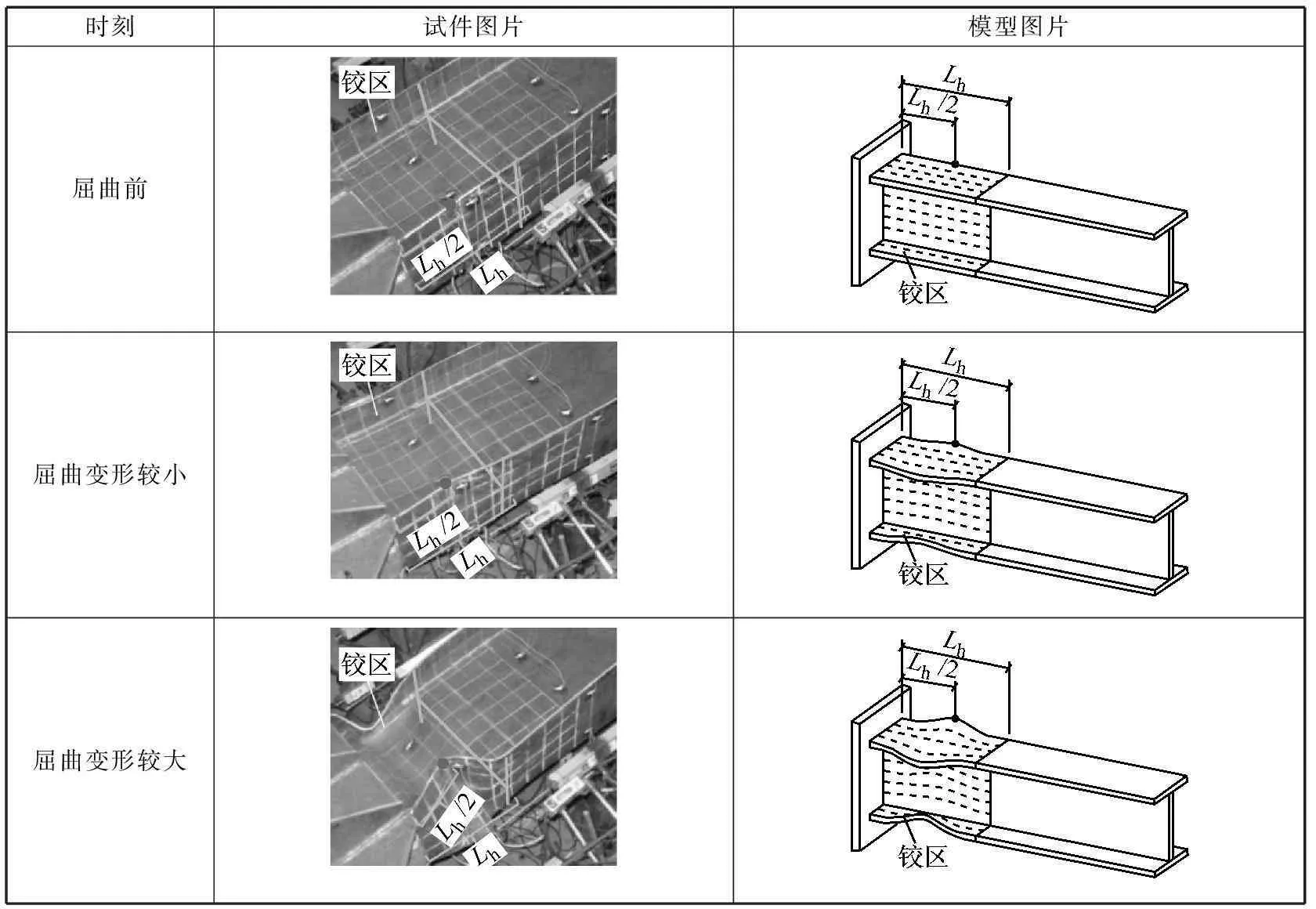
时刻试件图片模型图片屈曲前屈曲变形较小屈曲变形较大
图2试件S-H4-0.2变形发展模式[8]
Fig.2Deformation development mode of specimen S-H4-0.2[8]
将局部屈曲发生的基本单元作为一个“铰区”(hinge zone),铰区的受力特性如图3a所示.铰区具有以下特点:具有一定的转动能力;有一定的长度区域;铰区的力学性能可由弯矩-转角曲线进行描述;通过采用铰区的弯矩-平均曲率模型,将铰区作为压弯构件的基本单元.
本文的研究基于以下3个假定进行:
(1)不考虑铰区剪切变形的影响.
(2)铰区自身的挠曲变形可忽略不计.
(3)构件无整体弯扭失稳.
2.2铰区与悬臂构件的关系
图2表现了局部失稳控制破坏模式的悬臂构件与铰区之间的关系.对于悬臂构件,构件端部为弯矩作用最大区域,是局部屈曲变形的集中区域,即为铰区段.构件其余部位弯矩作用较小,在加载过程中保持弹性,称其为“弹性段”,弹性段的变形满足平截面假定.
悬臂构件由铰区和弹性段组成,两部分通过一个平截面过渡,标记铰区的长度为Lh,弹性段长度为Les,如图4a所示.悬臂构件的宏观变形包括自由端的水平位移Δ及竖向位移w,如图4b所示,可分解为弹性段变形(图4c)及铰区变形(图4d).求解弹性段变形时,将铰区看作是无变形的刚体;而在求解铰区变形时,将弹性段看成刚体.本文主要关注的铰区弯曲变形,可从悬臂构件扣除弹性段的变形得到.
2.3铰区受力
铰区的受力形式如图3a所示,铰区受到弯矩M、轴力N及剪力V的作用.基于铰区长度较小的假定,忽略铰区长度范围内弯矩梯度的影响,且假定铰区承受的弯矩大小等于铰区的最大弯矩.对悬臂构件顶部受竖向力及水平侧向力的加载形式而言,铰区的弯矩可取悬臂构件柱底弯矩,铰区弯矩M的表达式为
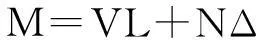
(1)

a 铰区受力与变形特点
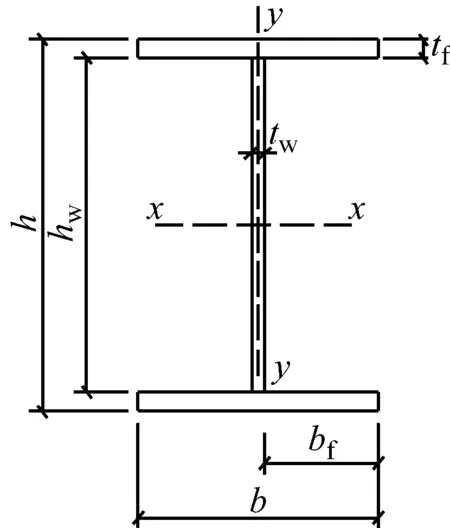
b H形截面尺寸定义
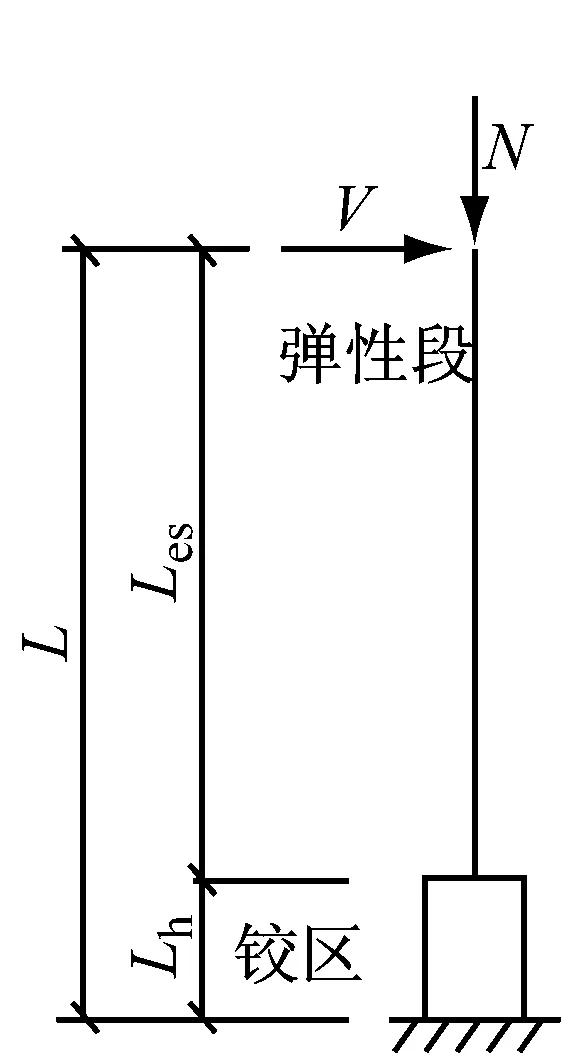
a 变形前
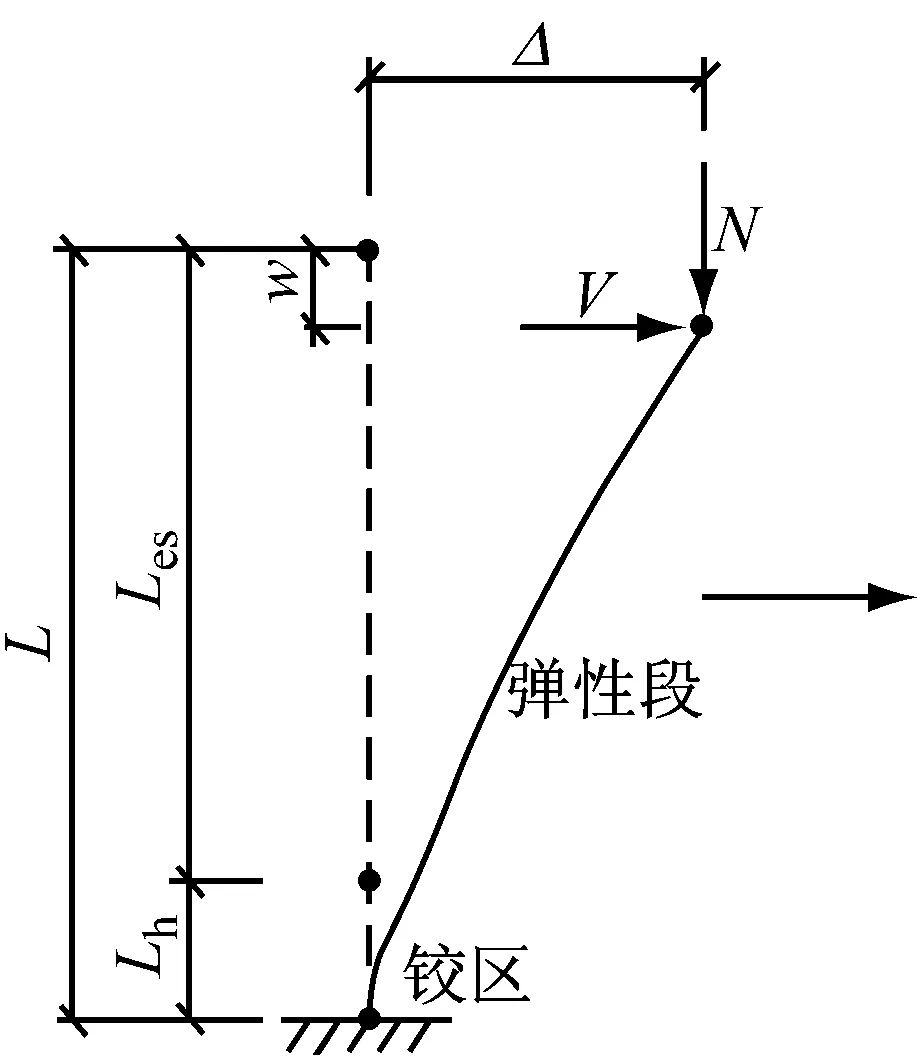
b 悬臂构件变形

c 弹性段变形
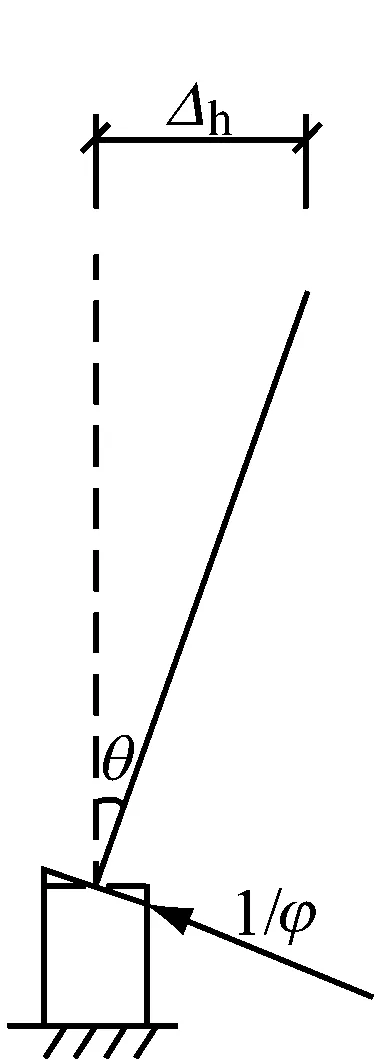
d 铰区变形
2.4铰区弯曲变形
由图4可知,悬臂构件的水平位移Δ由弹性段水平位移Δes和铰区变形导致的水平位移Δh组成,不考虑剪切变形的影响,Δh为铰区的转动带动弹性段转动产生的水平位移,有
(2)
(3)
式中:θ为铰区的转角.
不妨假定铰区长度Lh范围内的曲率相等,则铰区平均曲率φ可表示为
(4)
式中:L为悬臂构件的长度;Δ为悬臂构件加载点水平位移,可从悬臂构件计算结果中直接提取;Δes为弹性段的水平位移,可根据弹性理论直接计算求得.
注意到铰区转动产生的自由端水平位移Δh、铰区的转角θ及铰区的平均曲率φ均是铰区弯曲转动不同的表现形式,三者呈线性关系,本质上表征的是同一概念.
本文的研究目的是从特定长度、特定受力条件及特定边界条件的构件力-位移曲线中提取出扣除构件长度及受力条件影响的截面层次的M-φ曲线,为任意长度、任意受力条件及任意边界条件的构件模型提供理论基础.铰区作为局部屈曲控制破坏模式的截面层次的综合体现,铰区的平均曲率φ可认为是截面性能的体现,可作为截面变形性能的主要形式.
根据公式(1)和(4)即可得到扣除构件计算长度影响的H形截面层次的M-φ曲线.不考虑构件弯矩作用平面外弯扭失稳的影响,以此得到的M-φ模型适用于任意长度的悬臂构件绕任一截面主轴弯曲或压弯的情况.
3铰区长度的确定
由式(4)可知,要得到铰区的平均曲率φ,还需确定铰区长度Lh,由此可见Lh为铰区模型的关键,本节将给出Lh的计算公式.
3.1铰区长度的确定方法
根据定义,铰区为局部屈曲发生的基本单元,在特定的加载条件下,屈曲变形的形式基本不发生变化,屈曲变形的幅值随着外荷载的增大而增大,如图2所示.可认为铰区板件屈曲波形的波峰或波谷至构件根部的距离为一半的铰区长度,即Lh/2,从而能较为准确的确定出铰区的长度.
图5显示了文献[8]中试件H5在不同轴压比(n=0.2和0.4)作用下绕强压弯的试验及相应的有限元模型变形图.图5中,试件编号为S-H5-n,其中S表示绕强轴弯曲,试件H5尺寸为H300 mm×200 mm×4 mm×6 mm,n为轴压比;铰区长度单位为mm.以此为例给出了本文试验及有限元模型铰区长度的确定方法,即通过找到局部屈曲变形的最大位置,确定Lh/2.其中有限元模型的建立方法参见文献[11-12].可以发现,有限元模型与试验得到的铰区长度基本一致,说明有限元模型能够较好地体现铰区长度.
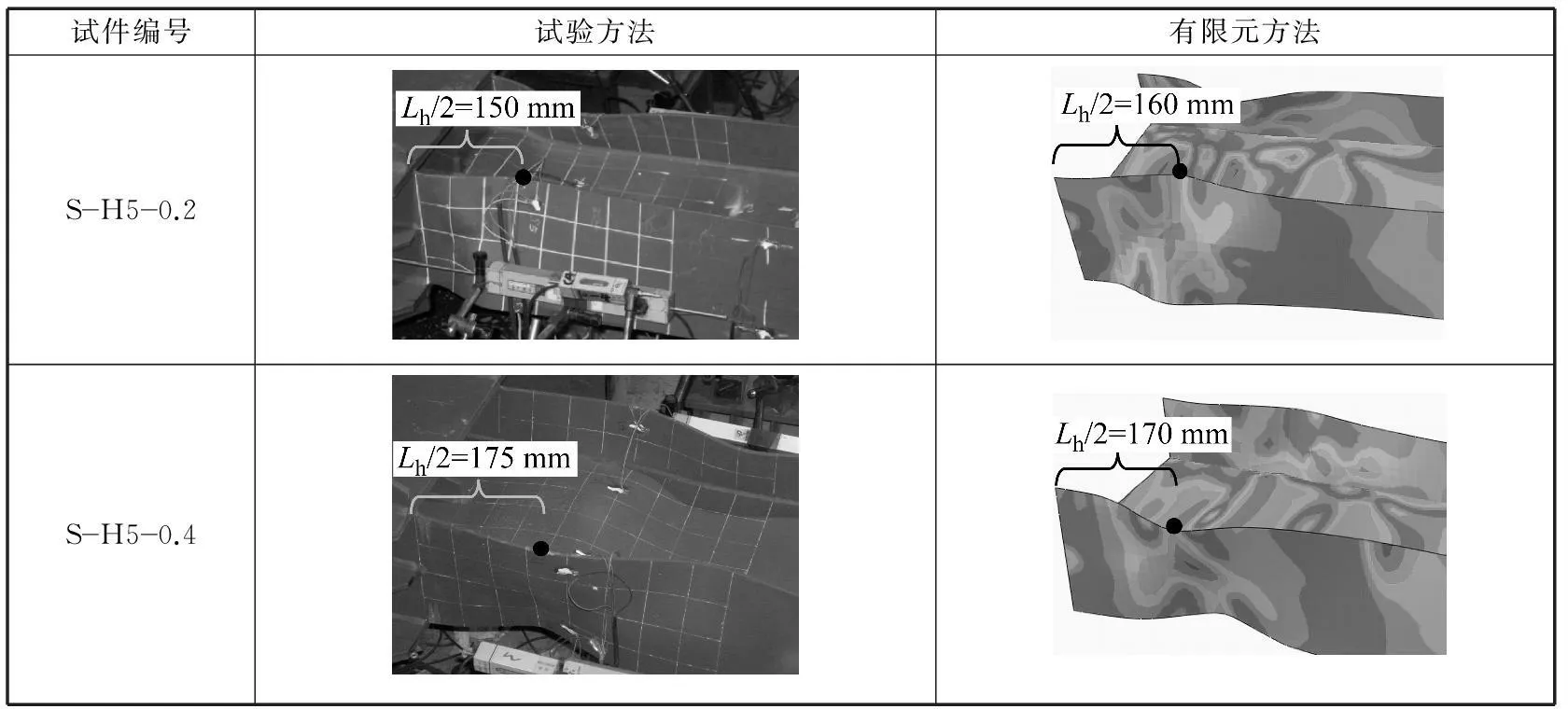
试件编号试验方法有限元方法SH50.2SH50.4
图5试验与有限元铰区长度对比
Fig.5Comparsions of hinge zone length in test and FEM
3.2铰区长度与构件长度及弯矩梯度的关系
为考察构件长度或铰区弯矩梯度对铰区长度Lh的影响,对同一截面尺寸(H300 mm×200 mm×4 mm×6 mm)不同构件长度(L=500,1 000,1 500,2 000和2 500 mm),受常轴压力(n=0.2),分别绕强、弱轴压弯的10个悬臂构件模型进行了有限元分析,受力形式如图4a所示.根据2.1节的方法,分别提取出各构件模型的Lh/2,列于图6中.可以看到,对于不同长度的构件模型,铰区长度基本保持在同一水平,说明构件长度对铰区长度Lh的影响较小.同时也注意到同一构件模型绕不同截面主轴压弯时,铰区长度差别较大,因此需对不同弯曲方向分别考虑铰区长度的计算公式.
3.3铰区长度计算公式
根据板壳稳定理论[13],铰区长度Lh与截面的几何构型,包括高、宽、高宽比、板件宽厚比及其组配均有关.H形截面尺寸的定义见图3b.为得到Lh的表达式,本文建立了不同h与b组合、不同板件宽厚比组合及不同轴压比作用下H形截面悬臂钢构件在常轴压力作用下分别绕强、弱轴压弯的有限元模型,受力形式如图4a所示.取悬臂构件长度L=1 500 mm,大约为普通钢结构住宅层高的一半.h与b的取值设定见表1,bf/tf,hw/tw和n的取值见表2,其中bf为翼缘外伸宽度,hw为腹板高度,tf为翼缘厚度,tw为腹板厚度.共建立了900个构件模型,包含了工程中可能出现的大部分情况.

图6 不同构件长度的铰区长度
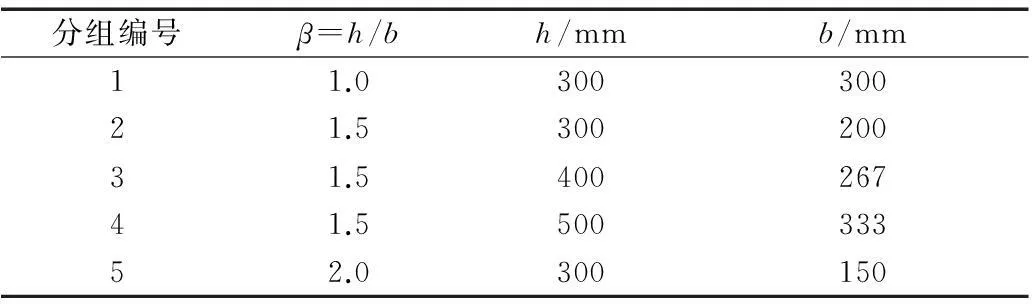
分组编号β=h/bh/mmb/mm11.030030021.530020031.540026741.550033352.0300150

表2 参数设置
从有限元分析结果中提取各模型的铰区长度Lh,将绕强轴压弯的铰区长度以Lh/h~hw/tw的形式列于图7中;将绕弱轴压弯的铰区长度以Lh/h~bf/tf的形式列于图8中.拟合回归出Lh的表达式,其中绕强轴压弯时Lh最终表达式为

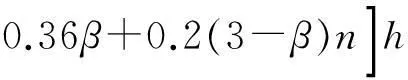
(5)
绕弱轴压弯时Lh最终表达式为
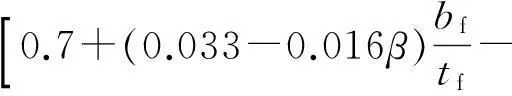

(6)
各参数分析采用式(5)和式(6)得到的计算结果用虚线分别标于图7和图8的各分图中.式(5)和式(6)得到的铰区长度与H形截面单轴压弯试验试件[8-9]的对比结果列于图9中.从图7~9可以看出,式(5)和式(6)较好地体现了Lh的变化趋势.说明拟合得到的铰区长度通过考虑不同加载条件(不同轴压比、不同弯曲方向)及不同截面构型(不同高宽比、不同板件宽厚比)的影响,能够适用于H形截面构件的模型分析.
3.4铰区长度误差分析
基于2.3节各有限元模型提取的铰区长度与式(5)和式(6)计算得到的Lh进行比较,对本文提出的铰区长度计算方法进行误差分析,分析结果见表3.表3根据Lh的主要影响因素,包括不同弯矩作用方向、截面长宽比(β=h/b)、轴压比n、腹板宽厚比hw/tw及翼缘宽厚比bf/tf,全方位体现了Lh误差的大小.
可以看到绕强轴压弯的450个有限元模型的Lh(式(5))/Lh(有限元)的平均值为1.024,标准差为0.13;绕弱轴压弯的450个有限元模型的Lh(式(6))/Lh(有限元)的平均值为1.015,标准为0.145.注意到各分项下,平均值控制在0.901~1.064之间,标准差控制在0.167以内,说明在本文的参数分析范围内,公式和误差较小,具有良好的适用性.

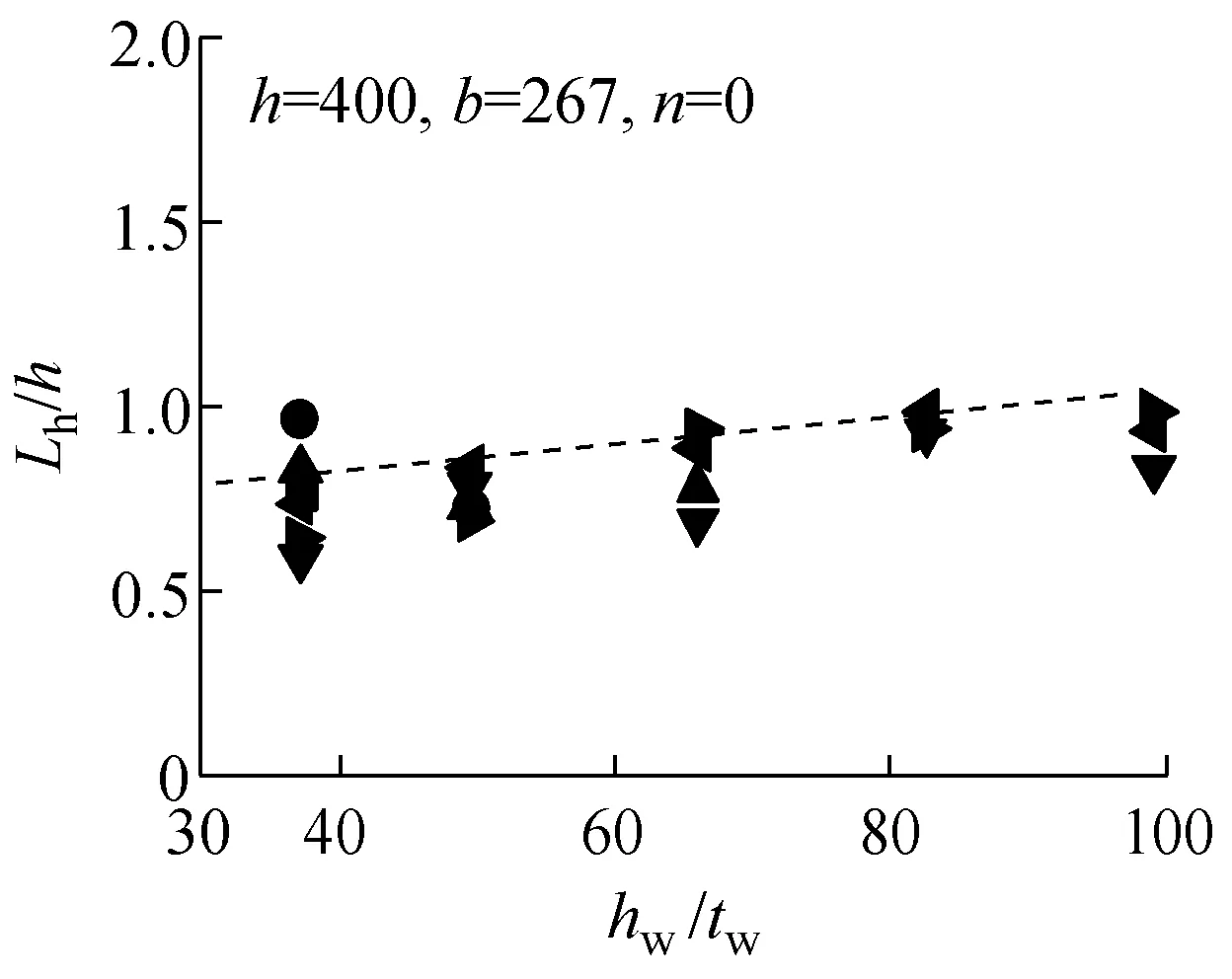

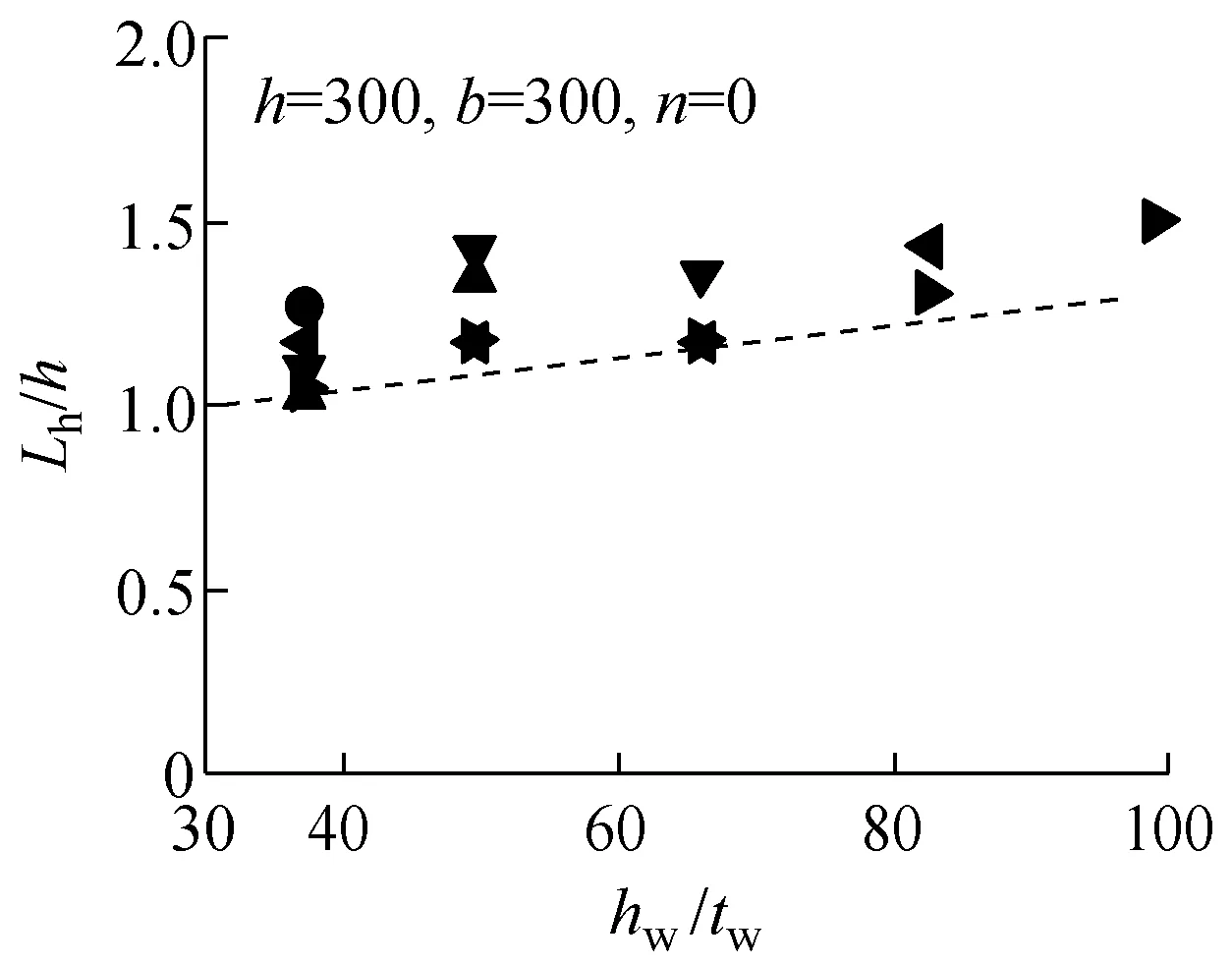
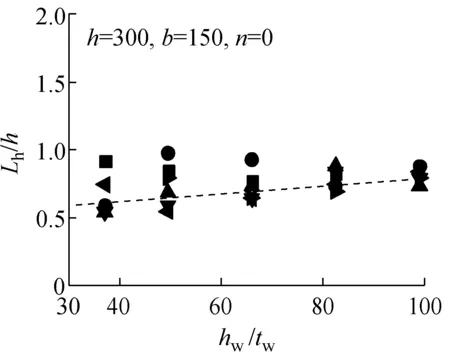








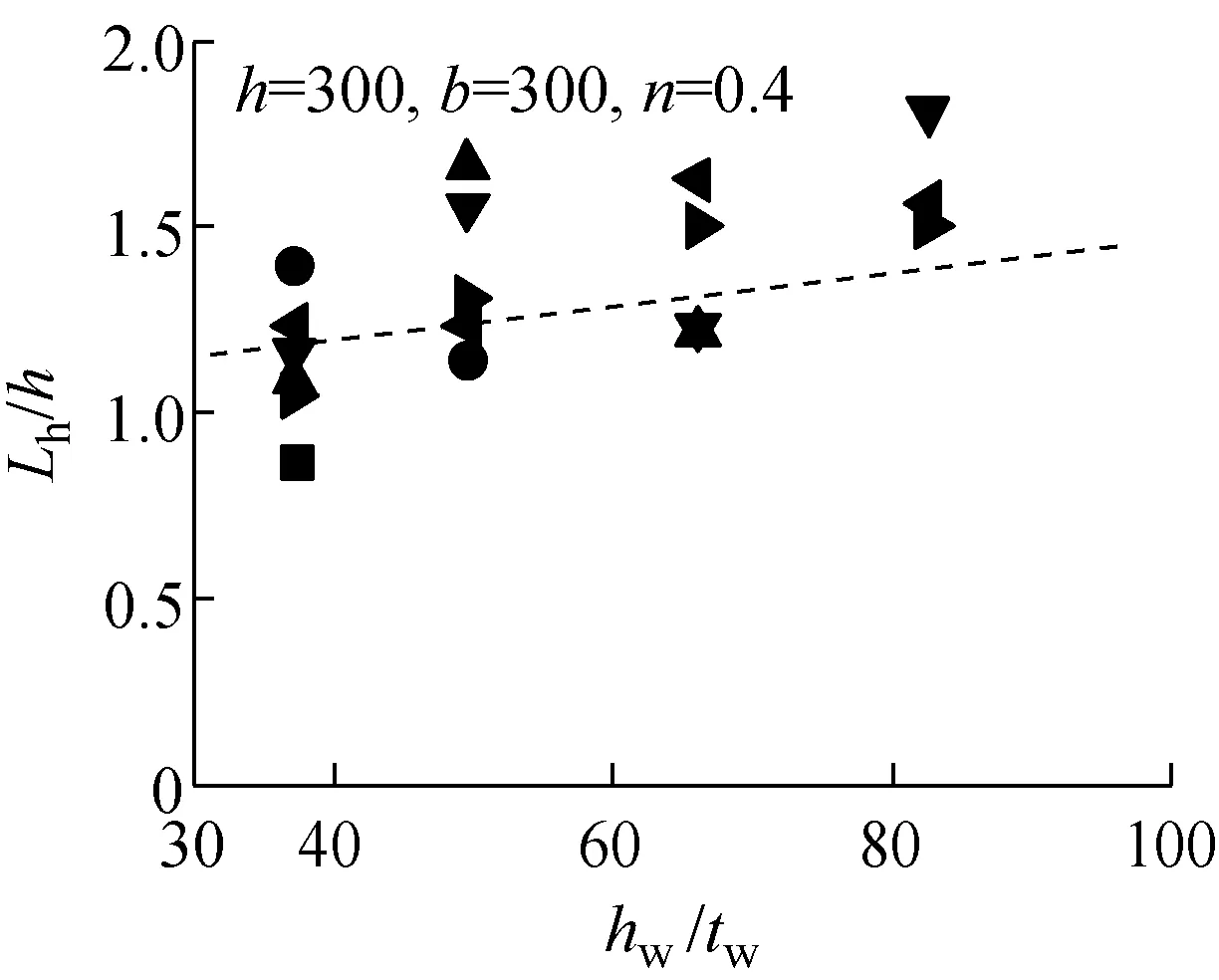
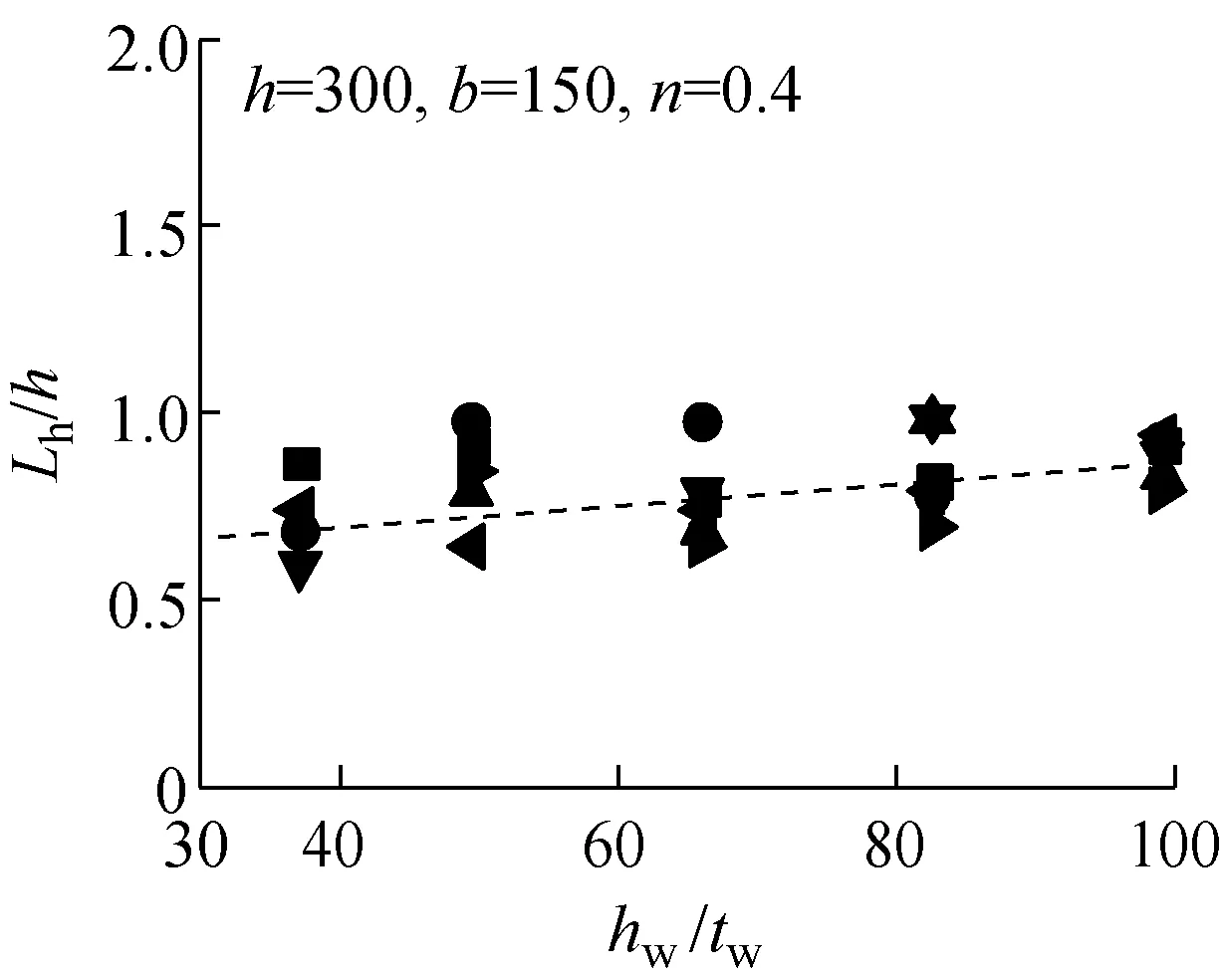

图7绕强轴各构件Lh计算结果
Fig.7Calculation results ofLhof members bent of strong axis

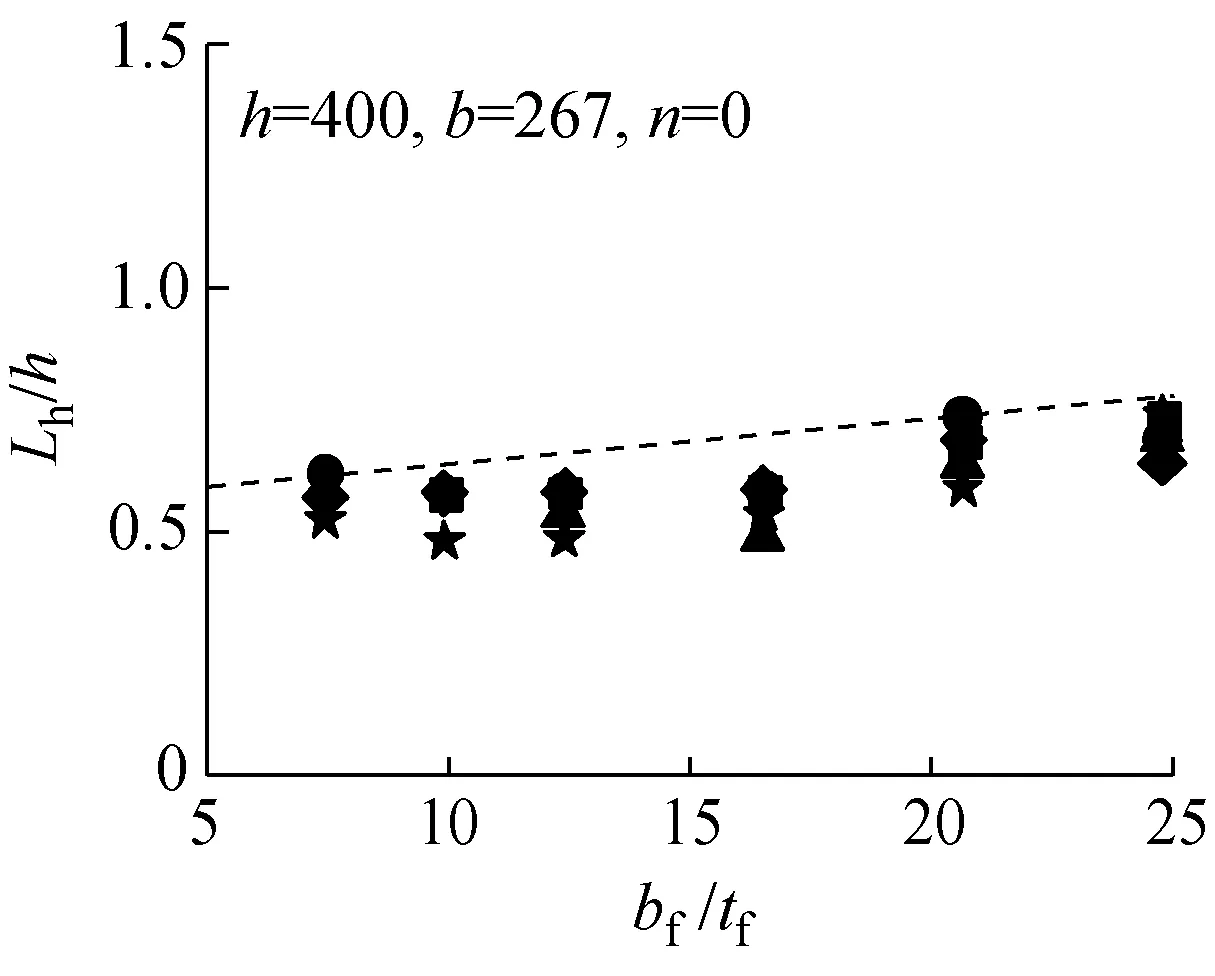


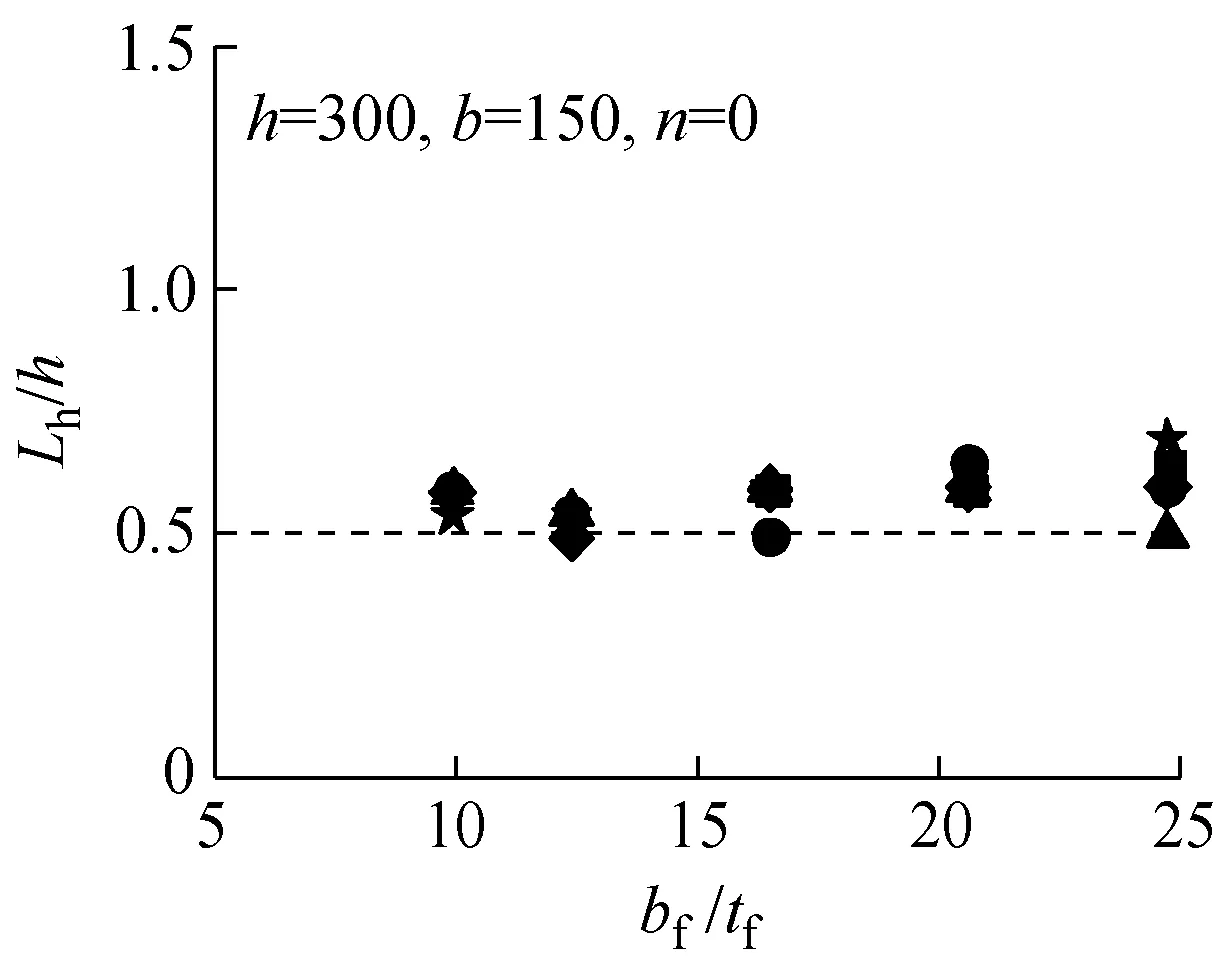

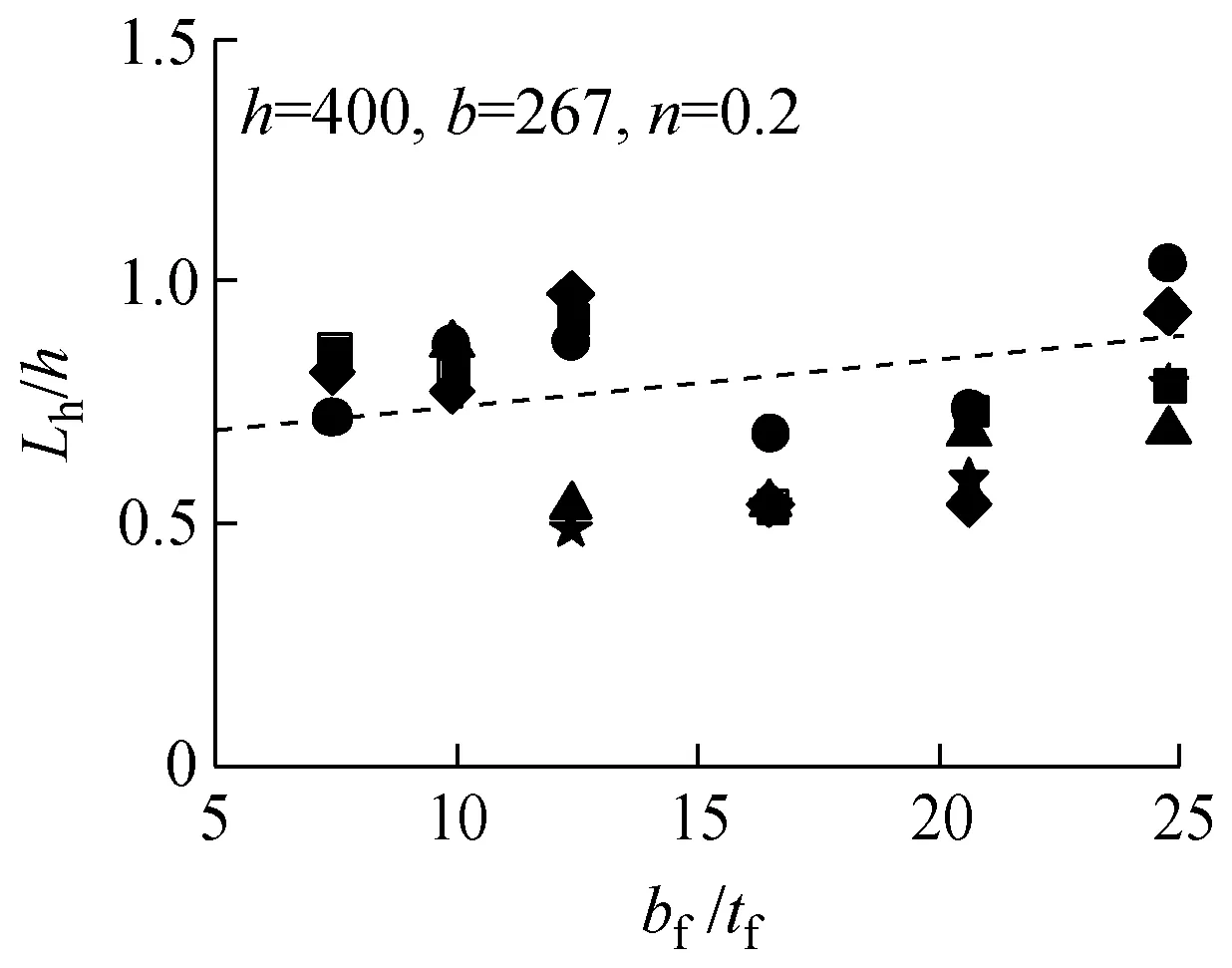





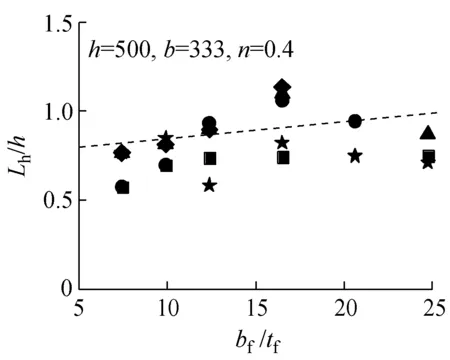
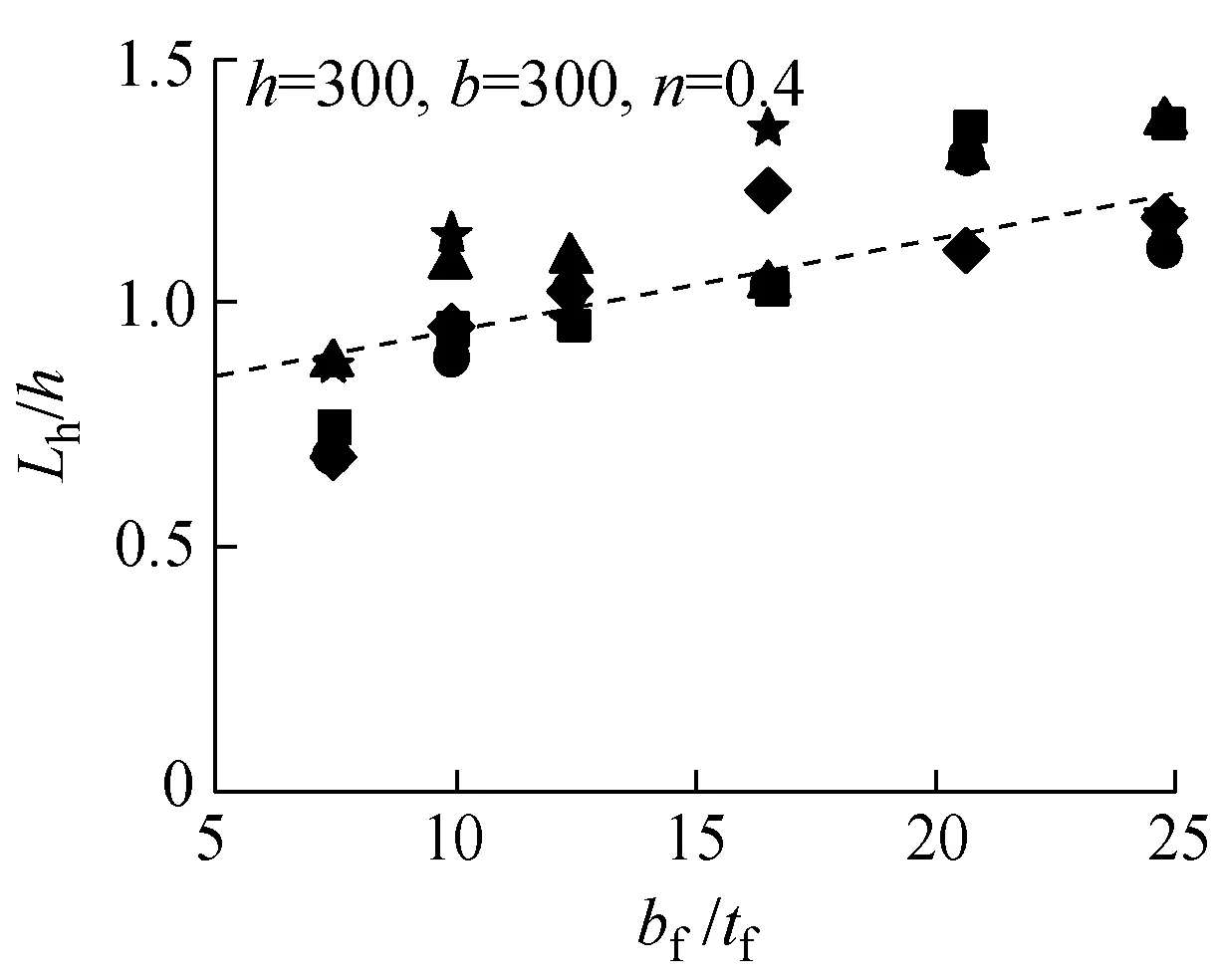


图8绕弱轴各构件Lh计算结果
Fig.8Calculation results ofLhof members bent of weak axis

图9 试验铰区计算长度与公式计算结果比较
Fig.9Comparison resluts of hinge zone length between experimental specimens and proposed equations

表3 铰区长度误差分析
4结论
本文阐述了从H形截面悬臂钢构件模型中提取扣除计算长度影响的截面层次的弯矩-曲率关系的方法,得到以下结论:
(1)铰区定义为构件局部失稳的集中区域,铰区具有一定的转动能力,有一定的长度区域,其性质可由弯矩-转角曲线进行描述.
(2)悬臂构件由铰区和弹性段组成,两部分通过一个平截面过渡,铰区的变形可从悬臂构件扣除弹性段的变形得到.
(3)拟合得到了考虑不同加载条件(不同轴压比、不同弯曲方向)及不同截面构型(不同高宽比、不同板件宽厚比)影响的H形截面铰区长度.
(4)根据本文提出的铰区模型,从构件的受力及变形结果可直接得到扣除计算长度影响的截面层次的弯矩-曲率关系.
参考文献:
[1]Nakashima M, Takanashi K, Kato H. Test of steel beam-columns subject to sidesway[J]. Journal of Structural Engineering, ASCE, 1990, 116(9):2516.
[2]Kumar S, Usami T. An evolutionary-degrading hysteretic model for thin-walled steel structures[J]. Engineering Structures, 1996, 18(7):504.
[3]Kato B. Deformation capacity of steel structures[J]. Journal of Constructional Steel Research, 1990, 17:33.
[4]Gioncu V, Petcu D. Available rotation capacity of wide-flange beams and beam-columns. 1. Theoretical approaches[J]. Journal of Constructional Steel Research, 1997, 43(1-3):161.
[5]Hasham A S, Rasmussen K J R. Section capacity of thin-walled I-section beam-columns[J]. Journal of Structural Engineering, ASCE, 1998,124(4):351.
[6]陈以一, 马越, 赵静, 等. 薄柔高频焊接H钢柱的实验和抗震承载力评价[J]. 同济大学学报:自然科学版,2006, 34(11):1421.
CHEN Yiyi, MA Yue, ZHAO Jing,etal. Tests on high-frequency welded H steel columns with slender elements and its evaluation of seismic resistance[J]. Journal of Tongji University: Natural Science, 2006, 34(11):1421.
[7]陈以一, 吴香香, 程欣. 薄柔构件钢框架的承载性能特点研究[J]. 工程力学, 2008, 25(S2):62.
CHEN Yiyi, WU Xiangxiang, CHENG Xin. Capacity and deformability of steel frames composed of members with non-compact or slender elements[J]. Engineering Mechanics, 2008, 25(S2):62.
[8]Cheng X, Chen Y Y, Pan L L. Experimental study on steel beam-columns composed of slender H-sections under cyclic bending[J]. Journal of Constructional Steel Research, 2013, 88:279.
[9]Cheng X, Chen Y Y, Nethercot D A. Experimental study on H-shaped steel beam-columns with large width-thickness ratios under cyclic bending about weak-axis[J]. Engineering Structures, 2013, 49:264.
[10]陈以一, 程欣, 贺修樟. 薄柔截面构件屈曲铰及钢框架破坏机构分析[J]. 建筑结构学报, 2014, 35(4):109.
CHEN Yiyi, CHENG Xin, HE Xiuzhang. Buckling hinge of non-plastic section members and analysis of failure mechanism of steel frames[J]. Journal of Building Structures, 2014, 35(4):109.
[11]程欣, 陈以一. 考虑板件相关作用的H形截面压弯钢构件抗弯承载力[J]. 工程力学, 2015(3):41.
CHENG Xin, CHEN Yiyi. Moment resistance of H-section steel beam-columns considering the interactive effect of plate elements[J]. Engineering Mechanics, 2015(3):41.
[12]程欣, 陈以一. H形截面钢构件绕弱轴抗弯承载力[J]. 同济大学学报:自然科学版, 2014, 42(1):31.
CHENG Xin, CHEN Yiyi. Moment resistance of H-section steel members bent about minor axis[J]. Journal of Tongji University: Natural Science, 2014, 42(1):31.
[13]吕烈武, 沈世钊, 沈祖炎, 等. 钢结构构件稳定理论[M]. 北京: 中国建筑工业出版社, 1983.
LV Liewu, SHEN Shizhao, SHEN Zuyan,etal. Stability theory of steel structures[M]. Beijing: China Architecture & Building Press, 1983.
Hinge Zone Model of H-Section Steel Members and Hinge Zone Length
CHENG Xin1, 2, CHEN Yiyi2
(1. College of Architecture and Civil Engineering, Taiyuan University of Technology, Taiyuan 030024, China; 2. State Key Laboratory of Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China)
Abstract:Characteristic properties of the hinge zone, defined as the concentration area of local buckling, were carefully investigated in this paper, based on which the calculation equation for the mean curvature of the hinge of H-sections failed by local buckling was proposed. Because the length of hinge zone is dependent on sectional configuration as well as axial force ratio, the calculation method for the hinge zone length considering the effects of sectional configuration and loading conditions was put forward by induction. Thus, the relationship of cross-sectional moment-curvature eliminating the effect of member length of H-sections according to arbitrary cantilever beam-columns was obtained. It is noted that such moment-curvature can be applied to nonlinear analysis of members with different loading conditions, lengths and boundary conditions, hence the nonlinear analysis efficiency of steel structures can be improved with satisfactory accuracy for engineering study.
Key words:beam-column; hinge zone model; mean curvature; hinge length; flexural deformation
收稿日期:2016-01-06
基金项目:国家自然科学基金(51038008, 51408394)
通讯作者:陈以一(1955—),男,教授,博士生导师,工学博士,主要研究方向为钢结构.E-mail:yiyichen@tongji.edu.cn
中图分类号:TU391
文献标志码:A
第一作者: 程欣(1986—),女,讲师,工学博士,主要研究方向为钢结构.E-mail:xcheng0309@gmail.com

