塔式起重机起重臂的有限元分析及多目标优化

许觅婷，李　纳，谢天胜

（郑州大学 力学与工程科学学，河南　郑州　450001）



塔式起重机起重臂的有限元分析及多目标优化

许觅婷，李纳，谢天胜

（郑州大学 力学与工程科学学，河南郑州450001）

摘要：文章以轻量化和稳定性为目标，建立塔式起重机起重臂的优化模型，利用ANSYS软件及MATLAB遗传算法对3种工况下的优化设计进行了分析研究，计算得到臂架重量为2912.91kg，其与规范设计重量3472.73 kg相比，减轻了16.12%，且具有更高的安全性。这对大型塔式起重机结构的轻量化和安全性设计将有重要意义。

关键词：塔式起重机；起重臂；遗传算法；有限元；稳定性

近年来，塔式起重机在建筑行业得到广泛应用，并不断向大型化方向发展，但普遍存在自重大、结构布置不合理、稳定性差， 安全性低等缺点。有限元软件的应用为塔式起重机的优化设计提供了极大便利，但其主要以轻量化为研究目标，对安全性和稳定性的研究相对较少［1］，且算法不太适用大型构件；而MATLAB遗传算法可以弥补这一不足。本文以QTZ40塔式起重机为例，应用ANSYS对结构进行分析，并结合MATLAB遗传算法优化设计，得到满足塔机轻量化和稳定性的设计参数，以期为塔式起重机起重臂的多目标优化设计提供参考依据。

1　设计数学模型

结合起重臂的结构特点，将实际问题转化为由设计变量、目标函数和约束条件构成的数学模型。其中设计变量包括各构件的截面尺寸和拉索位置；约束条件包括截面尺寸、结构强度、挠度、稳定性、布置要求等；目标函数是设计变量的函数，受状态变量的约束。

1.1模型假设

1.1.1截面假设

QTZ40塔机起重臂与拉杆视为整体，采用杆单元。拉索为弹性拉杆，且不忽略横向振动的影响。腹杆采用杆单元，上弦杆和下弦杆采用梁单元；塔帽与拉索、起重臂根部与塔身的结合处均采用节点连接，忽略起重臂沿臂长方向的横截面变化［2］。

1.1.2约束假设

拉索为杆单元，忽略起重臂与塔身铰链、塔身与塔帽的位移；起重臂根部与塔身、拉杆与塔帽之间均为固定端约束，并忽略其变形。

1.1.3载荷假设

变幅小车与下弦杆四点接触，将外载荷平均分配到小车附近4个节点上。根据圣维南和虚功原理，这样对整体结构受力情况没有影响［3］。重力处理为均布荷载。

1.2设计变量

塔式起重机起重臂结构简图如图1所示。起重臂整体由单节列阵组成，分内跨、外跨、外伸段三部分，各部分腹杆和上、下弦杆规格相同，节段数不同［4］。将臂架视为三段截面相同、长度不同、横截面为等腰三角形的空间桁架结构。拉索为截面积不同的杆单元，上弦杆为钢管，下弦杆为实心方管。

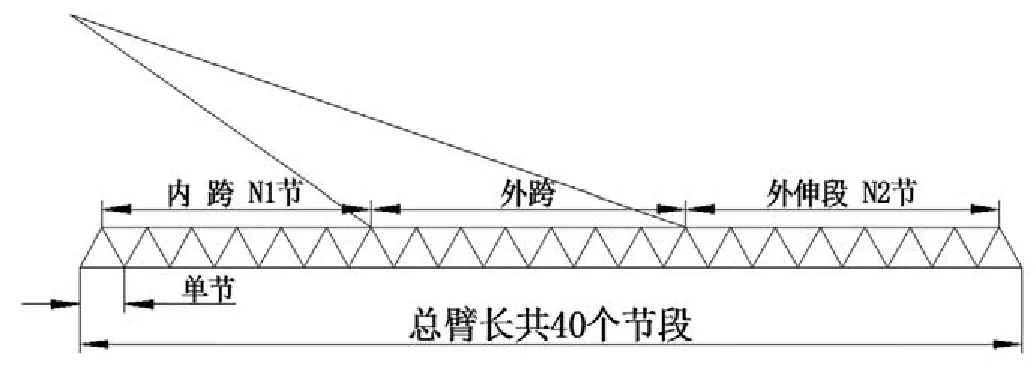
图1　起重臂结构简图

1.3设计多目标函数

以起重臂在端壁、内夸及外跨掉载3种工况下工作时臂架最轻且安全性最高为目标，对3种工况下分别加规定载荷求解。同时考虑臂架的稳定性和安全性，以起重臂自重和稳定性作为目标函数，求得各工况下的最小稳定性特征值即屈服载荷［5］。

对于多目标优化问题，实现得到的最优解同时使各分目标函数也达到最优较为困难。本文用线性加权组合法来统一目标函数［6］。首先评价各目标权重系数，然后将自重和最小稳定性特征值统一为单目标函数进行优化。另外，通过优化各杆件截面特性和几何布置来改变其强度、刚度，实现对优化目标的收敛。起重臂多目标优化数学模型表达式为：，其中为起重臂总质量，为最小稳定性特征值，，分别为自重与屈服载荷加权因子。

1.4约束方程的确定

1.4.1强度约束

1.4.2截面尺寸和几何模型约束

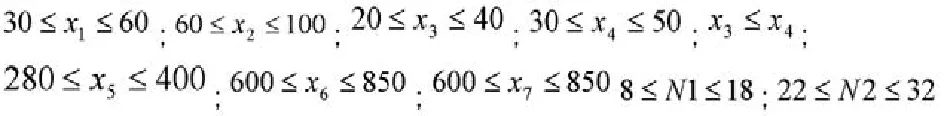
1.4.3挠度约束

2　设计优化算法

ANSYS提供常用的零阶和一阶算法。零阶算法局部搜索能力较差，难以收敛到最优解［6］；一阶算法较易收敛到局部极值点，且两者均只适用于简单问题。而遗传算法不受搜索空间的限制，同时避免仅收敛于局部最优解，在解空间启发式的搜索避免过大的工作量，可以高效、精准地解决复杂优化问题。故本文采用遗传算法，通过MATLAB调用ANSYS程序来研究遗传算法在结构优化中的应用。

3　起重臂优化设计

首先利用ANSYS对结构进行静力和稳定性分析，然后根据自重、稳定性和受力情况建立优化模型，最后利用MATLAB遗传算法工具箱进行求解。该优化方法不仅程序简单，而且可以得到较优解。

3.1 建立起重臂有限元模型

起重臂处理为桁架结构，杆之间的交汇处均作为节点。建模时，拉索单元类型为LINE10，腹杆单元类型为LINE8，采用BEAM188梁单元进行模拟。部分ANSYS命令流如下：

3.2有限元求解并输出

考虑3种工况下分别在指定位置施加规定载荷进行静力和稳定性分析，计算得到总质量、最大位移值、最大应力值和稳定性特征值，将得到的数据输出到文本文件中，供MATLAB读入数据结果。ANSYS输出数据命令流如下：

3.3MATLAB调用ANSYS

ANSYS程序提供了批处理运行方式，可以在后台运行计算并输出结果。MATLAB调用ANSYS命令流后，有限元执行命令流将结果输出到文本文件中，最后MATLAB读入结果数据进行优化设计。

3.4循环过程

利用ANSYS软件和遗传算法结构优化设计的步骤如下：（1）Matlab中产生设计变量种群。（2）检查是否满足约束条件，如果满足，则将变量值存到dam.txt的同时Matlab执行模型命令流，之后Ansys读入dam.txt中变量，结果保存在conclusion.txt中；如果不满足约束条件，则重新开始计算。（3）Matlab读入结果计算目标。（4）检查是否收敛，若收敛，则得到结果；若不收敛，则重新开始计算。

4　结果与分析

4.1优化结果

计算得到几何模型和截面模型变量设计参数：下弦杆宽度、高度优化值分别为=35.35mm，=77.93mm，上弦圆管内、外径优化值为=25.16mm，=31.53mm，腹杆、短拉索、长拉索截面积优化值为=286.10mm2，=675.64mm2，=668.04mm2，内跨及外伸段节数优化值为=12，=11。

4.2分析与讨论

利用有限元软件和遗传算法工具箱优化分析，得到的臂架较优重量为2912.91kg，与规范设计重量3472.73 kg相比， 减轻了16.12%。优化后的最大应力值和最大位移虽有一定的增加，但稳定性特征值增大，臂架的安全度更高。由此表明，利用ANSYS和MATLAB对起重臂多目标设计具有显著的优化效果。

5　结论

（1）本文建立了以总质量和稳定性为目标函数的多目标数学模型，并采用权重统一目标法对模型进行求解，得到的最优解可以同时满足轻量化和优异稳定性能的要求，对起重臂优化设计具有重要意义。

（2）结合有限元分析软件和MATLAB优化工具箱的优化设计，其编程简单、求解快速、精度高，验证了该方法对复杂、多变量和多目标问题求解的可行性，在复杂问题的求解中具有一定的推广价值。

【参考文献】

［1］王忠，许志沛，王璋，等.动臂型塔式起重机的平衡臂结构优化研究［J］.机械设计与制造，2012（9）：151-153.

［2］侯宝佳，黄琼，涂序年.动臂式塔式起重机起重臂结构优化设计［J］.建筑机械化，2011（11）：24-25.

［3］马东辉，赵东.基于ANSYS和MATLAB的结构优化设计［J］.制造业自动化，2013（10）：106-108.

［4］李新华，张毅，戴 琳.塔式起重机起重臂的模糊优化设计［J］.机械与电子，2010（9）：92-93.

［5］谷礼新，郑海斌，彭卫平，等.塔式起重机起重臂结构和稳定性有限元分析［J］.机电工程技术，2005（8）：27-28.

［6］张毅.基于ANSYS塔式起重机起重臂多目标优化设计［D］.长沙：中南林业科技大学，2010.

［7］宋宏伟，刘浩.基于MATLAB与ANSYS 的结构优化设计［J］.大连民族学院学报，2011（3）：284-287.

Finite Element Analysis and Multi-objective Optimization Design of Tower Crane Hoist Boom

Xu Miting, Li Na, Xie Tiansheng
（School of Mechanics and Engineering Science， Zhengzhou University， Zhengzhou450001， China）

Abstract：Lightweight and stability multi-objective optimization model of tower crane hoist boom is established and the optimal design under the three working condition is analyzed by ANSYS and genetic algorithm in the MATLAB. The results show that the weight of boom is equal to 2912.91kg, which decreased by 16.12% in comparison with standard weight of 3472.73kg and safety is higher. This will be important in structure design of heavy lift within lightweight and safety.

Key words：tower crane； hoist boom； genetic algorithm； the fnite element； stability

作者简介：许觅婷（1986-），女，四川自贡，硕士，助教；研究方向：先进材料与计算。