基于CUDA异构并行加速的两行根数算法的研究

冯　森

（中国矿业大学（北京），研究生院，北京　100083）



基于CUDA异构并行加速的两行根数算法的研究

冯森

（中国矿业大学（北京），研究生院，北京100083）

摘要：随着航天技术的迅速发展，宇宙中航天器越来越多，利用两行根数（TLE）的数据对航天器的位置、运行状态、运行轨道监控分析判断，防止航天器相互碰撞，显得尤为重要。如果能减少两行根数的计算时间，无疑会让监控更加实时，地面控制中心快速做出相应操作。NVIDIA的CUDA并行计算编程架构结合高性能计算显卡（GPU）正是为了解决高性能计算问题而推出的，可以大幅缩短复杂计算的时间。文章研究了两行根数算法的并行改造，利用CUDA并行架构和GPU硬件作为CPU的协处理器，将两行根数算法的计算时间大幅缩小，解决了两行根数的计算时间问题。实验结果证明利用CUDA并行加速的两行根数算法计算时间大幅减少，提高了计算效率。

关键词：两行根数；CUDA；并行计

两行根数TLE（Two-Line Element）是北美防空司令部（NORAD，NorthAmerican Air Defense Command）基于一般摄动理论生成的一组根数体系。它是由两行具有特殊意义的数字和字母组成的，用来预报地球飞行器的位置和速度，对于定位空间卫星具有很重要的作用，因此提高两行根数的运算速度有着十分重要的意义。SGP4（simplified general perturbations satellite orbit model 4）模型是由Ken Granford在1970年开发的，NO-RAD（美国北美空间防御司令部）基于SGP4算法开发了一种广泛应用于空间目标轨道预报的软件，它的输入数据是两行根数。将两行根数代入SGP4模型，即可求出任意时刻空间目标的位置和速度。1980年NO-RAD公布了针对两行根数的SGP4模型程序代码。

2007年NVIDIA 公司推出了一种通用并行计算架构CUDA，该架构使GPU能够解决复杂的计算问题。它包含了CUDA指令集架构以及GPU内部的并行计算引擎。开发人员可以使用熟悉的C，C++，FORTRAN等高级语言来编写程序。 目前CUDA被广泛应用于石油勘测、流体力学模拟、分子动力学仿真、生物计算、图像处理、音视频编解码、航天等领域，在很多应用中获得了几倍、几十倍，乃至上百倍的加速比。

本文利用CUDA并行异构方法对两行根数算法进行并行加速改造，提高卫星位置和速度信息的计算速度显得尤为必要。

1　CUDA并行加速改造原理介绍

传统的CPU计算是串行计算。串行计算由一组离散的指令序列组成，在一个CPU上指令序列被一个一个的依次运行，并且在任何时间最多只有一个指令在运行。

并行计算可使用多个计算资源解决计算问题。并行计算的模块可以被分为几个离散的部分被同时运行，每一部分包含一组指令序列在不同的处理期上同时运行。采用并行计算需要具备两个条件：拥有多个计算资源、问题可被分解为多个独立的工作块。由于同一时间有多个计算指令在运行，因此解决问题的时间比串行计算更短。CUDA架构数据处理流程如图1所示。

图1　CUDA架构数据处理流程

CUDA编程模型将CPU作为主机（Host），GPU作为协处理器或者设备（Device），它们协同工作，各司其职。CPU负责进行逻辑性强的事务处理和串行计算，GPU则专注于执行高度线程化的并行处理任务。运行在GPU上的CUDA并行计算函数称为内核函数。一个内核函数并不是一个完整的程序，而是一个可以被GPU并行执行的计算任务。CUDA的线程模型，内核以线程网格（Grid）的形式组织，每个线程网格由若干个线程快（block）组成，而每个线程块又由若干个线程（thread）组成。每个线程都有唯一的坐标，线程根据其所在的线程块的块号和块内的线程号来访问存储区及互相通信。如图2所示。

图2　CUDA线程模型

2　两行根数算法的并行加速改造

每一颗卫星的TLE轨道报的正文都是由两行构成，格式如表1所示。其中，第0行是卫星名称，第1行和第2行是标准的NORAD两行根数轨道报格式。具体的两行根数轨道参数描述如表2和表3所示。

表1　TERRA卫星TLE轨道根数参数

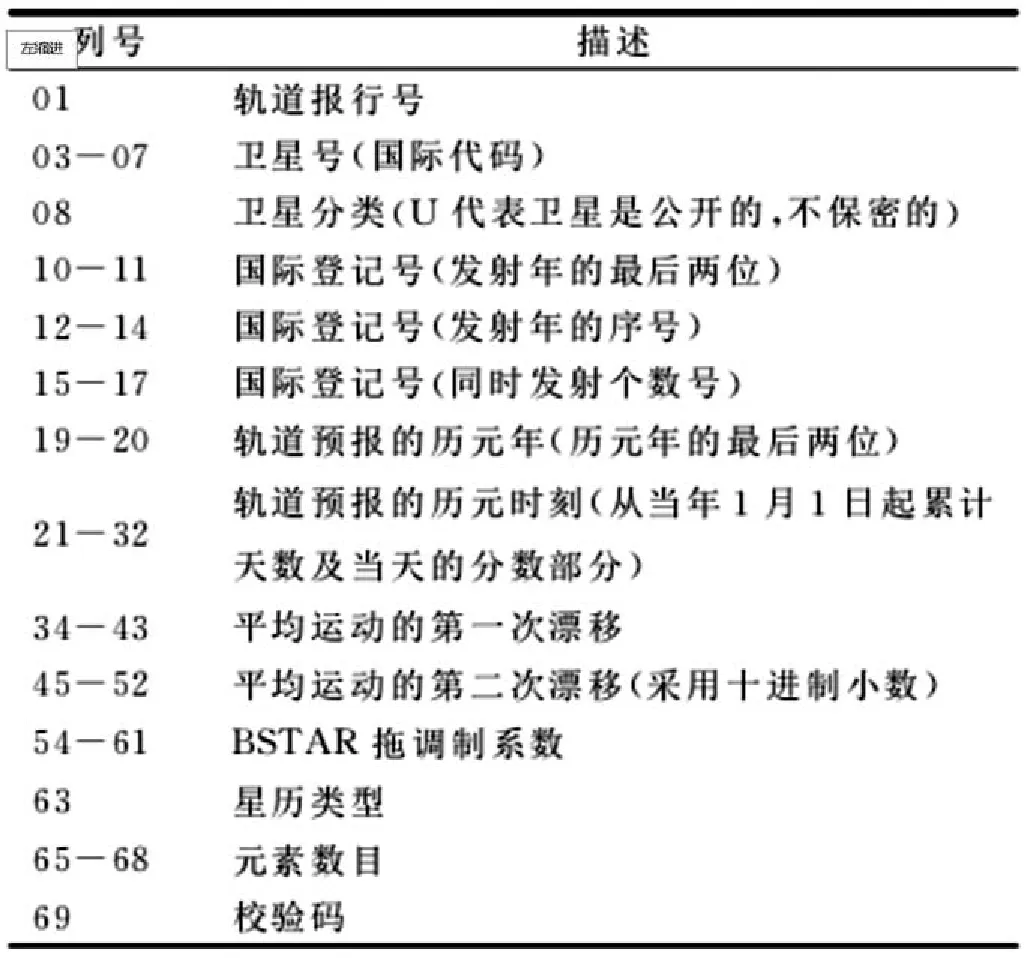
表2　TLE轨道参数第1行格式描述

表3　TLE轨道参数第2行格式描述

目前NORAD发布的 TLE计算卫星轨道的方法是采用SGP4/SDP4模型进行计算的，其算法流程如图3所示。

整个算法计算量最大的地方在于n次for循环对循环体的计算，每次SGP4/SDP4模型的计算之间数据耦合度为0，所以这个算法适合使用CUDA并行模型进行加速改造。改造的方法如下：（1）首先将CPU中两行根数的计算数据传入GPU中。（2）在GPU中启动N个线程对应并行计算N次for循环中的SGP4/SDP4模型计算处理。（3）等待所有GPU线程计算完成后，将计算结果传送给CPU，继续算出位置和速度信息的处理。（4）最终算出卫星的速度和位置。

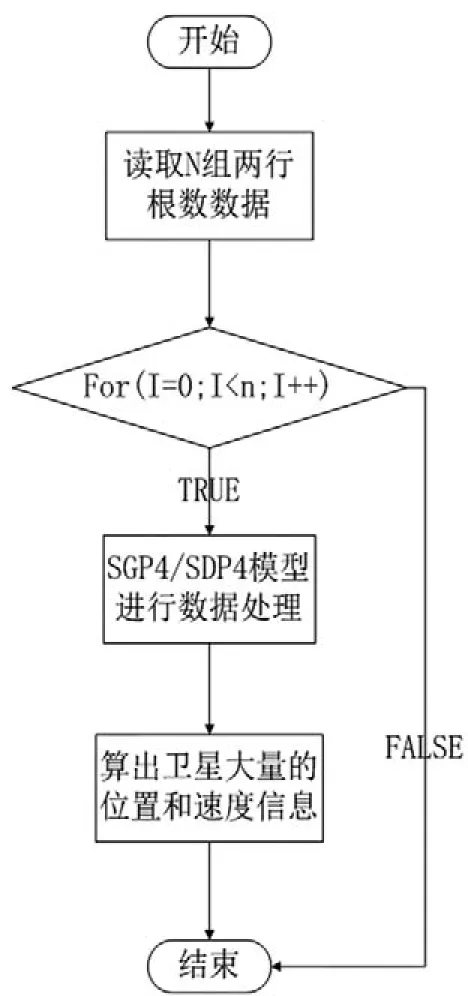
图3　SGP4/SDP4模型计算两行根数算法流程

3　实验测试结果

采用两行根数部分数据进行测试，比较使用CUDA加速前和加速后的结果如图4-5所示。由测试结果可知，使用CUDA并行加速之后的两行根数计算效率大大提高，计算时间大约缩短了1/14。

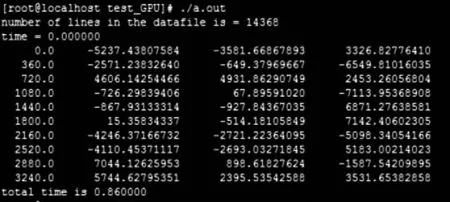
图4　CUDA并行加速改造前的计算时间

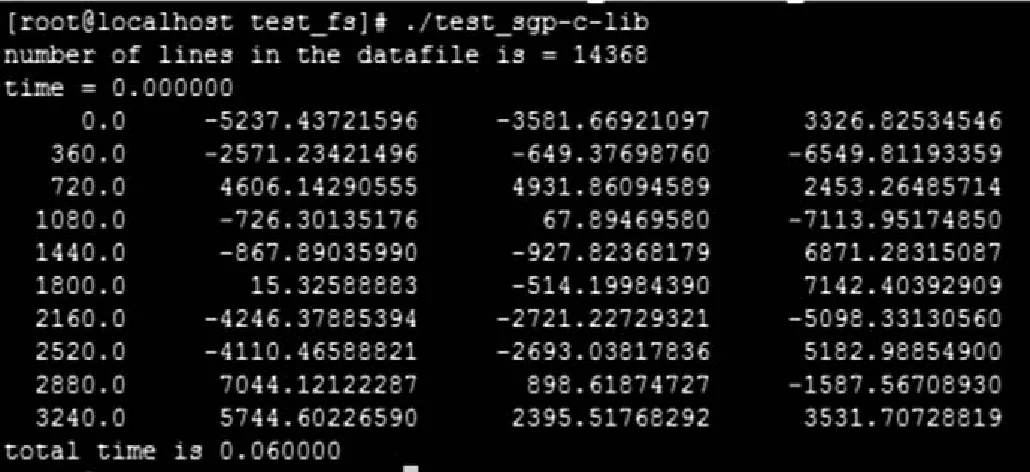
图5　CUDA并行加速改造后的计算时间

4　结语

本文通过对基于CUDA并行加速改造的两行根数算法的研究，探索了CUDA在航天领域的应用，解决了两行根数计算效率问题。并行加速改造除了使用GPU外，还可以使用CPU多进程的方法进行并行计算，再结合CUDA编程模型，算法的计算时间将会进一步缩短，这可以作为以后的一个新的研究方向。

［参考文献］

［1］KELSO TS.Two-Line Element Set Format［EB/OL］.http：//celestrak.com/columns/v04 n03/FAQ01.

［3］B.Wun，J.Buhler， and P.Crowley.Exploiting Coarse Grained Parallelism to Accelerate Prote in Motif Finding with a Network Processor［C］//PACT 2005： In Proceedings of International Conference on Parallel Architectures and Compilation Techniques，2005.

［4］Zhiyi Yang， Yating Zhu， Yong Pu.Parallel Image Processing Based on CUDA［C］//CSSE2008： proceeding of 2008 International Conference on Computer Science and SoftwareEngineering，2008.

［5］韩潮，章仁为.利用雷达测高仪的卫星自主定轨［J］.宇航学报，1999（7）：1.

［6］杨维廉.关于卫星运动的交点周期［J］.航天器工程，1997（3）：33-34.

Research on Heterogeneous Parallel CUDA Accelerated Two Lines of the Number of Algorithm

Feng Sen
（Graduate School， China University of Mining （Beijing）， Beijing100083， China）

Abstract：With Space Technology rapid development， more and more spacecraft in the universe using two lines of the number （TLE）data on the spacecraft's position， running， running track monitoring analysis and judgment to prevent aerospace collide with each other，it is particularly important. If you can reduce the number of computing time two lines， no doubt will make more real-time monitoring， the ground control center to quickly make the appropriate action. NVIDIA CUDA parallel computing architecture with high-performance computing programming graphics card （GPU） in order to solve the problem and the introduction of high-performance computing， complex calculations can signifcantly shorten the time. In this paper， the number two lines parallel transformation algorithm using CUDA parallel hardware architecture and GPU as a CPU coprocessor， will significantly reduce the number of two-line computing time algorithm to solve the problem of computing time two rows of the number. Experimental results show that the use of CUDA parallel acceleration of the number of two-line algorithm reduces computational time and improve effciency.

Key words：two lines of the number; CUDA; parallel computing

作者简介：冯森（1986-），男，辽宁沈阳。