多层网络和含时网络的相关问题研究
辜 姣,郭 龙,江 健,池丽平,李 炜
(1.江南大学理学院,江苏 无锡214122; 2.华中师范大学盖尔曼复杂性科学研究所,武汉 430079;3.中国地质大学(武汉)数学与物理学院,武汉 430074;4.武汉纺织大学非线性研究所,武汉 430200)
多层网络和含时网络的相关问题研究
辜姣1,2,郭龙3,江健4,池丽平2,李炜2
(1.江南大学理学院,江苏 无锡214122; 2.华中师范大学盖尔曼复杂性科学研究所,武汉 430079;3.中国地质大学(武汉)数学与物理学院,武汉 430074;4.武汉纺织大学非线性研究所,武汉 430200)

摘要:从多层网络的鲁棒性、多层网络的拉普拉斯谱、含时网络的时间特征、社会网络含时性和多层性对舆情演化动力学的影响4个方面,就近年来的一些活跃的研究课题作了综述。
关键词:多层网络;含时网络
0引言
在复杂系统研究中,一类主要的问题就是研究复杂网络的拓扑性质和动力学性质之间的关系。近几年来,网络研究出现了两类新的热点问题,其一就是关于多层网络的研究,涉及到各种不同网络之间的依赖与合作,比如电网与通信网络,疾病传播网络与社交网络,经济网络与金融网络等;另一类就是关于含时网络的研究,系统中个体间的相互作用属性是时间的函数,比如社交网络,疾病传播网络等。因此,在拓扑结构引入一些新的属性后,相应地网络的动力学性质也出现一些新的特征。本文从多层网络的鲁棒性、多层网络的拉普拉斯谱、含时网络的时间特征、含时网络下的舆论动力学4个方面,对近期的相关研究作了一个综述。
1相互依赖多层网络的鲁棒性分析
随着现代科技的迅猛发展,各种不同类型的复杂系统之间的联系也越来越紧密,如通信与电力系统,水和食物供应系统等等[1]。这些具有相互作用的复杂系统都可以用相互依赖网络来刻画。在相互依赖网络中,一个网络中的节点发生故障而失效会导致其他网络中依赖节点也发生故障,这样会进一步导致第一个网络中更多节点的失效,从而形成级联失效。这样网络间的相互影响给其鲁棒性分析带来了新的挑战,如何设计具有强鲁棒性的相互依赖网络系统已经成为当今网络科学的热点话题之一。
自从2010年,Buldyrev等[2]在《Nature》上发表了相互依赖网络的鲁棒性的重要论文之后,这方面的相关工作犹如雨后春笋,相继涌现。在文献[1]中,Buldyrev发现了一个重要的结论: 相互依赖网络比单一网络在随机攻击时更加脆弱,并且会出现与单一网络里二阶连续相变行为完全不同的一阶非连续相变。Parshani等[3]发现相互依赖网络的相变行为与网络间的依赖强度有关,当依赖强度减弱到某个临界值时,系统出现二阶相变,鲁棒性得到加强。Zhou D和Huang X等[4-5]分别发现网络间的聚集性和异质性会减弱系统的鲁棒性。高建喜等[6-7]理论分析了两个具有多重依赖关系的相互依赖网络的鲁棒性,还将蓄意攻击映射到随机攻击上,并建立了相关理论框架分析完全相互依赖和部分相互依赖网络的鲁棒性。董高高等[8-9]较为系统的研究了4类不同相互依赖网络的鲁棒性问题,它们分别是网络间只存在依赖边;网络间只存在连接边;网络间存在连接边和依赖边;网络间存在支持-依赖的有向连边。除此之外,Li W等[10]考虑了真实网络系统在空间地理中的情况。Morris等[11]调研了耦合空间网络中的运输过程。文献将二重相互依赖网络扩展到多重相互依赖网络即网络中的网络[12-16]。唐明等[17]还考虑了相互依赖网络上的疾病传播动力学行为。更多相关研究可以参考综述文章[18]。
与此相关的我们自己的研究中,主要着眼于相互依赖网络间的依赖强度及依赖关系对系统鲁棒性的影响,通过构建二重相互依赖无标度网络和相互依赖随机网络的理论模型,解析分析择优依赖和随机依赖对系统级联失效行为的影响,研究发现相互依赖无标度网络表现出二阶相变,其鲁棒性随依赖强度增大而加强,然而相应依赖随机网络则表现相反,并且网络间的择优依赖关系相比随机依赖关系更能提高系统的鲁棒性[19]。
2多层网络的拉普拉斯谱性质

考虑一个包含M层,每层N个节点的简单(无向、全连通、不存在自循环)多层网络,假设多层网络的每一个节点是可以标记的,其中第α层的邻接矩阵或强度矩阵可以表示为W(α)∈RN×N,对应的拉普拉斯矩阵为L(α)=S(α)-W(α),其中S(α)为对角元素为这一层网络中节点强度的对角矩阵。依次写出每一层网络的拉普拉斯矩阵,并使其为对角元素构成对角矩阵,则为只考虑层内联系,整个多层网络的拉普拉斯矩阵。定义WI∈RM×M为多层网络中节点层间的联系矩阵,其对应的拉普拉斯矩阵为LI=SI-WI。整个多层网络的拉普拉斯算子为L=LL+LI,其中,LL描述多层网络的节点层内联系的拉普拉斯算子(其对应矩阵为L(α),α=1,…,M的对角矩阵),LI描述多层网络节点层间联系的拉普拉斯算子。
多层网络的拉普拉斯谱与其网络的拓扑性质相关。在多层网络中,L算子的谱包含LI算子的谱。当M较小时,LI的本征值可以由层间联系强度决定[23],例如,当M=2时,LI的本征值为{0,2D},其中,D为层间关联的强度。当多层网络中层间为完全连接并具有相同的权重D时,LI的本征值可写为{0,MD{M-1}},M-1为本征值MD的重数。
在多层网络中,通过对每一层网络的拉普拉斯谱与层间不存在联系时的拉普拉斯谱进行比较时,可以看出此多层网络的层间关联是否紧密。例如,设Dx为多层网络中层间关联强度最大值和层内关联强度最大值的比值,若两者本征值近差别一个小量(约为γiDx,γi为节点i的层间联系强度),即Dx≪1,即多层网络层间关联较弱。当然,不论Dx如何设置,多层网络的拉普拉斯算子谱始终包含一个0的特征值,并且存在M-1个与Dx相关的特征值。

3含时网络的时间特征
含时网络主要用来刻画复杂系统中微观相互作用断续存在的情形[24]。例如,在手机通讯网络中,A和B之间的连边仅当A和B发生通话时才存在。通话结束后,A和B之间的连边也随之消失。按传统的复杂网络方法,仅在A、B之间产生一条连边已经不足以描述微观相互作用时刻变化的特点。于是,“时间”作为一个独立自由度引入到复杂网络中,称之为含时网络,用G(V,E,t)表示,其中t代表连边发生的时刻,如图1所示。相应地,含时网络的邻接矩阵为A:a(i,j,t)=1代表节点i和j在t时刻有联系;否则a(i,j,t)=0。因此,在含时网络中,每一条连边都带有时间,每一条路径都要考虑时间的先后顺序。含时网络的研究目的就在于揭示时间的引入对网络结构及传播过程的影响。

图1 含时网络示意图,代表节点
本文将着重从时间的角度简要介绍含时网络的研究现状:一是时间累计(time-aggregation)方法,侧重于探讨含时网络的结构特点。另一类是时序(time-ordering)的影响,侧重于分析时间先后顺序如何影响含时网络上的动力学过程。详细内容可参考Holme等的综述文献。
3.1时间累计方法

在时间累加的框架下,时间间隔Δt对描述含时网络的结构性质起着重要作用。时间间隔太小,每一个时间间隔内包含的节点和连边也少,无法观察到一些重要子图的形成或消失。时间间隔太大,每一个时间间隔内几乎包含了所有的节点和连边,无法观察到关键连边的出现等现象。目前大家主要选取自然时间单位作为时间间隔来研究。Krings等[25]以小时、天、星期等为时间间隔研究了手机通讯网络。池丽平等[26]以天、年为时间间隔分别研究了AutonomousSystems网络、科学家合作网的演化特征。Trajanovski等[27]则探讨了一定时间间隔下含时网络在随机删除与蓄意攻击下的鲁棒性;Ribeiro等[28]研究了时间间隔对随机行走过程的影响。
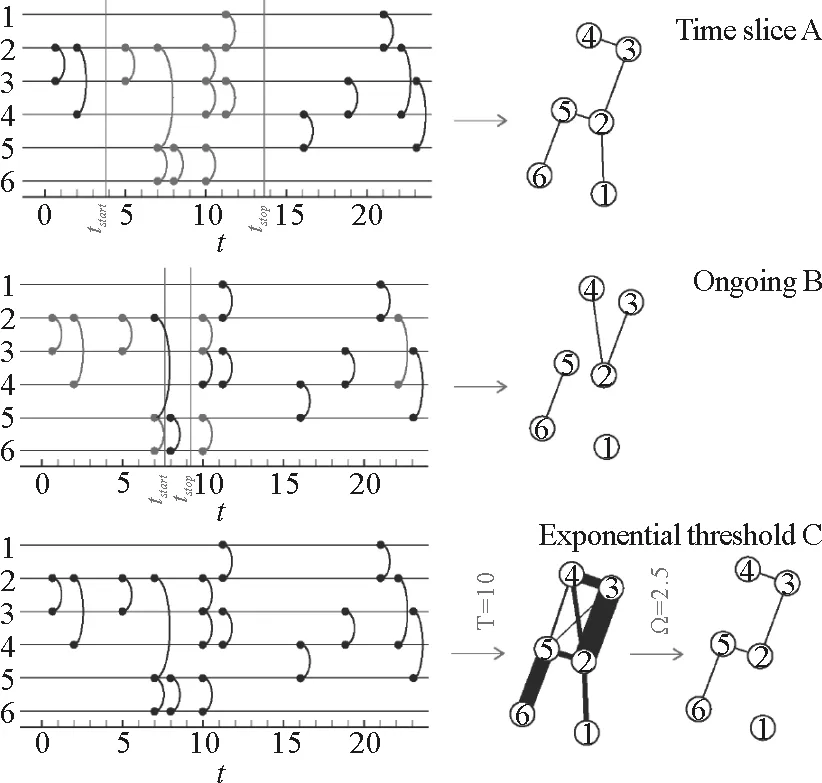
图2 将含时网络转化为静态网络的3种方法[29]
除了利用时间分段法将含时网络转化为静态网络之外,Holme还提出了另外两种方法,分别为重复出现法和指数阈值法[29],如图2所示。重复出现法是指,如果两个节点在tstart之前或tstop之后均有联系,则这两个节点之间产生一条连边。tstart与tstop的选择对静态网络的构建非常重要。指数阈值法是指,每一条连边按e-t/τ赋予权重,其中t为连边发生的时刻,τ为调节参数。如果该权重大于阈值Ω,则这条连边可以出现在静态网络中。
忽略连边的时间先后顺序,将含时网络转化为静态网络,有助于运用静态网络中一些成熟的方法来研究含时网络的结构,从而简化时间维度的分析。然而,如何选择合适的时间间隔来转化含时网络、并且最大程度地保留其时序特征,到目前为止仍是一个开放问题。
3.2时序的影响
连边存在时间先后顺序,使含时网络呈现一些特有的性质,并对含时网络上的传播过程产生重要影响。例如,可到达性是指某个时间以后,从任一节点按时间先后顺序所能到达其它节点的数目;最短时间路径定义为从节点按时间先后顺序到达节点所需的最短时间;等等。这其中最引人关注的时序特征就是阵发性。阵发性是指相继两个事件(连边)的时间间隔是不均匀的,而且多数服从幂律分布。
时序对传播过程的影响目前仍具有争议。一方面,有研究发现时间先后顺序的引入会减慢传播过程。Karsai等[30]在手机通讯数据上研究谣言传播时,发现时间序列会减慢传播速度。Starnini等[31]在研究含时网络上的随机行走时发现,时间序列同样导致传播过程减慢。另一方面,也有研究发现考虑时间序列之后会加速传播过程。Jo等[32]通过SI 模型,发现具有幂律分布的阵发性会加速传播过程。Rocha等[33]研究发现,不稳定的阵发性过程会使得SI、SIR模型的传播速度加快。与此同时,还有研究指出,时间先后顺序对传播过程的影响需要综合多种因素。Lambiotte等[34]发现阵发性幂律分布的首、尾位置对传播过程的影响不同;Holme等[35]认为传播过程与起始时间有关;Miritello[36]认为等待时间会阻碍传播,而组群对话则加速传播。
含时网络研究虽然在结构、动力学等方面取得了一定进展,然而还有很多问题亟待解决。首先,缺乏统一的理论框架来描述含时网络。比如Erdös-Rényi随机网络用参数连接概率p表示;Watts-Strogatz小世界网络由重绕概率pr决定;Barabási-Albert 无标度网络通过优先连接概率π(k)生成。然而,对于含时网络,目前还没有某个特定参量,它可以概括含时网络的时序、阵发性等特征。其次,时间间隔的影响程度还需进一步明确。怎样选择时间间隔来转化含时网络是最优的?如何衡量和评价其最优性?时间间隔内忽略了连边的时间先后顺序,必然会导致信息丢失,如何测量这些丢失的信息?最后,时间序列的重要作用还需深入探讨。时间序列为什么会影响以及怎样影响含时网络的拓扑结构和传播过程?怎样的时序斑图在网络的演化和传播中起主导作用?这些都是摆在我们面前尚未解决的问题。时间的引入使含时网络研究充满了机遇和挑战,也将有助于我们更好地认识微观相互作用时刻变化的复杂系统。
4社会网络含时性和多层性对舆情演化动力学的影响
近年来,随着互联网技术和存储技术的发展,大数据时代已拉开帷幕。人类行为痕迹被详尽记录下来,为研究人类行为动力学和社会现象的涌现机制理论研究提供了实证分析和理论验证之前期准备。这也吸引了许多物理学家对其理论量化研究的广泛关注,促进了社会物理学这一交叉领域的进一步发展[37-39]。许多物理学家利用统计物理和图论的方法和思想量化研究社会现象和社会动力学。例如:社会网络拓扑结构及其演化、语言演化、人口动力学、疾病传播动力学、舆情演化动力学等等。
舆情演化动力学是人类社会中集群动力学现象之一。舆情被认为是个体对某一感兴趣话题的判断、观点、情感和态度的表达。这种表达往往依赖于个体的主观性和客观性判断。相互影响的个体(或团体)之间舆情的趋同和分化是非常重要的社会过程[40],类似于统计物理中Ising模型中有序-无序相变。物理学中有序相对应于社会系统中个体(或团体)中舆情的一致态;而无序相对应于个体(或团体)因舆情不同而形成的群体分化现象[38]。显而易见的问题是:如何从数学或物理的角度量化分析有限尺寸大小的社会系统中的舆情演化动力学?为此,D.Stauffer和S.Solomon综述了基本的物理模型和概念,例如元胞自动机、含温度的Ising范例、逾渗理论、主方程方法[38]和平均场近似[41]。他们也展示了这些模型和概念在社会动力学中的应用,例如选举过程、金融市场和语言演化等。另外,R.Toral和C.J.Tessone概述了系统有限尺寸效应对社会动力学演化的影响,例如舆情演化的Galam模型和文化分化形成的Axelrod模型[42]。
在社会过程中,由非凡的群聚效应而导致的宏观现象多来自于社会系统中大量微观个体之间的相互作用。大量实证分析表明,社会复杂系统可抽象为社会网络,其中社会系统中的个体映射为社会网络中的节点,个体之间潜在的相互作用映射为节点之间的连边。社会网络在描述节点之间的相互作用以及作用的频度和强度等方面都表现出其特有的优越性。显而易见,社会网络的拓扑结构对舆情的演化形成起着重要的作用。前人工作中分析了一些真实社会网络的拓扑结构对舆情演化的影响,例如小世界特性、无标度特性和社团特性等[43-45]。近年来,社会网络中个体及其相互作用的多样性和含时性对舆情演化动力学的影响受到广泛关注。
社会网络中个体及其相互作用的含时性体现了社会系统中个人类行为动力学的非平庸性,例如人类活动的间歇性和爆发性,以及人类之间相互作用(例如书信往来和讯息往来)的时间间隔分布的非泊松性[55]。这对社会系统(社会网络)上的动力学行为,例如舆情的演化和形成起着重要的作用。个体之间相互作用的含时性分为两个方面,一个方面是个体间相互作用的含时性与舆情演化动力学相互耦合关联,即为诸多学者研究的自适应网络下的舆情演化动力学。自适应网络中节点间的相互作用的含时性多体现在随着节点舆情的时间演化促使节点间的连边的重绕[56]。我们曾分析了依赖舆情演化动力学下自适应社会网络上社团结构的涌现机制[57]。另一方面是个体间相互作用的含时性与舆情演化动力学无关,是社会网络中个体行为的含时性的单独体现,称为含时社会网络[58]。我们尝试分析了二维空间格子上由于人类空间行走所造成的节点间相互作用的时间特性对舆情演化动力学的影响,发现人类迁移促使舆情的传播和舆情社团的形成[59]。(注,含时网络上的舆情演化仍是一个开放问题。)
5结论
我们注意到,在多层网络和含时网络的研究中都出现了一些新的描述方法和描述手段,尽管目前并不清楚这些新的变化会不会像复杂网络最开始出现的时候带来的冲击一样迅猛。另外,对这些新的网络结构的描述目前还缺乏统一的理论和模型框架,但是这些挑战对于复杂网络甚至复杂系统的进一步发展都极为关键,解决这些问题对于理解复杂系统的多样性来说或许又是重要的一步。
参考文献:
[1]Rosato V, Issacharoff L, Tiriticco F, et al. Modelling interdependent infrastructures using interacting dynamical models[J]. International Journal of Critical Infrastructures, 2008, 4(1/2): 63-79.
[2]Buldyrev S V, Parshani R, Paul G, et al. Catastrophic cascade of failures in interdependent networks[J]. Nature, 2010, 464(7291): 1025-1028.
[3]Parshani R, Buldyrev S V, Havlin S. Interdependent networks: Reducing the coupling strength leads to a change from a first to second order percolation transition[J]. Physical review letters, 2010, 105(4): 048701.
[4]Zhou D, Stanley H E, D’Agostino G, et al. Assortativity decreases the robustness of interdependent networks[J]. Physical Review E, 2012, 86(6): 066103.
[5]Huang X, Shao S, Wang H, et al. The robustness of interdependent clustered networks[J]. Europhys Lett, 2013, 101(1): 18002.
[6]Shao J, Buldyrev S, Havlin S, et al. Cascade of failures in coupled network systems with multiple support-dependence relations[J]. Physical Review E, 2011,83(3):036116.
[7]Dong G, Gao J, Tian L, et al. Percolation of partially interdependent networks under targeted attack[J]. Physical Review E, 2012, 85(1): 016112.
[8]Dong G, Tian L, Du R, et al. Analysis of percolation behaviors of clustered networks with partial support-dependence relations[J]. Physica A, 2014, 394: 370-378.
[9]Dong G G, Tian L X, Zhou D, et al. Robustness of n interdependent networks with partial support-dependence relationship[J]. Europhys Lett, 2013, 102: 68004.
[10] Li W, Bashan A, Buldyrev S V, et al. Cascading failures in interdependent lattice networks: The critical role of the length of dependency links[J]. Physical review letters, 2012, 108(22): 228702.
[11] Morris R G, Barthelemy M. Transport on coupled spatial networks[J]. Physical review letters, 2012, 109(12): 128703.
[12] Gao J, Buldyrev S V, Havlin S, et al. Robustness of a network of networks[J]. Physical Review Letters, 2011, 107(19): 195701.
[13] Gao J, Buldyrev S V, Stanley H E, et al. Percolation of a general network of networks[J]. Physical Review E, 2013, 88(6): 062816.
[14] Dong G, Gao J, Du R, et al. Robustness of network of networks under targeted attack[J]. Physical Review E, 2013, 87(5): 052804.
[15] Cellai D, López E, Zhou J, et al. Percolation in multiplex networks with overlap[J]. Physical Review E, 2013, 88(5): 052811.
[16] Gao J, Buldyrev S V, Havlin S, et al. Robustness of a network formed by n interdependent networks with a one-to-one correspondence of dependent nodes[J]. Physical Review E, 2012, 85(6): 066134.
[17] Tang M, Cui A X, Gong K. On spreading dynamics on coupled networks[J].Complex systems and complexity science, 2011, 8(2):89-91.
[18] Li G Y, Cheng B S, Zhang P, et al. Review of the interdependent networks[J]. Journal of University of Electronic Science and Technology of China, 2013, 42(1): 23-28.
[19] Jiang J, Li W, Cai X. The effect of interdependence on the percolation of interdependent networks[J]. Physica A: Statistical Mechanics and its Applications, 2014, 410: 573-581.
[20] Pecora L M, Carroll T L. Master stability functions for synchronized coupled systems[J]. Physical Review Letters, 1998, 80(10): 2109.
[21] Almendral J A, Díaz-Guilera A. Dynamical and spectral properties of complex networks[J]. New Journal of Physics, 2007, 9(6): 187.
[22] Barahona M, Pecora L M. Synchronization in small-world systems[J]. Physical review letters, 2002, 89(5): 054101.
[23] Sole-Ribalta A, De Domenico M, Kouvaris N E, et al. Spectral properties of the Laplacian of multiplex networks[J]. Physical Review E, 2013, 88(3): 032807.
[24] Holme P, Saramäki J. Temporal networks[J]. Physics reports, 2012, 519(3): 97-125.
[25] Krings G, Karsai M, Bernhardsson S, et al. Effects of time window size and placement on the structure of an aggregated communication network[J]. EPJ Data Science, 2012, 1(4): 1-16.
[26] Chi L. Measuring microscopic evolution processes of complex networks based on empirical data[J]. Journal of Physics: Conference Series, 2015, 604(1): 012004.
[27] Trajanovski S, Scellato S, Leontiadis I. Error and attack vulnerability of temporal networks[J]. Physical Review E, 2012, 85(6): 066105.
[28] Ribeiro B, Perra N, Baronchelli A. Quantifying the effect of temporal resolution on time-varying networks[J]. Scientific reports, 2012, 3(10):3006.
[29] Holme P. Epidemiologically optimal static networks from temporal network data[J]. PLoS Comput Biol, 2013, 9(7): e1003142.
[30] Karsai M, Kivelä M, Pan R K, et al. Small but slow world: how network topology and burstiness slow down spreading[J]. Physical Review E, 2011, 83(2): 025102.
[31] Starnini M, Baronchelli A, Barrat A, et al. Random walks on temporal networks[J]. Physical Review E, 2012, 85(5): 056115.
[32] Jo H H, Perotti J I, Kaski K, et al. Analytically solvable model of spreading dynamics with non-Poissonianprocesses[J]. Physical Review X, 2014, 4(1): 011041.
[33] Rocha L E C, Liljeros F, Holme P. Simulated epidemics in an empirical spatiotemporal network of 50,185 sexual contacts[J]. PLoS Comput Biol, 2011, 7(3): e1001109.
[34] Lambiotte R, Tabourier L, Delvenne J C. Burstiness and spreading on temporal networks[J]. The European Physical Journal B, 2013, 86(7): 1-4.
[35] Holme P, Liljeros F. Birth and death of links control disease spreading in empirical contact networks[J]. Scientific Reports, 2014, 4(6186):934.
[36] Miritello G, Moro E, Lara R. Dynamical strength of social ties in information spreading[J]. Physical Review E, 2011, 83(4): 045102.
[37] Galam S. Sociophysics: a review of Galammodels[J]. International Journal of Modern Physics C, 2008, 19(3): 409-440.
[38] Castellano C, Fortunato S, Loreto V. Statistical physics of social dynamics[J]. Reviews of modern physics, 2009, 81(2): 591.
[39] Lallouache M, Chakrabarti A S, Chakraborti A, et al. Opinion formation in kinetic exchange models: Spontaneous symmetry-breaking transition[J]. Physical Review E, 2010, 82(5): 056112.
[40] Gandica Y, del Castillo-Mussot M, Vázquez G J, et al. Continuous opinion model in small-world directed networks[J]. Physica A: Statistical Mechanics and its Applications, 2010, 389(24): 5864-5870.
[41] Stauffer D, Solomon S. Applications of physics and mathematics to social science[J]. Journal of Applied Physics,2008,9(2):67.
[42] Toral R, Tessone C J. Finite size effects in the dynamics of opinion formation[J]. Communications in Computational Physics,2007,2(2):177-195.
[43] Albert R, Barabási A L. Statistical mechanics of complex networks[J]. Reviews of modern physics, 2002, 74(1): 47.
[44] Newman M E J. The structure and function of complex networks[J]. SIAM review, 2003, 45(2): 167-256.
[45] Boccaletti S, Latora V, Moreno Y, et al. Complex networks: structure and dynamics[J]. Physics Reports, 2006, 424(4): 175-308.
[46] Jalili M. Social power and opinion formation in complex networks[J]. Physica A: Statistical Mechanics and its Applications, 2013, 392(4): 959-966.
[47] Guo L, Gu J, Luo Z. How much information is needed to be the majority during the binary-state opinion formation?[J]. Physica A: Statistical Mechanics and its Applications, 2013, 392(19): 4373-4379.
[48] Guo L, Cai X. Continuous opinion dynamics in complex networks[J]. Com Computational Physics, 2009, 5: 1045-1053.
[49] Yang H X, Wu Z X, Zhou C, et al. Effects of social diversity on the emergence of global consensus in opiniondynamics[J]. Physical Review E, 2009, 80(4): 046108.
[50] Yang H X, Wang B H. Effects of social diversity on the evolutionary game and opiniondynamics[J]. Physics Procedia, 2010, 3(5): 1859-1865.
[51] Kandiah V, Shepelyansky D L. PageRank model of opinion formation on social networks[J]. Physica A: Statistical Mechanics and its Applications, 2012, 391(22): 5779-5793.
[52] Murase Y, Török J, Jo H H, et al. Multilayer weighted social network model[J]. Physical Review E, 2014, 90(5): 052810.
[53] Guan J Y, Wu Z X, Wang Y H. Effects of inhomogeneous influence of individuals on an order-disorder transition in opiniondynamics[J]. Physical Review E, 2007, 76(4): 042102.
[54] Boccaletti S, Bianconi G, Criado R, et al. The structure and dynamics of multilayer networks[J]. Physics Reports, 2014, 544(1): 1-122.
[55] Zhou T, Han X, Yan X, et al. Statisitcal mechanics on temporal and spatial activities of human (in Chinese)[J].Journal of University of Electronic Science and Technology of China,2013, 42: 481.
[56] Kozma B, Barrat A. Consensus formation on adaptive networks[J]. Physical Review E, 2008, 77(1): 016102.
[57] Guo L, Cai X. Emergence of community structure in the adaptive social networks[J]. Communications in Computational Physics, 2010, 8(4): 835.
[58] Moinet A, Starnini M, Pastor-Satorras R. Burstiness and aging in social temporal networks[J]. Physical review letters, 2015, 114(10): 108701.
[59] Guo L, Cheng Y, Luo Z. Opinion dynamics with the contrarian deterministic effect and human mobility on lattice[J]. Complexity, 2015, 20(5): 43-49.
(责任编辑耿金花)
Recent Progress on Multiplayer and Temporal Networks
GU Jiao1,2, GUO Long3, JIANG Jian4, CHI Liping2, LI Wei2
(1.School of Science, Jiangnan University, Wuxi 214122, China;2.College of Physical Science and Technology, Huazhong Normal University, Wuhan 430079, China;3.School of Mathematics and Physics, China University of Geosciences (Wuhan), Wuhan 430074, China;4.Research Center of Nonlinear Science and College of Mathematics and Computer Science,Wuhan Textile University, Wuhan 430200, China)
Abstract:In this article, a review on recent progress of related fields is given, based on the robustness of multilayer networks, the Laplacian spectra of multilayer networks, the time pattern of temporal networks, the opinion dynamics on multilayer networks and temporal networks.
Key words:multilayer networks; temporal networks
文章编号:16723813(2016)01005807;
DOI:10.13306/j.1672-3813.2016.01.004
收稿日期:2015-07-09
基金项目:高等学校学科创新引智计划(B08033),国家自然科学基金青年项目(11405118)
作者简介:辜姣(1983-),女,湖北黄石人,博士,主要研究方向为复杂网络谱图分析。通讯作者:郭龙(1982-),男,河南开封人,博士,副教授,主要研究方向为统计物理及复杂网络动力学。
中图分类号:O41; O23
文献标识码:A

