多层耦合网络传播综述
刘权辉, 王 伟, 唐 明
(电子科技大学互联网科学中心, 成都 611731)
多层耦合网络传播综述
刘权辉, 王伟, 唐明
(电子科技大学互联网科学中心, 成都 611731)

摘要:简要介绍多层耦合网络上传播动力学方面的阶段性研究进展以及存在的一些问题,主要关注的内容:多层耦合网络上的生物传播、社会传播、生物-社会耦合传播及多层耦合网络面临的一些挑战性问题。这些阶段性的研究成果从多层耦合网络的新角度加深了我们对真实传播过程及其机制的理解。能更好地控制疾病传播和减少它对人类的危害,深入探讨相关问题将有助于明确下进一步研究的方向。
关键词:网络科学;多层耦合网络;传播动力学
0引言
自网络科学理论诞生以来,传播动力学是国内外主要关注的一个课题。它可以分为生物传播[1-6]和社会传播[7-12],这两种动力学过程均是通过复制过程的方式传播。在上述两种动力学过程中,如果每个个体平均能感染一个以上的个体,那么疾病将爆发。生物传播可以抽象为一个网络上病毒的感染过程,每次接触导致感染成功的概率与之前的接触无关,是一种简单的传播过程,如计算机病毒的传播过程[2]。社会传播可以描述社会创新[7]、宗教教义[8]、健康行为[9]、谣言[13]等社会行为或消息在人类社会网络中的扩散过程。区别于生物传播,社会传播中的记忆性[11-12]、加强效应[14]等特性导致每次传播成功的概率与之前的接触相关,从而是一种复杂传播。
生物、社会两种传播过程广泛存在于自然和人类社会中,对整个人类社会造成了不同程度的影响。如在生物传播中,黑死病[15]在14世纪中叶肆虐了整个欧洲;12年前的SARS[16]突如其来,曾令整个中国措手不及;2009年3至4月在墨西哥爆发的H1N1[17]疫潮,导致过百人感染而后传播到全世界,紧接着,世界卫生组织把全球流感大流行警告级别提高到第五级;又如最近埃博拉病毒[18]在西非的再次爆发,至少已造成上万人的死亡等等。面对生物疾病给人类造成如此大的威胁,来自不同学科的专家和学者都致力于研究生物疾病的各种传播机制。如在描述艾滋病和埃博拉病毒这类突然且尚缺有效治疗手段的流行病时,学者建立了易感态-感染态(SI)传播模型[1];对于水痘和麻疹这类患者能完全康复并获得终身免疫力的流行病采用易感态-感染态-恢复态(SIR)传播模型[6];用易感态-感染态-易感态(SIS)模型来描述季节性感冒和淋病这类即使健康患者仍可能再次被感染的传染病[2]等等。社会传播主要探究社会基质(创新、行为、谣言等)等传播过程对人们正常生活中意见决策、行为采纳等影响。如2011年日本东海岸的地震发生的核泄露事故,因其中一个网友发出“日本核电爆炸对山东海域有影响,并不断地污染”等消息,而在中国产生了一场一定范围内的核辐射恐慌和抢盐事件。再如2014年的马航事件短时间内就引起了全球范围内的关注等等。为了防止社会传播中这种类似于谣言的社会基质的传播对人类正常生活的冲击,以及更大化地促进社会创新、健康行为等有益于人类社会的传播过程,学者同样建立了类似于生物传播的模型来对社会传播过程进行描述。例如在刻画个体的意见决策中,Granovetter提出线性阈值模型(LTM)来描述社会传播中群体意见的形成过程[11]。Watts提出的确定性阈值模型则可被用来描述网络结构对信息扩散的影响[12]等。在描述谣言传播过程时,Daley和Kendall建立了无知态-散布态-阻止态谣言传播模型[13]。
十几年来,国内外在单个网络上的传播动力学研究成果斐然[19]。生物传播主要从网络结构的不同尺度出发,研究宏观结构(如度分布异质性[2,20])、中尺度结构(社区[21-22])、微观角度(节点度[23],边[5,24-25])等不同网络拓扑特性对生物传播速度[26-27]、传播可预测性[3]、最终感染范围[5]和爆发阈值[6,28-30]的影响,并确定影响传播的关键环节[31-35],进一步还原疾病传播路径,寻找疾病传播源[36-37]等。研究影响疾病传播机制和网络拓扑特性的最终目的是为了更好地控制疾病传播,减少疾病传播对人类造成的危害。不同的免疫策略如目标免疫[38-41]、熟人免疫[42]、基于信息驱动的免疫[43]以及自适应策略[44]等被提出用来控制疾病的传播。社会传播在单个网络上的传播过程研究中,主要从网络的拓扑结构(比如聚集系数[45-46])、初始种子的比例和选取策略[47-48]、网络中节点的阈值分布[12,49-50]、时序网络[51]等角度出发分析它们对社会传播的阈值以及最终的传播范围的影响。Wang等还考虑个体记忆的非冗余特性对行为采纳的影响[10],发现个体的记忆特性显著地影响最终的采纳比例。在传统的传播动力学中,学者主要单独地研究上述其中一种动力学过程,而在实际生活中,上述两种动力学过程是相互交织且非对称影响。比如疾病是否会大规模的爆发取决于关于疾病的消息是否传播开来等。学者纷纷从不同角度如疾病意识的扩散[52-53]、基于局部信息的行为反应[54-55]等来研究社会传播对生物传播的影响等。
目前,已有大量关于传播动力学课题的研究,但这些研究主要集中在基于单个网络上的研究。而事实上单个网络仅仅是更大复杂系统中的一个子集,复杂系统是由许多具有不同结构与功能的多个网络耦合而成的[56-57]。在多层耦合网络中,各层的节点具有截然不同的属性,并且层与层的节点之间存在耦合作用,如在电力网络与通信网络构成的双层多层耦合网络中,通信网络依赖于电力网络的持续供电得以正常运行,电力网络中节点间的正常通讯依赖于通信网络提供的通讯渠道,二者间形成相互依存的关系[58-59]。铁路网和航空网构成的双层多层耦合网络中,层间的相互协作保障了人们旅行方便快捷[60]。通讯网络和社会接触网络组成的双层耦合网络中,它们在结构上存在相互依存关系的同时,还在信息传递过程中存在相互促进的作用[61-62]等。
近几年来,多层耦合网络上的传播动力学研究逐渐受到越来越多的关注。类同于单一网络上传播动力学的研究,学者们在多层耦合网络上研究传播过程是为了更准确地描述真实的传播过程,以便能够预测、控制传播,最终达到造福于人类的目的。以往在单一网络上传播动力学的研究中,不可避免地忽略了很多影响传播的因素,比如传播途径的多渠道性,如生物传播中基于人类出行方式(飞机、火车等)而导致疾病的多渠道传播,社会传播中基于不同交互平台[63](Facebook, Twitter, etc)、交互方式(短信,电话等)而导致信息的多路径传播等;再如两种或两种以上的传播动力学分别在不同网络上相互交织地影响传播过程,如消息在通讯网络上传播和疾病在接触网络上传播构成的非对称耦合传播[51-52]等。早期关于单一网络上的传播动力学研究,对多层耦合网络上可能发生的传播动力学过程很难进行解释。多层耦合网络上的传播动力学研究是复杂网络研究中一个崭新的领域,多层耦合网络这种全新的网络结构对于已有的传播动力学模型,比如生物传播中的SI, SIS, SIR以及社会传播中的阈值模型[11-12]是怎么影响的,以及对于传播动力学中的参量比如稳态、爆发阈值等有什么影响是一个非常值得探索的课题。此外,相比于单个网络,由于多层耦合网络结构的复杂性,其中的动力学行为将会更加丰富多彩。单个网络上的动力学行为必定会影响其它层网络,与此同时,其它层网络的变化也将反作用于这个网络,产生交互影响。
本文主要关注于多层耦合网络上的传播问题,而关于多层耦合网络上的其它动力学过程,比如级联失效[51-52,64-65]、博弈[66-67]、同步[68-70]等,在此不详细介绍,感兴趣的学者请参考相关文献。
1多层耦合网络上生物传播
实际生活中,疾病往往有多种传播路径。如性病不仅可以在由同性构成的接触网络上传播,还能在异性构成的接触网络上传播,并且由于双性人的存在,导致这两个网络并不是完全孤立的,而形成了多层耦合网络。Saumell-Mendiola等较早在多层耦合网络上研究生物传播,他们在这种全新的网络背景下研究了经典的SIS疾病传播模型[71]来揭示多层耦合网络对已有传播模型的影响。他们发现对于多层耦合网络上的SIS传播模型,少许耦合边的存在可能导致在单个网络上不存在流行病却在多层耦合网络上存在。他们还发现层间度-度关联强度会进一步减少流行病爆发阈值。几乎同时,Dickison等[72]研究了多层耦合网络上的SIR流行病传播,他们发现强多层耦合网络(即层间连边数量较多)上传播,高于传播阈值子网都会存在流行病,低于爆发阈值子网都不存在流行病;而在弱多层耦合网络(即层间连边数量较少)中,低于爆发阈值却存在混合相变,即流行病只在一个子网中存在。Wang和Li等研究了不同类型网络间的耦合,比如Erdös-Rényi(ER)网络之间的耦合、ER网络与无标度网络间的耦合等对疾病爆发阈值的影响[73],他们发现两个孤立网络构成的多层耦合网络的最大特征值与两个孤立网络的主特征向量对应的乘积相关。Buono等考虑这样一类场景,一个由两层网络构成的耦合系统,这两个网络上的节点并不完全相同,只有q比例节点相同,他们研究相同节点比例q对疾病爆发阈值的影响[74],发现当q趋近于0时,整个系统的爆发阈值约为两个孤立网络中对应的较小阈值。Zhao等研究了多层耦合网络上的免疫策略[75],他们提出了两种免疫策略,基于多层耦合网络上点的随机(目标)免疫以及基于每层节点的随机(目标)免疫,并发现对于由ER网络和ER网络构成的多层耦合网络,上述两种随机免疫策略均能有效地控制疾病,而对于由无标度网络和无标度网络构成的多层耦合网络,目标免疫效果更优等。
对于多层耦合网络上传播动力学的进一步扩展,Xu等研究多层耦合网络结构在传播过程中的相对重要性对疾病传播的影响[76-77]。他们考虑这类情形,在生病期间,个体会在家养病,导致他们会更多的与家人接触,同时减少了他们与同事、朋友之间的接触概率。鉴于此类情景,他们考虑两个网络A和B。网络A的关系的重要性为w0,网络B的关系重要性为w1,其中w1>w0。为便于分析,他们假设整个系统中有p比例边的重要性为w1,其余1-p比例节点重要性为w0。对于传播模型,采用基于接触过程的SIS模型。每个感染态(I)节点按照权重
(1)

不同的形状表示在不同的参数下的值,实线表示对应的理论值。
偏好选择一条边,以概率λ感染易感态(S)节点。Xu和Wang等首先利用平均场理论来分析关系重要性为w1的边的比例p对传播的影响,发现最终处于感染态节点的比例ρ(p)并不是单调变化的,而是存在一个p区间(pL,pR)(如图1中黑色曲线所示)。当p在区间(pL,pR)内时,整个系统中不存在流行病;当p
2多层耦合网络上的社会传播
现实生活中,比如个体在选择购买某种商品,采纳某种行为或加入某个社团时,不仅仅受周围朋友、同事和家人的影响,还受其他关系人群的影响。然而这些不同关系或渠道所产生的影响在很多情形中是不可叠加的。只有当某种关系(渠道)的影响达到某一条件时,个体才会采纳这种行为。鉴于此,Brummitt等[78]在多层耦合网络上应用Watts的阈值模型来研究。模型中节点只需在任一层处于活跃态的邻居比例超过某一阈值时,就变为活跃态。相比某单层网络具有与多层耦合网络相同拓扑结构时,发现无论是将两种具有不同交互方式的网络耦合还是将一个具有多种不可叠加关系的网络分成两个网络,都将促进全局级联的爆发。同样,Yagan等考虑到不同类型的连边往往对不同类型的社会传播(级联)起着不同大小的作用,例如在人群中推广一种新产品时,相对于家庭成员,一款游戏更容易被学校里面的同班同学推广;然而对于某种清洁产品,家庭成员却更易推广。基于这样的场景,他们研究不同类型边的相对重要性对耦合多层网络上线性阈值模型的影响[79]。他们假设网络中的边分为r类:1,…,r。对于某一内容(产品、观点、谣言等),考虑一个正的参数,c1,…,cr,其中ci表示第i种类型的边传播某一特定内容偏好性,ci越大表示这种内容更可能通过第i种边进行传递。对于一个阈值为τ的非活跃态节点它将变为活跃态,如果有
(2)
成立,其中节点有mi(ki)个第i种关系的活跃态邻居(邻居)节点。最后,他们发展了一套理论方法并得到级联爆发的条件,此外他们还发现在多层耦合网络上存在全局级联爆发的条件与最大连通子图的关系,而在单个网络上不存在这一关系。Cozzo等从理论分析的角度出发,基于马尔科夫链的方法,发展了一套耦合多层网络上社会传播的理论框架。同时他们分析得到行为采纳者和没有采纳行为的个体共存的条件,并发现耦合多层网络上的动力学主要取决于系统中单个网络邻接矩阵的最大特征值[80]。Min等考虑层间跨越的代价(节点在同层具有相同的传播率,节点在其中某层收到消息而在另一层去传播消息时,具有相对于同层更低的传播率)对信息在多层耦合网络上传播的影响,发现当两个网络层之间平均度差异较大时,爆发阈值随层间跨越的代价的增大而减小;当层间平均度差异较小时,爆发阈值随层间跨越的代价的增大呈现非单调性变化[63]等。

两个ER网络构成的双层耦合网络上,初始ρ0=10-3,在不同ε下,级联区域随平均度Z和响应阈值R的关系。其中灰色区域表示单个网络上的级联区域。实线和点线所包围左边区域表示级联能够发生,且实线和点线分别表示不连续相变和连续相变。
图2级联区域与响应阈值R和平均度Z的相图关系
Fig.2The (z,R)-phase diagram of global cascades
作为多层耦合网络上社会传播的进一步扩展,Lee等[81]考虑到大多数研究往往假设所有节点具有相同的动力学特征。然而,真实的复杂系统往往由不同的个体组成,它们对多层网络环境的应对方式往往不一样。比如,一个处于多层社交网络的个体,当他受到来自不同网络层的影响时,他是如何整合以及应对的呢?这往往取决于他的个体的特征以及社交网络公有的特性。鉴于此,Lee等在多层耦合网络中考虑比例节点响应阈值只需超过它某一网络阈值时就变为活跃态,其余1-ε比例节点需要两层同时超过其阈值才会变为活跃态,最后发现改变可以促进或者抑制级联的发生。当ε=1时,所有节点只需在其中一层超过阈值就变为活跃态,此时级联区域比单个网络要宽,即促进了级联爆发;随着ε的减少,越来越多的节点需要同时在两层超过阈值才能变为活跃态,级联区域越来越窄,抑制级联爆发,在抑制区域附近,级联随网络密度的增大出现不连续增加,如图2所示。
3多层耦合网络上的生物-社会耦合传播
多层耦合网络往往是由不同类型的网络层耦合而成,这些不同的网络层可供支持的动力学过程往往也不一样[82]。例如在线社交网络上的用户可以交互各种形式的信息,在物理接触网络上,个体之间可以传递带有疾病的生物元素等。Granell等[62]在多层耦合网络上研究疾病意识扩散和疾病传播构成的非对称耦合传播动力学。疾病意识在虚拟接触网络(这种类型的网络不需要物理接触可以相互通讯,例如Facebook, Twitters, etc)上扩散,用无意识态-意识态-无意识态模型来描述疾病意识的扩散过程。疾病本身在物理接触网络上传播,用经典的SIS模型来刻画。相对于没有意识到疾病到来的节点,意识到疾病到来的节点往往会采取相关措施,比如减少出行、戴面具等来保护自己,从而他们被疾病感染的概率更低。基于这种机制,他们发现多层网络的拓扑结构和两种动力学的相互关系共同确定流行病的阈值,此外,他们还基于微观马尔科夫链,发展了一套多层耦合网络上的非对称耦合传播动力学的解析方法,与模拟仿真吻合很好。作为对上述模型的进一步扩展,Granell等而后又考虑了大众媒体的影响[83],发现大众媒体会导致临界点的消失。Guo等考虑人类意识在扩散的过程中,个体往往会呈现从众行为,即个体在做决策时仿照周围邻居的决策。基于此,他们在多层耦合网络上提出局部意识控制疾病传播的模型。结果发现当局部意识的比值接近0.5时,疾病爆发阈值发生急剧的改变,从而导致对疾病爆发阈值和最终传播范围两个阶段的影响[84]。Massaro等考虑到个体知觉到的风险意识对有效传播率的影响。他们在多层耦合网络上研究疾病的风险意识对疾病传播的影响,发现当两个网络的结构越不相似时,越难控制疾病。最后他们还利用平均场的方法对模拟结果进行近似,并运用自组织的方法得到阈值[85]。
上述研究中,当个体意识到疾病到来的消息或察觉疾病到来的危机时,学者主要从降低易感性和风险意识的角度出发,在多层耦合网络上研究这些特性对疾病传播和控制的影响。Wang等直接从免疫的角度出发,考虑到疾病传播路径和消息传播途径的不同,建立由通讯网络(A)和接触网络(B)构成的多层耦合网络。关于疾病的消息在通讯网络(A)上传播,用类似于流行病的传播模型易感态-感染态-恢复态(SIR)进行描述;疾病本身则在接触网络(B)上传播,同样采用经典SIR流行病传播模型来建模,并引入了第4种状态免疫态(V)。个体在接触网络上被疾病感染时,他会立即获得关于疾病的消息,同时当个体在通讯网络上收到关于疾病的消息时,如果它在接触层仍处于S态,则以p的概率采取免疫行为,变成免疫态(V)。作者发现疾病消息的扩散抑制疾病传播,增大疾病的爆发阈值[61],如图3所示。当多层耦合网络的层间存在度关联时,他们还发现强的度关联对疾病消息传播的爆发阈值没有影响,但它却可以免疫一些大度节点从而抑制疾病的传播。同时,Wang等还发展了一套异质平均场的方法对该模型进行解析,能够较好地与模拟相对应。

a图形状为模拟值,而与之相同颜色的线为对应的理论值,插图表示接触层的最大连通子图存在的条件与和的关系;b图无标度网络和ER网络平均度均为8。
图3疾病爆发阈值与消息传播概率和免疫概率的关系
Fig.3Epidemic threshold versus the information-transmission rate and the raccination rate
最近许多研究表明,人类的行为采纳是一种复杂的非马尔科夫过程[9,11-12],个体采纳某种行为的概率与他收到行为消息的累积次数相关。Liu和Wang等最近考虑社会传播中的非马尔科夫特性——记忆性,对由疾病在接触网络上传播的同时,它所引起的疾病消息在另一通讯网络上的扩散反过来作用于疾病在接触网络上传播构成的非对称耦合传播动力学的影响。基于Wang等提出的模型[59],考虑当个体在接触网络上被疾病感染时,他会立即获得疾病消息;而与之区别的是当个体在通讯层收到疾病消息时,如果它在接触层仍处于S态,且该节点到该时刻为止累积收到M次消息,在加强效应强度为时,节点采取免疫行为的概率为:
ξM=ξ1+(1-ξ1)(1-e-α(M-1))
(3)
其中ξ1表示节点在通讯层只收到一次疾病消息且其对应在接触层的耦合节点仍处于S态时采取免疫行为的概率。考虑到被感染个体所需治疗的花费以及采取免疫行为的代价,Liu和Wang等研究这种加强效应的强度对传播动力学以及社会总花费的影响。最后发现,α抑制疾病传播,并增大疾病的爆发阈值。当考虑治疗和采取免疫行为的社会总花费时,发现存在一个最优α或者疾病消息传播率λAO使得总的社会花费最小。对于给定的参数(疾病传播率λB),在使得社会花费最优的过程中,最优α0随消息传播率λA的增大而减少;而对于最优λAO随α先上升再下降(当疾病传播率λB较大的情况下),如图4所示。此外,Liu和Wang等还发展了一套异质平均场的方法来验证模拟的正确性。
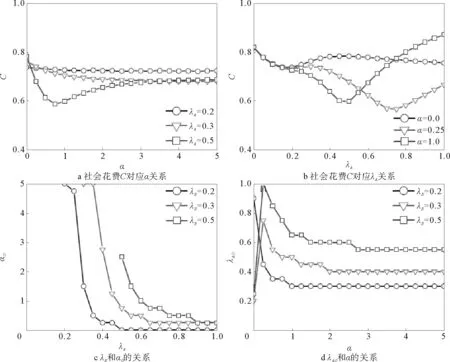
图4 通讯层(A)和接触层(B)分别为随机规则网络Regular Rule(RR)和随机网络(ER)构成的双层多层耦合网络
4多层耦合网络面临的挑战性问题
多层耦合网络上的传播动力学研究还是一个刚兴起的领域,有很多课题亟待研究解决。比如,单个网络上一些很容易解释的动力学现象在多层耦合网络上却很难去解释。多层耦合网络上的实证、理论、算法等方法都需要进一步开拓创新,而不是简单地从已有关于单个网络上对应的分析方法中拓展过来。为此,本节提出多层耦合网络面临的一些挑战性问题。
4.1基于数据的多层耦合网络的实证分析
一直以来,实证分析是我们认识世界的一种重要方法和手段,并通过在实证分析中找到规律引领人类前进,推动社会发展。目前,在多层耦合网络上进行实证分析,还存在两个难点:大数据收集和分析方法。相对于单个网络,关于多层耦合网络数据收集更难,涉及方面更广。例如,对于在线社交网络这种类型的数据,早期对于单一社交网络上数据的收集一般只涉及到一家社交网络公司,无论是通过网络爬虫或者公司提供都比较容易得到。然而,对于多层耦合网络,至少涉及到两个或以上是社交网络公司,考虑到用户个人资料以及相关的利益等问题往往很难达成共识。同时,由于用户在不同社交网络上的注册信息不一样,通过爬虫的方法得到的数据不能确定同一个用户在不同社交网络上的账号等等。多层耦合网络具有比单个网络更复杂的结构和非结构数据,同时存在多种动力学之间相互作用过程,无论对多层耦合网络结构本身还是其上真实传播过程的分析,都极具挑战性。
4.2多层耦合网络在中尺度结构上对传播的影响
社区结构[84]是网络在中尺度上一个特别重要的属性。并且对传播有着特别的作用,例如,在具有较强社区结构的单个网络上,社会加强效应更明显[87],从而促进消息、行为等在局部的传播;而在社区结构不明显的网络上,较多桥连边的存在使得传播更易在全局爆发。当考虑两个或多个网络耦合,并且整个多层耦合网络上分别有一种或多种动力学时,各个网络层在中尺度上的社区结构的相似性(比如节点的重叠度、边的重叠度),以及各层社区之间的关联性(层间度关联、节点在各层群集系数的关联性等),究竟对多层耦合网络上的动力学过程有何影响呢?特别地,当两种具有非对称作用的动力学过程同时在多层耦合网络上传播时,比如疾病消息—疾病,如果各层网络的社区结构之间没有公共的交集(节点、边),这两种动力学相当于各自在孤立的网络上传播并没有形成具有非对称作用的耦合传播。想简单地通过多种动力学之间的非对称耦合作用来控制传播,这一问题值得深思和进一步研究。
4.3网络动力学和传播动力学演化的时间尺度对多层耦合网络上传播的影响
对于多层耦合网络,各层网络往往蕴含着不同的社会背景,比如在线社交网络和物理接触网络构成的多层耦合网络,前者是基于因特网而形成的交互方式,而后者是人们线下面对面的交互方式。这两种具有不同社会背景的网络所对应网络动力学演化的时间尺度往往是不相同的(前者演化得更快些),当它们支持的动力学过程(比如均为信息传播)在该多层耦合网络上传播时,这种时间尺度的差异对传播有何影响呢? 此外,一般情况下,不同的网络层可供支持的动力学过程不一样,对应传播动力学演化的时间尺度也不一样,比如仍在上述多层耦合网络中,在线社交网络上传播信息是以秒、分钟为单位,物理接触网络上疾病感染往往是以天、周等为单位,这种传播动力学演化本身的时间尺度差异多对于传播又有何影响呢?此外,当网络动力学和传播动力学演化的时间尺度差异同时存在时,这对多层耦合网络上传播又有何影响呢?这一系列问题是非常值得深思探讨的,无论是对于其中单一动力学的演化还是两种动力学的共同演化,弄清它们相互交织影响的规律对解释、预测、控制真实的传播过程非常必要,非常具有挑战性。
4.4多层耦合网络上的节点影响力排序
如何用定量分析方法识别网络中哪些节点最具有影响力, 或者评价某个节点相对其他节点的重要程度是复杂网络亟待解决的重要课题之一。在单个网络上,已有很多评价指标,如考虑节点的局部属性的度,或者邻居信息[88]、基于网络全局指标的特征向量[89]、基于网络位置属性指标k-core[90]、基于传播动力学的节点重要性[91],等等。在多层耦合网络上,不仅需要考虑节点同时在两层网络结构特性[92],还需考虑两层网络上的不同动力学过程。如在信息-疾病构成的非对称耦合传播动力学上[61],一个节点在信息层能促进信息传播的同时还会抑制疾病在接触层的传播。这时,基于某个网络上节点的影响力排序不再适于整个多层耦合网络节点的排序,需要同时考虑两种动力学之间的作用才能更好、更准确地对多层耦合网络上的节点排序。
4.5多层耦合网络的免疫策略
免疫策略的研究是为了控制传播,减少传播对人类造成的危害。目前在单个网络上的免疫策略有:基于网络全局结构的目标免疫[38-41]、基于局部结构信息的熟人免疫[42]、随机免疫[1]等。这些免疫策略很大程度上是基于单一网络上单一动力学而设计的。然而在这一具有更为复杂的网络结构特性,可同时支持多种动力学过程的多层耦合网络上,所需考虑的不仅仅是某一层网络的结构特性和某一层的动力学过程。例如,同一种疾病在由两个网络层构成的耦合网络上传播,取度这一结构特性进行免疫时,某一类节点在其中一层是大度节点,而对应在另一层是小度节点,而另一类节点在两层具有相同大小的度,且这两类节点在两层的度之和相同,免疫哪类的节点能更有效地控制疾病传播呢?此外,对由不同动力学过程在多层耦合网络上传播时,例如,信息-疾病二者构成具有非对称作用的生物-社会耦合传播,免疫其中一个节点时(对应在两层均免疫,不传播消息和疾病),抑制疾病层传播的同时,还抑制了消息层的扩散,从而减少了对疾病层的抑制作用,在这种情形下,如何设计免疫策略能够最有效地控制疾病传播呢?当多层耦合网络的结构特性和各层的动力学作用同时需要考虑时,又该如何选择免疫策略呢?等等,这一系列问题还有待于进一步研究。
4.6多层耦合网络上传播路径预测及还原
一直以来,花费最少的时间识别传播源是传播动力学中一个非常具有挑战性和实际意义的问题。例如,埃博拉最近在西非地再次爆发,如果能够及时准确地找到传播源,医疗卫生组织就有足够多的时间对该病毒的生存环境、病症、传播途径分析,这对有效控制病毒传播避免过多的人员伤亡是非常有意义的。目前,对于单个网络上传播源的识别方法主要有信息传递[93]和压缩感知的方法[36]。然而对于具有更复杂结构特性的多层耦合网络,可供传播的路径除了各层网络本身外,还可以层间跨越的方式在多层耦合网络上传播,这对于传播源的识别无疑是更大的挑战。已有的这些方法是否仍适用和有效?目前尚缺乏研究多层耦合网络上传播源识别以及相应的理论框架,这是一个值得研究的挑战性问题!
5展望
在人类科学研究的历史长河中,人们一直秉持着先简单后复杂的分析方法去探讨、研究自然现象和人类社会中的各种各样问题。同样,网络科学研究也是从单一网络开始,正在向现实世界具有多层次“网络的网络”或超网络的方向发展之中。自然,作为网络科学一个重要课题的网络传播动力学也不例外。早期,为了分析、建模以及理论解析简便性,主要是在单个网络上研究传播动力学过程。然而,随着研究的不断深入,单个网络上的模拟仿真不再适合真实社会的场景。因此,必然正在从单一网络上的传播动力学的研究拓展到多层耦合网络上,更广泛意义地说,在研究“网络的网络”或超网络上的传播动力学,并尽量使得研究结果与现实网络中的现象更接近、更符合实际规律,以便人类能够更准确地预测和控制疾病、谣言、社会行为等传播,最终达到完全管控网络传播变害为利的目的。
本文对迄今多层耦合网络上传播动力学的研究成果作了比较系统的综述,我们看到在国内外学者的共同努力下,迄今研究取得了可喜的进展。诸如,发现相对于单一网络上生物或者社会传播,在多层耦合网络上这些传播过程更易爆发;同时还存在各种有趣的相变现象;而对于多层耦合网络上的生物—社会耦合传播,发现两个网络的结构越不相似,越难控制疾病,等等。这些初步成果为进一步深入探索网络传播的“庐山真面目”打下了坚实的理论基础。
同时,我们更清醒地认识到:在具有多层的“网络的网络”或超网络上的传播动力学研究,正面临着许多新的挑战性课题。如上所述,基于人类行为动力学和大数据的多层耦合网络上传播怎么深入进行实证分析,需要探索中观尺度网络结构及其网络动力学的规律,各层各自时间尺度的差异对传播动力学怎么影响,节点影响力排序、免疫策略和追溯传播路径以及涉及超网络金字塔的传播等都是值得深入探索的重要课题。
感谢方锦清教授在本文撰写过程中提出的宝贵意见。
参考文献:
[1]Anderson R M, May R M. Infectious Diseases in Humans [M]. Oxford: Oxford University Press, 1992.
[2]Pastor-Satorras R, Vespignani A. Epidemic spreading in scale-free networks [J]. Phys Rev Lett, 2001, 86(14): 3200-3203.
[3]Shu P, Tang M, Gong K, et al. Effects of weak ties on epidemic predictability on community networks [J]. Chaos, 2012, 22(4), 043124.
[4]Tang M, Liu Z, Li B. Epidemic spreading by objective traveling[J]. Europhys Lett, 2009, 87(1): 18005.
[5]Wang W, Tang M, Zhang H F, et al. Epidemic spreading on complex networks with general degree and weight distributions [J]. Phys Rev E, 2014, 90: 042803.
[6]Shu P, Wang W, Tang M, et al. Numerical identification of epidemic threshold for susceptible-infected-recovered model on finite-size [J]. Chaos, 2015, 25:063104.
[7]Young H P. The dynamics of social innovation [J]. Proc Natl Acad Sci USA, 2011, 108: 21285-21291.
[8]Montgomery R L. The diffusion of religions [D]. Lanham: University Press of America, 1996.
[9]Centola D. An experimental study of homophily in the adoption of health behavior [J]. Science, 2011, 334:1269-1271.
[10] Wang W, Tang M, Zhang H F, et al. Dynamics of social contagions with memory of nonredundant information [J]. Phys Rev E, 2015, 92: 012820.
[11] Granovetter M. Threshold models of collective behavior [J]. Am J Sociol, 1973, 78: 1360.
[12] Watts D J. A simple model of global cascades on random networks [J]. Proc Natl Acad Sci USA, 2002, 99: 5766-5771.
[13] Daley D J, Kendall D G. Epidemics and rumours [J]. 1964, 204:1118-1118.
[14] Zheng M, L L, Zhao M. Spreading in online social networks: the role of social reinforcement [J]. Phys Rev E, 2013, 88(1):012818.
[15] Meyers L A, Pourbohloul B, Newman M E J, et al. Network theory and SARS: predicting outbreak diversity [J]. J Theor Biol, 2005, 232: 71-81.
[16] Hufnagel L, Brockmann D, Geisel T. Forecast and control of epidemics in a globalized world [J]. Proc Natl Acad Sci USA, 2004, 101: 15124.
[17] Garten R J, Davis C T, Russell C A, et al. Antigenic and genetic characteristics of swine-origin 2009 A (H1N1) influenza viruses circu lating in humans [J]. Science, 2009, 325: 197-201.
[18] Leroy E M, Rouquet P, Formenty P, et al. Multiple ebola virus transmission events and rapid decline of central african wildlife [J]. Science, 2004, 303: 387-390.
[19] Pastor-Satorras R, Castellano C, Van Mieghem P, et al. Epidemic processes in complex networks [DB/OL].[2015-08-22]. http://arxiv.org/abg/1408.2701.
[20] Pastor-Satorras R, Vespignani A. Epidemic dynamics in finite size scale-free networks [J]. Phys Rev E, 2002, 65:035108(R).
[21] Wang R S, Albert R. Effects of community structure on the dynamics of random threshold networks [J]. Phys Rev E, 2013, 87: 012810.
[22] Newman M E J. Random graphs with clustering [J]. Phys Rev E, 2009, 103: 058701.
[23] Barthelemy M, Barrat A, Pastor-Satorras R, et al. Velocity and hierarchical spread of epidemic outbreaks in scale-free networks [J]. Phys Rev E, 2004, 92: 178701
[24] Ruan Z, Tang M, Liu Z. How the contagion at links influences epidemic spreading [J]. The European Physical Journal B, 2013, 86(4): 1-6.
[25] Zhu Y X, Zhang X G, Sun G Q, et al. Influence of reciprocal links in social networks [J]. PLoS ONE, 2014, 9(7): e103007.
[26] Cui A X, Wang W, Tang M, et al. Efficient allocation of heterogeneous response times in information spreading process [J]. Chaos, 2014, 24: 033113.
[27] Barthelmy M, Barrat A, Pastor-Satorras R, et al. Velocity and hierarchical spread of epidemic outbreaks in scale-free networks[J]. Phys Rev E, 2004, 92: 178701.
[28] Boguna M, Pastor-Satorras R, Vespignani A. Absence of epidemic threshold in scale-free networks with degree correlations [J]. Phys Rev Lett, 2003, 90(2): 028701.
[29] Boguna M, Castellano C, Pastor-Satorras R. Nature of the epidemic threshold for the susceptible-infected-susceptible dynamics in networks [J]. Phys Rev Lett, 2013, 111(6): 068701.
[30] Castellano C, Pastor-Satorras R. Thresholds for epidemic spreading in networks [J]. Phys Rev Lett, 2010, 105: 218701.
[31] Kitsak M, Gallos L K, Havlin S, et al. Identification of influential spreaders in complex networks [J]. Nat Phys, 2010, 6:888-893.
[32] Liu Y, Tang M, Zhou T, et al. Core-like groups resulting in invalidation of k-shell decomposition analysis [J]. Sci Rep, 2014, 5(9602):.
[33] Zhong L F, Liu J G, Shang M S. Iterative resource allocation based on propagation feature of node for identifying the influential nodes [DB/OL]. [2015-06-08]. http://dx.doi.org/10.1016/j.physleta.2015.05.021.
[34] Zhao X Y, Huang B, Tang M, et al. Identifying effective multiple spreaders by coloring complex networks [J]. Europhys Lett, 2014, 108(6): 68005.
[35] Liu Y, Tang M, Zhou T, et al. Improving the accuracy of the k-shell method by removing redundant links-from a perspective of spreading dynamics [DB/OL].[2015-08-06]. http://arxiv.org/pdf/ 1505.07354.pdf.
[36] Shen Z, Wang W X, Fan Y, et al. Reconstructing propagation networks with natural diversity and identifying hidden sources [J]. Nat Commun, 2014, 5:4323.
[37] Brockmann D, Helbing D. The hidden geometry of complex network-driven contagion phenomena [J]. Science, 2013, 342: 1337-1442.
[38] 王伟,杨慧,龚凯,等. 复杂网络上的局域免疫研究 [J]. 电子科技大学学报,2013,42(6),817-830.
Wang Wei, Yang Hui, Gong Kai, et al. Local immunization algorithm on complex networks[J], Journal of University of Elec tronic Science and Technology of China, 2013, 42(6): 817-830.
[39] Pastor-Satorras R, Vespignani A. Immunization of complex networks [J]. Phys Rev E, 2002, 65: 036104.
[40] Zhang H F, Shu P P, Tang M, et al. Preferential imitation of vaccinating behavior can invalidate the targeted subsidy on complex net work [J]. arXiv, 2015, arXiv:1503.08048.
[41] Cohen R, Havlin S, Ben-Avraham D. Efficient immunization strategies for computer networks and populations [J]. Phys Rev Lett, 2003, 91: 247901.
[42] Ruan Z, Tang M, Liu Z. Epidemic spreading with information-driven vaccination [J]. Phys Rev E, 2012, 86, 036117.
[43] Yang H, Tang M, Zhang H F. Efficient community-based control strategies in adaptive networks [J]. New J Phys, 2012, 14: 123017.
[44] Singh P, Sreenivasan S, Szymanski B K, et al. Threshold-limited spreading in social networks with multiple initiators [J]. Sci Rep, 2013, 3: 2330.
[45] Nematzadeh A, Ferrara E, Flammini A, et al. Optimal network modularity for information diffusion [J]. Phys Rev Lett, 2014, 113: 088701.
[46] Gleeson J P, Cahalane D J. Seed size strongly affects cascades on random networks [J]. Phys Rev E, 2007, 75: 056103.
[47] Gleeson J P. Cascades on correlated and modular random networks [J]. Phys Rev E, 2008; 77: 046117.
[48] Kempe D, Kleinberg J, Tardos E. Maximizing the spread of influence through a social network [C]//ACM SIGKDD, 2003, 137-146.
[49] Chen W, Yuan Y, Zhang L. Scalable influence maximization in social networks under the linear threshold model [C]//IEEE ICDM, 2010, 88-97.
[50] Karimi F, Holme P. Threshold model of cascades in empirical temporal networks [J]. Physica A, 2013, 392:3476-3483.
[51] Funk S, Gilad E, Watkins C, et al. The spread of awareness and its impact on epidemic outbreaks [J]. Proc Natl Acad Sci USA, 2009, 106: 6872-6877.
[52] Funk S, Gilad E, Jansen V A A. Endemic disease, awareness, and local behavioural response [J]. Journal of theoretical biology, 2010, 264: 501-509.
[53] Zhang H F, Wu Z X, Tang M, et al. Effects of behavioral response and vaccination policy on epidemic spreading-an approach based on evolutionary-game dynamics [J]. Sci Rep, 2014, 4(5666).
[54] Zhang H F, Xie J R, Tang M, et al. Suppression of epidemic spreading in complex networks by local information based behavioral responses [J]. Chaos: an Interdisciplinary Journal of Nonlinear Science, 2014, 24(4): 043106.
[55] Boccaleti S, Bianconi G, Criado R, et al. Structure and dynamics of multilayer networks [J]. Phys Rep, 2014, 544:1-122.
[56] Kivel M, Arenas A, Barthelemy M, et al. Multilayer networks [J]. J Complex Netw, 2014, 2:203-271.
[57] Buldyrev S V, Parshani R, Paul G, et al. Catastrophic cascade of failures in interdependent networks [J]. Nature, 2010, 464:2015-2028.
[58] Parshani R, Buldyrev S V, Havlin S. Interdependent networks: reducing the coupling strength leads to a change from a first to second order percolation transition [J]. Phys Rev Lett, 2010, 105: 048701.
[59] Xu X L, Qu Y Q, Guan S, et al. Interconnecting bilayer networks [J]. Europhy Lett, 2011, 93:68002.
[60] Wang W, Tang M, Yang H, et al. Asymmetrically interacting spreading dynamics on complex layered networks [J]. Sci Rep, 2014, 4:5097.
[61] Granell C, Gmez S, Arenas A. Dynamical interplay between awareness and epidemic spreading in multiplex networks [J].Phys Rev lett,2013,111: 128701.
[62] Min B, Goh K I. Layer-crossing overhead and information spreading in multiplex social networks[DB/OL].[2015-08-06].http://arxiv.org/pdf/1307.2967.pdf.
[63] Gao J X, Buldyrev S V, Havlin S, et al. Robustness of a network of networks [J]. Phys Rev Lett, 2011,107:195701.
[64] Vespignani A. The fragility of interdependency [J]. Nature, 2010,464:984-985.
[65] Wang Z, Wang L, Perc M. Degree mixing in multilayer networks impedes the evolution of cooperation [J]. Phys Rev E, 2014, 89:052813.
[66] Wang Z, Szolnoki A, Perc M. Optimal interdependence between networks for the evolution of cooperation [J]. Sci Rep, 2013, 3(2470).
[67] Aguirre J, Sevilla-Escoboza R, Gutirrez R, et al. Synchronization of interconnected networks: the role of connector nodes [J]. Phys Rev Lett, 2014, 112(24), 248701.
[68] Barreto E, Hunt B, Ott E, et al. Synchronization in networks of networks: the onset of coherent collective behavior in systems of interacting populations of heterogeneous oscillators [J]. Phys Rev E, 2008, 77(3), 036107.
[69] Zhang X Y, Boccaletti S, Guan S G, et al. Explosive synchronization in adaptive and multilayer networks [J]. Phys Rev Lett, 2015, 114, 038705.
[70] Saumell-Mendiola A, Serrano M, Bogun M. Epidemic spreading on interconnected networks [J]. Phys Rev E, 2012, 86: 026106.
[71] Dickison M, Havlin S, Stanley H E. Epidemics on interconnected networks [J]. Phys Rev E, 2012, 85: 066109.
[72] Wang H, Li Q, D’Agostino G, et al. Effect of the interconnected network structure on the epidemic threshold [J]. Phys Rev E, 2013, 88(2): 022801.
[73] Buono C, Alvarez-Zuzek L G, Macri P A, et al. Epidemics in partially overlapped multiplex networks [J]. PloS ONE, 2014, 9(3): e92200.
[74] Zhao D, Wang L, Li S, et al. Immunization of epidemics in multiplex networks [J]. PLoS ONE, 2014, 9(11): e112018.
[75] Elvis H W, Wang X W, Xu C, et al. Suppressed epidemics in multi-relational networks [DB/OL].[2015-08-06].http://journals.aps.org/pre/abstract/10.1103/Phys Rev E.92.022812.
[76] 李睿琪, 唐明, 许伯铭. 多关系网络上的流行病传播动力学研究 [J]. 物理学报, 2013, 62(16): 168903-168903.
Li Ruiqi, Tang Ming, XU Boming. Epidemic spreading on multi-relational networks[J]. Acta Phys Sin, 2013, 62(16): 168903.
[77] Brummitt C D, Lee K M, Goh K I. Multiplexity-facilitated cascades in networks [J]. Phys Rev E, 2012, 85:045102(R).
[78] Yagan O, Gligor V. Analysis of complex contagions in random multiplex networks [J]. Phys Rev E, 2012, 86(3):036103.
[79] Cozzo E, Banos R A, Meloni S, et al. Contact-based social contagion in multiplex networks [J]. Phys Rev E, 2013, 88(5): 050801.
[80] Lee K M, Brummitt C D, Goh K L. Threshold cascades with response heterogeneity in multiplex networks [J].Phys Rev E, 2014, 90:062816.
[81] Bauch C T, Galvani A P. Social factors in epidemiology [J]. Science, 2013, 342:47-49.
[82] Granell C, Gmez S, Arenas A. Competing spreading processes on multiplex networks: awareness and epidemics [J]. Phys Rev E, 2014, 90: 012808.
[83] Guo Q T, Jiang X, Lei Y J, et al. Two-stage effects of awareness cascade on epidemic spreading in multiplex networks [J]. Phys Rev E, 2015, 91: 012822.
[84] Massaro E, Bagnoli F. Epidemic spreading and risk perception in multiplex networks: a self-organized percolation method [J]. Phys Rev E, 2014, 90: 052817.
[85] Fortunato S. Community detection in graphs [J]. Phys Rep, 2010, 486: 75-174.
[86] Rogers E. The Diffusion of Innovations [M]. fifth ed. New York: Free Press, 1995.
[87] Newman M E J. Networks: an Introduction [M]. Oxford: Oxford University Press, 2010.
[88] Newman M E J. The structure and function of complex networks [J]. SIAM Rev, 2003, 45:167-256.
[89] Kitsak M, Gallos L K, Havlin S, et al. Identification of influential spreaders in complex networks [J]. Nat Phys, 2010, 6:888-893.
[90] Aral S, Walker D. Identifying influential and susceptible members of social networks [J]. Science, 2012, 337:337-341.
[91] Domenico M D, Solé-Ribalta A, Omodei E, et al. Ranking in interconnected multilayer networks reveals versatile nodes[J]. Nat Com Mun, 2015, 6:6868.
[92] Lokhov A Y, Mézard M, Ohta H, et al. Inferring the origin of an epidemic with a dynamic message-passing algorithm [J]. Phys Rev E, 2014, 90: 012801.
[93] 方锦清,唐明,面临NON前沿课题的挑战与网络传播的若干研究进展,2015第11届中国网络科学论坛大会报告 [R].上海:上海大学,2015.
Fang Jinqing, Tang Ming. Facing the challenge of NON frontier subject and the progress of spreading dynamics on network(in Chinese) . The 11 th network science conference of China in 2015[R]. Shanghai:University of Shanghai,2015.
[94] Fang J Q,Tang M. Network Science Faces the Challenge and Opportunity: Exploring "network of networks" and its unified theoretical framework [J], to be published, 2015.
[95] 方锦清,探索超网络金字塔,超图与超网络专题研讨会 [R].西宁,2015.
Fang Jinqing. The workshop of exploring the super network pyramid, hypergraph and super network(in Chinese) [R]. Xining,2015.
(责任编辑李进)
The Review of Spreading Dynamics on Multilayer Coupled Networks
LIU Quanhui, WANG Wei, TANG Ming
( Web Science Center,University of Electronic Science and Technology of China,Chengdu 611731,China)
Abstract:For a long time, spreading dynamics is a very important subject in network science. Recent studies on the spreading dynamics on the multilayer coupled networks attract attention both at home and abroad. This review article introduces the progress of spreading dynamics on the multilayer coupled networks and some open questions, mainly focusing on the following four aspects: (1) biological spreading on the multilayer coupled networks; (2)social contagion on the multilayer coupled networks; (3) biological-social coupling transmission on the multilayer coupled networks; and (4) some problems on multilayer coupled networks. These episodes of research from a new angle of multilayer coupled network deepened our understanding of the real propagations. The problems discussed here will help to clear the direction of next stage.
Key words:network science; multilayer coupled networks; spreading dynamics
文章编号:16723813(2016)01004810;
DOI:10.13306/j.1672-3813.2016.01.003
收稿日期:2015-08-24
基金项目:国家自然科学基金(11575041)
作者简介:刘权辉(1990-),男,湖南邵阳人,博士研究生,主要研究方向为复杂网络传播动力学。
通信作者:唐明(1981-),四川资阳人,博士,副教授,主要研究方向为网络科学理论,网络传播动力学。
中图分类号:N94;N93
文献标识码:A

