三维空间中Euler方程的中心差分方法

唐秀丽，王修庆

(云南民族大学 数学与计算机科学学院，昆明 云南　650500)

三维空间中Euler方程的中心差分方法

唐秀丽，王修庆

(云南民族大学 数学与计算机科学学院，昆明 云南650500)

摘要：Euler方程在流体动力学中扮演着极为重要的角色，目前，仅仅在理论上取得了很少的突破。对于Euler方程的研究，难度特别大。因而主要从数值解方面入手，对三维Euler方程的初边值问题建立了中心差分格式，并分析了截断误差。 最后，通过Matlab 数值模拟了差分结果，并与精确解进行了误差比较，验证了理论结果。

关键词：Euler方程；中心差分格式；精确解；截断误差

0引言

Euler方程是无粘性流体力学中最重要的方程之一。1755年，瑞士数学家和物理学家Euler在《流体运动的一般原理》一书中首次提出无粘性流体运动力学中最重要的基本方程-- Euler方程。目前，Euler方程在工业、农业、交通运输、天文学、地学，生物学和医学等领域都已得到了广泛的应用。为此，众多学者针对Euler方程开展了相关研究，由于Euler方程的理论研究[1-4]难度较大，进展缓慢，让人们不知从何入手，而数值解可以给Euler 方程的研究提供一些信息[5-9]。从三维Euler方程着手，建立其中心差分格式,给出差分方法格式的解与精确解的误差。

本文研究如下形式的三维Euler方程：

(1)

其中u=(u1,u2,u3)，ui=ui(x,y,z,t)(i=1,2,3)，p=p(x,y,z,t)。

1三维Euler方程中心差分格式与截断误差

1.1中心差分格式

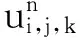
建立方程(1) 的中心差分格式:

为了计算简便，可将上式化解为如下形式：

1.2截断误差

对于方程(1)的解u(x,y,z,t),p(x,y,z,t)，关于t的向前差分的Taylor级数展开有

对变量x的中心差分格式进行Taylor级数展开有

故截断误差为

所以有

T1(x,y,z,t)=ο(τ+h2), T2(x,y,z,t)=ο(τ+h2),

T3(x,y,z,t)=ο(τ+h2), T4(x,y,z,t)=ο(h2)。

2三维Euler方程中心差分格式的解与精确解的误差

2.1作图

参考文献[10,11]取Euler方程的精确解为：

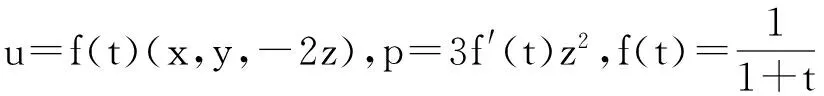
对应的初边值为：

初始值

左边界值

右边界值

对MATLAB计算中相关数值，我们分别取如下两组数据：

x0=-1,y0=-1,z0=-1,t0=0

h0=1.5,τ0=2,h=0.1,τ=0.1

及x0=0,y0=0,z0=0,t0=0

h0=2,τ0=2,h=0.1,τ=0.1。

差分解、精确解和误差的图像见图：

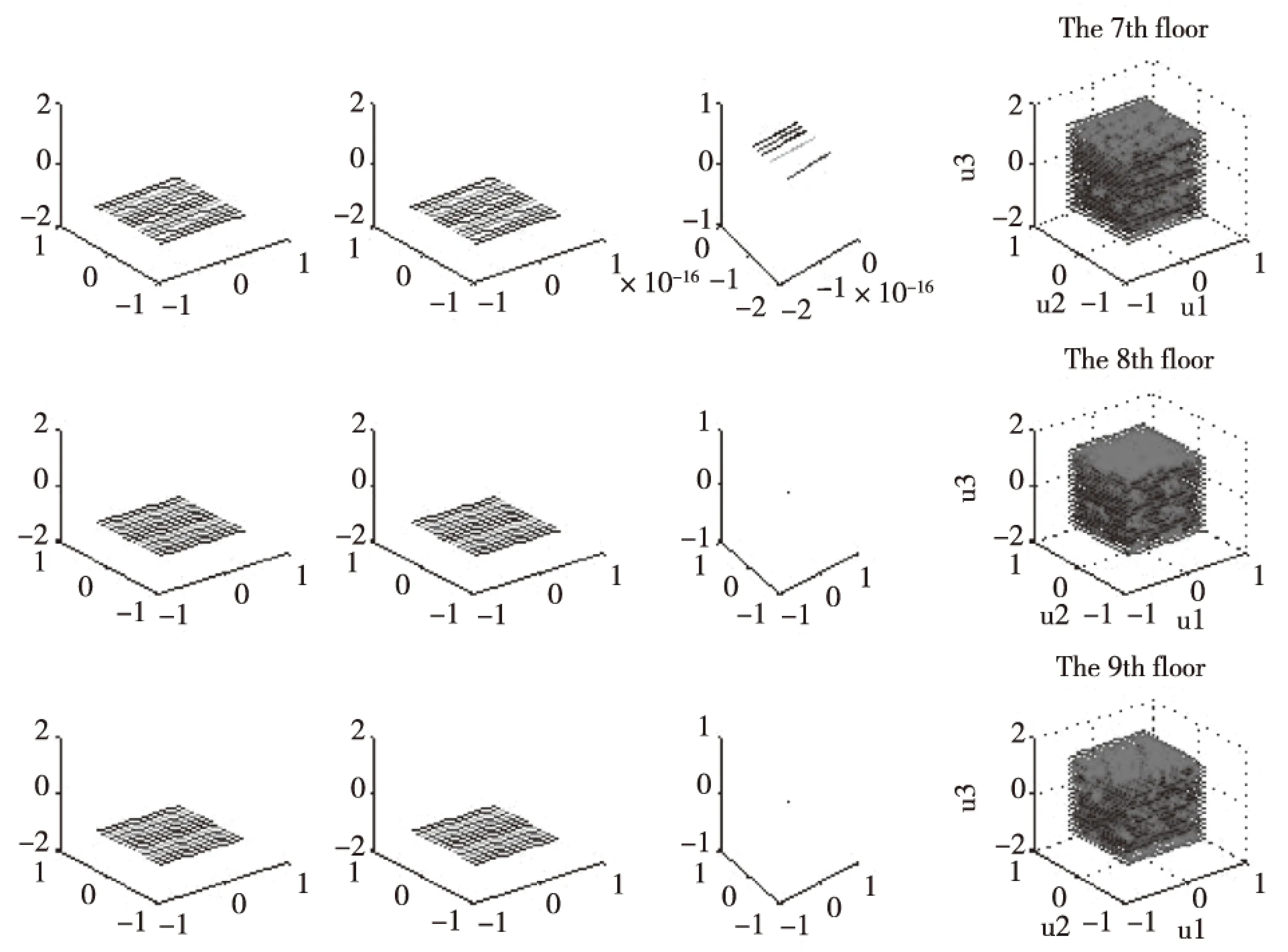
图1　数据组1Fig.1　Data set 1

图2　数据组2Fig.2　Data set 2

图中每行从左至右分别为真值图、数值解的图、两者的误差图以及两者的比较图。

2.2误差分析

由图像可知：

每一列分别表示当时间层取1,2,…,14,15时相应的真值图、差分解的图，两者的误差图和两者的比较图。对第一组数据， 随着t 的增大，吻合程度越来越高，当 t=8-9 时，误差达到最小，为零。对第二组数据， 随着t 的增大，吻合程度越来越高，当t=10 时，误差达到最小，为零。

3收敛性分析

对上节所给出的方程(1)的初边值问题，做出中心差分格式数值解相邻两层差值的标准差如下：

fork=1

u11(i,j,l)=(u11(i+1,j+1,1,l+1)-u11(i,j,1,l))2

u21(i,j,l)=(u21(i+1,j+1,1,l+1)-u21(i,j,1,l))2

u31(i,j,l)=(u11(i+1,j+1,1,l+1)-u11(i,j,1,l))2

fork=2:M-1

u11(i,j,l)=u11(i,j,l)+(u11(i+1,j+1,k+1,l+1)-u11(i,j,k,l))2

u21(i,j,l)=u21(i,j,l)+(u21(i+1,j+1,k+1,l+1)-u21(i,j,k,l))2

u31(i,j,l)=u31(i,j,l)+(u31(i+1,j+1,k+1,l+1)-u31(i,j,k,l))2

再令

对上节所给出的方程(1)的初边值问题的第一组数据，分别取不同的时间步长和空间步长， 做出中心差分格式数值解相邻两层差值的标准差图像，如下：

图3，图4表示在时间与空间步长越来越细的时候，中心差分数值解每相邻两层的差值标准差图像。分析图像可知，随着时间的推移，时间层数的增加，数值解间的距离趋于零。所以Euler方程组(1)的中心差分格式是收敛的。

图3　dt=0.05，dx=dy=dz=0.1Fig.3　dt=0.05,dx=dy=dz=0.1

[1] QUARTAPELLE L.Incompressible Euler equations[J].Birkhäuser Basel,1993,113:209-242.

[2] POPINET S.Gerris:a tree-based adaptive solver for the incompressible Euler equations in complex geometries[J].Journal of Computational Physics,2003,190(2):572-600.

[3] COUTAND D,SHKOLLER S.Well-posedness of the free-surface incompressible Euler equations with or without surface tension[J].Journal of the American Mathematical Society,2005,20(3):829-930.

[4] LIU T P,YANG T.Compressible Euler equations with Vacuum[J].Commun Phys,1985,101:475-485.

[5] 陆金甫,关治.偏微分方程数值解法(第2版)[M].北京:清华大学出版社,2003.

[6] 张德喜,赵磊生.MATLAB 语言程序设计教程(第二版)[M].北京:中国铁道出版社,2010.

[7] 张天德,张希华,王玮.偏微分方程差分格式的构造[J].山东工业大学学报,1997,27(3):227-231.

[8] 罗志强,陈志敏.Euler方程有限差分方法数值模拟[J].南开大学学报(自然科学版),2012(1):1-7.

[9] CHRISTIANSEN T B,BINGHAM H B,ENGSIG-KARUP A P.High-Order Finite Difference Solution of Euler Equations for Nonlinear Water Waves[J].Asme International Conference on Ocean,2012:519-528.

[10]GUO B L,YANG G S,PU X K.Blow-up and global smooth solutions for incompressible three-dimensional Navier-Stokes equations[J].Chin Phys Lett,2008,25(6):2115-2117.

[11]SONG W J,LI H,YANG G H,et al. Nonhomogeneous boundary value problem for (I, J) similar solutions of incompressible two-dimensional Euler equations[J].Journal of Inequalities and Applications,2014(1):1-15.

Central difference scheme of Euler equation in three dimensional spaces

TANG Xiuli，WANG Xiuqing

(Department of Mathematics, Yunnan Nationalities University，Kunming，Yunnan 650500,China)

Abstract:Euler equation plays an essential part in the learning of analytical dynamics. So far, there is not much theoretical breakthrough in this area. This paper will mainly propose a central difference method for the initial boundary value problem of Euler Equation and analysis the truncation errors of it. Finally, the numerical experiments through Matlab are provided to check the theoretical results.

Key words:Euler equation；central difference scheme； exact solution；truncation error

文章编号：1004—5570(2016)02-0071-05

收稿日期：2015-12-01

基金项目：国家自然科学基金资助项目(No.11561076)；云南民族大学研究生创新基金项目(No.2015YJCXY284)

作者简介：唐秀丽(1991-)，女，硕士，研究方向：偏微分方程，E-mail:tangxiuli1991@126.com.

中图分类号：O241.3

文献标识码：A