NA样本下Lindley分布参数的经验Bayes检验
范梓淼,周菊玲
(新疆师范大学 数学科学学院,新疆 乌鲁木齐 830017)
NA样本下Lindley分布参数的经验Bayes检验
范梓淼,周菊玲*
(新疆师范大学 数学科学学院,新疆 乌鲁木齐830017)
摘要:基于NA随机样本序列,讨论了Lindley分布的参数θ的经验Bayes检验函数问题H0:θ≤θ0↔H1:θ>θ0。结论:构造了参数的经验Bayes检验函数,并获得其渐近最优性;在适当条件下证明了经验Bayes检验函数的收敛速度)。
关键词:NA样本;Lindley分布:经验Bayes检验
0引言
Lindley分布由Lindley于1958年提出,但直到最近几年才被学者关注。Zamani等学者将该分布应用于交通事故分析。Ghitany在文[1]中利用Lindley分布模型拟合寿命数据,发现比用指数分布模型更好,并且指出Lindley分布具有的很多数学性质比指数分布的还要灵活。在应力-强度模型的可靠性研究中该分布也起着重要的作用。因此对Lindley分布的统计性质研究是非常必要的。文[2]中在独立同分布样本下讨论了Lindley分布参数的单侧检验问题,文[3]讨论了Lindley分布参数的区间估计和假设检验。该分布在NA样本下的讨论非常罕见,鉴于此,本文在NA样本情形下,讨论该分布参数的经验Bayes检验。

定义2[5]称随机变量X服从Lindley分布,如果其概率函数为
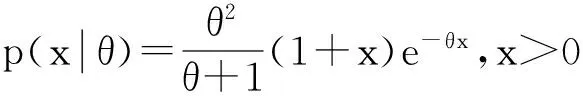
1经验Bayes检验
首先建立Lindley分布参数θ的如下一对假设检验:
H0:θ≤θ0↔H1:θ>θ0
设行动空间为D={a0,a1},其中a0表示接受H0,a1表示拒绝H0。
设参数θ的先验分布为H(θ),则δ(x)的Bayes风险为
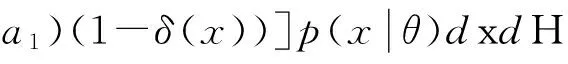
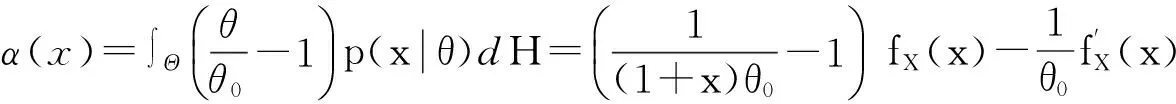
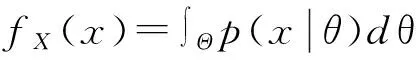
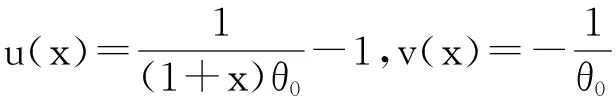
设随机变量序列{X1,X2,…,Xn,X}是同分布NA的,其中X1,X2,…,Xn是历史样本,X是当前样本。参数θ的先验分布为π(x)。本文假定:
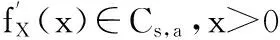
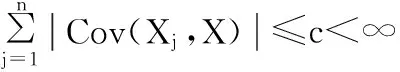
(c)对于Borel可测函数ki(·),在(0,1)外为零, (0,1)内有界的,i=0,1。并且满足条件:
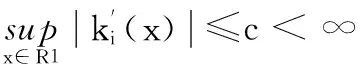
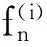
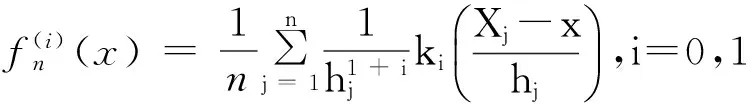
递归核估计方法是Wolverton和Wagner在1969年提出的,它改进了1956年Rosenblatt提出的核估计方法。一方面递归核估计的递归性质,大大减少了估计密度函数的计算量;另一方面,其可变窗宽的特点克服了估计的过度平滑和锐化,能够较固定窗宽更细致地刻画密度函数,从而提高估计效率。
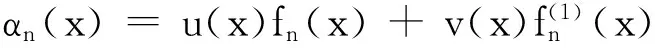
则δn(x)的全面风险函数为

En表示对X1,X2,…,Xn联合分布求期望。
为获得经验Bayes检验函数{δn(x)}的渐近最优性和收敛速度的阶,在此引入下述定理。下文M,M1,M2表示正常数,在不同式子中表示不同的值,即使在同一表达式中也如此。h,H分别表示最小窗宽和最大窗宽。
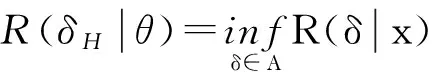
(1)
(2)

引理2[8]设X和Y是NA随机变量且方差有限,则对于任何可微函数g1(x),g2(x)有
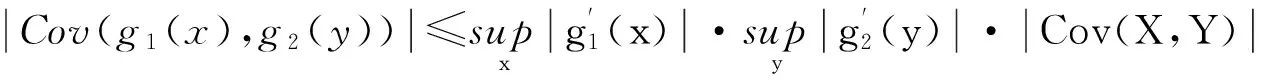
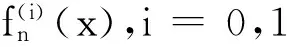
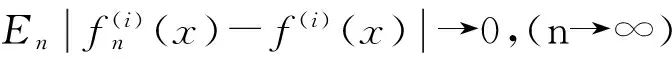
2主要结果及证明
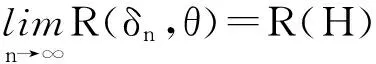
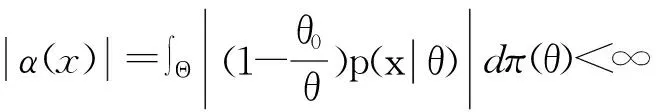
由引理1和控制收敛定理有,
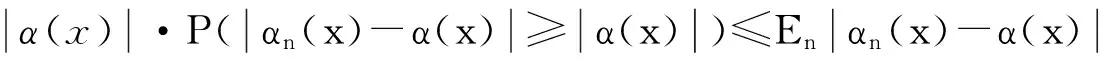
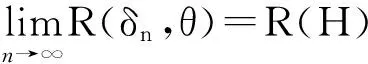
即经验Bayes检验函数{δn(x)}是渐近最优的。
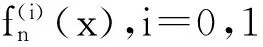
证明由引理1和Markov不等式得


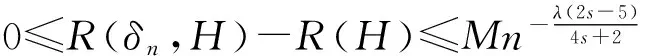
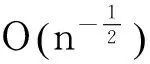
(对于PA随机变量序列也可运用本文的方法证明经验Bayes检验函数的渐近最优性,获得经验Bayes检验函数的收敛速度。)
参考文献:
[1] GHITANY M E,ATIEH B,NADARAJAH S.Lindley Distribution and its Applications[J].Mathematics and Computers in Simulation,2008,78(4):493-506.
[2] 杜伟娟,彭家龙,李体政.Lindley分布参数的经验Bayes检验的收敛速度[J].统计与决策,2012(21):23-26.
[3] 龙兵.Lindley分布中参数的区间估计和假设检验[J].广西民族大学(自然科学版),2014,20(1):59-62.
[4] JOAG D K,PROSCHAN F.Negative association of random variables with application[J].Ann Statist,1983,11(1):286-295.
[5] LINDLEY D V.Fiducial Distributions and Bayes’ Theorem[J].Journal of the Royal Statistical Society,Series B,1958,20(1):102-107.
[6] WOLVERTON C T,WAGNER T J. symptotically Optimal Discriminant Functions for Pattern Classification[J].IEEE Trans Inform Th,1969,15(2):258-265.
[7] JOHNS M V J,VAN R J.Convergence Rates in Empirical Bayes Two-action Problems Ⅱ.Discrete Case[J].Ann Math Statist,1972,43(3): 934-947.
[8] PAN J M.On the Convergence Rates in the Central Limit Theorem for Negatively Associated Sequences[J].Chinese Journal of Appl Prob And Star,1997,13(2):183-192.
[9] 王亮,师义民.NA样本下一类指数分布族的经验贝叶斯检验[J].西北大学学报(自然科学版),2008,38(4):523-526.
The empirical Bayes test problem for Lindley under NA sample
FAN Zimiao,ZHOU Juling*
(Department of Mathematical sciences, Xinjiang normal university, Urumqi, Xinjiang 830017, China)
Abstract:Under the NA sample, the problem was discussed that the empirical Bayes test problem for lindley. Results: the test function was created by using the kemel estimation with variable window width of density function. The empirical Bayes test function is obtained, and asymptotic optimality is proved , and convergence rates is get on suitable conditions.
Key words:NA sample; Lindley distribution; the empirical Bayes test
文章编号:1004—5570(2016)02-0068-03
收稿日期:2015-12-09
作者简介:范梓淼(1991-),女,在读硕士,研究方向:概率论与数理统计,E-mail:1421237334@qq.com. *通讯作者:周菊玲(1968-),女,副教授,研究方向:概率论与数理统计,E-mail:326815649@qq.com.
中图分类号:O212.1
文献标识码:A

