一类无限维Cartan型Lie代数的Witt子代数与模

姚廷富,施妮沙,吴宗显,戴先胜

(1.贵阳学院 数学与信息科学学院,贵州 贵阳　550005;2.贵州师范大学 数学与计算机科学学院,贵州 贵阳　550001)

一类无限维Cartan型Lie代数的Witt子代数与模

姚廷富1,施妮沙1,吴宗显1,戴先胜2*

(1.贵阳学院 数学与信息科学学院,贵州 贵阳550005;2.贵州师范大学 数学与计算机科学学院,贵州 贵阳550001)

摘要：主要讨论了与Witt代数相关的一类无限维Cartan型Lie代数G的结构，同时通过构造法给出它的一类Witt子代数与一类模。

关键词：无限维李代数；Witt子代数；模

0引言

Lie代数相关理论源于对李群的探讨与研究，目前已经成为代数学及其相关研究方向的一个主要内容.Witt代数是一类重要的无限维的Lie代数，Lie代数的一些相关基本知识见文献[1]。研究一个Lie代数的结构及其子代数，讨论其表示即模，是Lie代数的主要研究课题，非常有意义。文献[2]研究了广义Witt代数V=L(dα;α∈Q)的子结构。文献[3]研究与W代数相关联的几类无限维Lie代数的结构和表示。本文讨论了与Witt代数相关的一类无限维Cartan型Lie代数G的结构，同时给出它的一类Witt子代数与一类模，本文的结果对丰富无限维Lie代数及其表示理论具有重要意义,而且为研究无限维Lie代数G的子代数的性质以及模的性质奠定了一定的基础。

1基本知识

定义1.1[1]设L为域F上的向量空间，具有括积运算L×L→L,记为(x,y)|→[x,y],如果以下条件(L1)(L2)(L3)被满足，则称L为域F上的Lie代数。

(L1)括积运算是双线性的；

(L2)[x,x]=0(∀x∈L);

(L3)[x,[y,z]]+[y,[z,x]]+[z,[x,y]]=0(∀x,y,z∈L)。(L3)称为Jacobi等式.

定义1.2[1]设L为域F上的Lie代数,V为域F上的向量空间,V被赋予一个运算L×V→V(记为(x,v)|→x·v)后，如果以下条件(M1)(M2)(M3)成立，则V被称为域F上的一个L-模。

(M1)(ax+by)·v=a(x·v)+b(y·v);

(M2)x·(av+bw)=a(x·v)+b(x·w);

(∀x,y∈L；∀v,w∈V；∀a,b∈F)。

2Lie代数(G，[,])的Witt子代数

2.1Lie代数(G，[,])的结构

显然G成为一个线性空间。

定理2.1设G为定义2.1所述，括积运算如下，

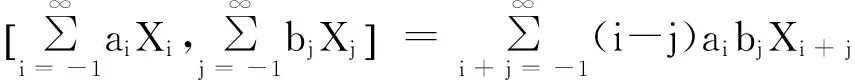
事实上，

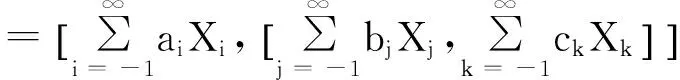
2.2Lie代数(G，[,])的Witt子代数

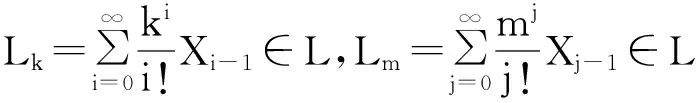
于是

=(k-m)Lk+m∈L。

[Lk，Lm]=(k-m)Lk+m

具有Witt代数括积运算特征，因此L=(L，[，])成为上的Lie代数(G，[，])的Witt子代数.证毕.

3Lie代数(G，[,])的模

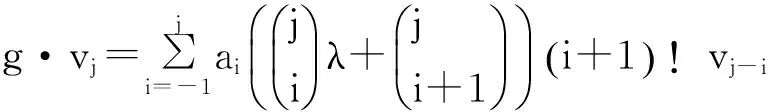
则V必定一个G-模。

=αg·vk+βh·vk。

2)g·(αvk+βvt)=αg·vk+βg·vk显然成立，因为G,V均为线性空间。

3)需要证[g,h]·vk=g·h·vk-h·g·vk成立。事实上，

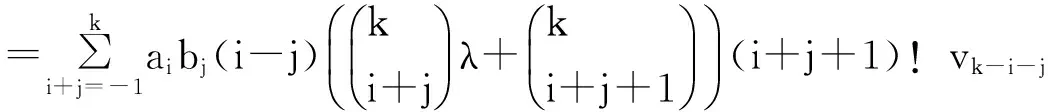
右边=g·h·vk-h·g·vk

经计算得，

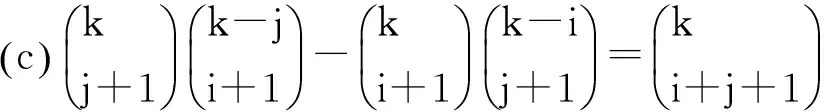
所以右边=

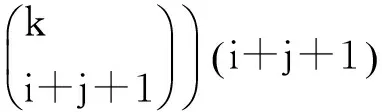
故左边=右边。证毕。

参考文献：

[1] 苏育才,卢才辉,催一敏.有限维半单李代数简明教程[M].北京：科学出版社，2008.

[2] 周敏，王宪栋，张燕燕.一类无限维李代数的子结构和性质[J].青岛大学学报(自然科学版),2013，26(4):32-35.

[3] 姚廷富，于亚峰，辛斌.非有限阶化无中心的超Virasoro代数[J].贵州师范大学学报(自然科学版),2010，28(1)：100-103.

[4]YANGHY,YUYF,YAOTF.DerivationalgebraandautomorphismgroupofgeneralizedtopologicalN =2superconformalalgebra[J].FrontMathChina,2013,8(4):973-986.

[5]YANGHY,YAOTF,YUYF.LieSuper-bialgebraStructuresonGeneralizedRamondN =2Super-VirasoroAlgebras[J].AlgebraColloquium,2013,20(2)：269-284.

[6] 戴先胜，辛斌.与Virasoro代数密切相关的非有限分次李代数的导子[J].贵州师范大学学报(自然科学版)，2011,29(4)50-53.

[7]SUYC.SimplemodulesoverthehighrankVirasoroalgebras[J].JCommAlgebra,2001,29:2067-2080.

[8]SUYC，XIAOQY.Classificationof2-gradedmodulesofintermediateseriesoveraBlock-typeLiealgebra[J].CommunicationsinContemporaryMathematics,2015,17(5):20-34.

Witt sub-algebras and modules of a class infinite dimensional Cartan type Lie algebras

YAO Tingfu1，SHI Nisha1，WU Zongxian1，DAI Xiansheng2*

(1.College of Mathematics and Information Science, Guiyang University, Guiyang ,Guizhou 550005;2.College of Mathematics and Computer Science, Guizhou Normal University, Guiyang ,Guizhou 550001)

Abstract:In this paper,the structures of a class infinite dimensional Cartan type Lie algebra relate to Witt algebra are mainly discussed. In accordance with structured approach,it given a class Witt sub-algebra and some modules of the Lie algebra.

Key words:infinite dimensional Lie Algebra;Witt sub-algebra;module

文章编号：1004—5570(2016)02-0064-04

收稿日期：2016-02-20

基金项目：贵州省科学技术基金项目(黔科合J字LKG[2013]31号；黔科合J字LKG[2013]30号)；贵阳学院重点课程建设项目(离散数学)；贵阳学院教学团队建设项目(数学建模教学团队；应用数学教学团队)

作者简介：姚廷富(1984-)，男，讲师、硕士，研究方向：李代数及其表示，数据分析，E-mail:ytfwdm520@163.com. *通讯作者：戴先胜(1977-)，男,讲师、在读博士，研究方向：李理论，E-mail:daisheng158@126.com.

中图分类号：O152.7

文献标识码：A