关于欧拉方程φ(mn)=2×3(φ(m)+φ(n))的正整数解
郭 瑞,赵西卿,张利霞,许宏鑫
(延安大学数学与计算机科学学院,陕西 延安 716000)
关于欧拉方程φ(mn)=2×3(φ(m)+φ(n))的正整数解
郭瑞,赵西卿,张利霞,许宏鑫
(延安大学数学与计算机科学学院,陕西 延安716000)
摘要:基于φ(n)为Euler函数,探讨了不定方程φ(mn)=2×3(φ(m)+φ(n))的正整数解的问题,并利用初等解法给出了该方程满足m≤n的所有正整数解。
关键词:Euler函数;正整数解;不定方程;初等解法
0引言
对于任意的正整数n,Euler函数φ(n)定义为序列1,2,…,n-1中与n互素的整数的个数。 Euler函数是数论中的一个重要函数,关于它的一些重要性质及与之有关的不定方程的正整数解,目前仍是一个重要的问题。Euler函数是一类重要的积性函数,文献[1]中,对于任意的正整数m,n,当(m,n)=1时,有φ(mn)=φ(m)φ(n)。文献[2]和[3]中研究了欧拉函数的可加性问题。1960年,Makowski Andrzej在文献[4]中讨论了不定方程φ(mn)=φ(m)+φ(n)的正整数解的问题。 2010年,孙翠芳等在文献[5]中讨论了方程φ(mn)=k(φ(m)+φ(n))的可解性并获得该方程的部分正整数解,其中k为素数。2014年,张四保等[6],在文献[5]的基础上给出方程φ(mn)=k(φ(m)+φ(n))当k=3时的所有35组解,并讨论了对任意奇数k,当k>3时方程的解的情况。文献[7,8]分别讨论了k=2,4时方程φ(xyz)=k(φ(x)+φ(y)+φ(z))的解的问题。本文将研究方程φ(mn)=2×3(φ(m)+φ(n))的可解性问题。
1预备知识
引理1[1]若p为素数,则φ(p)=p-1。
引理2[1]若p为素数,且α≥1,则φ(pα)=pα-pα-1=pα-1(p-1)。
引理3[1]对任意的正整数m,n,若m|n,则φ(m)|φ(n)。
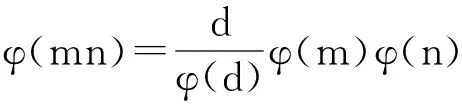
引理5[1]对任意的正整数m,n,若m>2,则2|φ(m)。
引理6Ⅰ)方程φ(x)=2的解为x=3,4,6;Ⅱ)方程φ(x)=4的解为x=5,8,10,12;Ⅲ)方程φ(x)=8的解为x=15,16,20,24,30;Ⅳ)方程φ(x)=16得解为x=17,32,34,40,48,60。
证明我们只证明φ(x)=4的情形,其他情形类似可得。 令x=2α13α25α3,其中α1,α2,α3为正整数,则由引理2得
φ(x)=φ(2α13α25α3)=2α1-1·2·3α2-1·4·5α3-1
ⅰ)当α1≠0,α2=α3=0时,有φ(x)=φ(2α1)=2α1-1=4,则α1=3,x=8。
ⅱ)当α2≠0,α1=α3=0时,有φ(x)=φ(3α2)=3α2-1=2·3α2-1=4,无解。
ⅲ)当α3≠0,α1=α2=0时,有φ(x)=φ(5α3)=5α3-1=4·5α3-1=4,则α1=1,x=5。
ⅳ)当α1,α2≠0,α3=0时,有φ(x)=φ(2α13α2)=2α1-1·2·3α2-1=4,则α1=2,α2=1,x=12。
ⅴ)当α1,α3≠0,α2=0时,有φ(x)=φ(2α15α3)=2α1-14·5α3-1=4,则α1=α3=1,x=10。
ⅵ)当α2,α3≠0,α1=0时,有φ(x)=φ(3α25α3)=2·3α2-14·5α3-1=4,无解。
ⅶ)当α1,α2,α3≠0时,有φ(x)=φ(2α13α25α3)=2α1-12·3α2-14·5α3-1=4,无解。
引理7Ⅰ)若φ(x)=6,则x=7,9,14,18;Ⅱ)若φ(x)=12,则x=13,21,26,28,36,42;Ⅲ)当φ(x)=18,则x=19,27,38,54;Ⅳ)若φ(x)=24,x=35,39,45,52,56,70,72,78,90;Ⅴ)若φ(x)=36,则x=37,57,63,74,76,108,114,126。
证明同引理6可得。
2主要结果
定理1不定方程φ(mn)=2×3(φ(m)+φ(n))满足m≤n的所有正整数解为(15,52);(15,56);(16,35);(16,39);(16,45);(20,39);(24,35);(13,21);(13,28);(13,36);(13,42);(21,26);(8,26);(8,42);(10,26);(10,28);(10,36);(10,42);(12,26);(14,18);(9,21);(9,42);(18,21);(15,24);(8,28);(8,36);(12,28);(7,63);(7,126);(14,63);(9,36);(12,12)。
证明令(m,n)=d,则有d|m,d|n由引理3得
φ(d)|φ(m),φ(d)|φ(n)
即存在a,b∈Z+使得
φ(m)=aφ(d),φ(n)=bφ(d)
由引理4得
又
φ(mn)=6(φ(m)+φ(n))=6(aφ(d)+bφ(d))
即有
下面对d进行分类讨论,不妨设a≤b。
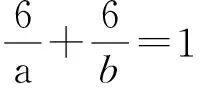
从而有
a=7,b=42;a=8,b=24;a=9,b=18;a=10,b=15或a=12,b=12
又
φ(d)=1
所以
φ(m)=7,φ(n)=42;φ(m)=8,φ(n)=24;φ(m)=9,φ(n)=18;φ(m)=10,φ(n)=15
或φ(m)=12,φ(n)=12。
若
φ(m)=7,φ(n)=42,
由引理5得,方程无正整数解。
若
φ(m)=8,φ(n)=24,
则有
(m,n)=(15,32);(15,56);(16,35);(16,39);(16,45);(20,39);(24,35)。
若
φ(m)=9,φ(n)=18,
由引理5得,方程无正整数解。
若
φ(m)=10,φ(n)=15,
由引理5得,方程无正整数解。
若
φ(m)=12,φ(n)=12,
则有
(m,n)=(13,21);(13,28);(13,36);(13,42);(21,26)。
从而有
a=4,b=12;或a=6,b=6。
又
φ(d)=1,
所以
φ(m)=4,φ(n)=12或φ(m)=6,φ(n)=6。
若
φ(m)=4,φ(n)=12,
则有
(m,n)=(8,26);(8,42);(10,26);(10,28);(10,36);(10,42);(12,26)。
若
φ(m)=6,φ(n)=6,
则有
(m,n)=(14,18)。
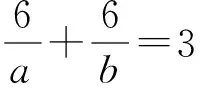
从而有
a=3,b=6或a=4,b=4。
又
φ(d)=2,
所以
φ(m)=6,φ(n)=12或φ(m)=8,φ(n)=8。
若
φ(m)=6,φ(n)=12,
则有
(m,n)= (9,21);(9,42);(18,21)。
若
φ(m)=8,φ(n)=8,
则有
(m,n)=(15,24)。
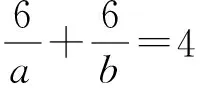
从而有
a=2,b=6或a=3,b=3。
又
φ(d)=2,
所以
φ(m)=4,φ(n)=12或φ(m)=6,φ(n)=6。
若
φ(m)=4,φ(n)=12
则有
(m,n)=(8,28);(8,36);(12,28)。
若φ(m)=6,φ(n)=6,与(m,n)=4矛盾,所以方程无正整数解。
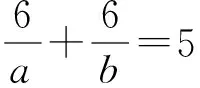

从而有
a=2,b=2。
又
φ(d)=2,
所以
φ(m)=4,φ(n)=4。
当φ(m)=4,φ(n)=4时,与(m,n)=6矛盾,所以方程无正整数解。
从而有
a=1,b=6。
又
φ(d)=6,
所以
φ(m)=6,φ(n)=36,
则有
(m,n)=(7,63);(14,63);(7,126)。
从而有
a=1,b=3。
又
φ(d)=4,
所以
φ(m)=4,φ(n)=12,
当φ(m)=4,φ(n)=12时,与(m,n)=8矛盾,所以方程无正整数解。
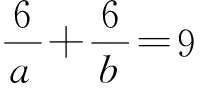
从而有
a=1,b=2。
又
φ(d)=6,
所以
φ(m)=6,φ(n)=12。
当
φ(m)=6,φ(n)=12,
则有
(m,n)=(9,36)。
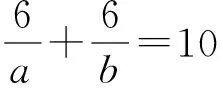
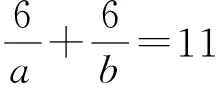
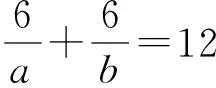
从而有
a=1,b=1。
又
φ(d)=4,
所以
φ(m)=4,φ(n)=4。
则有
(m,n)=(12,12)。
通过以上讨论,可得不定方程φ(mn)=2×3(φ(m)+φ(n))满足m≤n的所有正整数解为(15,52);(15,56);(16,35);(16,39);(16,45);(20,39);(24,35);(13,21);(13,28);(13,36);(13,42);(21,26);(8,26);(8,42);(10,26);(10,28);(10,36);(10,42);(12,26);(14,18);(9,21);(9,42);(18,21);(15,24);(8,28);(8,36);(12,28);(7,63);(7,126);(14,63);(9,36);(12,12)。
参考文献:
[1]ROSENKH.ElementaryTheoryandItsApplications[M].AddisonWesley:Fifthedition,PearsonEducation,Inc,2005.
[2]GUYRK.UnsolverdProblemsinNumberTheory[M].Thirdedition,Beijing;SciencePress,2004.
[3] 左可正.欧拉函数不定方程的可解性探讨[J].黄石理工学院学报,2008,24(2):49-52.
[4]MAKOWSKA.OnSomeEquationsInvolvingFunctinosand[J].MathMonthly,1960,67:668-670.
[5]SUNCF,CHENGZ.SomekindofequationinvolvingEulerfunction[J].JournalofMathematicalStudy,2010,43(4):364-369.
[6] 张四保.有关Euler函数φ(n)的方程的正整数解[J].数学实践与认识, 2014,44(20):302-305.
[7] 张四保.关于方程φ(xyz)=4(φ(x)+φ(y)+φ(z))[J].东北石油大学学报,2013,37(6):113-118.
[8] 史保怀,潘晓玮. 关于数论函数方程φ(x1…xn-1xn)=(φ(x1)+…φ(xn-1)+φ(xn))[J].数学实践与认识,2012,42(23):267-271.
[9] 姜友谊.关于欧拉函数φ(x)=m的解[J].重庆工业管理学院学报,1998,12(5):91-94.
[11]田辰亮,付静,白维祖.一个包含欧拉函数的方程[J].纯粹数学与应用数学,2010,26(1):96-98.
The positive integer solutions of Euler functionφ(mn)=2×3(φ(m)+φ(n))
GUO Rui,ZHAO Xiqing,ZHANG Lixia,XU Hongxing
(College of Mathematics and Computer Science,Yan’an University,Yan’an, Shaanxi 716000,China)
Abstract:Based on φ(n) be Euler function, discussed the positive integer solutions of Diophantine equation φ(mn)=2×3(φ(m)+φ(n)).We give all positive integer solutions by using elementary methods which satisfy m≤n.
Key words:Euler function; positive integer solutions; diophantine equation; elementary methods
文章编号:1004—5570(2016)02-0060-04
收稿日期:2016-01-18
基金项目:陕西省教育厅科研计划资助项目(2013JK0557);2013延安大学自然科学专项基金资助项目(YD2013-05);延安大学研究生教育创新计划项目
作者简介:郭瑞(1990-),女,在读研究生,研究方向:数论,E-mail:744910359@qq.com. *通讯作者:赵西卿(1965-),男,副教授,硕士生导师,研究方向:解析数论,E-mail:ydzhaoxiqing@126.com
中图分类号:O156
文献标识码:A

