基于并行DBSCAN算法的数字调制信号识别
赵知劲,顾嘉伟
(杭州电子科技大学通信工程学院,浙江 杭州 310018)
基于并行DBSCAN算法的数字调制信号识别
赵知劲,顾嘉伟
(杭州电子科技大学通信工程学院,浙江 杭州 310018)
摘要:利用四阶、六阶和八阶累积量提取2个特征参数识别2ASK,4ASK,QPSK,8PSK,MFSK和16QAM,有效抑制高斯白噪声的影响.利用改进后的并行DBSCAN算法对特征参数集进行聚类,根据高密度簇中心点与特征参数理论值的距离识别该簇的调制方式,再将未归成簇的数据归于最近的聚类簇中,完成所有数据的识别.仿真结果表明,改进后的并行DBSCAN算法能有效提高聚类效率;信噪比大于4 dB时,所提出的二个特征参数能够达到98%以上的信号识别正确率.
关键词:高阶累积量;调制识别;并行;DBSCAN算法
0引言
调制样式识别是无线电资源管理、电子侦察等领域的重要环节,其包括2个关键技术,分别为特征参数提取和分类识别方法,国内外学者对此进行了大量研究.在多路并行接收条件下,接收机在接收大量信号的同时,从大量数据中提取到有效的、受噪声影响小的特征参数,并进行高性能的识别非常关键.高阶累积量对高斯白噪声抑制能力强[1].文献[2]从四阶、六阶累积量中提取2个特征参数,识别了2ASK,4ASK,QPSK,MFSK和16QAM信号;文献[3]从二阶与四阶累积量中提取3个特征参数,识别了2ASK,4ASK,QPSK和MFSK信号;文献[4]从二阶与八阶累积量中提取1个特征参数,识别了2ASK,4ASK,8ASK,QPSK,8PSK,MFSK和16QAM信号,但该特征参数受高斯白噪声的影响较大.对信号分类识别时,决策树[2-4]方法需要确定合适的判决门限,BP神经网络[5-7]等方法需要大量合适的训练集.基于密度的聚类(Density-Based Spatial Clustering of Applications with Noise,DBSCAN)算法是一种基于密度的无监督聚类算法,将高密度的区域划分成簇,得到任意形状的簇,将其用于调制识别无需训练数据.但DBSCAN算法的复杂度为O(λ2),聚类效率受数据个数λ影响较大.FDBSCAN(Fast DBSCAN)[8]和IF-DBSCAN(Improved FDBSCAN)[9]选取种子对象进行扩展,减少扩展次数,HDBSCAN(Based Hierarchy DBSCAN)[10]利用共享点实现簇合并,以提高聚类效率,但这些算法都会生成小类.基于网格的DBSCAN[11-12]优化了区域查询操作,减少了扩展时的复杂度.文献[13-14]提出了基于数据交叠分区的并行DBSCAN算法,其基于网格的划分方式容易产生较多边界数据.
本文从四阶、六阶和八阶累积量中提取2个特征参数,对并行接收和提取的信号特征参数构成的数据集进行交叠分区,提出利用粒子群(Particle Swarm Optimization, PSO)算法搜寻数据集最优划分边界的划分方式,改进并且并行实现DBSCAN算法,最后得到基于并行DBSCAN的2ASK,4ASK,QPSK,8PSK,MFSK和16QAM信号的调制样式识别算法.
1数字调制信号的特征参数
1.1信号模型
在载波频率、相位、定时同步的前提下,下变频后数字调制基带信号的复数形式为:

(1)
其中,N为码元长度,aL为码元序列,A为信号能量,G(t)为码元波形,Ts为码元宽度,θc为载波相位差,n(t)为零均值的高斯白噪声.不同调制方式M进制的aL分别表示为:

2)MPSK信号:aL∈{ej2π(r-1)/M,r=1,2,…,M};
3)MFSK信号:aL=ej2πfLt,fL∈{(2r-1-M)Δf,r=1,2…M},Δf为信号频偏;
1.2特征参数选取
平稳随机信号x(t)的K阶累积量定义为
CKv(x(t))=Cum(X).
(2)
其K阶混合矩定义为
MKv=E[x(t)K-vx*(t)v].
(3)
其中,x*(t)为x(t)的共轭,高阶累积量可以用高阶矩表示:

(4)
假设信号为x(t)=S(t)+n(t),其中S(t)为有用信号,与n(t)相互独立.根据统计量理论可知,零均值的高斯白噪声二阶以上累积量恒为0,因此当K>2时,由高阶累积量的性质有
CKv(x(t))=CKv(S(t))+CKv(n(t))=CKv(S(t)).
(5)
所以,采用高阶累积量识别信号可以有效避免高斯白噪声的影响.2ASK,4ASK,QPSK,8PSK,MFSK和16QAM信号的各阶累积量理论值如表1所示,A为信号能量.由表1可见,信号的累积量与接收信号能量A有关,在提取特征参数时需要消除能量的影响.文献[3-4]采用各阶累积量与C21的比值作为特征参数,虽然能够消除能量带来的影响,但是高斯白噪声的C21并不为0,因此该特征参数受高斯白噪声影响大.

表1 调制信号的高阶累积量理论值
本文提取以下2个特征参数用于识别这6种信号:

(6)

(7)
其理论值如表2所示.虽然理论上TZ1可以区分这6种信号,但实际中,16QAM信号样本与QPSK信号样本的TZ1值受噪声影响大而比较接近,区分并不明显.而16QAM信号样本与QPSK信号样本的TZ2值受噪声影响较小,因此利用TZ1和TZ2以提高两者的区分度.

表2 调制信号的特征参数理论值
2基于Hadoop实现的并行DBSCAN算法的调制信号识别
对并行接收到的信号提取λ组特征参数(TZ1,TZ2),从而得到特征参数数据集.DBSCAN算法对数据集进行聚类,获得形成高密度簇的数据和未形成高密度簇的数据.计算高密度簇的中心点与(TZ1,TZ2)理论值的距离,距离最小的理论值对应的调制方式就是该高密度簇的识别结果,最后将未归成簇的数据归到最靠近它的高密度簇中完成所有数据的调制识别.
2.1DBSCAN聚类算法的改进
首先给出DBSCAN算法涉及到的一些定义:
1)点o的Eps邻域:与点o的距离小于Eps的区域;
2)核心点:点o的Eps邻域中包含点数大于等于Minpts,则o为核心点,其中Minpts为自定义的阈值;
3)直接密度可达:核心点o的Eps邻域内包含点q,则称q到o直接密度可达;
4)密度可达:存在一系列的点o1,…,om,o1=q,om=o,且oi+1到oi是直接密度可达,则称o到q密度可达.
传统DBSCAN算法的计算开销主要来源于两个方面:所有点的扩展和扩展时的计算.本文对每一数据块的DBSCAN聚类采用粗聚类和粗聚类簇合并两阶段实现,降低其计算复杂度.
第一阶段:粗聚类.流程如图1所示.先选取数据集中的任意点q1,检测其是否为核心点,如果是核心点,则q1与其Eps邻域内所有点形成1个粗聚类簇,簇中所有点赋予相同簇标识,并将q1标记为该簇的核心中心点.再从数据集中选取没有簇标识的任意点q2,利用没有簇标识的点判断其是否为核心点,如果是核心点进行上述同样的操作,如果不是则选取下1个对象.重复上述操作,直到没有簇标识的点不再具有核心点后,这些点各自成1簇,且该点为该簇的非核心中心点.
第二阶段:粗聚类簇合并.流程如图2所示.设点a、点b分别为簇A、簇B的中心点,簇A中的点的邻域包含簇B中的点需要满足如下距离规则:1)点a为核心中心点时,如果点b为核心中心点,则点a与点b的距离须小于3Eps,如果点b为非核心中心点,则点a与点b的距离须小于2Eps;2)点a为非核心中心点时,如果点b为核心中心点,则点a与点b的距离须小于2Eps,如果点b为非核心中心点,则点a与点b的距离须小于Eps.在只扩展簇A和簇B点的前提下,判断点a与点b是否密度可达.如果密度可达,则两簇合并.为了准确判断数据点是否为核心点,需要将满足上述距离规则的所有簇都加进来计算,但无需对它们扩展.一旦实现了簇A与簇B的合并,那么后续的点就不用扩展了,因此整个数据集中,只有部分点进行了扩展,降低了计算复杂度.

图1 第一阶段流程图

图2 第二阶段流程图
2.2基于PSO算法的数据划分
数据交叠分区是并行DBSCAN算法基础,其基本思想是:假设x为划分边界,边界区域为x±Eps.处于边界区域中的数据点在相邻数据块中被重复.由此可见,理想的划分边界应该满足:1)处于边界区域的点数尽可能少;2)划分后的各数据块点数不会非常少.文献[13-14]提出的划分方式中,其网格分布是固定的,不够灵活,容易产生较多边界数据.
划分边界的优化目标如下:
min{g(x)=card(D)}.
(8)
其中,D为处于边界区域中的数据点集合,card(D)表示D集合中的元素个数.约束条件为:
∀card(IZ)>Y,
(9)
其中,IZ为划分后第Z个数据块中的数据点集合,Y为事先设定的数据块最小点数.
基于上述优化目标和约束条件,本文采用PSO算法搜索这样的划分边界,每进行1次搜索获得1个划分边界,直到所有的数据块点数满足要求搜索结束.假设数据的维度为h,每1维变量为连续量,第i个粒子的位置pi结构如图3所示.

pi(1)pi(2)…pi(h)
图3粒子pi的结构
其中,pi(W)对应第W维的划分边界.所有粒子通过2个最优值来更新自己的位置,1个是自身在迭代过程中搜索到的个体最优解,另1个是所有粒子搜索到的全局最优解.粒子群初始化过程是:在数据集中随机选取s个点,将第i个数据点的坐标值赋给第i个粒子pi(1≤i≤s).粒子群算法第k次迭代的更新公式如下:

(10)

(11)
其中,vi和pbi分别表示第i个粒子的速度矢量和个体最优解,w是惯性权重,gb是全局最优解,gf为gb的适应度值,R是介于0到1之间随机数,C1和C2是学习因子.
根据式(8)和式(9),适应度值按如下公式计算:
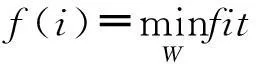
(12)
其中,f(i)表示pi的适应度值,fit(i,W)表示pi(W)的适应度值.
fit(i,W)=fit1+fit2.
(13)
其中,fit1是落在边界区域中的点数;如果划分后的数据块满足式(9),则fit2=0,否则fit2=CN,CN为一个较大的常数.全局最优解gb按如下公式进行更新.对于1≤W≤h,计算

(14)

(15)
如果满足条件gf(W)>bfW,则gb(W)=piW(W),gf(W)=bfW,gf(W)为gb(W)的适应度值.当PSO算法搜索完毕后,计算gf中的最小值所在的位置
B=argmin{gf(W)}.
(16)
B为划分边界所在的维度,划分边界即为gb(B).如果在搜索过程中,gb(W)的适应度值等于0,表示边界区域不存在数据点且满足式(9),则认为是最优划分,直接跳出循环.
2.3并行DBSCAN算法的MapReduce实现
数据集经过PSO算法划分成多个数据块后,每个数据块可以独立地进行DBSCAN聚类.MapReduce[15]是一种并行编程模型,每个数据块的DBSCAN聚类由Map函数和Reduce函数完成.Map函数实现粗聚类:Map函数的输入为1个数据块,
3仿真实验
本节分析比较应用本文DBSCAN算法、传统DBSCAN、FDBSCAN[8]、HDBSCAN[10]和基于网格的DBSCAN[11-12]识别2ASK,4ASK,QPSK,8PSK,MFSK和16QAM信号性能.在虚拟机上搭建Hadoop平台,所用操作系统是Ubuntu,Hadoop版本为0.20.2,Java版本为jdk1.6.0_24.信号的载波频率为10kHz,采样频率为60kHz,码元速率为1 000baud,计算每个特征参数所需的码元个数为3 000,FSK信号的频偏为5kHz.数据集大小为λ,划分后数据块大小介于λ的15%~20%之间.
本文提出的基于PSO划分方式与基于网格[13-14]划分方式的边界区域中的重复数据点数对比如图4所示.由图4可见,本文划分方式产生的重复数据个数小于基于网格的划分方式,数据集越大,优势越明显,这表明PSO算法搜索到的划分边界更合理.
PSO算法交叠划分数据集后,采用本文并行实现的DBSCAN算法,DBSCAN,FDBSCAN,HDBSCAN和基于网格的DBSCAN聚类2ASK,4ASK,QPSK,8PSK,MFSK和16QAM信号特征参数所需时间如图5所示.由图5可见,本文算法所需的时间远小于DBSCAN,FDBSCAN和基于网格的DBSCAN,而略大于HDBSCAN,FDBSCAN和HDBSCAN算法的聚类结果会出现小类生成的问题,即无法保证聚类结果与DBSCAN算法一致.虽然整个数据集已经由PSO算法分成了多个块,但DBSCAN,FDBSCAN和基于网格的DBSCAN依旧需要消耗大量的时间,且随着数据集的增加,上升趋势非常快.而本文算法所需时间增加很缓慢,这是因为本文提出的聚类方式只有部分点需要进行扩展,而且在扩展时,只有部分数据参与计算,减少了大量的计算开销.

图5 聚类时间对比
加性高斯白噪声背景下,单独采用TZ1参数时,本文选择判决门限为65,50,33,15和0.55,进行如下判决:1)当TZ1≤0.55时,判断为MFSK信号;2)当0.55 表3 TZ1参数下,调制信号识别正确率 表4给出了使用TZ1参数和TZ2参数,本文方法识别上述6种信号的识别正确率;表5给出了参考文献的信号识别正确率,表5中“-”符号表示文献未给出此数据. 表4 TZ1和TZ2参数下,调制信号识别正确率 表5 本文参考文献方法下,调制信号识别正确率 对比表4和表5可见,本文方法的信号识别性能优于表5.信噪比为4dB时,除8PSK和MFSK外,本文方法对其余信号的识别正确率都达到了100%;信噪比为5dB时,本文方法对所有信号的识别正确率都达到了100%,而文献[2]和文献[4]方法均未能达到100%的识别正确率.文献[3]和文献[5]构造的BP神经网络分类器在8dB时,识别正确率才能够分别达到100%和95.2%以上,而且文献[3]需要3个特征参数.多路并行接收信号的信噪比为4~5dB之间时,本文方法对这6种信号的识别正确率仍可达到99%以上,这表明所提取的特征参数抗噪声能力强.相比于决策树、BP神经网络分类器,本文方法不需要设置门限,也不需要训练集. 4结束语 本文从四阶、六阶和八阶累积量中提取2个特征参数用于识别2ASK,4ASK,QPSK,8PSK,MFSK和16QAM信号,所提取的特征参数噪声鲁棒性强.利用改进的并行DBSCAN算法对特征参数进行聚类,根据特征参数理论值与聚类得到的高密度簇中心点的距离进行识别,最后将高密度簇外的数据归于最靠近的聚类簇中,完成所有数据的调制识别. 参考文献 [1]HANY,WEIG,SONGC,etal.Hierarchicaldigitalmodulationrecognitionbasedonhigher-ordercumulants[C]//InstrumentationMeasurementComputerCommunicationandControl(IMCCC),2012SecondInternationalConferenceon.Harbin:IEEE, 2012:1645-1648. [2]包锡锐,吴瑛,周欣.基于高阶累积量的数字调制信号识别算法[J].信息工程大学学报,2007,80(4):463-467. [3]张驰,吴瑛,周欣.基于高阶累积量的数字调制信号识别[J].数据采集与处理,2010,25(5):575-579. [4]郭娟娟,尹洪东,姜璐,等.利用高阶累积量实现数字调制信号的识别[J].通信技术,2014,47(11):1255-1260. [5]李敏.数字通信信号自动调制识别技术的研究[D].哈尔滨:哈尔滨工程大学,2012. [6]ADZHEMOVSS,TERESHONOKMV,CHIROVDS.Typerecognitionofthedigitalmodulationofradiosignalsusingneuralnetworks[J].MoscowUniversityPhysicsBulletin, 2015, 70(1):22-27. [7]KESHKEHM,El-NABYMA,AL-MAKHLASAWYRM,etal.Automaticmodulationrecognitioninwirelessmulti-carrierwirelesssystemswithcepstralfeatures[J].WirelessPersonalCommunications, 2014, 81(3):1-46. [8]周水庚,周傲英,曹晶,等.一种基于密度的快速聚类算法[J].计算机研究与发展,2000,37(11):1288-1292. [9]王桂芝,王广亮.改进的快速DBSCAN算法[J].计算机应用,2009,29(9):2505-2508. [10]郗洋.基于云计算的并行聚类算法研究[D].南京:南京邮电大学,2011. [11]刘淑芬,孟冬雪,王晓燕.基于网格单元的DBSCAN算法[J].吉林大学学报(工学版),2014,44(4):1135-1139. [12]张枫,邱保志.基于网格的高效DBSCAN算法[J].计算机工程与应用,2007,43(17):167-169. [13]宋明,刘宗田.基于数据交叠分区的并行DBSCAN算法[J].计算机应用研究,2004,21(7):17-20. [14]孙雨冰.基于MapReduce化的数据聚类算法研究、设计与应用[D].上海:华东理工大学,2012. [15]陆嘉恒.Hadoop实战[M].北京:机械工业出版社,2012:99-117. Recognition of Digital Modulation Signals Based on the Parallel DBSCAN Algorithm ZHAO Zhijin, GU Jiawei (SchoolofCommunicationEngineering,HangzhouDianziUniversity,HangzhouZhejiang310018,China) Abstract:Two feature parameters extracted from four-order, six-order and eight-order cumulants of signals are used to recognize 2ASK, 4ASK, QPSK, 8PSK, MFSK, 16QAM, which can suppress white Gaussian noise. The data sets of feature parameters are clustered by the improved parallel DBSCAN. The high-density clusters are recognized by the distances of their centers and the theoretical values of the feature parameters, then the feature parameters outside the clusters are put in the closest cluster to achieve the recognition of all the feature parameters. Simulation results show that the improved parallel DBSCAN is more efficient. When the SNR is higher than 4 dB, the recognition rates are higher than 98% by using the two proposed feature parameters. Key words:high-order cumulants; modulation recognition; parallel; DBSCAN algorithm DOI:10.13954/j.cnki.hdu.2016.02.001 收稿日期:2015-09-06 作者简介:赵知劲(1959-),女,浙江宁波人,教授,调制样式识别. 中图分类号:TN911.6 文献标识码:A 文章编号:1001-9146(2016)02-0001-07



