无缝钢管纵连轧无网格法热力耦合分析
周 研,双远华,赵春江,苟毓俊,刘邱祖
(太原科技大学 a.机械工程学院,b.材料科学与工程学院,c.太原重型机械装备协同创新中心,太原 030024)
无缝钢管纵连轧无网格法热力耦合分析
周研a,c,双远华b,c,赵春江b,c,苟毓俊b,c,刘邱祖a
(太原科技大学 a.机械工程学院,b.材料科学与工程学院,c.太原重型机械装备协同创新中心,太原 030024)
摘要:采用混合交换法修正无网格移动最小二乘近似函数,以便直接施加边界条件;采用伽辽金法构建速度场刚度矩阵;采用配点法构建温度场刚度矩阵;采用间接耦合法将速度场与温度场耦合求解;最终推导出了刚塑性无网格法热力耦合计算公式,实现了纵连轧过程的热力耦合模拟。通过数值模拟与实验研究对比表明,模拟结果与实验结果吻合度较高,充分验证了本文给出的无网格法的可靠性和正确性。
关键词:无缝钢管;纵连轧;无网格法;热力耦合分析
无网格法(Meshless Method)对求解域进行节点离散与节点近似,避免求解过程对网格的依赖,无需对网格进行划分或重构,保证计算精度的同时减小了计算难度[1-2],在工程数值模拟应用中越来越受到人们的重视。国内外许多学者均在尝试使用无网格方法解决金属塑性成形问题。最早,由美国学者CHEN et al将RKPM方法应用于金属环件延伸、冷墩粗和压缩过程问题的研究[3-4];赵国群等利用刚塑性材料假设,并对本质边界条件采用变换法处理,对典型墩粗过程进行了模拟[5];李光耀等利用RKPM 法对三维弹塑性金属材料的成形问题进行了模拟[6];孙杰等基于无网格径向点插值法(RPIM)与伽辽金法(EFG)对斜轧延伸过程进行了数值仿真[7]。
笔者采用混合交换法[8]修正无网格移动最小二乘近似函数,以便直接施加边界条件;采用伽辽金法构建速度场刚度矩阵,该算法稳定性好、分析精度高;采用配点法构建温度场刚度矩阵,以简化温度场刚度矩阵构建过程,并采用隐式Euler向后差分格式进行温度场时间域离散。在热力耦合分析中,采用间接耦合法[9],将速度场与温度场两个相对独立的子系统耦合求解;借助本构关系,将变形与传热相互影响同时考虑,最终推导出了刚塑性无网格法热力耦合分析公式,实现纵连轧过程的热力耦合分析。通过数值模拟与实验研究对比发现,模拟结果与实验结果吻合度较高,验证了本文给出的无网格法的可靠性和正确性。
1最小二乘近似与混合交换修正
求解域Ω内,一点x的速度u(x)的移动最小二乘近似(MLS)为
(1)
式中:uI为节点速度向量;u为广义速度向量;N为离散节点数目。MLS形函数矩阵为
由于MLS形函数在边界处不满足Kronecker delta条件,不能直接施加本质边界条件,需要进行修正,修正的方法有完全交换法[9]与局部交换法[8]。当节点数目较多时,使用完全交换法的计算工作量也随之增加。因此,笔者采用混合交换法对u进行局部修正,将N个离散节点分为NE个非约束节点和NB个约束节点,N=NE+NB。式(1)中,令x=xJ,LIJ=ΦI(xJ),得到
(2)
式中,I为单位矩阵。
(3)
式中:u*为经过混合交换后的速度向量;IE为NE×NE单位矩阵;Λ*为混合变换矩阵,
由式(3)可得
(4)
将式(4)代入式(2)得到局部修正的速度场函数向量
温度场向量也需采用同样的变换。
2连轧过程刚黏塑性无网格法
2.1速度场刚度矩阵的建立
基于刚黏塑性材料条件假设,应用不完全广义变分原理,采用罚函数引入体积不变条件,在局部坐标系下施加摩擦力边界条件,摩擦模型为反正切模型,真实解使系统能量速率泛函的一阶变分为零,即真实解满足如下刚度方程
(5)
式中:ΠD为应变能速率项;ΠP为引入体积不变条件的罚函数项;Πf为摩擦功率项。通过式(5)可以得到刚黏塑性无网格伽辽金法的速度场刚度方程
(6)
式中,α为惩罚因子。该方程为非线性方程,采用Newton-Raphson 迭代法对(6)式进行求解,直到获得收敛解。式(6)经过Newton-Raphson迭代,进行线性化处理后,并在局部坐标系下总装刚度方程,得到如下矩阵形式
(7)
2.2无网格热力耦合分析
假设材料导热各向同性,则节点xs瞬态温度应当满足如下平衡微分方程:
(8)
并且在给定初始条件后满足如下边界条件:
(9)

(10)
式中:T为某节点温度;h为工件与环境的总体换热系数;Ta为工件表面温度。工件接触表面由于摩擦产生的热通量为:
(11)
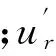
(12)
式中:hT为热交换系数;TT为工模具表面温度。将局部修正后的无网格形函数代入式(8)、(9)得到如下方程,
(13)
(14)
(15)
(16)
其中,lxs,mxs,nxs为接触点xs的外法矢方向余弦值,式(13)-(16)写成矩阵形式得
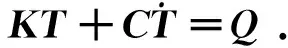
(17)
式中:
KT=[HT(x1),HT(x2),…,HT(xN),MT(x1),
MT(x2),…,MT(xNf),NT(x1),NT(x2),…,
NT(xNC),OT(x1),OT(x2),…,OT(xNC)];
CT=[CT(x1),CT(x2),…,CT(xN),0,…,0] ;
QT=[q(x1),q(x2),…,q(xN),hTa,hTa,…,
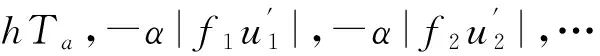
C(xs)=[-ρCΨ1(xs),-ρCΨ2(xs),…,
-ρCΨN(xs)] ;
H(xs)=[H1(xs),H2(xs),…,HN(xs)];
M(xs)=[M1(xs),M2(xs),…,MNf(xs)];
N(xs)=[N1(xs),N2(xs),…,NNc(xs)] ;
O(xs)=[O1(xs),O2(xs),…,ONc(xs)] ;
HI(xs)=kΨI,xx(xs)+kΨI,yy(xs)+kΨI,zz(xs) ;
MI(xs)=klxsΨI,x(xs)+kmxsΨI,y(xs)+
knxsΨI,z(xs)-hΨI(xs) ;
NI(xs)=klxsΨI,x(xs)+kmxsΨI,y(xs)+
knxsΨI,z(xs) ;
OI(xs)=klxsΨI,x(xs)+
kmxsΨI,y(xs)+knxsΨI,z(xs)-hTΨI(xs) .

(18)
取β=1,得到温度场刚度矩阵后,采用文献[10]提出的间接耦合迭代法即可得到稳定的温度场与速度场。具体实施步骤:先在每一个迭代步中首先计算节点温度场;再由所得温度场计算节点速度场;然后重复上两步,直到节点速度场与温度场同时收敛;最后更新节点坐标进行下一迭代步。
3钢管纵连轧过程热耦合分析
3.1纵连轧工艺及参数
管坯材料选用20#无缝钢管,不同温度不同等效应变率下的流变应力、应变曲线见图1所示。

a-2 s-1;b-20 s-1;c-200 s-1图1 不同应变率等效应力应变曲线Fig.1 Equivalent stress and strain curves under different strain rates
本次模拟与实验中设置纵连轧机架为3架,同一机架内轧辊互成120°角布置,并且相邻机架前后轧辊成60°角。其中,包含3组共9个轧辊,限动芯棒被插入中空的毛管中,并参与整个塑性变形过程如图2所示。

图2 纵连轧工艺几何模型Fig.2 Geometrical model of the longitudinal rolling process
3.2无网格分析参数
管坯取1/6模型进行分析,离散节点总数为31 156个,径向分5层排列,8个相邻节点构成一个背景积分网格;采用完全高斯积分,积分阶次2×2×2,基函数采用线性基函数,权函数选取三次样条函数。节点影响域为球体域,影响域系数选取2.5;时间步长为0.01s。管坯某部分无网格离散点模型如图3所示。
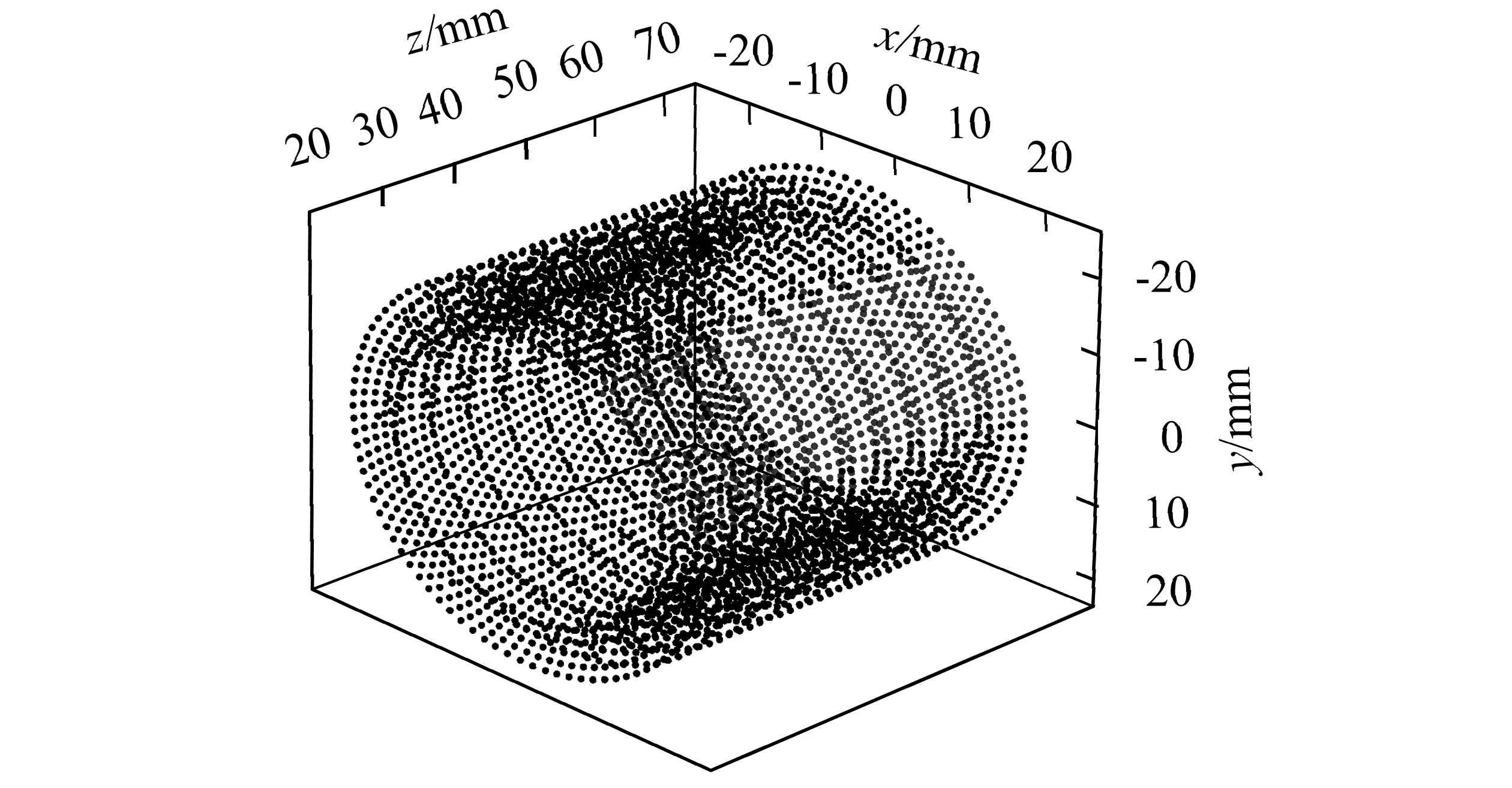
图3 无网格法节点图Fig.3 Node points in meshless method
3.3结果分析
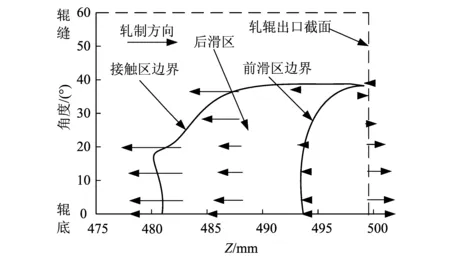
图4 节点速度与轧辊线速度差异Fig.4 Velocity differences between node points and roller
图4为管坯表面与轧辊接触点相对切向速度分布,各区域边界为大致分界。由图可知,速度矢量方向与轧制方向相同,表示该节点速度快于所处位置轧辊线速度,为前滑区,反之为后滑区。图中标示出了前滑区、接触区域大致的边界。矢量的长度说明了速度差异的大小,可以看出,在轧辊出口截面的辊顶处前滑趋势最大,并沿辊顶至辊缝,接触点轧辊线速度逐渐增加,前滑趋势减弱;在Z轴位置495mm附近,金属外表面与轧辊相对速度基本相等。图中还可以看出,金属在孔型入口处的后滑趋势最大,在出口处前滑趋势最大。
图5为2#机架孔型内部变形区外表面温度场分布。从图中可以看出,由于辊底两侧首先和钢管外表面接触,这两区域率先发生温度下降;并由于金属内部热量传导,金属通过孔型后外表面温度逐渐趋于相同。

图5 2#机架孔型内变形区表面温度场分布Fig.5 Surface temperature field distributions of the deformation area in 2# pass
4实验验证
图6-a为第三机架孔型出口断面图,图6-b为该仿真同工艺轧卡实验锯切后的截面。通过比对,两图形状基本相似。经过测量,管坯周向外径绝对误差最大值0.148mm,相对误差0.32%;周向壁厚绝对误差最大值为0.03mm,相对误差为0.49%。无网格法仿真的结果与实验实测值基本吻合,如图7所示。

图6 产品形状对比Fig.6 Product shape contrasts
5结论
本文采用无网格配点法构建了温度场刚度矩阵,使方程构建过程与两物理场耦合过程得以简化。由于实验检测条件限制,没有测得管坯轧制过程中的温度变化数据,但纵连轧工艺数值模拟与实验测量所得管坯尺寸数据对比表明,本文所建立的无网格模型是正确的、有效的。

图7 外径(a)、壁厚(b)仿真与实验测量对比Fig.7 Contrasts between numerical simulations and experimental measurements of diameter (a) and thickness (b)
参考文献:
[1]张雄,刘岩.无网格法[M].北京:清华大学出版社,2005.
[2]LIUGuirong.Meshfreemethods:movingbeyondthefiniteelementmethod[M].US:CRCPRESS,2003.
[3]CHENJS,ROQUECMOL,PANChunhui,etal.Analysisofmetalformingprocessbasedonmeshlessmethod[J].JournalMaterialsProcessingTechchnology,1998,80-81:642-646.
[4]YOONSP,WUCT,WANGHuiping,etal.Efficientmeshfreeformulationformetalformingsimulation[J].JounalofEngineeringMaterialsandTechnology,2001,123(4):462-467.
[5]赵国群,王卫东,栾贻国.金属塑性成形过程无网格伽辽金法数值模拟技术研究[J].机械工程学报,2004,40(11):13-16.
[6]LIGuangyao,SIDIBEK,LIUGuirong.Meshfreemethodfor3Dbulkforminganalysiswithlowerorderintegrationscheme[J].EngineeringAnalysiswithBoundaryElements,2004,28(10):1283-1292.
[7]孙杰,胡建华,双远华,等.斜轧延伸过程的无网格RPIM方法数值模拟[J].四川大学学报(工程科学版),2013,45(1):67-73.
[8]CHENJS,WANGHuiping.Newboundaryconditiontreatmentsinmeshfreecomputationofcontactproblems[J].ComputerMethodsinAppliedMechanicsandEngineering,2000,187(3):441-468.
[9]REBELON,KOBAYASHIS.Acoupledanalysisofviscoelasticdeformationandheattransfer[J].InternationalJournalofMechanicalScience,1980,22(11):707-718.
(编辑:庞富祥)
Meshless Thermo-mechanical Analysis of Continual Mandrel Rolling Process for Seamless Steel Tube
ZHOU Yana,c,SHUANG Yuanhuab,c,ZHAO Chunjiangb,c,GOU Yujunb,c,LIU Qiuzua
(TaiyuanUniversityofScienceandTechnology,a.CollegeofMechanicalEng.,b.CollegeofMaterialSci.andEng.,c.CollaborativeInnovationCenterofTaiyuanHeavyMachineryEquipment,Taiyuan030024,China)
Abstract:In this paper, the meshless moving least square approximated functions were corrected by using the mixed transformation method in order to enforce the essential boundary conditions. The stiffness matrices of the velocity field were the temperature field were constructed using the meshless Galerkin method and the meshless collocation method,respectively. The solutions of the two coupled fields were calculated with the indirect coupling method. Finally a formula was derived for the rigid-plastic meshless thermo-mechanically coupled analysis for the simulation of the continual mandrel rolling process. The comparison between the simulation and the experiments shows good accordance, validating the reliability and precision of our meshless method.
Key words:seamless steel tube;continual mandrel rolling process;meshless method;thermo-mechanical analysis
文章编号:1007-9432(2016)02-0160-05
*收稿日期:2015-08-20
基金项目:山西省科技攻关项目:镁合金管材可控张力热连轧工艺与设备开发(20140321008-08);国家自然科学基金资助项目:薄壁管材高速旋压工艺拟动力学特性及可控机理研究(51375325)
作者简介:周研(1983-),男,湖南宁乡人,博士生,主要从事无缝钢管轧制工艺及设备、轧制过程的数值模拟研究,(E-mail)zy_harry@vip.163.com
中图分类号:TG335.71
文献标识码:A
DOI:10.16355/j.cnki.issn1007-9432tyut.2016.02.007

