具有状态时滞的Markov切换系统的稳定条件

盛遵冰，陆　磊，吕东方，丛　屾，*

(1.黑龙江大学 机电工程学院，哈尔滨 150080;2.烟台冰轮重型机件有限公司，山东 烟台 264006)



具有状态时滞的Markov切换系统的稳定条件

盛遵冰1，陆磊2，吕东方1，丛屾1，*

(1.黑龙江大学 机电工程学院，哈尔滨 150080;2.烟台冰轮重型机件有限公司，山东 烟台 264006)

摘要：考虑时滞Markov切换系统的均方指数稳定性分析。在不计及Brown运动的条件下,由于Markov切换系统仍然遵循Riemann-Lebesgue意义下的微积分法则。因此基于较为一般的Lyapunov-Krasovskii泛函构造方式,系统地推广了时滞系统稳定性研究中的解析方法与技巧。通过引入自由参数矩阵,建立了以线性矩阵不等式所表述的与时滞相关的稳定性判据,由此给出了均方指数稳定性的完整证明。仿真算例证实了方法的有效性。

关键词：Markov切换系统;状态时滞;稳定性分析;线性矩阵不等式

0引言

Markov切换系统是由若干子系统在满足一定统计规律的逻辑变量的驱动下构成的随机动力系统,其逻辑变量的演化过程由Markov概率转移矩阵生成,并触发子系统的依次交替作用。

本文考虑具有状态时滞的Markov切换系统的均方指数稳定性问题。Markov切换系统的基本理论是在最近20 a发展起来的,其稳定性研究的思想与方法基本上源于文献[1-3]的工作。与此同时,时滞系统稳定性问题也成为研究热点,工作主要集中于一般形式的Lyapunov-Krasovskii泛函的构造与解析技巧方面,以减少由时滞大小及其变化率所引起的保守性;其中,普通微积分运算的一些基本原理,例如Leibnitz-Newton公式与分部积分公式,是至关重要的[4-6]。

在概率空间中存在多种意义下的收敛性定义,随机系统的稳定性相应地被赋予不同的含义[7-8],其中均方稳定与依概率稳定较为常用。虽然Markov切换系统归于随机系统范畴,但是其干扰项可以在确定意义下予以考虑[9-11]。因此,不同于在It微积分意义下所考虑的带有Brown运动的随机系统[12],Markov切换系统的右端满足所谓的Caratheodory条件[13],其连续状态的微积分仍然是在Riemann-Lebesgue意义下的普通运算。因此,根植于普通微积分法则的时滞系统稳定性分析方法与技巧可以适当地推广至Markov切换系统,从而为相应Lyapunov-Krasovskii泛函的构造及解析提供了方便。如果计及Brown运动,那么Brown运动与It随机微积分的基本性质,例如独立增量性及It同构定理[14-15],具有决定性作用[16]。

在相关的研究结果中,以特殊形式的Lyapunov-Krasovskii泛函构造方法居多,即泛函具有相同的积分项,因此其解析过程沿袭了普通微积分运算,未能体现Markov过程的统计规律[10,16-18]。本文目的是基于较为一般的泛函构造方式,系统地推广可以有效减少保守性的解析方法与技巧,从而建立与时滞相关的稳定性判据;同时给出证明时滞Markov切换系统均方指数稳定性的完整过程。

1系统描述

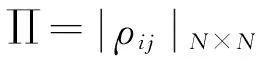
考虑具有状态时滞的Markov切换系统:

(1)

(2)

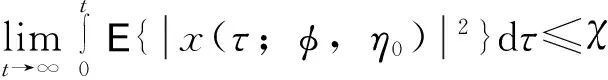
2主要结论

(3)

其中

(4)

(5)

(6)

定理1对于泛函(3),存在α,β>0,使得:

(7)

并且式(4)～式(6)在无穷小生成算子(2)作用下的表达式分别为：

(8)

(9)

(10)

从而得到:

式(8),式(9)的证明过程参见文献[3],以下论证式(10)。根据Markov性可知：

由此根据式(2),即可得证。证毕。

(11)

(12)

(13)

(14)

(15)

其中各项分别为:

因此通过式(14)得到：

(16)

进而,由式(12),式(16)推知：

(17)

(18)

假定λ>0为下列超越代数方程的唯一解:

(19)

其中α,β>0为不等式(7)右端的系数。设Vλ(x,ηt,t)=eλtV(xt,ηt,t),从而有:

(20)

因此根据Dynkin公式得到:

(21)

结合式(7),式(18),式(20),式(21)推知：

(22)

通过积分变量代换与交换积分次序可知:

将上式代入式(22)右端得到：

由此,依据等式(19)即得:

因此,若给定{x0=φ∈Cn,2h,η0},则EVλ(xt,ηt,t)是一致有界的。从而根据:

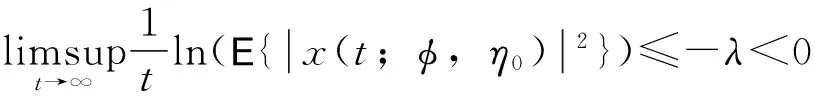
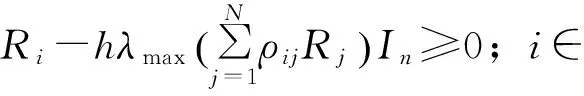
注释2不等式(18)与超越方程(19)及其均方指数稳定性结论在形式与Halanay不等式[19]是类似的。由此产生这样的问题:上述证明均方指数稳定性的过程是否可以提炼为随机意义下的Halanay型不等式以便应用。此问题具有一定难度,而其理论与应用价值是非平凡的。

3仿真分析

注释3仿真计算可知,作为确定性系统而言,此时两个子系统均不稳定。由此可见,随机意义下的稳定性与确定意义下的稳定性之间并无必然的因果联系。

4结论

对于时滞Markov切换系统的稳定性问题,为避免解析困难,多数文献选择具有相同积分项的Lyapunov-Krasovskii泛函,从而其构造有失一般性;而且在给出泛函经过无穷小生成算子作用的结果之后,回避了均方渐近稳定或均方指数稳定的证明过程。本文方法突出了Markov切换系统的随机特征,基于较为一般的泛函构造形式,考虑了在相同微积分法则作用下推广时滞系统稳定性分析方法的可能性,由此建立了时滞Markov切换系统的与时滞相关的稳定判据,其中一些附加约束条件说明了推广过程中的难点及特殊性。进而严格论证了均方指数稳定性,并仿真验证了结论的有效性。

参考文献：

[1]JiY,ChizeckHJ.Controllability,stabilizabilityandcontinuous-timeMarkovianjumplinearquadraticcontrol[J].IEEETrans.onAutomaticControl, 1990, 35(7): 777-788.

[2]FengX,LoparoKA,JiY,etal.Stochasticstabilitypropertiesofjumplinearsystems[J].IEEETrans.onAutomaticControl, 1992, 37(1): 38-52.

[3]QianW,LiT,CongS,etal.Stabilityanalysisforintervaltime-varyingdelaysystemsbasedontime-varyingboundintegralmethod[J].JournaloftheFranklinInstitute, 2014, 351: 4892-4903.

[4]CongS,ZouY.Anewdelay-dependentexponentialstabilitycriterionforItostochasticsystemswithMarkovianswitchingandtime-varyingdelay[J].Int.J.SystemsScience, 2010, 41(12): 253-270.

[5]CongS.Onexponentialstabilityconditionsoflinearneutralstochasticdifferentialsystemswithtime-varyingdelay[J].Int.J.Robust&NonlinearControl, 2013, 23(11): 1265-1276.

[6]GuKQ.AfurtherrefinementofdiscretizedLyapunovfunctionalmethodforthestabilityoftime-delaysystems[J].Int.J.Control, 2001, 74(10): 967-976.

[7]KushnerH.StochasticStabilityandControl[M].NewYork:Academic, 1967.

[8]Has’minskiiRZ.StochasticStabilityofDifferentialEquations[M].Rockville:Sijthoff&Noordhoff, 1981.

[9]CongS.Newstabilitycriterionoflinearsingularsystemswithtime-varyingdelay[J].Int.J.SystemsScience, 2014, 45(9): 1927-1935.

[10]WuJ,ChenT,WangL.Delay-dependentrobuststabilityandH-infinitycontrolforjumplinearsystemswithdelays[J].Systems&ControlLetters, 2006, 55(11): 939-948.

[11]WangS,LiY,WuY.Observer-basednon-fragilepassivecontrolforuncertainnonlinearsampled-datasystemwithtime-delay[J].Int.J.Computerscommunications&Control, 2014, 9(4): 482-496.

[12]MaoX,YuanC.StochasticDifferentialEquationswithMorkovianSwitching[M].London:ImperialCollegePress, 2006.

[13]HaleJ.TheoryofFunctionalDifferentialEquations[M].NewYork:Springer-Verlag, 1977.

[14] ØksendalB.StochasticDifferentialEquations[M]. 2ndedition,Berlin:Springer-Verlag, 1989.

[15]MohammedS-EA.StochasticFunctionalDifferentialEquation[M].NewYork:LongmanScientific&Technical, 1986.

[16]YueD,HanQL.Delay-dependentexponentialstabilityofstochasticsystemswithtime-varyingdelay,nonlinearity,andMarkovianswitching[J].IEEETrans.onAutomaticControl, 2005, 50(2): 217-222.

[17]CaoYY,LamJ,HuLS.Delay-dependentstochasticstabilityandH-infinityanalysisfortime-delaysystemswithMarkovianjumpingparameters[J].J.FranklinInstitute, 2003, 43(6): 423-434.

[18] 董春卫，印凡成.具有Markov切换的随机Logistic系统持久性和灭绝性研究[J].黑龙江大学自然科学学报，2015，32(5)：571-579.

[19]KolmanovskiiVB,NosovVR.StabilityofFunctionalDifferentialEquations[M].NewYork:Academic, 1986.

Stability conditions for Markovian switching systems with state-delay

SHENG Zun-Bing1，LU Lei2，LV Dong-Fang1，CONG Shen1，*

(1.SchoolofMechanicalandElectricalEngineering,HeilongjiangUniversity,Harbin, 150080,China;2.YantaiMoonFoundryCo.,Ltd,Yantai264006,Shandong,China)

Abstract：This note is concerned with the stability analysis in the mean square sense for Markovian switching systems with state-delay. The calculus rules in Riemann-Lebesgue sense are available for Markovian switching systems when the Brownian motion is not accounted. Then, based on the complete form of Lyapunov-Krasovskii functional, the existent methods and techniques for deterministic time-delay systems are generalized systematically. By introducing relaxation matrices, the delay-dependent stability criterion is estabilished in terms of linear matrix inequality, through which the exponential stability in the mean square is strictly verified. Numerical example demonstrates the proposed approach.

Key words：Markovian switching systems; state-delay; stability analysis; linear matrix inequality

DOI:10.13524/j.2095-008x.2016.01.015

收稿日期：2015-11-19

基金项目：国家自然科学基金资助项目(61573131)；黑龙江省自然科学基金资助项目(LC201428)

作者简介：盛遵冰(1977-)，男，山东济源人，讲师，博士，研究方向：视觉伺服与运动控制,E-mail:zunbingsheng@163.com；*通讯作者：丛屾(1976-)，男，黑龙江哈尔滨人，副教授，博士，研究方向：切换系统与随机系统，E-mail:2009040@hlju.edu.cn。

中图分类号：TP13

文献标志码：A

文章编号：2095-008X(2016)01-0079-08

网络出版地址：http://www.cnki.net/kcms/detail/23.1566.T.20160309.0910.008.html