闸后扩散式消力池池深的简化计算法

滕　凯

(齐齐哈尔市水务局，黑龙江 齐齐哈尔 161006)



闸后扩散式消力池池深的简化计算法

滕凯

(齐齐哈尔市水务局，黑龙江 齐齐哈尔 161006)

摘要：闸后扩散式消力池池深计算需联立求解高次方程，常规的数学方法不能直接获得。现有的图解法及试算法或是求解过程依赖图表精度差，或是计算过程繁琐工作效率低，而利用微机编程获解又不便基层工程技术人员应用。经对池深水力计算相关公式的整理变换，采用优化拟合的方法，完成了对无量纲求解方程的拟合替代，在工程实用参数范围内，获得了可直接完成扩散式消力池池深求解的简化计算公式，计算过程简捷直观、成果精度满足工程设计要求。为此，文章以实例加以论证。

关键词：扩散式消力池；池深；优化拟合；简捷计算；实例

池式消能工是闸后消能设计选取的主要结构形式，因此《水闸设计规范》通过附录的形式专门给出了池式消能工关于池深的计算公式。由于该种消能工的水力计算涉及求解繁复的超越方程[1-3]，无法通过常规的数学方法完成求解，为了简化求解过程，相关学者开展了大量的研究工作，并获得了许多有益的研究成果。文献[4-10]分别给出了当b1/b2=1(b1、b2分别为消力池首及末端的宽度)情况下借助图表试算、直接试算、简化计算及智能求解的池深计算方法。但在实际水闸工程中，由于闸室的总布置宽度常常小于闸后渠(或河)道的底宽，为了获得更好的消能效果及与下游渠(或河)道的水流衔接，工程上多将闸后消力池设计为扩散式，而有关扩散式消力池池深计算方法的研究则相对较少[11]，为此，文献[11]通过建立动量方程给出了扩散式消力池池深的试算获解方法，计算过程较繁复，不便应用。

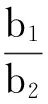
1基本计算公式

底流消能的挖深式消力池如图1所示，当在池中发生完整的淹没式水跃，并与下游渠道(或河道)水面形成自然衔接时，池深d的确定需联立求解下列方程：

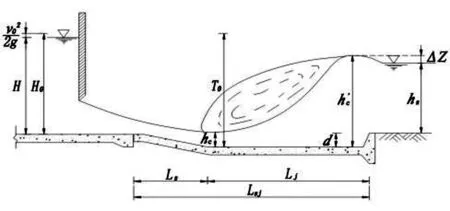
图1　水闸消力池消能简图

(1)

(2)

(3)

(4)

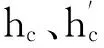
将式(4)代入式(1)减式(3)经整理可得：

(5)

(6)

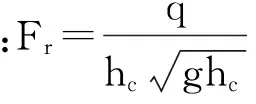
式中：x为中间变量；Fr为弗汝德数。

由式(6)可得：

(7)

(8)

式中：η为已知参数。

将式(7)、(8)代入式(5)整理得：

(9)

在式(9)中，设：

(10)

根据水力学原理可得：

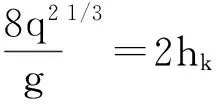
(11)

则式(10)为：

(12)

式中：hk为临界水深，m；t0为下游渠道(或河道)护底以上的总水头，m；E为已知综合参数。

将式(12)代入式(9)可得：

(13)

在式(13)中，因当过闸流量Q为已知时，H0、q即可根据闸前渠道(或河道)的断面参数及闸室宽度求得，进而t0、hk及E可求，则式(10)即为含有1个未知数x的超越方程，可通过采用试算或迭代(整理出迭代形式)法可完成求解。

2简化公式的建立及精度分析

2.1公式的建立

因式(13)为较繁杂的超越方程，无论采用试算法还是迭代法均需借助计算机编程完成，不便实际应用，为此，本文提出以下简化计算法。

y=x2-1

(14)

将式(14)代入式(13)得：

(15)

式中：y为引入的中间变量。

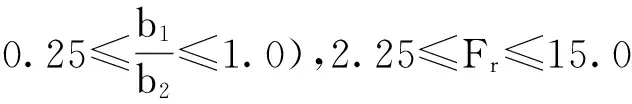
(a)η=1

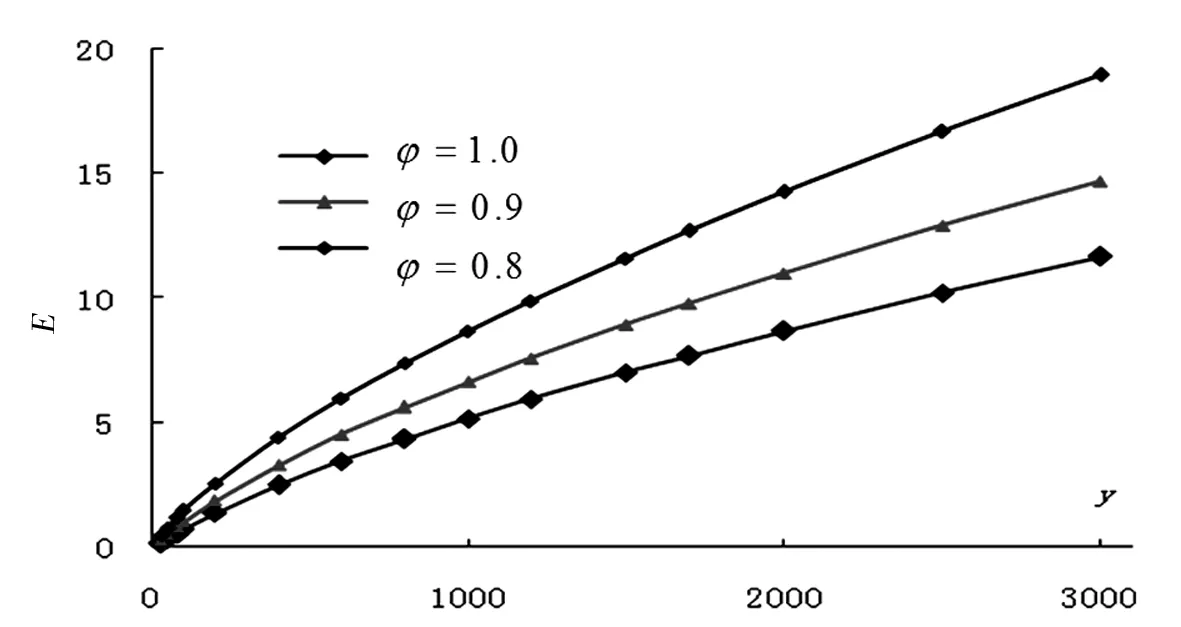
(b)η=0.7

由图2可见，当φ、η为定值情况下，E随y的增大呈非线性增加，构成的Ei～yi曲线类型具有较好的抛物线关系。为此，提出以下拟合替代备选函数：

Ay2α+Byα+C=E

(16)

Ay2α+Byα+C=InE

(17)

Ay2α+Byα+C=eE

(18)

采用优化拟合的方法，以标准剩余差最小为目标函数，即为：

(19)

式中：n为数值拟合分析计算的数组数。

经逐次逼近拟合比选[15-16〗可知，式(16)拟合效果最好，并可获得式(15)的最优替代式为：

Ay2/3.37+By1/3.37+C=E

(20)

其中：A=0.131413φ-2-0.025598η-0.67+0.039922；B=1.615939η-0.23-0.259066φ-2-1.956872；C=0.335885φ-2-0.136459η-2.55+0385221。

式中：A、B及C均为中间参数。

由式(19)即可求得y为：

(21)

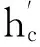
2.2精度分析

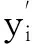
AI2.0将推动人工智能迈向新的阶段，即从人工知识表达技术到大数据驱动知识学习技术，人工智能的实现方法正转变为从大数据中进行知识发现和学习，使得机器学习从表象深入到综合推理；从聚焦研究“个体智能”到基于互联网络的群体智能，形成群智能力的互联网服务创新（如共享经济）体系；从只能处理类型单一的数据到能够综合视觉、听觉、文字等多种媒体的语义，人工智能正在迈向跨媒体认知、学习和推理的新高度；从追求“智能机器”和高水平的人机与脑机交互技术，走向人机混合的增强智能；从机器人到自主智能系统。

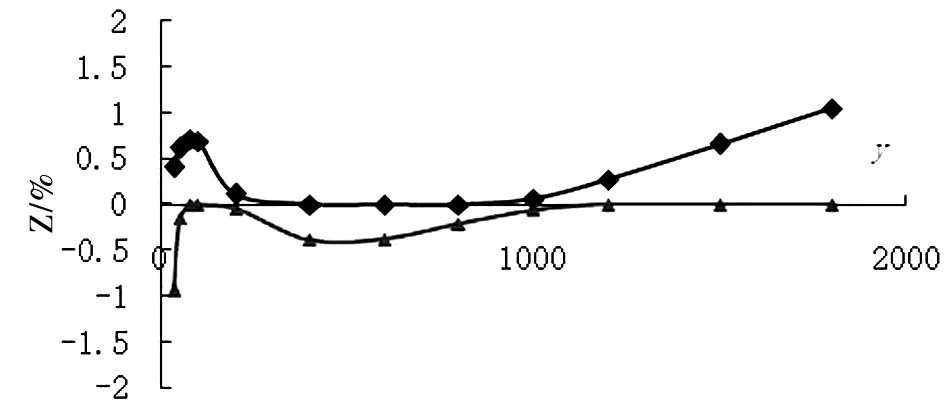
图3　计算y值的误差包络线

(22)

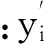
(23)

(24)

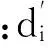
(25)

当z=-0.94%时

(26)

3计算实例

已知某堰高为P=3m(相对于下游渠底)的溢流坝，堰顶部设有闸门控制，过水单宽流量为q=m3/(s·m)，φ=0.90。下游为底宽16m、边坡比为1∶2.5的梯形断面渠道，相应于过闸流量的水深为hs=2.75m。闸后设b1=12m、b2=16m的矩形消力池，试计算当闸前水头4.0m时的消力池深d。

由上述已知条件可求得：H0=7.0374m，hk=1.5425m，t0=2.8168m，E=1.3682m。根据式(20)～(22)可分别求得：A=0.1752985，B=-0.6338129，C=0.6359646，则由式(23)可得：

(27)

(28)

根据式(1)～(4)利用计算机编程，通过逐次逼近即可求得池深的精确解为d=0.634m，本文方法求解结果的相对误差为0.32%。由此可见，本文方法具有较好的求解精度。

4结语

消力池深计算是水闸工程底流消能设计的重要环节，因此，开展有关简化计算方法的研究对提高设计工作效率及精度具有重要意义。本文通过对整理后的无量纲求解方程的拟合替代，获得了可直接完成相关参数求解的简化计算公式，仅借助计算器即可非常简捷地完成池深求解，计算过程大大简化。误差分析及实例计算表明，在工程适用参数范围内，求解精度完全满足工程计算要求，具有较好的实用推广价值。

参考文献：

[1]华东水利学院主编.水工设计手册[M]. 北京：水利电力出版社，1983.

[2]武汉水利水电学院水力学教研室主编.水力计算手册[M]. 北京：水利电力出版社，1983.

[3]SL265—2001水闸设计规范[S].北京：中国水利水电出版社，2001.

[4]程应昌.介绍一种消力池水力计算的图解法[J].水利科技，1980，(2)：11-15.

[5]辛孝明.设计综合式消力池的简便计算[J].山西水利科技，2007，(1)：56-57，,6.

[6]张志军，陶卫.计算消力池深度的一种新方法[J].中国农村水利水电，2000，(5)：16-17.

[7]滕凯.消力池深的简化计算法[J].人民长江,2012,43(15)：77-79.

[8]张志昌，李若冰.基于动量方程的挖深式消力池深度计算[J].西北农林科技大学学报(自然科学版)，2012，40(12)：214-218.

[9]刘仲桂，陈振坤，王乐秀. 消力池的水力计算[J].广西科学院学报，1986，(1)38-44.

[10]叶培聪，许小健.遗传算法工具箱在消力池水力计算中的应用[J].科学技术与工程，2008，(7)：262-263,267.

[11]张志昌，傅铭焕，赵莹，等.平底渐扩式消力池深度的计算[J].武汉大学学报(工学版)，2013，46(3)：295-299.

[12]谢成玉,滕凯.三次抛物线形渠道断面收缩水深的简化计算[J].南水北调与水利科技,2012,10(2)：148-150.

[13]谢成玉,滕凯.抛物线形断面渠道均匀流水深的近似计算公式[J].水电能源科学,2012,30(7):94～95,172.

[14]滕凯.半立方抛物线形渠道正常水深的近似计算公式[J].长江科学院院报，2012,29(12)：30-32.

[15]王慧文.偏最小二乘回归法及其应用[M].北京国防工业出版社，1999.

[16]阎凤文.测量数据处理方法[M].原子能出版社，1988.

Simplified Calculation Method of Diffusive Stilling Pool Depth behind Gate

TENG Kai

(Qiqihaer Urban Water Affairs Bureau，Qiqihaer 161006，China)

Abstract：To calculate the depth of diffusive stilling pool behind the gate needs to be simultaneous with high order equations，can't be gotten by the conventional mathematical method directly. The existing graphic method and trial method is low in accuracy due to depending on the figures and charts during the solution process，or low in working efficiency because complex calculation process，but solutions obtained by computer process are not convenient for technique personnel working in-sit to apply. Through regulation and transmission for the formulas relevant with pool depth hydraulic calculation，the optional fit method was adopted to replace the fit of dimensionless equation，within the scope of practical project parameters，the simplified calculation formulas to calculate directly the depth of diffusive stilling pool were gotten，the calculation process is simple and intuitive，the result accuracy may meet the engineering design demands. Therefore，the paper demonstrates in example herein.

Key words：diffusive stilling pool；depth of pool；optional fit；simple calculation；example

文章编号：1007-7596(2016)04-0046-05

[收稿日期]2016-03-23

[作者简介]滕凯(1957-)，男，齐齐哈尔人，高级工程师，现任单位总工程师，从事水利防灾减灾及工程优化设计研究。先后获齐齐哈尔市政府市长特别奖一项，齐齐哈尔市政府科技进步一等及三等奖各一项。先后被中共黑龙江省委评为“创业、创新、创优”优秀共产党员，被省水利厅先后授予“全省水利科技工作先进个人”、“全省水利工程建设先进个人”。截至目前，已在《水利学报》、《水利水电科技进展》、《长江科学院院报》、《水文》、《人民长江》、《人民黄河》、《南水北调与水利科技》、《水电能源科学》、《华北水利水电大学学报》等省部级以上刊物发表论文140余篇。

中图分类号：TV131.4

文献标识码：A