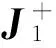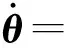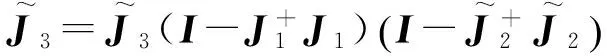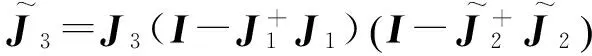基于任务分解和速度分配的机器人运动规划*
张勤 范长湘
(华南理工大学 机械与汽车工程学院, 广东 广州 510640)
基于任务分解和速度分配的机器人运动规划*
张勤范长湘
(华南理工大学 机械与汽车工程学院, 广东 广州 510640)
摘要:为了克服机器人在奇异点附近的运动障碍,提出基于任务分解和速度分配的机器人运动规划方法:将控制任务按照优先顺序分解成若干项子任务分别进行控制;根据电机的驱动能力和任务优先顺序确定各项子任务的速度分配,以便在机器人处于奇异姿态或在奇异姿态附近,其灵活性降低的情况下,机器人也能够协调运动,保证重要控制目标的实现,避免由于速度突变造成的机器人抖动、末端误差过大和控制系统不稳定现象.最后以PUMA机器人为例,说明了控制系统的构成,并通过仿真证明了文中方法的可行性.
关键词:机器人;运动规划;任务分解;速度分配;奇异姿态
机器人的运动规划是实现高速、高精度、高稳定性操作的重要保证.当机器人处于奇异位形时,速度雅可比矩阵降秩,末端执行器自由度减少,机器人的灵活性降低,在这种情况下,如何克服机器人在奇异点附近的运动障碍,保证重要控制目标,已经成为了当前国内外机器人领域的研究热点.
奇异点的存在是机器人的一个固有特性,包括结构边界奇异问题和内部奇异问题.针对机器人的结构边界奇异问题,目前比较常用的方法是把关节极限角度作为边界约束,通过优化对关节角的输出进行控制,防止关节角超限.而对于内部奇异问题,Wampler等[1]提出“阻尼最小方差”修正雅可比矩阵的方法,通过选择合适的阻尼因子,保证奇异区域内关节速度的连续性,实现奇异区域的平稳过渡,但该方法无法避免由此产生的机器人末端的控制误差;Chiaverini[2]对上述方法进行了改进,提出“阻尼最小方差+数值滤波”的方法,综合考虑轨迹规划精度和关节速度的关系,提高了机器人末端位置精度.Cheah等[3]通过奇异区域内运动参数调整,奇异区域外偏差补偿的方法,实现了机器人跨越奇异区域或者从奇异区域启动.文献[4-5]采用奇异分离和阻尼优化的方法,分离出机器人运动中影响奇异的参数,实现机器人的关节速度在奇异区内连续平滑的同时,还可以保证机械人末端在某些方向的控制精度.综合以上分析可以看出,上述研究主要是考虑如何回避奇异点,保证奇异区域内各关节速度的平稳性,但一般是以牺牲机器人末端的控制精度为代价.
增加机器人的关节自由度数,能够有效提高机器人的灵活性.通过冗余机器人的自运动能力,机器人能在完成作业目标的同时,尽力实现回避奇异位形、躲避障碍、容错控制以及改善动力学性能等操作[6-7].在冗余机器人的控制中,逆运动学的求解是关键.目前普遍使用的求解方法主要有扩展雅可比矩阵法、基于四元数求解法和梯度投影法等.Baillieul[8]提出扩展雅可比矩阵方法,将机器人回避奇异位形和躲避障碍等任务作为约束加入机器人的求解运算中,把雅可比矩阵扩展为方阵进行求解.基于四元数求解法是基于旋量理论描述机械人的空间方位,可以在一定范围内回避奇异姿态,但容易引起系统的不稳定[9-10].Liegeois[11]提出的梯度投影算法是应用最为广泛的方法,其将冗余机器人关节速度的通解表示为特解与对应的齐次项之和,通过评价函数或者子任务来确定齐次解,优化控制.以此为基础,根据不同的控制目标,确定齐次解,提出了诸多的优化方法.Yoshikawa、姚建初等[12-13]以机器人的可操作性作为评价,在奇异姿态的回避上得到很好的应用.针对现有算法中普遍存在的奇异姿态附近关节速度过大的问题,Colome等[14]基于雅可比矩阵奇异值修正滤波和设定可变阻尼的方法,对逆运动学的求解进行了改进,使机器人奇异姿态附近的运动更加平稳,但计算量大,限制了其应用范围.文献[7,15]提出基于任务优先级的冗余控制方法,根据冗余机器人的能力优先保证优先级别高的任务,再依次尽力完成级别低的任务,但也无法避免奇异区域内关节速度过大的现象.针对这个问题,文献[16]提出了冗余机器人的反馈运动控制方法.在以上研究的基础上,本研究将基于任务分解的冗余控制思路应用于非冗余机器人控制中,并进行了改进,提出基于任务分解和速度分配的机器人运动规划方法,也就是TDSD(Task-Decomposition and Speed-Distribution)法.按照目标任务的优先级别将控制任务分解为各项子任务,分别进行控制;根据电机的驱动能力和任务优先级,确定各项子任务的速度分配,这样在机器人处于奇异姿态或在奇异姿态附近时,即使灵活性降低,机器人也能够协调运动,保证重要控制目标的同时缓慢通过其奇异位形.最后以PUMA机器人为例说明了控制系统的构成,并通过仿真证明了所提出的方法的可行性.
1基于TDSD的控制系统构成
1.1方法的提出及其数学描述
多自由度的机器人通常完成复杂的操作,在机器人控制任务的实现过程中,作业目标不同,机器人优先保证的任务也不同.比如:在焊接操作中,通常机械手末端的位置比姿态更为重要;在一些旋转装配作业中,相对于机械手的末端轨迹,其姿态更为重要;在液体搬运操作中,经常需要保证盛具的位置和液面方向,而对盛具自身转动方向的自由度要求不高.针对不同的控制目标,将控制任务按照优先顺序分解成若干个子任务,分别进行控制,这样当机器人处于奇异姿态或者在奇异姿态附近,自由度减少时,机器人将首先保证优先级最高的任务,然后再根据机器人的能力,依次完成优先级别低的任务,满足控制的要求.
假设机器人具有n个自由度,其第i个关节角度表示为θi(i=1,2,…,n),对应的关节角度矩阵为θ,则对应的机械手末端位置和姿态为关节角度的函数y =f(θ),且

(1)
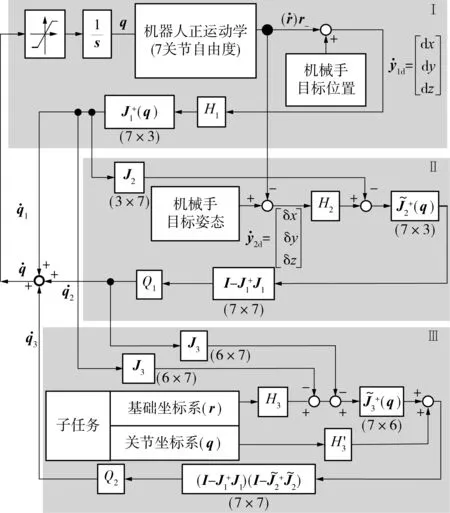
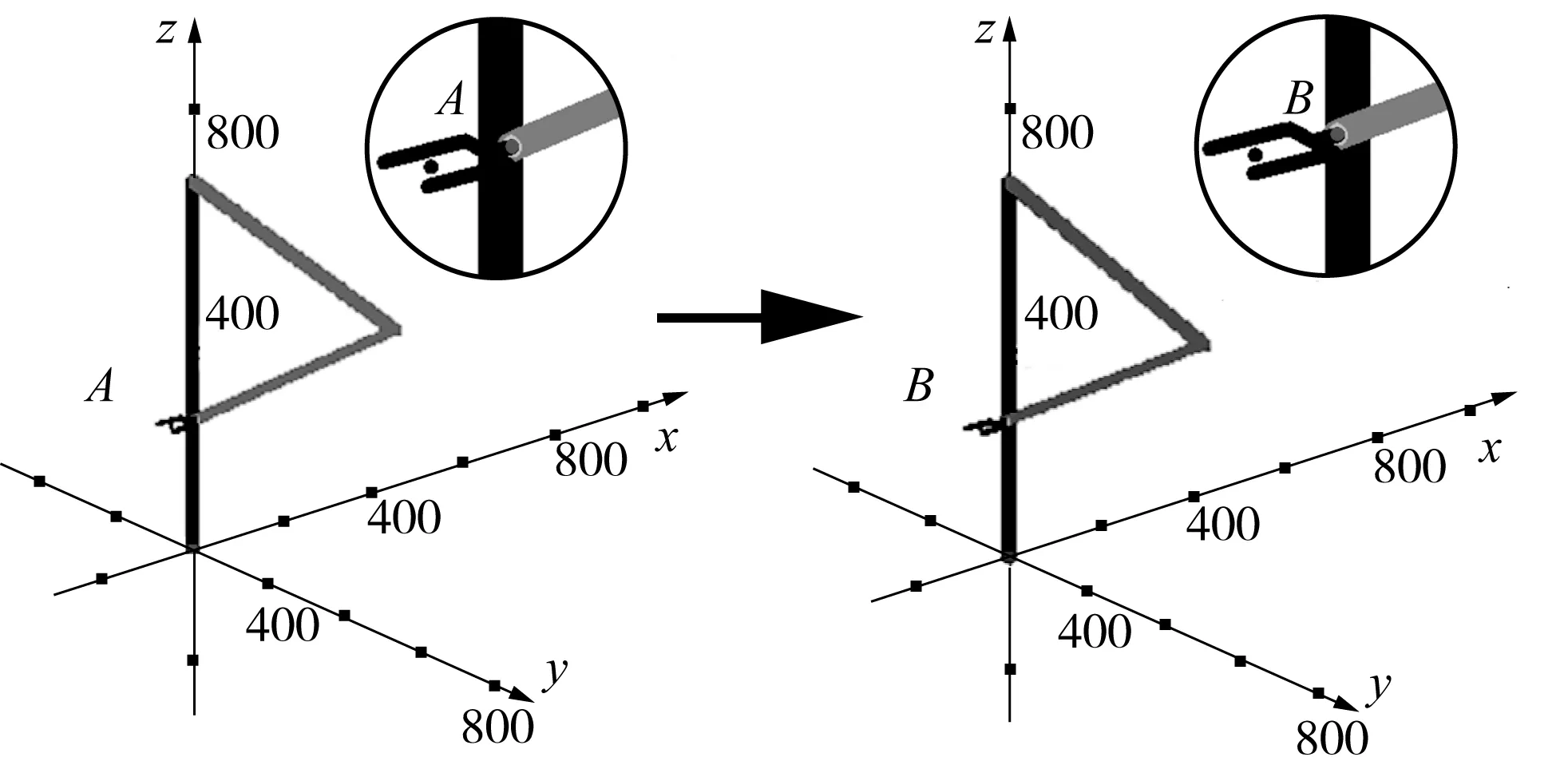
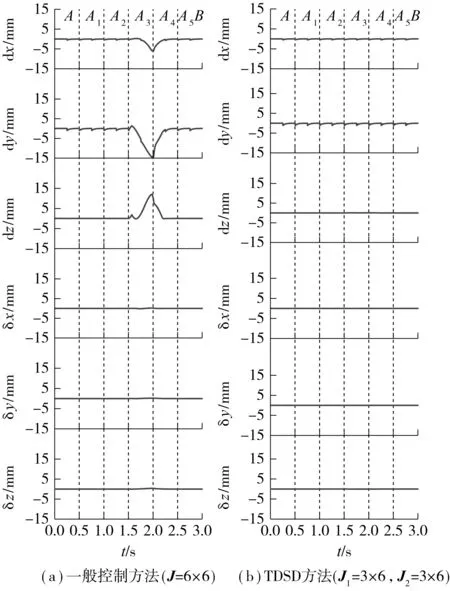
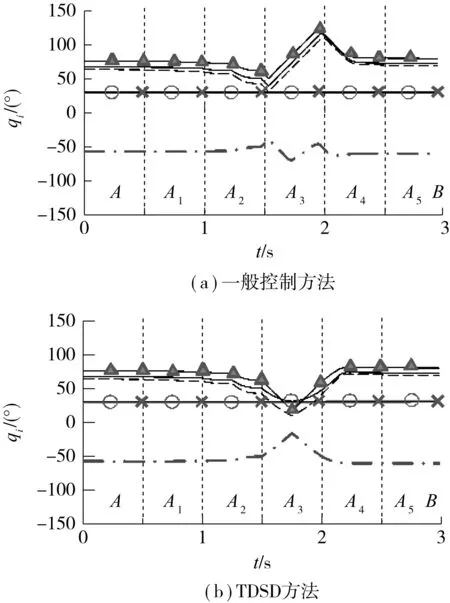
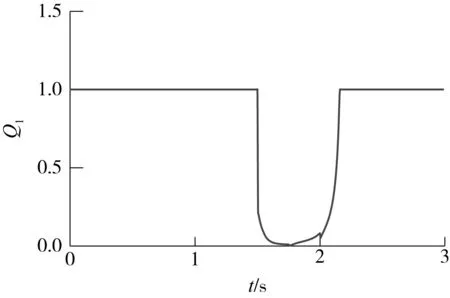
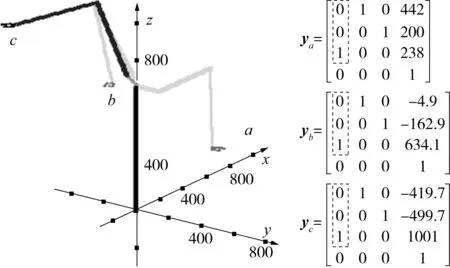
其中J为雅可比矩阵.根据优先顺序将目标任务分成若干目标子任务,子任务可以是给定的目标轨迹y1d,y2d,…,yid(i (2) (3) 由式(3)解得 (4) (5) (6) 当第2项子任务以评价函数p=V(θ)的形式给出时,通过保证p最大,确定通解中的k1值.可以设定k1= ξkp,其中ξ = [ξ1ξ2…ξn]T,而ξi= ∂V(θ) /∂θi,代入式(2)可得 (7) 综合以上的分析,可以看出目标关节速度可以看成是实现各项子任务的关联速度之和: (8) 1.2控制系统的构成 按照控制任务优先级将机器人的作业目标分解为各项子任务,对其进行分别控制,完成控制目标的机器人的关节速度可以分解为完成各项子任务需要的各关节速度的综合.以7自由度机器人为研究对象,以典型的空间6自由度作业任务为例,说明运动控制系统的构成. 考虑作业任务的一般性,假设将控制任务按照优先顺序分解为位置控制、姿态控制和优化控制3层子任务,各项任务分别控制,控制框图如图1所示. 图1 基于TDSD的机器人运动控制框图Fig.1 Block diagram of the kinematic control based on TDSD (9) (10) 根据以上设定,实际机器人目标关节速度为 (11) 通过速度分配系数Q1、Q2,驱动电机会优先保证优先级别高的位置控制需要的速度要求,然后是姿态,最后是优化条件.控制过程中,无需判定奇异位形的位置,控制系统根据式(9)或式(10),自动确定每个时刻Q1、Q2值,协调或者缓冲速度突变,保证重要的控制目标,避免通常的控制方法中机器人在奇异位形及奇异位形附近出现的目标轨迹误差过大或者陷入奇异位形不能逃脱的现象.假设p表示机械手末端的实际位置矢量,a、o、n分别为机械手末端姿态矢量;同样机械手末端的目标位置和姿态矢量分别为pd、ad、od、nd,则机械手末端的实际位置姿态和目标位置姿态的齐次变换矩阵分别为: ep=[dx,dy,dz]T=pd-p (12) 姿态误差通过式(13)求出[17]. (13) 2仿真实例 根据第1节的分析可知,按照任务的优先级别将控制任务分解为各项子任务,分别进行控制,根据电机的驱动能力和任务优先级,确定各项子任务的速度分配系数Q1、Q2,这样当机器人处于奇异姿态或在奇异姿态附近时,即使灵活性降低,机器人也能够协调或者缓冲速度突变,缓慢通过其奇异位形,保证重要控制目标. 以PUMA机械臂为例,通过仿真证明文中提出的控制方法的可行性. 2.1奇异姿态附近的运动规划 图2 PUMA型机器人模型Fig.2 Model of PUMA robot 图3 肩部奇异点附近机械臂的运动示意图(单位:mm)Fig.3 Schematic diagram of motion of the manipulator near the shoulder singularity(Unit:mm) PUMA型机械臂的结构如图2所示.图中l分别表示机械手各个连杆的长度.通常情况下,机械臂存在3种类型的奇异姿态:肩部、腕部和肘部奇异姿态.其中肩部和手腕部的奇异姿态在机械臂可动空间内的任何地方都可能存在.假设控制任务中需要保证机械手末端的位置和姿态,且位置控制更为重要.当机械臂末端从A点运动到B点时,如图3所示,机械臂将通过肩部奇异姿态及其附近,此时机械臂的灵活性大大降低.图中:la=671 mm,lb=ld=le=0,lc=433 mm,lf=433 mm,lg=50 mm.图4、图5示出了基于位置和姿态的一般控制方法和基于TDSA方法求得的机械臂末端从A点到B点运动过程中,其末端轨迹的位姿误差[dx,dy,dz,δx,δy,δz]T和各关节角度q的变化.从图4(a)、图5(a)可以看出,机械臂在奇异点附近区域(A2—A5区间)各关节速度突变,机械手末端出现了较大误差.为了避免这种情况发生,将控制任务分解为位置控制和姿态控制,并进行分别控制,根据各关节驱动速度容许值和式(9)确定Q1,可以缓冲速度突变,协调速度分配,使机械臂可以缓慢通过奇异姿态.对比图4、图5中的(a)和(b)可以看出,机械手在通过其肩部奇异姿态附近时,即使各关节角度突变,由于任务分解,对位置和姿态分别进行控制,以及Q1的调节作用,机械臂末端的目标位置仍然可以完全保证,机械手末端的姿态误差也大大减小.图6为从A点到B点运动过程中Q1的变化.在肩部奇异姿态附近(A2—A5),Q1<1,此区间内,机械臂优先满足控制机械手末端位置需要的速度,在此前提下,再尽量保证控制姿态需要的速度,在t=1.76 s附近,Q1近似为0,表示此时只能保证其末端的位置,而没有能力控制机械臂的姿态,此点对应的姿态误差应该为最大.在奇异区域以外的正常工作区域,Q1=1,与通常的位姿控制方法相同. 图4 肩部奇异点附近机械臂末端的位置和姿态误差Fig.4 Positional and orientational errors of the end-effecter near the shoulder singularity 图5 肩部奇异点附近的机械臂各关节角度变化Fig.5 Joint-angle changes of the manipulator near the shoulder singularity 图6 速度分配过程中Q1值的变化Fig.6 Changes of Q1 during speed-distribution 图7 PUMA机器人搬运液体示意图Fig.7 Schematic diagram of PUMA robot’s motion of transporting liquid 2.2液体搬运任务的运动规划 液体搬运过程中,笔者更关心的是搬运轨迹和保证盛具内的液体不洒落,而不在意盛具沿其轴线方向的转动.假设利用PUMA机械臂将水桶从a点经过b点搬到c处(如图7所示),且机械手各关节可动范围分别为q1∈[-160°,160°],q2∈[-225°,45°],q3∈[-45°,225°],q4∈[-110°,170°],q5∈[-100°,100°],q6∈[-266°,266°].在通常的控制方法中,虽然可以求得完成上述控制任务需要的各关节转角,如图8(a)所示,但从图中可以看出机械手腕部的角度超过了其关节的可动范围,实际控制也是无法完成的.为此可以将控制任务分解为控制水桶的位置和其法向的姿态[001]T(图7中的虚线框部分),剩余的自由度尽量保证机械手腕部转角q4、q5、q6在其可动角度范围中间附近.设定评价函数为 (14) 根据1.1节可以求得完成控制任务过程中,各关节角度的变化,如图8(b)所示.a、b、c点处的位姿分别为: 图8 机械臂各关节角度变化Fig.8 Joint-angle changes of the manipulator——关节角度变化;对应关节角度的可动范围;从这点开始关节角度超出其可动范围 对比图8(a)、8(b)可见,各关节的转角完全控制在其可动范围内,且满足控制目标要求. 3结论 文中提出基于任务分解和速度分配的防御性机器人运动规划方法.针对不同的控制目标,将控制任务按照优先顺序分解成若干项子任务,分别进行控制;根据电机的驱动能力和任务的优先级,确定各项子任务的速度分配,这样当机器人处于奇异姿态或在奇异姿态附近时,即使灵活性降低,也能够保证重要控制目标;通过改变奇异姿态附近的机器人各关节运动速度,可以避免由于速度突变造成的机器人抖动和末端误差过大以及控制系统不稳定的现象发生.与现有的控制方法相比,文中方法不需要复杂的运算,可以最大限度地利用机器人的驱动能力(自由度数),协调机器人运动平稳性与机械手末端精度的关系,能满足实际工程中需要.最后以PUMA机器人为例,说明了文中方法的可行性.文中方法适用于任何类型机器人的冗余和非冗余控制. 参考文献: [1]WAMPLER C W.Manipulator inverse kinematic solutions based on vector formulations and damped least-squares methods [J]. IEEE Transactions on Systems,Man and Cybernetics,1986,16(1):93-101. [2]CHIAVERINI Stefano.Singularity-robust task-priority redundancy resolution for real-time kinematic control of robot manipulators [J]. IEEE Transactions on Robotics and Automation,1997,13(3):398-410. [3]CHEAH C C,Li X.Singularity-robust task-space tracking control of robot [C]∥Proceediings of 2011 IEEE,International Conference on Robotics and Automation.Shanghai:IEEE,2011:5819-5824. [4]徐文福,梁斌,刘宇,等.一种新的 PUMA 类型机器人奇异回避算法 [J]. 自动化学报,2008,34(6):670-675. XU Wen-fu,LIANG Bin,LIU Yu,et al.A novel approach to avoid singularities of PUMA-type Manipulators [J]. Acta Automatica Sinica,2008,34(6):670-675. [5]刘海涛.工业机器人的高速高精度控制方法研究 [D]. 广州:华南理工大学,2012. [6]HANAFUSA H,YOSHIKAWA T,NAKAMURA Y.Analy-sis and control of articulated robot with redundancy [C]∥Proceedings of IFAC Symposium on Robot Control,8th Triennal World Congress.[S.l.]:IFAC,1981:1927-1932. [7]HANAFUSA H,YOSHIKAWA T,NAKAMURA Y.Redundancy analysis of articulated robot arms and its utilization for tasks with priority [J]. Transactions of the Society of Instrument and Control Engineers,1983,19(5):421- 426. [8]BAILLIEUL J.Kinematic programming alternatives for redundant manipulators [C]∥Proceedings of the IEEE International Conference on Robotics and Automation.St Louis:IEEE,1985:722-728 [9]De OLIVEIRA A S,De PIERI E R,MORENO U F,et al.A new approach to singularity-free inverse kinematics using dual-quaternionic error chains in the Davies method [J]. Robotica,2014:1-15.DOI:10.1017/S026357471 4001982.[10]SARIYILSIZ E,TEMELTAS H.A new formulation me-thod for solving kinematic problems of multiarm robot systems using quaternion algebra in the screw theory framework [J]. Turkish Journal of Electrical Engineering and Computer Science,2012,20(4):607-628. [11]LIEGEOIS A.Automatic supervisory control of the configuration and behavior of multibody mechanisms [J]. IEEE Transactions on Systems,Man,and Cybernetics,1977,7(12):868-871. [12]YOSHIKAWA T.Analysis and control of robot manipulators with redundancy [C]∥Proceedings of Robotics Research:The First International Symposium.Cambridge,MA:MIT Press,1984:735-748. [13]姚建初,丁希仑,战强,等.冗余度机器人基于任务的方向可操作度研究 [J]. 机器人,2000,22(6):501-505. YAO Jian-chu,DING Xi-lun,ZHAN Qiang,et al.On task-based directional manipulability measure of redundant Robot [J]. Robot,2000,22(6):501-505. [14]COLOME A,TORRAS C.Closed-Loop inverse kinema-tics for redundant robots:comparative assessment and two enhancements [J]. IEEE/ASME Transactions on Mechatronics,2015,20(2):944-955. [15]NAKAMURA Y,HANAFUSA H,YOSHIKAWA T.Task-priority based redundancy control of robot manipulators [J]. The International Journal of Robotics Research,1987,6(2):3-15. [16]張勤,神谷好承,関弘明.冗長制御系の概念を応用したマニピュレータの運動制御 [C]∥ロボット学会論文集,東京,日本,2001.ZHANG Qin,YOSHITSUGU K,HIROAKI S.Motion control of manipulator from concept of redundancy [C]∥Proceedings of the Robotics Society of Japan.Tokyo:Japan[s.n.],2001. [17]小林尚登,他.ロボット制御の実際 [C]∥計測自動制御学会.東京:1997. KOBAYASHI H,et al.Practical control of robot manipulators [C]∥Proceedings of The Society of Instrument and Control Engineers.Tokyo:[s.n.],1997. Motion Planning of Robot on the Basis of Task Decomposition and Speed Distribution ZHANGQinFANChang-xiang (School of Mechanical and Automotive Engineering, South China University of Technology, Guangzhou 510640, Guangdong, China) Abstract:In order to overcome the motion difficulties of robot near its singularities, a new motion planning algorithm is proposed on the basis of task decomposition and speed distribution.In this algorithm, the control task is divided into several sub-tasks according to their priorities, and each sub-task is controlled independently.The velocity component of each sub-task is determined according to the driving capability of joint motors and the priority of each sub-task, which helps implement the coordinated movement of robot even in the condition of low flexibility when the robot moves near the singularities or stays in the singularities, thus achieving the control objective and avoiding the vibration, excessive end-effector error and system instability caused by the sudden change of joint relative velocity.By taking a PUMA robot for example, the composition of the control system is illustrated, and the feasibility of the proposed method is proved via simulation. Key words:robot; motion planning; task decomposition; speed distribution; singularity 收稿日期:2015-09-29 *基金项目:广东省教育部产学研结合项目(2012B091100145);广东省科技计划项目(2014A020208018) Foundation items: Supported by the Industry-Universities-Research Institutes Collaboration Project of Guangdong Province(2012B091100145) and the Science and Technology Planning Project of Guangdong Province(2014A020208018) 作者简介:张勤(1964-),女,博士,教授,硕士生导师,主要从事机器人及其应用系统研究.E-mail:zhangqin@scut.edu.cn 中图分类号:TP242 doi:10.3969/j.issn.1000-565X.2016.03.007