一种一阶连续分段曲线拟合方法*
段振云,王 宁,赵文辉,李 宁
(1.沈阳工业大学 机械工程学院,沈阳 110870;2.北方重工集团有限公司 输送设备分公司,沈阳 110141)
一种一阶连续分段曲线拟合方法*
段振云1,王宁1,赵文辉1,李宁2
(1.沈阳工业大学 机械工程学院,沈阳110870;2.北方重工集团有限公司 输送设备分公司,沈阳110141)
摘要:分段曲线拟合是一种常用的数据处理方法,但在分段点处拟合曲线往往不能满足连续性要求。提出一种一阶连续分段曲线拟合方法,即在确定每个拟合区间的原始数据个数之后,采用最小二乘法进行拟合,并在分段点处重复使用前一段末端数据,且对每段数据的起始点进行加权,使分段拟合曲线在分段点处更加逼近,减小拟合误差,根据拟合曲线重合部分的端点信息,采用三次Hermite插值的方法构造一条连接分段拟合曲线的插值曲线,使分段点处满足一阶连续,逐段处理,得到一条全局光滑连续的拟合曲线。将一阶连续分段曲线拟合方法应用于处理齿轮视觉检测中提取的齿廓边缘数据,证明拟合曲线在分段点处一阶连续,且拟合误差减小,易于编程实现。
关键词:分段拟合;分段点;加权;Hermite插值;一阶连续
0引言
在工程实践和科学实验中,常常需要对实验数据进行曲线拟合。例如应用机器视觉技术对齿轮进行测量时,根据边缘检测算法提取的齿轮边缘信息是一系列离散的数据点。为了提高边缘的测量精度,进一步降低随机噪声对边缘定位精度的影响,需要对提取的边缘点数据进行曲线拟合。最小二乘法是解决曲线拟合问题最常用的方法,根据最小均方差原则,可以有效得出最佳拟合函数[1]。
对于具有多个显著局部特征的数据,使用一个拟合函数来描述难以取得较好的拟合精度和效果,一般采用分段拟合的方法,在每段区间上进行局部最小二乘法拟合。然而,拟合函数在区间分段点上不一定连续,在相邻区间边界附近的拟合效果不理想[2-3]。
目前用于解决分段拟合曲线连续性问题的方法均存在局限性,有的是在选择分段点时,以每段拟合数据的最后一个点作为下一段拟合数据的起始点,这样并不能保证拟合曲线的连续性[4];有的只限于两个分段区间,对于具有多个分段区间的情况则不能处理[5];有的则是把全局连续性约束的分段拟合问题转化为带等式约束的误差最小化模型,通过拉格朗日乘数法推导出模型的最小二乘回归系数,这种方法的缺陷是不具有局部性,当分段数据中含有1个或多个误差数据时,会对最终拟合函数产生一定的影响[6]。
为了解决上述问题,提出一种一阶连续分段曲线拟合方法,以数据加权和三次Hermite插值为基础,对分段数据逐段进行拟合,实现拟合曲线的一阶连续性,减小拟合误差。
1分段拟合曲线连续性条件
由于使用最小二乘法对数据进行分段拟合可以更加准确地反映出数据点的整体分布状况,对于分段点处的数据进行加权,可以使分段拟合曲线在区间分段点处增进对数据点的逼近程度,减小分段点附近的拟合误差,使用Hermite插值的端点条件可以使分段拟合曲线在区间分段点处具有一阶连续性[7-9],因此提出一种一阶连续分段曲线拟合方法。
可用Beta约束定义分段拟合曲线的连续性,具体分析为:当存在实数βi(i=1,2,···,n),其中β1>0,使分段拟合曲线在分段点P的两侧导矢满足由方程(1)给出的一组Beta约束时,则称分段拟合曲线在分段点处具有Gn连续性。
(1)
由以上定义可知,若方程(1)中第一个方程成立,则P点为相邻分段拟合曲线的公共连接点,即有G0连续性。 若第二个方程也成立,即在分段点P处的一侧切矢是另一侧切矢的正数倍,表明相邻分段拟合曲线在该点具有G1连续性[10]。一阶连续分段曲线拟合算法用到的就是上述曲线的G0和G1连续性条件。
对于一组数据,首先对数据点进行分段,确定每次拟合所使用的原始数据点个数,并且前一段的最后一个数据点作为下一段的第一个数据点。分段完成之后,对第一段数据点进行最小二乘法拟合,拟合之后按一定的弧长将拟合曲线进行离散,得到一系列的离散点。对于第二段数据,取第一段拟合曲线的末端几个离散点和第二段原始数据共同构成,为了使分段拟合曲线在分段点处更加逼近,将第二段数据的起始点进行加权处理,即重复使用起始点多次,然后再进行最小二乘法曲线拟合,但这样处理之后仍然存在分段点处不连续的问题,因此将第二段拟合曲线也进行离散,使用两分段拟合曲线重合部分的端点信息,利用G0和G1连续性条件,进行三次Hermite插值,减小拟合曲线在分段点附近的偏离量,实现分段拟合曲线在分段点处的一阶连续,以此类推,逐段进行分段拟合和离散,并对数据进行加权处理,以插值曲线代替相邻拟合曲线的重合部分,使分段拟合曲线之间光滑连接,得到一条全局光滑连续的分段最小二乘法拟合曲线。
2一阶连续分段曲线拟合方法
已知数据可以表示为(xi,yi),i=1,2,3…n,采用一阶连续分段曲线拟合方法对数据进行处理。首先根据数据的分布特点,确定每段拟合曲线所用的原始数据个数为q1。按以下步骤对数据进行分段拟合。
(1)拟合函数一般为多项式函数,在一定范围内,连续函数可用多项式任意逼近,因此取第一段拟合数据为(xi,yi),i=1,2,3…q1确定拟合曲线的表达式f1(x)的形式为:
(2)
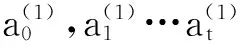
(2)将拟合后的曲线进行离散,若曲线的表达式为f1(x),设定离散弧长为s,则对于拟合曲线f1(x),以(x1,f1(x1))为起始点进行离散,得到离散点(xl1,yl1),l1=1,2,3…n1。
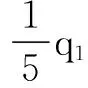
(4)同理,对于拟合曲线f2(x),以(xn1-4,f2(xn1-4))为起始点进行离散,得到离散点(xl2,yl2),l2=1,2,3…n2。
(5)对于得到的离散点数据(xl1,yl1),l1=1,2,3…n1和(xl2,yl2),l2=1,2,3…n2,其中(xl1,yl1),l1=n1-4,n1-3…n1和(xl2,yl2),l2=1,2,3…5是两段拟合曲线的重合部分,因此将这段数据用插值曲线表示,实现两分段拟合曲线的一阶连续。以(xn1-3,yn1-3)和(x4,y4)为插值曲线的两个端点,确定两分段拟合曲线连接部分插值曲线的形式为Q=α1x3+α2x2+α3x+α4,则其应当满足端点条件(即端点位置、端点的单位切向量),记
H(xj)=yj,H′(xj)=mj(j=0,1)
(3)
可以证明,满足插值条件(3)的三次Hermite插值函数是存在且唯一的[11]。
具体约束条件为:
(4)
通过约束条件(4),求出插值曲线的系数α1、α2、α3、α4,由于插值曲线在端点处一阶连续,因此可以实现两分段拟合曲线的光滑连接。
按照上述步骤,逐段进行处理,可以得到一条整体较为光滑且与所给数据点整体走势较为相符的连续曲线。
3实验分析
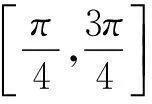
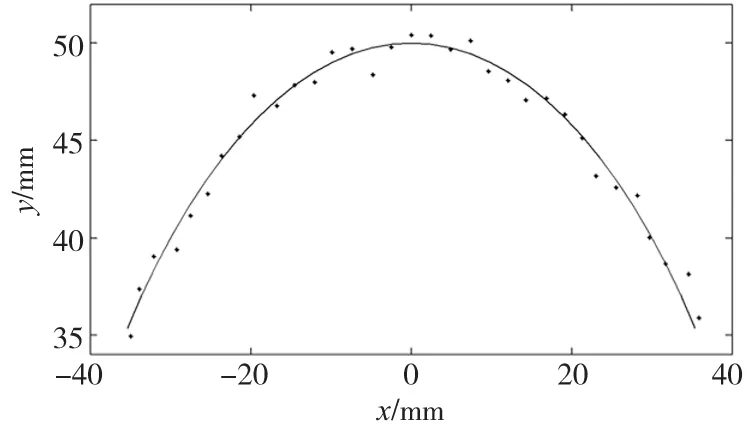
图1 数据样本点
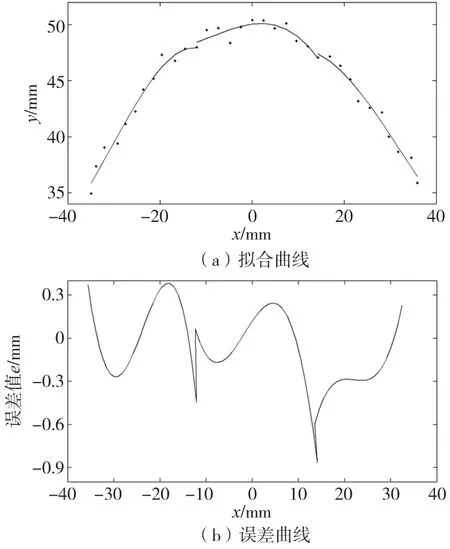
图2 独立曲线拟合
显然,与图2a相比,采用一阶连续分段曲线拟合方法所得的拟合曲线更加符合实际数据的连续性变化趋势,且没有带入畸变,保证拟合曲线形状的正确性。通过图2b和图3b的误差曲线,可以看出采用一阶连续分段曲线拟合方法比独立分段曲线拟合方法拟合误差小,在分段点处效果尤为突出,并且误差波动比独立分段曲线拟合方法波动小,拟合精度较高。
在应用机器视觉技术测量齿轮时,通过边缘检测算法提取齿廓边缘坐标点信息,其分布情况如图4a所示,为了更好地说明一阶连续分段曲线拟合方法的实用性,取局部边缘坐标点,如图4b所示,分别进行分段独立曲线拟合和一阶连续分段曲线拟合方法拟合。数据点为45个,将该边缘分为3段,每段使用原始数据15个,由于齿轮理论齿廓为渐开线,因此每个区间均采用三次函数进行拟合。图5为采用独立分段曲线拟合方法拟合,拟合曲线在分段点处的跳跃量为0.23像素,曲线不连续,这样会对齿轮测量造成一定的误差;图6为采用一阶连续分段曲线拟合方法拟合,拟合曲线在分段点处具有连续性,可以提高齿轮测量的精度。
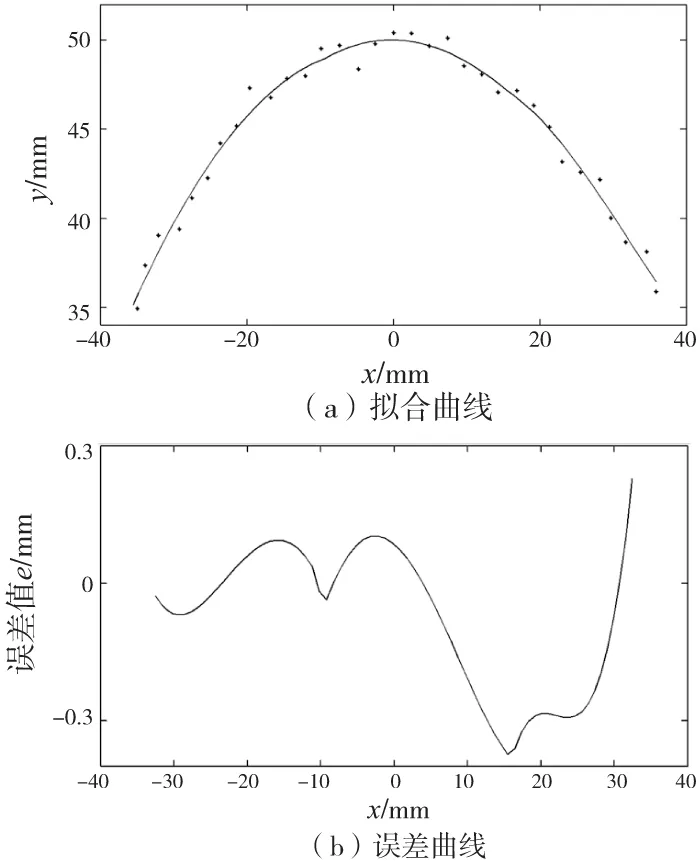
图3 一阶连续分段曲线拟合方法
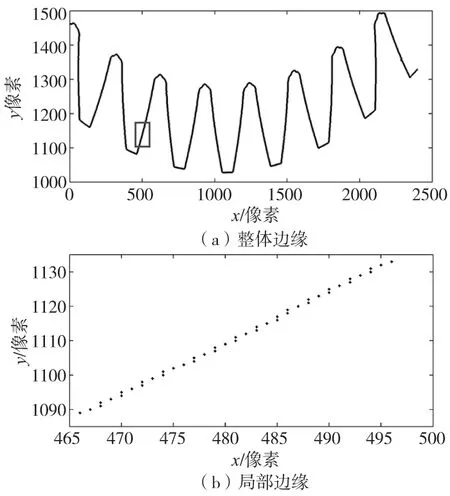
图4 齿轮边缘坐标点
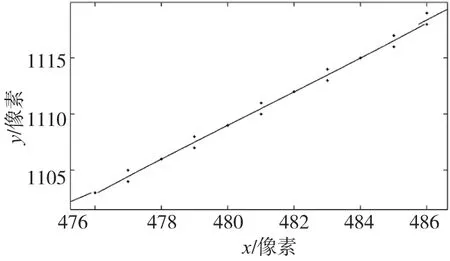
图5 独立曲线拟合
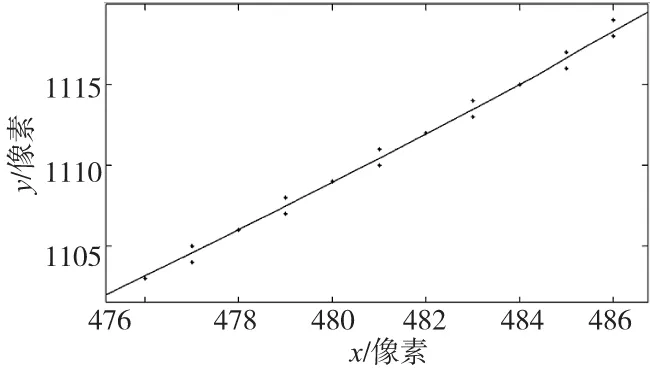
图6 一阶连续分段曲线拟合方法
4结论
针对分段曲线拟合时,分段点处不能满足连续性的问题,提出一种一阶连续分段曲线拟合方法,通过对起始点数据加权,并利用重合曲线的端点信息,构造一条连接分段拟合曲线的插值曲线,保证拟合曲线在分段点处具有连续性。实验证明,使用一阶连续分段曲线拟合方法进行曲线拟合时,可以保证拟合曲线在分段点处一阶连续,并且可以减小曲线拟合的误差,其效果在分段点处尤为明显,逐段对数据进行处理,可以得到一条全局光滑连续的拟合曲线,避免拟合曲线在分段点处的二义性,另外,本文方法易于编程实现,可以用于处理实验数据。
[参考文献]
[1] 李延芳. 基于协方差矩阵的轮廓曲线拟合算法研究[J]. 机械设计与制造, 2010(5):58-60.
[2] 王可, 唐忠辉, 孙兴伟. 一种点云数据曲线光顺处理算法[J].组合机床与自动化加工技术, 2013(2):64-69.
[3] Grama L, Rusu C. Phase approximation by divide-and-conquer piecewise linear fitting of gain[J]. International Symposium on Signals, Circuits and Systems, 2009: 1-4.
[4] 蔡山,张浩,陈洪辉,等. 基于最小二乘法的分段三次曲线拟合方法研究[J]. 科学技术与工程,2007,7(3):352-355.
[5] 刘晓莉,陈春梅.基于最小二乘原理的分段曲线拟合法[J].伊犁教育学院学报, 2004,17(3): 132-134.
[6] 侯超钧,曾艳姗,吴东庆,等.全局连续的分段最小二乘曲线拟合方法[J]. 重庆师范大学学报(自然科学版),2011, 28( 6): 44-48.
[7] 刘元朋,张定华,桂元坤,等. 用带约束的最小二乘法拟合平面圆曲线[J]. 计算机辅助设计与图形学学报,2004,16(10):1382-1385.
[8] 张龙飞, 檀结庆. 局部插值的H-Bezier曲线分段光顺拟合[J]. 合肥工业大学学报(自然科学版),2011,34(10):1570-1575.
[9] Ren-Hong Wang, Jing-Xin Wang.The poisedness of interpolation problem for splines[J]. Applied Numerical Mathematics, 2005(54):95-103.
[10] 李思, 高健. G1连续的封闭非均匀B样条曲线迭代算法[J]. 机械设计与制造, 2014(2):225-228.
[11] 彭爱清. 基于几何Hermite插值的曲线光顺研究[D]. 合肥:合肥工业大学,2012.
(编辑赵蓉)
Method of First-order Continuous Piecewise Curve-fitting
DUAN Zhen-yun1,WANG Ning1,ZHAO Wen-hui1,LI Ning2
(1. School of Mechanical Engineering, Shenyang University of Technology, Shenyang 110870,China;2. Transportation Eequipment Branch, Northern Heavy Industries Group Co., Ltd, Shenyang 110141,China)
Abstract:Piecewise curve-fitting is a commonly used processing method of data, but at sub-point fitting curve often does not meet the requirement for continuity.This paper present a method of first-order continuous piecewise curve-fitting. Firstly, The method determining the number of original data in each fitting interval, using piecewise curve-fitting to process data, and reusing data at the end of the previous period in the subsection point, weighting the starting point of each piece of data, which can make a piecewise fitting curve in the subsection point more approaching, and reduce the fitting error, according to the fitting curve overlapping part of the endpoint information, utilizing cubic Hermite interpolation to structure a interpolation curve that links the two piecewise fitting curves, making sub-point satisfy the first-order continuous, piecewise processing, getting a global smooth continuous fitting curve. The method of first-order continuous piecewise curve fitting is applied to process extracted tooth profile edge data in gear vision inspection, which proved that the fitting curve in the subsection point is first-order continuous, and fitting error is reduced, also it is easy to program.
Key words:piecewise curve-fitting; sub-point; weighting; Hermite interpolation; first-order continuous
文章编号:1001-2265(2016)05-0029-03
DOI:10.13462/j.cnki.mmtamt.2016.05.008
收稿日期:2015-06-28
*基金项目:十二五国家科技支撑计划(2014BAF08B01)
作者简介:段振云(1971—),男,河南新乡人,沈阳工业大学教授,博士生导师,博士,研究方向为复杂曲面加工技术、视觉检测,(E-mail)13604045543@139.com;通讯作者:王宁(1991—),女,辽宁大连人,沈阳工业大学博士研究生,研究方向为齿轮视觉检测,(E-mail)wangningcom@126.com。
中图分类号:TH161;TG506
文献标识码:A

