一个含有两个1-separation符号模式矩阵的最小秩*

龙佳平，邵燕灵

(中北大学 数学系，山西 太原 030051)



一个含有两个1-separation符号模式矩阵的最小秩*

龙佳平，邵燕灵

(中北大学 数学系，山西 太原 030051)

摘要:一个符号模式矩阵的最小秩指该符号模式矩阵定性类中实矩阵秩的最小值. 对于一个含有两个1-separation的符号模式矩阵，利用矩阵秩的性质，采用证明不等式的方法，给出了该符号模式矩阵最小秩的计算公式.

关键词:符号模式矩阵； 最小秩； 1-separation

0引言

一个符号模式矩阵(简称符号模式)是一个元素取自{+,-,0}的矩阵. 对于任意给定的实矩阵B=[bi,j]，B的符号模式是指一个以B中对应元素bi,j的符号为元素的矩阵，记为sgn(B). 一个m×n 符号模式A的定性类Q(A)，是所有满足sgn(B)=A的实矩阵B∈Rm×n的集合. 一个符号模式A的最小秩为mr(A)=min{rank(B)∶B∈Q(A)}.最近十几年，关于符号模式最小秩问题的一些新的结果不断由世界各地专家学者给出[1-5]. 2012年，LiZhongshan等得到了最小秩mr(A)≤2的符号模式矩阵A的一些特性[6]. 2014年，M.Arav等人利用与1-Separation相关联的某些广义符号模式的最小秩，得到了一个含有一个1-Separation的符号模式的最小秩的计算公式[7]. 广义符号模式的概念是通过允许符号模式中的某些元素为未定元扩展来的[8-11].

令

为一个符号模式，其中A1,1，a2,2，A3,3，a3,3，A5,5分别为m1×n1，1×1，m2×n2，1×1，m3×n3符号模式，称符号模式M含有两个1-Separation. 本文将给出M的最小秩的计算公式.

1有关结论

令1≤k,l≤m1,m2,m3,n1,n2,n3, 且k+l≤m2,n2，并令

分别为m1×n1，m2×n2和m3×n3的分块实矩阵，其中A2,2和B1,1为k×k方阵，B3,3和C1,1为l×l方阵，在文献[12]中介绍了A和B的k-子直和，记为A⊕kB. 这里定义A，B和C的k-l-子直和，记为A⊕kB⊕lC，为矩阵A⊕kB⊕lC=

引理 1[13]令

其中：C2,2和D1,1为k×k矩阵，则rank(C⊕kD)≤rank(C⊕D).

由以上引理，不难得出以下推论：

推论 1令

其中:C2,2和D1,1为k×k矩阵；D3,3和E1,1为l×l矩阵. 则有rank(C⊕kD⊕lE)≤rank(C⊕D⊕E).引理 2令

为一个符号模式. 其中：A1,1，A3,3，A5，5，a2,2，a4,4分别为m1×n1，m2×n2，m3×n3，1×1，1×1符号模式. 则下列不等式(1)～式(10)成立：

1) mr(A1,1)+mr(A3,3)+mr(A5,5)+4≥mr(M).

2) mr(A1,1)+mr([A3,3A3,4])+mr([A5,4A5,5])+3≥mr(M).

3) mr([A1,1A1,2])+mr([A3,2A3,3])+mr(A5,5)+3≥mr(M).

6)mr([A1,1A1,2])+mr([A3,2A3,3A3,4])+mr([A5,4A5,5])+2≥mr(M).

10) 对于任意的 p,q∈{+,-,0}，

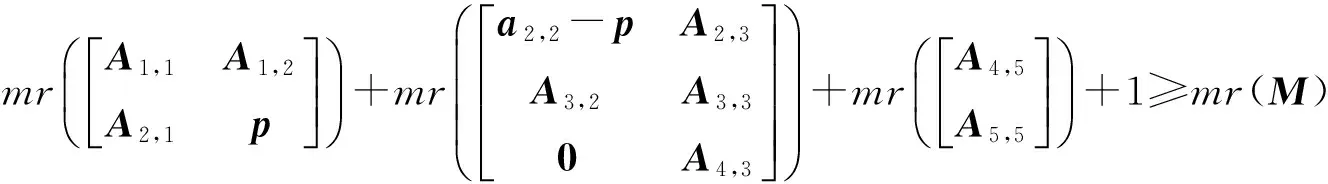
证明对于1)式，令C1,1∈Q(A1,1)，C3,3∈Q(A3,3)，C5,5∈Q(A5,5)，使得rank(C1,1)=mr(A1,1)，rank(C3,3)=mr(A3,3)，rank(C5,5)=mr(A5,5). 令C1,2∈Q(A1,2)，C2,1∈Q(A2,1)，C2,3∈Q(A2,3)，C3.2∈Q(A3,2)，C3.4∈Q(A3,4)，C4,3∈Q(A4,3)，C5,4∈Q(A5,4)，sgn(c2,2)=a2,2以及sgn(c4,4)=a4,4，则

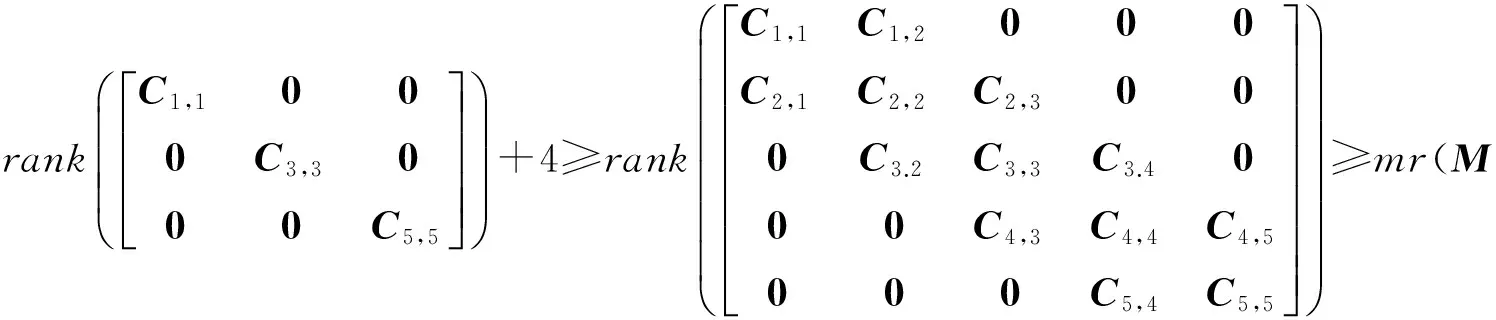
对于2)式，令

使得

显然，

式3)～9)的证明与式2)类似.

对于10)中最后一个不等式，令p,q∈{+,-,0}，令

并令

使得rank(C)=mr(Rp)，rank(D)=mr(Spq)和rank(E)=mr(Tq). 显然，C⊕1D⊕1E∈Q(M). 由推论1得mr(M)≤rank(C⊕1D⊕1E)≤

rank(C)+rank(D)+rank(E)=

剩余6个不等式的证明与式10)中最后一个不等式的证明类似.

2主要结果

定理 1令

为一个符号模式，其中A1,1，A3,3，A5,5，a2,2，a4,4分别为m1×n1，m2×n2，m3×n3，1×1，1×1符号模式. 对于任意的p,q∈{+,-,0}，令

则

证明设

则

(1)

因此，rank(PBQ)≥rank(B). 由矩阵秩的性质，rank(PBQ)≤rank(B)，故 rank(PBQ)=rank(B).

因而以下5种情形中的16个等式至少有一个成立：

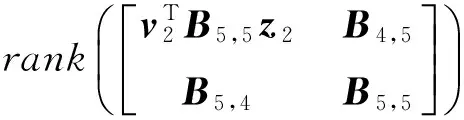
(2)由推论1可知不等式反过来同样成立，即式(2)为等式.

通过计算，我们可以得到P2B2Q2=

rank(B1,1)+rank(B2)+1=

(3)

类似地，E,H,F,G中仅有一个含有非零元，当存在0≠e∈E时，

(5)

(6)

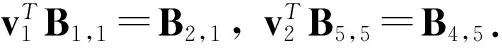
(7)

与情形2以及前面讨论类似地，可以得到以下5个式子：

当0≠e∈E和0≠f∈F时，

rank(B)=rank(B1,1)+

(8)

当0≠e∈E和0≠g∈G时，

(9)

当0≠f∈F和0≠g∈G时，

(10)

当0≠f∈F和0≠h∈H时，

(11)

当0≠g∈G和0≠h∈H时，

(12)

情形 4E,H,F,G中有3个含有非零元，不妨设0≠f∈F，0≠h∈H，0≠g∈G，则有以下式子成立

(13)

类似的3种情况分别有以下式子成立

rank(B)=rank(B1,1)+

(14)

(15)

rank(B)=rank(B1,1)+

(16)

情形 5E,H,F,G中都含有非零元，不妨设0≠e∈E，0≠h∈H，0≠f∈G，0≠g∈G，由矩阵的初等变换易得

rank(B)=rank(B1,1)+rank(B3,3)+

(17)

由引理3可知，定理结论中的等式左边小于等于右边成立，因而我们只需证明右边至少有一项等于左边.

令

使得rank(C)=mr(M).

由上面的讨论，我们将矩阵B替换成矩阵C，可以得到与以上5种情形中等式对应的16个类似的等式. 假设对应于情形3中式(9)

成立，则

rank(C)=mr(M).

对应于以上情形中式(5)～(7)、 式(10)～(14)的等式的证明，都与对应于情形3中式(9)证明类似.

对于与情形1中2)对应的等式的情况，由于

因此，

rank(C)=rank(M).

对于情形1至情形5中剩余等式的证明，都与情形1中2)对应的等式的情况类似.

参考文献:

[1]ForsterJ.Alinearlowerboundontheunboundederrorprobabilisticcommunicationcomplexity[J].JournalofComputerandSystemSciences, 2002, 65(4)： 612-625.

[2]BarioliF,FallatSM,HogbenL.Computationofminimalrankandpathcovernumberforcertaingraphs[J].LinearAlgebraanditsApplications, 2004, 392： 289-303.

[3]邵燕灵, 高玉斌. 非负不可约模式的最小秩[J]. 华北工学院学报, 2005, 26(1)： 6-10.

ShaoYanling,GaoYubin.Theminimumrankofnonnegativeirreduciblepatterns[J].JournalofNorthChinaInstituteofTechnology, 2005, 26(1)： 6-10. (inChinese)

[4]DeAlbaLM,HardyTL,HentzelIR,etal.Minimumrankandmaximumeigenvaluemultiplicityofsymmetrictreesignpatterns[J].LinearAlgebraanditsApplications, 2006, 418(2)： 394-415.

[5]BuC,WangW,SunL,etal.Minimum(maximum)rankofsignpatterntensorsandsignnonsingulartensors[J].LinearAlgebraanditsApplications, 2015, 483： 101-114.

[6]LiZ,GaoY,AravM,etal.Signpatternswithminimumrank2andupperboundsonminimumranks[J].LinearandMultilinearAlgebra, 2013, 61(7)： 895-908.

[7]AravM,HallFJ,LiZ,etal.Theminimumrankofasignpatternmatrixwitha1-separation[J].LinearAlgebraanditsApplications, 2014, 448： 205-216.

[8]高玉斌, 邵燕灵. 广义星符号模式的秩[J]. 数学研究与评论, 2005, 25(4)： 610-614.

GaoYubin,ShaoYanling.Ranksofgeneralizedstarsignpatterns[J].JournalofMathematicalResearchandExposition, 2005, 25(4)： 610-614. (inChinese)

[9]BarioliF,FallatSM,HallHT,etal.Ontheminimumrankofnotnecessarilysymmetricmatrices：apreliminarystudy[J].ElectronicJournalofLinearAlgebra, 2009, 18： 126-145.

[10]HogbenL.Anoteonminimumrankandmaximumnullityofsignpatterns[J].ElectronicJournalofLinearAlgebra, 2011, 22(1)： 202-213.

[11]HallF,LiZ.Signpatternmatrices,in：L.Hogben(Ed),HandbookofLinearAlgebra, 2ndedition,Chapman/HallCRCPress, 2013,Chapter42.

[12]FallatSM,JohnsonCR.Sub-directsumsandpositivityclassesofmatrices[J].Linearalgebraanditsapplications, 1999, 288： 149-173.

[13]BarioliF,BarrettW,FallatSM,etal.ParametersRelatedtoTree-Width,ZeroForcing,andMaximumNullityofaGraph[J].JournalofGraphTheory, 2013, 72(2)： 146-177.

The Minimum Rank of a Sign Pattern Matrix with Two 1-Separations

LONG Jia-ping, SHAO Yan-ling

(Dept. of Mathematics, North University of China, Taiyuan 030051, China)

Abstract:The minimum rank of a sign pattern matrix is the smallest value among all real matrices ranks belong to the qualitative class of the sign pattern matrix. For the sign pattern matrix that has two 1-separations, the formula to compute the minimum rank of the sign pattern matrix is presented by the properties about the matrix rank and the methods of proving inequality.

Key words:sign pattern matrix; minimum rank; 1-separation

文章编号:1673-3193(2016)02-0112-08

*收稿日期:2015-08-10

基金项目：国家自然科学基金项目(11071227)

作者简介：龙佳平(1992-)，男，硕士生，主要从事组合数学研究.

中图分类号:O157

文献标识码:A

doi:10.3969/j.issn.1673-3193.2016.02.004