Hilbert—Huang变换提取齿轮箱故障特征方法研究

张志斌+王菁+宋晓菲

摘 要：本文在研究了Hilbert-Huang变换的原理和它在非线性、非平稳信号分析中的独特优势的基础上，重点研究了利用经验模态分解和Hilbert-Huang变换提取齿轮箱故障特征的方法，实验证实，通过对齿轮箱的振动信号进行经验模态分解，并对分解得到的IMF分量进行包络谱分析，能够准确实现对齿轮箱内齿轮的故障定位。

关键词：Hilbert-Huang变换；经验模态分解；齿轮箱；故障诊断

DOI：10.16640/j.cnki.37-1222/t.2016.12.008

1 Hilbert-Huang变换简介

Hilbert-Huang变换（简称HHT）是Norden E.Huang等人于1998年首次提出的一种新的信号分析理论。Hilbert-Huang变换应用经验模态分解（Empirical Mode Decomposition 或EMD）理论将信号分解成相互独立的若干固有模态（Intrinsic Mode Function 或IMF）的和，并对每个IMF进行Hilbert变换得到信号的瞬时频率和幅值，从而给出信号随时间和频率变化的精确表达，因而可以用于对信号的局部行为做出精确的描述。

对任一实信号s（t）进行EMD，直至分量cn（t）或剩余信号rn（t）足够小时或剩余信号cn（t）变成一个单调函数，以至不能再从中提取IMF时终止分解，可以得到：。

构造解析函数zi（t）=ci（t）+jH[ci（t）]，其中：，这样，就可以把信号s（t）展开成（Re表示取实部），其中：，。于是得到信号s（t）的Hilbert谱及其边界谱。

2 基于Hilbert-Huang变换的齿轮箱故障特征提取

单级传动的齿轮箱输入轴齿轮齿数为28，输出轴齿轮齿数为36， 电机转速为1473r/min，输入轴回转频率为24.55Hz，输出轴回转频率为为19.11Hz，齿轮啮合频率为688Hz。在从动轴齿轮齿根处加工宽0.1mm、深3mm的小槽以模拟齿根裂纹。测量得到的振动信号及其功率谱如图1所示。

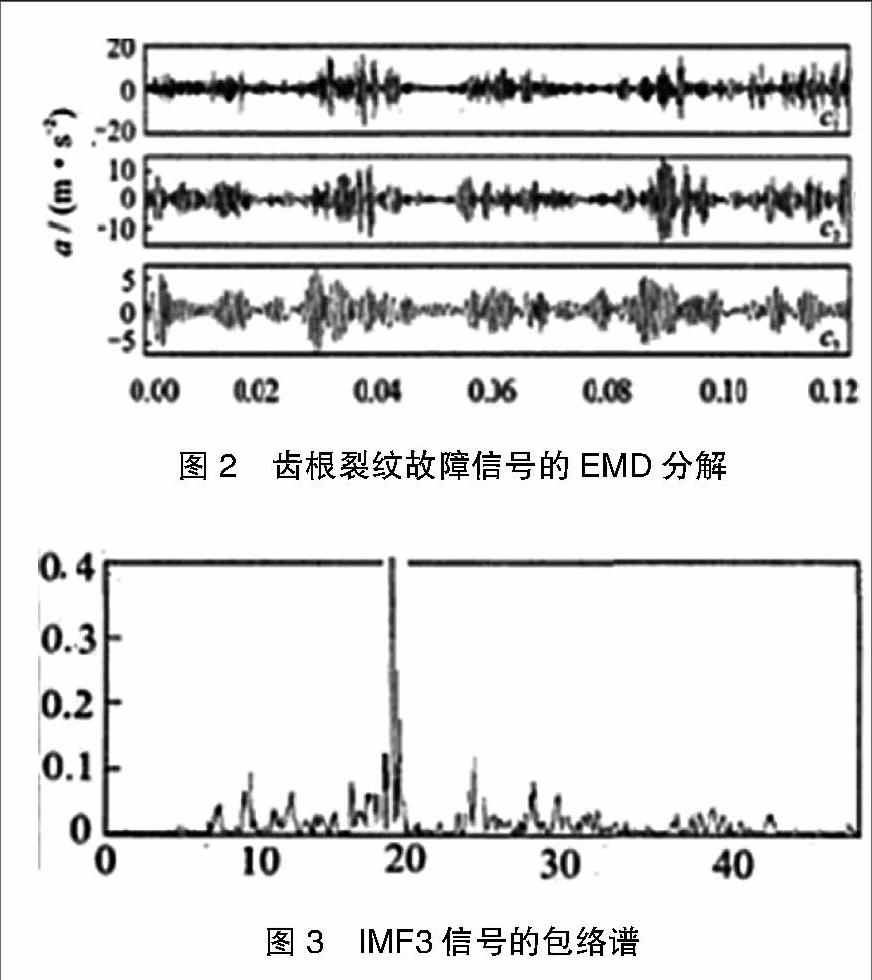
从功率谱图中能找到啮合频率及其二倍频，但没有边带信息，因此难以判断故障发生的部位。将振动信号进行EMD分解，进而可以得到IMF信号的包络谱，图2所示即为EMD分解得到的9个分量中的前3个。图3为IMF3信号的包络谱，可以很清晰地看到故障齿轮所在的输出轴的频率特征。

参考文献：

[1]N.E.Huang， The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-stationary Time Series Analysis， J. Proc. R. Soc. Lond. A， 1998， 454：903-995

[2]张志斌.基于频响修正的齿轮箱故障诊断研究[D].石家庄：军械工程学院，2004.

[3]uang NE， Wu ML， Long SR， et al. A confidential limit for the empirical mode decomposition and Hilbert spectrum analysis [J].eedings of the Royal Society of London. A （2003），459：2317-2345.