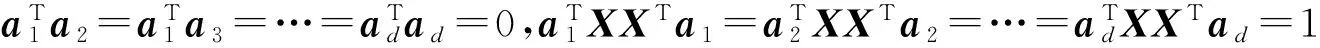基于随机投影的正交判别流形学习算法

马　丽，　董唯光，　梁金平，　张晓东

(兰州交通大学 自动化与电气工程学院　甘肃 兰州 730070)



基于随机投影的正交判别流形学习算法

马丽，董唯光，梁金平，张晓东

(兰州交通大学 自动化与电气工程学院甘肃 兰州 730070)

摘要：提出一种基于流形距离的局部线性嵌入算法，以流形距离测度数据间的相似度，选择各样本点的近邻域，解决了欧氏距离作为相似性度量时对邻域参数的敏感性.在MDLLE算法中引入最大边缘准则(maximum margin criterion,MMC)来构建最优平移缩放模型，使得算法在保持LLE局部几何结构的同时，具有MMC准则判别能力.通过正交化低维特征向量可消除降维过程中的噪声影响，进而提高算法的监督判别能力.由实验结果得到,所提出的方法具有良好的降维效果，能有效避免局部降维算法对邻域参数的敏感.随机投影独立于原始高维数据，将高维数据映射到一个行单位化的随机变换矩阵的低维空间中，维持映射与原始数据的紧密关系，从理论上分析证明了在流形学习算法中采用随机投影可以高概率保证在低维空间保持高维数据信息.

关键词：流形学习算法； 邻域选择； 流形距离； 正交判别； 局部线性嵌入； 随机投影

0引言

在当今的信息社会中，人们获得数据和信息的能力越来越强.而这些数据信息呈现出的特性是高维数、大规模和结构复杂等.那么如何从这些繁杂的数据中迅速提取有价值的信息，引起了人们的关注和研究.因此，数据的维数约简就显得尤为重要了.数据降维，一方面可以解决“维数灾难”，缓解“数据爆炸但知识贫乏”的现状[1]，降低复杂度；另一方面可以更好地认识和利用数据.

流形学习用于数据维数约简，已成为数据挖掘的研究热点.假设数据是均匀采样于一个高维观测空间中的低维流形，流形学习就是从高维采样数据中恢复这个低维流形结构[2]，并求出相应的低维嵌入映射，以实现数据降维或数据可视化.它是从观测到的现象中去寻找事物的本质，找到复杂数据的内在规律.近年来，流形学习邻域已取得了大量的研究成果.经典的非线性流形学习算法有等距特征映射算法(isometric map, isomap)[1]、局部线性嵌入算法(locally linear embedding, LLE)[2]、Laplacian 特征映射算法(Laplacian eigenmaps, LE)[3]、Hessian 特征映射算法(Hessian-based locally linear embedding, HLLE)[4]、局部切空间排列算法(local tangent space alignment, LTSA)[5]和黎曼流形学习算法(Riemannian manifold learning)等.现有的流形学习算法根据所保持几何特性的不同，可分为局部特性保持算法和全局特性保持算法.局部特性保持算法主要是保持流形的局部几何结构特性，通过映射建立高维观测空间与低维流形之间的联系，在低维流形空间中保持近邻域所具有的局部结构.全局特性保持算法主要是保持低维流形的全局几何结构，构造所有数据点对之间的全局度量矩阵，再将度量矩阵转化为内积矩阵并求解其特征向量，即可获得数据集的内在低维结构.目前，很多研究者对上述经典算法进行改进，如有监督的流形学习算法[3]、增量式流形学习算法等[6—7]，显著提高了原始算法的性能.

针对局部降维算法中近邻参数K的选取问题，很多研究者提出了自适应选择近邻算法[8—11].文献[12]通过分析数据集中任意样本所在局部区域的线性重构误差，确定该局部区域的近似线性块，然后根据位于此局部线性块上的样本数来自适应地选择局部线性嵌入的近邻参数K.文献[13]提出的邻域参数动态变化的局部线性嵌入算法，根据测地距离与欧氏距离的关系动态确定数据点的邻域.该方法能获得较好的效果，但计算复杂度较高，在处理非均匀分布的数据流形时，欧氏距离作为相似性度量无法反映样本的全局一致性，而流形距离[14]能有效反映样本固有的全局一致性信息.故本文提出一种基于流形距离的局部线性嵌入算法(locally linear embedding algorithms based on manifold distance, MDLLE)，通过流形距离作为样本间相似性度量的测度，对空间分布复杂的流形结构的数据具有更好的性能.

随机投影[15—17]是维数约简中出现的一种新方法，尤其Johnson-Lindenstrauss (JL)引理[16]给出了一个重要的结论，利用随机投影可将N维欧氏空间中包含任意n个点的集合映射到K维的欧氏空间(K≪N)，并且能以较高的概率保持原空间中任意两点间距离变化极小.也就是说，可以随机选择一个适当的高维子空间(需比原始空间维度小)，原始空间两点间的距离投影到这个子空间，能高概率地保持这种距离关系.本文用理论证明了随机投影保持原始数据信息的有效性，在LLE算法中采用随机投影实现从高维空间到低维空间的映射，以较高的概率保证投影后数据点之间的距离信息变化不大.

1局部线性嵌入算法

局部线性嵌入算法[2]是一种局部特性保持方法，核心是保持降维前后近邻之间的线性结构不变.其前提假设是高维数据所在的低维流形是局部线性的，即每个样本点可以用其近邻点线性表示.算法的主要思想是通过在低维嵌入空间中保持每个数据点的近邻重构系数来保持整个数据的流形结构，即以重构权值矩阵作为高维观测空间与低维嵌入空间的联系桥梁：高维观测空间的每个数据点用其近邻点线性表示的权重与它们在低维嵌入空间中线性表示的权重保持一致.由于流形上的局部可以认为是一个局部欧式空间，因此每个样本点与其近邻样本之间是线性关系，从而一个样本可以用其近邻样本的线性组合来重构.

LLE算法包含以下3个基本步骤：

1) 构造近邻域.对于给定的数据集X=[x1,x2,…,xn]∈RD×n，在高维数据空间，通过欧氏距离寻找与每个样本点最近的k个近邻，xi的k个近邻集合为N(xi)={xi1,xi2,…,xik}.

2) 计算高维空间中的局部线性表示.权值矩阵W 对于每个样本点xi及其近邻集N(xi)={xi1,xi2,…,xik},是通过最小二乘法极小化每个样本点的重构误差得到，即：

其中:权值wij反映了样本点xj对xi重构的贡献.

3) 求低维嵌入Y.在低维空间用各个样本点的近邻重构其本身，即求Y=[y1,y2,…,yN]，使得重构误差最小，设置误差函数为：

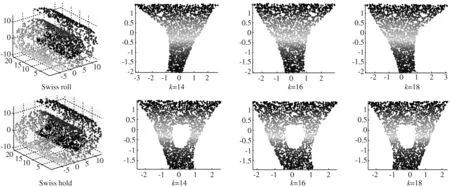
图1　LLE算法的降维效果Fig.1　Reduction-dimensional effect of LLE

2基于流形距离的局部线性嵌入

2.1流形距离

由于数据集的低维流形分布，用欧氏距离来选择最近邻域时，这些选择的近邻点不能准确地表征流形上的真正邻域结构.为了解决流形上数据的最近邻点的选择，提出一种新的相似度度量来计算数据点间的最短距离.

定义1流形上两点xi,xj的线段长度定义为：

(1)

其中：d(xi,xj)表示xi,xj之间的欧氏距离，τ是可调参数.

(2)

其中：L(a,b)表示两点间流形上的线段长度.流形距离满足以下4个条件：

1) 对称性：MD(xi,xj)=MD(xj,xi)；

2) 非负性：MD(xi,xj)≥0；

3) 三角不等式：对任意的xi,xj,xk，有MD(xi,xj)≤MD(xi,xk)+MD(xk,xj)；

4) 自反性：MD(xi,xj)=0，当且仅当xi=xj.

两个数据点间的距离越小，它们的相似度越高.因此，定义xi,xj间的相似度为：

(3)

需说明的是，本文定义样本自身的相似度为0，即当i=j时，σij=0.

2.2基于流形距离的邻域选择

当数据集不满足全局线性结构时，用欧氏距离度量数据间的相似度，选取近邻点是不合理的.而流形距离测度满足上述的自反性、非负性、对称性及三角不等性，故使用流形距离可以反映空间分布复杂的流形数据[18].如图所示，图2是用欧氏距离作为测度所选的近邻点，图3是用流形距离作为测度所选的近邻点，图中黑色实心点X、Y为样本点，以X、Y为中心的近邻域由虚线圆画出.相同流形上两点间的距离较短，不同流形上两点间的距离较长，从图上可以观察到以流形距离为测度给样本点X、Y选出的近邻点更合理.图4中S型曲线上有两点M、N分别用流形距离和欧氏距离选出其近邻域，如图所示以流形距离作为测度所选的近邻域用实线画出，以欧氏距离作为测度所选的近邻域用虚线画出，当曲率较大时采用欧氏距离选出的近邻域不能反映流形的局部结构，而基于流形距离的近邻域选择可以很好地反映流形的局部结构.

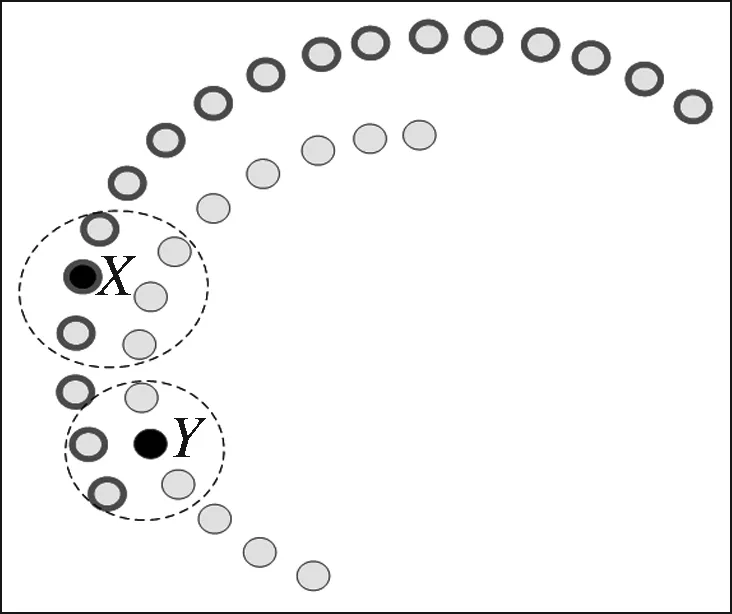
图2　以欧氏距离所选的近邻点Fig.2　Neighbors selected by Euclidean

图3　以流形距离所选的近邻点Fig.3　Neighbors selected by manifold

图4　S型曲线上样本点的近邻选择Fig.4　Neighbors selected on the S curve

根据上述定义，可以计算数据集中任意两点间的流形距离，然后选择合适的邻域.算法流程如下.

步骤1利用K最近邻算法的思想，由式(1)构建线段长度矩阵L；

步骤2利用式(2)计算数据点对之间最短的路径，得到流形距离，并根据式(3)计算数据点对间的相似度.

步骤3根据步骤2 计算出的点对间的相似度选择样本点xi的最近邻点得到近邻点数.

2.3基于流形距离的局部线性嵌入算法

用流形距离代替欧氏距离计算.假设数据样本集X=[x1,x2,…,xn]∈RD×n，根据2.2节描述的算法计算线段长度矩阵L，进而求出流形距离MD.使用流形距离作为相似度度量构造算法的目标函数，并求出各个样本点xi的K个近邻点xi1,xi2,…,xik.对任意样本点xi，用其近邻点的线性组合重构xi，使得误差函数在流形距离度量下最小.在低维空间用各个样本点的近邻重构其本身，即求Y=[y1,y2,…,yN]，使得重构误差最小.

用流形距离表示权值矩阵W：

根据欧氏距离下定义的权值系数，可得：

故可将流形距离下的权值矩阵表示为：

在低维空间中用流形距离表示的权值矩阵计算低维嵌入Y，使其重构误差最小，则重构误差函数为：

构造目标函数，如下：

(4)

约束条件：ATXMXTA=I.

由于随机投影在降维后能很好地保持原高维数据的主要特性，因此在MDLLE算法从高维到低维映射的过程中采用随机投影，建立足够多的随机映射算子，保证在降维过程中高概率地保持原始数据信息.

3随机映射定理

这个定理说明，对于任意一个样本大小为m的集合，如果通过随机投影将其维度降到一个合适的范围内，那么将以较高的概率保证投影后数据点之间的距离信息变化不大.因此，在LLE算法中用随机投影将流形距离投影到低维空间，保证了投影后数据点间的距离信息不发生太大变化.在MDLLE算法中要保持不变的是近邻点之间的流形距离，通过随机映射算子Φ:RN→RM，将流形距离高概率地投影到M维的随机子空间中，这样就使得高维观测空间中流形数据的局部结构在低维空间得到保持.

从定理1可以得到:

即随机投影后高概率保持近邻点之间的流形距离.

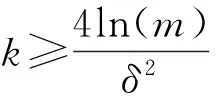
(5)

(6)

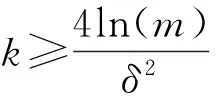
随机投影的思想来源于Johnson-Lindenstrauss (JL)[19—21]引理,假如一个向量空间中的点被映射到一个适当高维的随机子空间中，那么这种映射会近似地维持映射点之间的距离.相关的证明参见文献[20—21].随机投影之所以精确重建原始数据的关键在于随机投影矩阵H满足一定阶数的限制等距条件(RIP)：

随机映射算子Φ:RN→RM要满足K阶的限制等距条件RIP，K

在光滑K维子流形μ⊂RN上，存在随机映射算子Φ:RN→RM，(K

(7)

(8)

根据式(6)～(7)可以推导：

(9)

由此证明了随机投影降维后在低维空间能保留高维观测空间中的数据信息.即用随机映射变换可以在低维空间维持高维数据近邻之间的流形距离.

4正交判别

4.1引入监督

MMC是通过最大化类间平均边缘求取最优线性子空间[22].MMC算法的目标函数可以表示为：

J(W)=tr{WT(Sb-Sw)W},

式中Sw和Sb分别表示样本的类内散度矩阵和类间散度矩阵.

在MDLLE算法中引入MMC来构建最优平移缩放模型，使得算法在保持LLE局部几何结构的同时，具有MMC判别能力.通过正交化低维特征向量可消除降维过程中的噪声影响，进而提高算法的监督判别能力.故提出一种有监督的MDLLE算法.因此，上述目标函数(4)可描述成如下优化问题：

(10)

对式(10)进行线性变换：

min tr{AT(XMXT-(Sb-SW))A}s.t.ATXXTA=I.

运用Lagrangian算子求解上述优化问题，得：

上式的求解就转化为如下广义特征值的求解：

(XMXT-(Sb-Sw))a=λXXTa，

(11)

式中:λ是广义特征方程(11)的特征值，a是其特征值对应的特征向量.由广义特征方程(11)可知，当线性变换矩阵A是由广义特征对{(XMXT-(Sb-Sw)),XXT}的前d个最小特征值对应的特征向量组成时，目标函数将取得最小值.

4.2特征向量正交化

由于所求解的特征向量是非正交的，因此需将特征向量正交化，以消除噪声影响,最终将所要求解的低维度特征向量转化为矩阵特征值的求解问题[23].这里采用一种新的正交化方法.令Q=XMXT-(Sb-Sw)，算法的目标是要寻找一组正交基向量a1,a2,…,ad.极小化如下目标函数，并获取第k个正交基向量：

(12)

运用Lagrangian算子求解式(12)，得：

则有：

2Qak-2λXXTak-η1a1-…-ηk-1ak-1=0.

(13)

将式(13)左乘(XXT)-1，得：

2(XXT)-1Qak-2λXXTak-η1(XXT)-1a1-…-ηk-1(XXT)-1ak-1=0,

即所求的正交基向量{a1,a2,…,ad}就是最小特征值λ所对应的特征向量.所求的正交基向量可完全避免约简后的低维局部子空间的结构失真，具有稳定的局部分类判别力，故引入正交后比LLE有更好的分类精度.

基于随机投影的正交判别流形学习算法步骤.

步骤1生成随机投影变换矩阵H：各行均是单位化的独立同分布零均值正态变量的标准正交矩阵.

步骤2构建M个随机映射算子Φ:RN→RM.

步骤4用随机映射算子Φ:RN→RM，将权值矩阵高概率地投影到低维空间.

步骤5在低维空间中用正交化的低维特征向量进行优化判别：求解方程(XMXT-(Sb-Sw))a=λXXTa的特征值λ及其特征向量a1,a2,…,ad.

5实验仿真

1) 为了验证MDLLE算法的性能，本文采用经典实验数据集Swiss roll和Swiss hold来说明本文提出的算法能够有效地处理非线性流形数据集.数据集的采样点数N=2 000，分别选取邻域参数k=14、k=16、k=18.图1所示为LLE算法对数据集Swiss roll的降维，从图中可以看出当邻域参数k不同时，LLE算法的降维效果表现出不稳定性，即LLE算法无法正确揭示原始数据的低维结构，降维后的低维结果发生严重变形.图5所示为MDLLE算法对数据集Swiss roll和Swiss hold的降维，从图中可以看出当邻域参数k不同时，MDLLE算法所揭示的低维结构可以良好地展现原始数据集的本质低维结构，即在一定的范围内，MDLLE算法对邻域参数不敏感，改善了原始算法的降维效果.

2) 为了验证监督性MDLLE算法的性能，实验将监督MDLLE、MDLLE及LLE进行比较.随机选择YALE人脸图库中的图像作为训练样本，3种算法在相同训练样本和测试样本下运行20次，取其平均识别结果作为每种算法的识别结果.YALE图库中有15个人，每人在不同表情和不同光照下有11张图像，图6为YALE图库中1个人的样本图像.随机选择3、6、9张图像作为训练样本集，其余为测试样本集.实验结果如表1所示，显示了20次重复实验的最大平均识别率.从表中可以看出有监督的算法MDLLE具有更好的识别精度.随着训练次数的增多，算法LLE、MDLLE、监督型MDLLE对人脸图像的识别精度也提高了.由于监督型MDLLE算法引入MMC构建最优平移缩放模型，使得算法在保持局部几何结构信息的同时具有监督判别能力，因此算法对人脸图像的分类识别精度得到了很大的提高.

图5　MDLLE算法的降维效果Fig.5　Reduction-dimensional effect of MDLLE

图6　YALE 人脸库图像示例Fig.6　Sample face images from the YALE database

表1　YALE人脸图库上算法性能比较

6结论

本文针对局部线性嵌入算法中邻域参数选择问题，提出了一种基于流形距离的局部线性嵌入算法(MDLLE)，该算法用流形距离代替传统的欧氏距离作为相似性度量，利用流形距离测度合理地选取各个样本的近邻点，实现了高维数据的降维.实验结果表明，本文提出的基于流形距离的近邻选择算法可以有效避免局部降维算法对选取近邻参数K的不确定性.在MDLLE算法中引入最大边缘准则，通过正交化低维特征向量消除降维过程中的噪声影响，提高算法的监督判别能力，有监督的MDLLE算法在实验中具有较好的降维性和稳定性，提高了图像识别精度.从理论上证明了随机投影能够很好地保持流形数据上的主要特征，随机投影在流形学习算法的降维中还有很大的研究空间.在后续的研究中将通过仿真实验证明随机投影在其他流形学习算法降维中的优势，并讨论随机投影与流形本征维数之间的关系.

参考文献：

[1]ROWEIS S, SAUL L. Nonlinear dimensionality reduction by locally linear embedding [J]. Science, 2000, 290(5500): 2323—2326.

[2]TENENBAUM J B, SILA A V, LANGFORD J C. A global geometric framework for nonlinear dimensionality reduction [J]. Science, 2000, 290(5500): 2319—2323.

[3]孟德宇, 徐宗本, 戴明伟. 一种新的有监督流形学习方法[J]. 计算机研究与发展, 2007, 44(12): 2072—2077.

[4]DONOHO D L, GRIMES C. Hessian eigenmaps: locally linear embedding techniques for high-dimensional data [J]. Proc eedings of the national academy of sciences of USA, 2003, 100(10): 5591—5596.

[5]ZHANG Z Y, ZHA H Y. Principal manifolds and nonlinear dimension reduction via local tangent space alignment [J]. SIAM journal： scientific computing, 2005, 26(1): 313—338.

[6]李峰, 田大庆, 王家序. 基于有监督增量式局部线性嵌入的故障辨识[J]. 振动与冲击，2013, 32(23): 82—88.

[7]LAW M H C, JAIN A K. Incremental nonlinear dimensionality reduction by manifold learning [J]. IEEE transaction on pattern analysis and machine intelligence, 2006, 28(3): 377—391.

[8]ZHANG Z Y, WANG J, ZHA H Y. Adaptive manifold learning[J]. IEEE transaction on pattern analysis and machine intelligence, 2012, 34(2): 253—265.

[9]侯越先, 吴静怡. 基于局域主方向重构的适应性非线性维数约简[J]. 计算机应用，2006, 26(4): 895—897.

[10] 蒲玲. 自适应局部线性降维方法[J]. 计算机应用与软件, 2013, 30(4): 255—257.

[11] 蒲玲. 自适应邻域图的流形学习方法[J]. 计算机应用与软件, 2014, 31(2): 191—194.

[12] 惠康华, 肖柏华, 王春恒. 基于自适应近邻参数的局部线性嵌入[J].模式识别与人工智能, 2010, 23(6): 842—846.

[13] 文贵华, 江丽君, 文军. 邻域参数动态变化的局部线性嵌入[J]. 软件学报, 2008, 19(7): 1666—1673.

[14]MA J J, GONG M G, JIAO L C. Evolutionary clustering algorithm based on mixed measures [J]. International journal of intelligent computing and cybernetics, 2011, 4(4): 511—526.

[15]SOOMIN LEE, ANGELIA N. Distributed random projection algorithm for convex optimization [J]. IEEE J Sel Topics Signal Processing, 2013, 7(2): 221—229.

[16]SANJOY D, ANUPAM G. An elementary proof of the JL lemma: technical report TR-99-006 [R]. University of California, Berkeley, 1990.

[17]HEGDE C, WAKIN M B, TENENBAUM J. Random projection for manifold learning proofs and analysis: technical report TREE 0710 [R]. Rice University,Houston,2007.

[18]魏莱, 王守觉. 基于流形距离的半监督判别分析[J]. 软件学报, 2010, 21(10): 2445—2453.

[19]RICHARD G, BARANIUK, MICHAEL B W. Random projections of smooth manifold[J]. Foundations of computational mathematics, 2009, 9(1): 51—77.

[20]DASGUPTA S, GUPTA A. An elementary proof of the Johnson-Lindentrauss lemma: technical report TR-99-006 [R]. International Computer Science Institute, Berkeley, California, 1999.

[21]FRANKL P, MAEHARA H. The Johnoson-Lindenstrauss lemma and the sphericity of some graphs[J]. Journal of combinatorial theory: Ser. B, 1988, 44: 355—362.

[22]袁暋, 程雷, 朱然刚. 一种新的基于MMC和LSE的监督流形学习算法[J]. 自动化学报, 2013, 39(12): 2077—2089.

[23]张光耀，李镇.一个n*n矩阵特征值问题的迹公式及其应用[J]. 郑州大学学报(理学版)，2010，,4(4)：18—23.

(责任编辑：王浩毅)

Manifold Learning Algorithms of Orthogonal Discriminant Based on Random Projection

MA Li,DONG Weiguang, LIANG Jinping, ZHANG Xiaodong

(DepartmentofAutomationandElectricalEngineering,LanzhouJiaotongUniversity,Lanzhou730070,China)

Abstract:A kind of locally linear embedding algorithms based on manifold distance, MDLLE was proposed. The similarity between data can be could measured based on the manifold distance and the neighbor domain of the sample points can be selected. This could solve the neighborhood parameter sensitivity of the Euclidean distance in similarity measure. The maximum margin criterion(MMC) is introduced in the MDLLE algorithm for constructing the optimal translation and scaling model. Thus, the algorithm both can both maintain local geometric structure of LLE and have discriminant ability of Maximum margin criterion. The low-dimensional feature vector of orthogonalization can eliminate noise effects in the process of dimension reduction, and improve the supervision and discriminant ability of the algorithm. The experimental result showed that this method had good dimension reduction effect and can effectively avoid sensitivity. Random projection is independent of the original high-dimensional data, which mapped the high-dimensional data to a low-dimensional space of the random transformation matrix of line normalized. The theoretical analysis proved that the manifold learning algorithm of taking random projection could maintain high-dimensional data in low-dimensional space in high probability.

Key words:manifold learning； neighborhood selection； manifold distance； similarity measure； locally linear embedding； random projection

收稿日期:2015-08-21

基金项目:甘肃省科技支撑基金资助项目(1204GKCA038)；甘肃省财政厅基本科研业务费资助项目(213063).

作者简介:马丽(1990—)，女，甘肃兰州人，硕士研究生，主要从事非线性数据降维研究,E-mail:mary15117221064@163.com.

中图分类号：TP181

文献标志码：A

文章编号：1671-6841(2016)01-0102-08

DOI:10.3969/j.issn.1671-6841.201508008

引用本文：马丽，董唯光，梁金平，等.基于随机投影的正交判别流形学习算法[J].郑州大学学报(理学版)，2016,48(1)：102—109