一种基于决策树的多示例学习算法
王 杰, 蔡良健, 高 瑜
(1. 郑州大学 电气工程学院 河南 郑州450001; 2. 郑州大学 信息工程学院 河南 郑州 450001)
一种基于决策树的多示例学习算法
王杰1, 蔡良健1, 高瑜2
(1. 郑州大学 电气工程学院河南 郑州450001; 2. 郑州大学 信息工程学院河南 郑州 450001)
摘要:提出了一种基于决策树 C4.5 的多示例学习算法 C4.5-MI,通过拓展 C4.5的熵函数和信息增益比来适应多示例学习框架.应用梯度提升方法对 C4.5-MI算法进行优化,得到效果更优的GDBT-MI算法.与同类决策树算法在benchmark数据集上进行比较,结果表明,C4.5-MI 和 GDBT-MI 算法具有更好的多示例分类效果.
关键词:多示例学习; 决策树; 梯度提升; C4.5算法
0引言
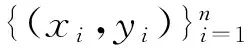
1决策树及 C4.5算法
决策树的主要优点是模型具有可读性, 分类速度快, 应用广泛. 学习时, 利用训练数据, 根据损失函数最小化的原则建立决策树模型;预测时, 对新的数据利用决策树模型进行分类.C4.5 是 ID3 扩展版, 它既可以处理连续和离散的量,也可以处理带有缺失数据的数据集,分类效果比 ID3 更优.
C4.5 的生成算法[7]如下:
输入:训练数据集D, 特征集A, 阈值ε; 输出:决策树T.
Step 1如果D中所有示例属于同一类Ck, 则置T为单节点树, 并将Ck作为该节点的类, 返回T.
Step 2如果A=∅ , 则置T为单节点树, 并将D中示例数最大的类Ck作为该节点的类, 返回T.
Step 3否则, 计算A中各特征对D的信息增益比, 选择信息增益比最大的特征Ag.
Step 4如果Ag的信息增益比小于阈值ε, 则置T为单节点树, 并将D中示例数最大的类Ck作为该节点的类, 返回T.
Step 5否则, 对Ag的每一可能值ai, 依Ag=ai将D分割为若干非空子集Di, 将Di中示例数最大的类作为标记, 构建子节点, 由节点及其子节点构成树T, 返回T.
Step 6对节点i, 以Di为训练集, 以A-{Ag} 为特征集, 递归地调用Step 1~5, 得到子树Ti, 返回Ti.
2梯度提升决策树算法
在梯度提升的每个阶段, 1≤m≤M, 假设存在一个不完美的模型Fm, 给它增加一个估计值h(x)得到一个更好的模型Fm+1(x)=Fm(x)+h(x) . 梯度提升算法认为一个好的h(x) 需要满足如下等式:
Fm+1=Fm(x)+h(x)=y,
或
h(x)=y-Fm(x).
(1)
因此, 梯度提升不断拟合余数式 (1), 每个Fm+1都试着去校正它的前一个Fm.
具体算法流程如下:
Step 2Form=1 toM:
② 训练时使用全部训练集,使一个基本的决策树学习算法拟合伪余数rim.
④ 更新模型Fm(x)=Fm-1(x)+γmhm(x).
Step 3 输出Fm(x) .
把决策树(例如C4.5) 作为梯度提升的基本学习算法就得到梯度提升决策树算法.
3C4.5-MI 和 GDBT-MI 算法
对于C4.5算法, 一颗决策树的长成是基于熵和相关准则启发式得到的. 假设有一个样本集D包含p个正样本和n个负样本, 对于这个二分类的D的熵定义为
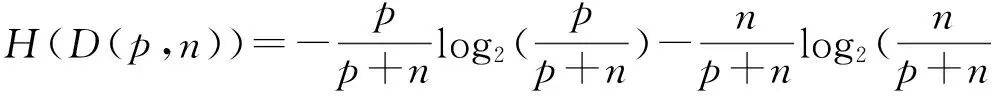
(2)

在 C4.5算法中用到了信息增益比, 即
gR(D(p,n),A)=g(D(p,n),A)/H(D(p,n)).
(3)
需要拓展式 (2)和式 (3)使其适应多示例框架. 首先引入两个函数α(D) 和β(D),给定一个多示例训练集合D,α(D) 和β(D) 返回的是集合D中的正负包( 样本) 个数. 考虑到一个样本是由多个示例构成的,必须重新定义刻画任意样本集合的纯度.
在多示例问题中,本文的目标是学习一个区分样本正负的模型, 而不是区分某一个样本中示例的正负. 因此, 这里的纯度不应该定义在示例个数p和n上, 而应该是定义在样本集合D中包含正负包的个数α(D)和β(D)上.
多示例的熵定义为

多示例的信息增益比定义为
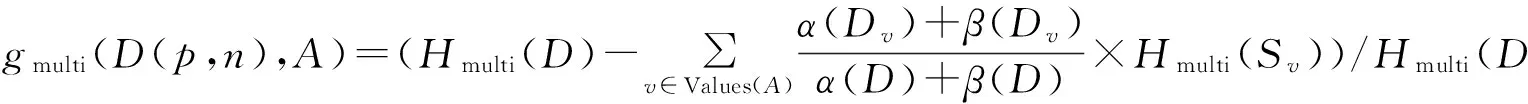
在一个决策树中直接显示多示例熵会得到异常复杂的树. 假如一个正包包含两个示例, 根节点的左子树代表第一个示例, 右子树代表第二个示例. 如果左子树成功地将第一个示例划分为正的示例, 那么这个包( 样本) 就可以判定为正包,因此推演右子树划分其他示例类型将毫无意义. 但是, 一个决策树模型 (如C4.5) 利用多示例熵将会倾向把所有的示例都划完为止, 这将会导致树变得复杂.
为了避免这个缺点,将推演过程修改如下:一旦一个正包中的示例被正确地划分为正的示例, 移除包中余下的示例.只要一个子树成功地为一个示例贴上正的包标签, 另外的一个示例就直接被移除. 基于多示例熵以及对以上树生成的修剪, 经典的决策树 C4.5就被拓展成多示例版本C4.5-MI.
为了得到更好的分类效果, 把 C4.5-MI 作为梯度提升方法的基本分类器就得到了GDBT-MI 算法.
4仿真实验

表1 MUSK 数据集的一些特性
用两个标准的多示例测试集 MUSK1 和 MUSK2 测试了C4.5-MI 和 GDBT-MI算法. MUSK数据集是用来模拟药品分子的, MUSK2比 MUSK1含有更多的可能构造.因此, MUSK2 比 MUSK1 更难准确分类. MUSK 数据集的一些特性在表 1 中列出. Elephant、Tiger和 Fox 为三个图像分类数据集.正包是包含某种动物的图片,负包是不包含该动物的图片. 这里的一个图片就代表一个包( 样本) , 包中含有图像的子区域( 多示例).一个图片是一个正包,则每个数据集包含100个正包和100个负包, 每个子区域看成表示为230 维向量的示例. 更多信息可见文献 [8].
为了获得较好的可比性,通过十折交叉验证比较了 MITI, ID3-MI, C4.5-MI, GDBT-MI 四种算法. 表2中MSUK 数据集的结果取自于文献[5—6], 其他的结果由作者根据文献[5—6]实现了MITI和ID3-MI算法,并测定了它们在Elephant、Fox和Tiger三个数据集上的精度. 这几种算法都是改进的决策树算法,测试结果见表2.可以看出,所提出的 C4.5-MI 算法要优于 ID3-MI算法, 比MITI算法稍逊. MITI算法采用较为复杂的启发式扩建子树, 内存开销和计算时间开销非常大, 而 C4.5-MI 算法构建子树较为简单明了, 计算量相对MITI 小很多,需要的内存空间也不大, 同时能够取得相对于ID3-MI算法不错的测试精度.

表2 4种算法在benchmark数据集的测试结果

图1 随着迭代次数的增加,GDBT-MI 算法的训练和测试误差Fig.1 The train and test error of GDBT-MI as the the number of iteration increasing
在通过梯度提升算法之后, GDBT-MI算法的分类精度处于最好的位置,在除 MUSK2 以外的数据集上测试误差都达到了最小.图 1 记录了GDBT-MI算法在MUSK1 和 MUSK2 数据集随着提升迭代次数的增加输出分类训练和测试精度的结果. 可以看出, 随着迭代次数增加, GDBT-MI 的训练和测试误差越来越低. 当迭代次数达到200 以上, 输出精度几乎不再变化. 对于 MUSK1数据集,在迭代次数达 150 次之后, 训练误差基本上接近零. 然而, 对于MUSK2数据集, 200 次迭代之后的训练误差为 0.06, 测试误差则降为0.121, 训练和测试误差均不如在 MUSK1数据集上的效果. 这可能是由于MUSK2数据集比MUSK1数据集的构造更为复杂. 因为梯度提升算法不易过拟合, 所以迭代次数越多, 效果会越好.
5小结
考虑到多示例学习的特殊性,提出了包层次上的信息熵和信息增益比,进而提出了一种基于 C4.5 的多示例学习算法;进一步采用梯度提升方法来优化基本的多示例决策树, 得到了性能更优的 GDBT-MI算法, 同时随着迭代次数增加, 能够进一步提升算法效果. 在将来的研究工作中, 如果在多示例决策树中加入一些正则化策略可能会使结果更好.
参考文献:
[1]DIETTERICH T G, LATHROP R H, LOZANO-PEREZ T. Solving the multiple-instance problem with axis-parallel rectangles[J]. Artificial intelligence, 1997,89(1/2):31—71.
[2]HONG R, WANG M, GAO Y, et al. Image annotation by multiple-instance learning with discriminative feature mapping and selection[J]. IEEE transactions on cybernetics, 2014, 44(5): 669—680.
[3]XIE Y, QU Y, LI C, et al. Online multiple instance gradient features selection for robust visual tracking[J]. Pattern recognition letters, 2012,33(9):1075—1082.
[4]ZEISL B, LEISTNER C, SAFFARI A, et al.On-line semi-supervised multiple-instance boosting[C]//IEEE Conference on Computer Vision and Pattern Recognition.San Francisco, 2010:1879—1894.
[5]CHEVALEYRE Y, ZUCKER J D. Solving multiple-instance and multiple-part learning problems with decision trees and rules sets:application to the mutagenesis problem[M]// Lecture Notes in Computer Science.Berlin: Springer, 2000:204—214.
[6]BLOCKEEL H, PAGE D, SRINIVASAN A. Multi-instance tree learning[C]// Proceedings of the 22nd International Conference on Machine Learning.Bonn, 2005:57—64.
[7]李航. 统计学习方法[M]. 北京: 清华大学出版社, 2012.
[8]ANDREWS S, TSOCHANTARIDIS I,HOFMANN T. Support vector machines for multiple-instance learning[M]// Advances in Neural Information Processing Systems .Cambridge: MIT Press,2002:561—568.
(责任编辑:孔薇)
A Multi-instance Learning Algorithm Based on Decision Tree
WANG Jie1,CAI Liangjian1,GAO Yu2
(1.SchoolofElectricalEngineering,ZhengzhouUniversity,Zhengzhou450001,China;2.SchoolofInformationEngineering,ZhengzhouUniversity,Zhengzhou450001,China)
Abstract:A new multi-instance learning algorithm C4.5-MI based on decision tree C4.5 was proposed, and the entropy function and information gain ratio to multiple instance framework were extended. Excellent algorithm GDBT-MI was obtained by improving C4.5-MI through adopting gradient boosting. The results on several benchmark datasets demonstrated the effectiveness of C4.5-MI and GDBT-MI over other similar algorithms.
Key words:multi-instance learning; decision tree; gradient boosting; C4.5 algorithm
收稿日期:2015-09-10
基金项目:教育部高等学校博士学科点科研项目(20124101120001); 河南省教育厅科学技术研究重点项目(14A41300); 中国博士后科学基金面上项目(2014T70685,2013M541992).
作者简介:王杰( 1959—) ,男,河南周口人,教授,博士生导师,主要从事模式识别与智能控制研究,E-mail: wj@ zzu.edu.cn.
中图分类号:TP181
文献标志码:A
文章编号:1671-6841(2016)01-0081-04
DOI:10.3969/j.issn.1671-6841.201507006
引用本文:王杰,蔡良健, 高瑜.一种基于决策树的多示例学习算法[J].郑州大学学报(理学版),2016,48(1):81—84.

