变利率相依风险模型破产概率的积分方程和界
吕海娟, 彭江艳, 武德安
(电子科技大学 数学科学学院 四川 成都 611731)
变利率相依风险模型破产概率的积分方程和界
吕海娟,彭江艳,武德安
(电子科技大学 数学科学学院四川 成都 611731)
摘要:考虑了一个带有随机利率离散时间相依风险模型,其中利率过程为独立同分布的随机变量序列,保费过程和索赔过程都具有高阶自回归结构.针对保费在期初收取和索赔在期末收取的情况,利用递归的方法,得出此模型破产概率的积分方程和上界、下界.
关键词:随机利率; 高阶自回归; 破产概率; 递归方法; 界
0引言
保险公司的破产概率是度量保险公司风险的最基本手段,风险模型的研究最开始是在连续时间的基础上进行的,但离散时间在实际保险风险中的应用性更强,如利率并不是连续变化的,是按阶段进行变化的,索赔也不会在事故一发生就进行.文献[1]对离散时间风险模型进行了讨论,之后不少学者对模型和结果进行拓展.文献[2]讨论了常利率下的相依风险情况,其中保费过程和索赔过程都仅限于一阶自回归结构(AR(1)).文献[3]研究了随机利率下离散时间保险风险模型,利用鞅技巧得出了最终破产概率的Lundberg界,其保费过程和索赔过程都仅是两个独立同分布的非负随机变量序列.文献[4]考虑了随机利率离散风险模型,得出了破产概率的递归方程和界,但其利率过程、保费过程和索赔过程都只是独立同分布的随机变量.文献[5]考虑保费收取和赔付为负二项过程、干扰为标准Wiener过程的多险种随机风险模型.文献[6—7]研究了常利率下风险模型.文献[8]研究了当利率服从AR(m)的离散时间风险模型,其保费过程和索赔过程依然是独立同分布的随机变量序列,得出了破产盈余分布.文献[9]讨论了理赔量具有一阶自回归的情形下,利用递归方法得出破产前的盈余分布.文献[10—11]研究了一类特殊的变利率离散时间风险模型,得到了破产前一刻盈余分布的一个上界估计.
本文在上述文献的基础上,在模型中引入更符合实际需求的随机利率,将保费过程和索赔过程推广到高阶自回归结构,引起证明过程难度化和构建技巧的复杂化.并且,高阶自回归结构在时间序列分析中比一阶自回归结构更具有普遍性,即在实际生活中,索赔额不仅仅与前一个阶段相关,可能与以往n个阶段相关.文中针对保费在期初收取和索赔在期末收取的情况,运用递归方法得出破产概率的积分方程和上界、下界.
1建立模型
考虑如下模型
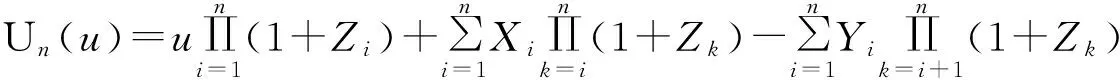
(1)
其中:
1)u为保险公司的初始准备金,u≥0,Un表示保险公司到n时刻的盈余.
2)Zi表示(i-1,i]时段内的利率,为独立同分布的非负随机变量列,G(z1)=P(Z1≤z1).
3)Xi表示(i-1,i]时段内的保费,服从高阶自回归AR(p)模型,即
Xn=a1Xn-1+a2Xn-2+…+apXn-p+δn,n=1,2,…,
(2)
其中:0≤ai<1;X1-i=x1-i≥0;i=1,…,p;x0,x-1,…,x1-p为保费以前p年的数据;δn为独立同分布的非负随机变量序列,H(x)=P(δ1≤x).
4)Yi表示(i-1,i]时段内的索赔额,服从高阶自回归AR(q)模型,即
Yn=b1Yn-1+b2Yn-2+…+bqYn-q+εn,n=1,2,…,
(3)
其中:0≤bi<1;Y1-i=y1-i≥0;i=1,…,q;y0,y-1,…,y1-q为索赔额以前q年的数据;εn为独立同分布的非负的随机变量序列,F(y)=P(ε1≤y)且F(0)=0.
5) 保费在时间区间初交纳,理赔在时间区间末进行.{Zn,n=1,2,…},{Xn,n=1,2,…},{Yn,n=1,2,…}相互独立.

φ(u,x0,x-1,…,x1-p,y0,y-1,…,y1-q)=P{T<}.
一般地,为保证保险公司平稳地运营,需假设纯利润条件E(Xn)>E(Yn),n=1,2,….
通过数学归纳法,可以得出(2)式等价于

(4)
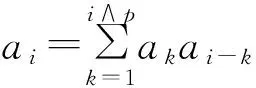
同理可得(3)式等价于

(5)

考虑到保险公司的运营,上述条件成立的前提条件是
E(δ)>E(ε),ai≥bi,x1-i≥y1-i;i=1,…,n,p∧q.
由等价性可得到如下纯利润条件

(6)
2破产概率的积分方程

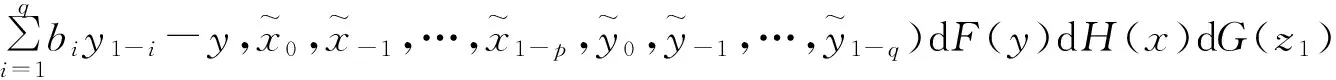
(7)

(8)
证明给定δ1=x,ε1=y,Z1=z1,
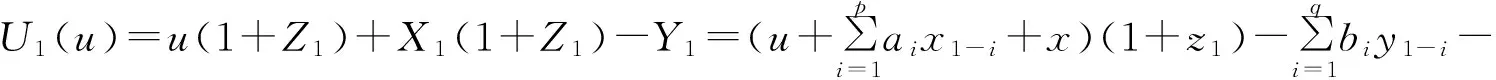

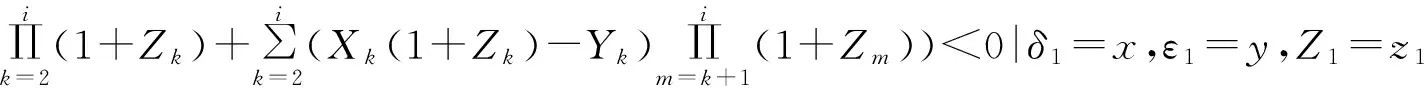
(9)
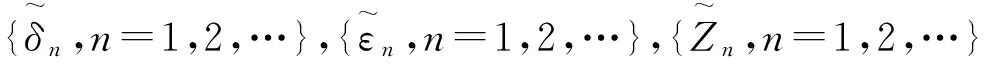

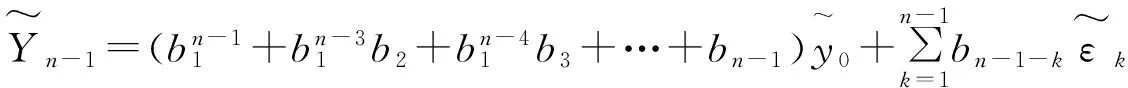
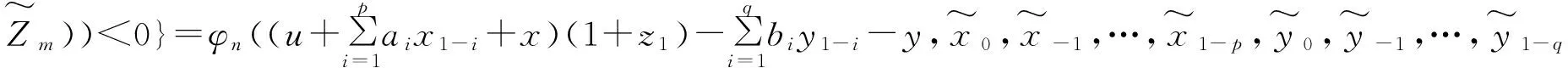
由全期望公式可得



3破产概率的界
为求破产概率的界,首先引入两个重要的量,其定义如下:

其中调节系数R>0满足
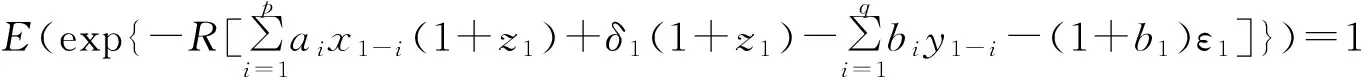
(10)

证明考虑如下函数的凸性

易知g″(s)≥0,所以g(s)是下凹函数.又因为g(0)=0,g′(0)<0,所以存在唯一的R>0满足(10)式,引理得证.
定理2在上述定理1的条件下,破产概率的界满足
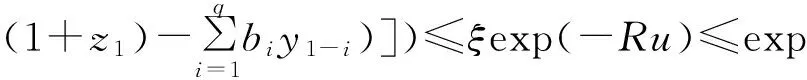
(11)
证明首先推导破产概率的下界.
由定理1中的积分方程可知

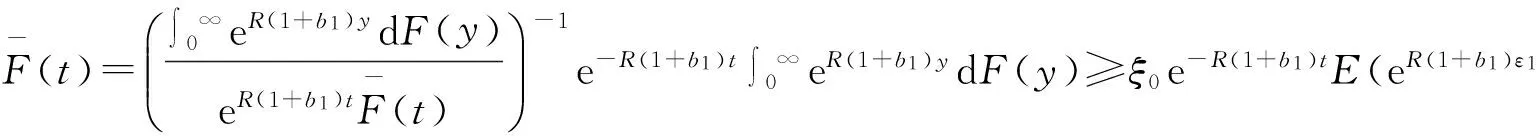


下界得证.下面利用数学归纳法求破产概率的上界.
对于∀t≥0有
ξe-Rt∫teR(1+b1)ydF(y)≤ξe-RtE(eR(1+b1)ε1),
(12)
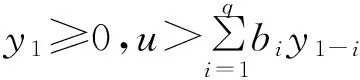
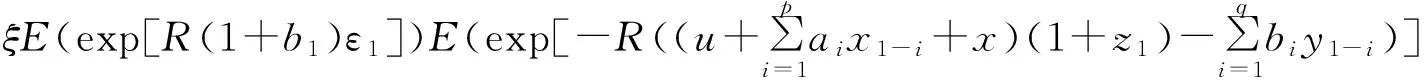
假设
φn(u,x0,x-1,…,x1-p,y0,y-1,…,y1-q)≤ξE(exp[R(1+b1)ε1])E(exp[-
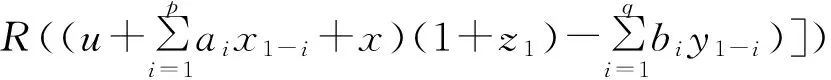


(13)
将(13)式和(12)式代入(7)式得
φn+1(u,x0,x-1,…,x1-p,y0,y-1,…,y1-q) ≤ξE(exp[R(1+b1)ε1])E(exp[-

(14)
因此,假设对于n=1,2,…都成立.对(14)式两边令n→取极限,由控制收敛定理得
φ(u,x0,x-1,…,x1-p,y0,y-1,…,y1-q)≤ξE(exp[R(1+b1)ε1])E(exp[-R((u+

由ξ<1和调节系数的定义可知φ(u,x0,x-1,…,x1-p,y0,y-1,…,y1-q)≤ξexp(-Ru)≤exp(-Ru).
综上,可得出破产概率的界(11)式.
参考文献:
[1]BOWERS N L,GERBER H U,HICKMAN J C,et al.Actuarial mathematics [M].Itasca Illinois:Society of Actuaries,1986.
[2]YANG H L,ZHANG L H.Martingale method for ruin probability in an autoregressive model with constant interest rate [J].Probability in the engineering and informational sciences,2003,17:183—198.
[3]王翠莲,刘晓.随机利率下离散时间保险风险模型[J].安徽师范大学学报(自然科学版),2007,30(1):19—20.
[4]WEI X,HU Y J.Ruin probabilities for discrete time risk models with stochastic rates of interest[J].Statistics and probability letter,2008,78(6):707—715.
[5]魏静,葛世刚,刘海生,等.带干扰的多险种复合负二项风险模型的破产概率[J].郑州大学学报(理学版),2015,47(2):33—36.
[6]PENG J Y,HUANG J.Ruin probability in a one-sided linear model with constant interest rate[J].Statistics and probability letters,2010,80(718):662—669.
[7]彭江艳.相依保险风险模型的理论研究[D].成都:电子科技大学,2011.
[8]于莉,詹晓琳,傅瀚洋.利率服从离散时间风险模型的破产分布[J].经济数学,2013, 30(4):90—93.
[9]于莉,詹晓琳,黄水弟.理赔量具有一阶自回归结构的离散时间风险模型的破产问题[J].上海第二工业大学学报,2014,31(1):61—66.
[10]余国胜.变利率离散时间风险模型破产问题[J].江汉大学学报(自然科学版),2014,42(1):32—35.
[11]夏征,王春伟,杨万才.一类带利率的马氏风险模型[J].河南科技大学学报(自然科学版),2011,32(6):72—76.
(责任编辑:方惠敏)
Integral Equations and Bounds for Ruin Probability in a Dependent Risk Model with Stochastic Interest
LYU Haijuan, PENG Jiangyan, WU De’an
(SchoolofMathematicalSciences,UniversityofElectronicScienceandTechnologyof
China,Chengdu611731,China)
Abstract:A discrete time dependent risk model was considered with stochastic interest where the interest rate process formed a sequence of independent and identically distributed random variables sequences, and both the premiums process and claims process had higher order autoregressive structures.The premiums were received at the beginning of each period and the claims were derived at the end of each period,integral equation upper and lower bound for infinite time ruin probabilities were derived by using recursive method.
Key words:stochastic interest rate; higher order autoregressive; ruin probability; recursive method; bounds
收稿日期:2015-07-08
基金项目:国家自然科学基金资助项目(71501025);中国博士后科学基金第57批面上项目(2015M572467).
作者简介:吕海娟(1989—),女,河北邯郸人,硕士研究生,主要从事概率统计及其应用研究,E-mail:1192435961@qq.com;通讯作者:彭江艳(1976—),女,四川成都人,副教授,博士,主要从事概率统计及其应用研究,E-mail:jiangeeryl@163.com.
中图分类号:O211.9
文献标志码:A
文章编号:1671-6841(2016)01-0045-06
DOI:10.3969/j.issn.1671-6841.201507014
引用本文:吕海娟,彭江艳,武德安.变利率相依风险模型破产概率的积分方程和界[J].郑州大学学报(理学版),2016,48(1):45—50.

