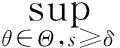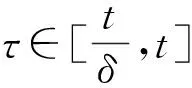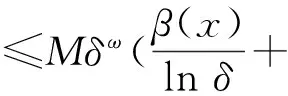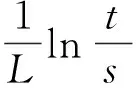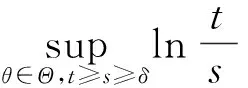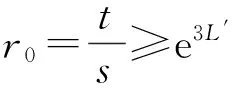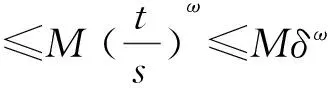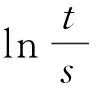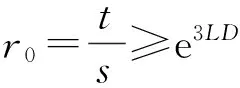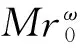巴拿赫空间中斜演化半流的多项式渐近行为
岳 田 , 刘开拓, 2, 雷国梁
(1.湖北汽车工业学院 理学院 湖北 十堰 442002;2.中南大学 数学与统计学院 湖南 长沙 410083)
巴拿赫空间中斜演化半流的多项式渐近行为
岳田1,刘开拓1, 2,雷国梁1
(1.湖北汽车工业学院 理学院湖北 十堰 442002;2.中南大学 数学与统计学院湖南 长沙 410083)
摘要:给出了斜演化半流一致多项式稳定和一致多项式不稳定的一些充要条件,用所得结论推广了已有结果.
关键词:斜演化半流; 一致多项式稳定性; 一致多项式不稳定性; 多项式增长
0引言
近年来,利用斜演化半流来研究无限维空间中演化方程的渐近性质取得了长足发展[1—3].关于斜演化半流的概念首先由Stoica和Megan[4]引入,与演化算子、演化族、斜积流不同的是它依赖于三个变量,而其他仅依赖于两个变量,因此利用斜演化半流来研究演化方程解的渐近行为更为合理,尤其是在指数稳定性方面.如文献[5]给出Banach空间中斜演化半流一致指数稳定的性质刻画,并得到了相应性质在一致集上的统一形式.文献[6]利用Banach函数空间及Banach序列空间分别给出了线性斜演化半流一致指数稳定的连续与离散特征.文献[7]给出了线性斜演化半流一致指数稳定的连续及离散型Barbashin 定理.文献[8]采用类似文献[5]中的方法,研究了斜演化半流非一致指数稳定的若干性质.在指数不稳定性方面,文献[4]对斜演化半流的一致指数不稳定性进行了研究,得到了相应的Datko型结论[9].文献[10]给出了斜演化半流的弱指数膨胀性相关性质,并利用Lyapunov函数来刻画了弱指数膨胀的相关特征.
由于指数渐近行为的要求比较苛刻,因此有必要寻找更为一般的关于斜演化半流的其他渐近行为.文献[11—13]针对演化算子提出了多项式稳定的概念,并给出了相应特征刻画.本文将在上述文献的基础上给出斜演化半流呈一致多项式稳定与不稳定的定义,并讨论相关性质,从而推广了Datko[9], Stoica及Megan[5]等人的结论.本文所用方法与文献[11]和文献[12]中方法不同,分别利用斜演化半流的收缩性及扩张性来研究其一致多项式稳定与不稳定特性.
1预备知识
定义1[5—7]σ:T×Θ→Θ为Θ上的演化半流,如果满足以下性质:
σ(t,t,θ)=θ, ∀(t,θ)∈R+×Θ;
σ(t,s,σ(s,r,θ))=σ(t,r,θ), ∀(t,s), (s,r)∈T, ∀θ∈Θ.
定义2[5—7]如果σ为Θ上的演化半流且映射Φ:T×Φ→L(X)满足如下条件:
Φ(t,t,θ)=I, ∀(t,θ)∈R+×Θ;
Φ(t,r,θ)=Φ(t,s,σ(s,r,θ))Φ(s,r,θ), ∀(t,s),(s,r)∈T, ∀θ∈Θ;
Φ(·,·,θ)x连续,∀(x,θ)∈ε.称π=(Φ,σ)为ε=X×Θ上的斜演化半流.
定义3如果存在常数M,ω,λ>0使得

(1)
斜演化半流π=(Φ,σ)称为是多项式增长的.
定义4若存在常数K,α,λ>0使得

(2)
斜演化半流π=(Φ,σ)称为一致多项式稳定的.
定义5如果存在常数K,α,λ>0使得

(3)
斜演化半流π=(Φ,σ)称为一致多项式不稳定的.
2主要结论
定理1 (收缩性)具有多项式增长的斜演化半流π=(Φ,σ)是一致多项式稳定的,当且仅当存在δ>0,r0>1,0 (4) 证明必要性显然,下面证明充分性. (5) 又因为 利用式(1)、(4) 及(5)可知 故斜演化半流π=(Φ,σ)是一致多项式稳定的. 定理2具有多项式增长的斜演化半流π=(Φ,σ)是一致多项式稳定的,当且仅当对∀x∈X,存在δ,β(x)>0使得 (6) 证明必要性显然,下面证明充分性. 设λ=δ,若t≤sδ,则有 (7) 进而由上式及式(5)可得 (8) 则由(6)式,对∀x∈X有 故再次利用一致有界原理可得,存在常数L′>0使得 定理3具有多项式增长的斜演化半流π=(Φ,σ)是一致多项式稳定的,当且仅当存在δ,D>0使得 (9) 证明必要性显然,下面证明充分性. 设t≥s,若s≤t≤sδ,则有 (10) (11) 定理4 (扩张性)具有多项式增长的斜演化半流π=(Φ,σ)是一致多项式不稳定的,当且仅当存在δ>0、r0、c>1使得对∀s≥δ,x∈X有 ‖Φ(r0s,s,θ)x‖≥c‖x‖. (12) 证明必要性显然,下面证明充分性. (13) 又因为 利用式(1)、式(12)可知 (14) 结合式(13)、(14)可得 故斜演化半流π=(Φ,σ)是一致多项式不稳定的. 定理5具有多项式增长的斜演化半流π=(Φ,σ)是一致多项式不稳定的,当且仅当Φ(t,s,θ)为单射,∀t≥s≥δ,θ∈Θ,且存在D>0使得 (15) 证明必要性显然,下面证明充分性. 任取t≥s≥δ.由多项式增长性知对∀τ∈[t,tδ]有 利用(15)式可得 参考文献: [1]YUE T, LEI G L, SONG X Q. Some characterizations for the uniform exponential expansiveness of linear skew-evolution semiflows[J]. Adv Math China, 2015, 44(7):1—10. [2]YUE T. Nonuniform polynomial dichotomy for noninvertible linear discrete-time systems in Banach spaces[J]. J Control Sci Eng, 2015, 2015:1—7. [3]HAI P H. A generalization for theorems of Datko and Barbashin type[J]. J Funct Spaces, 2015, 2015:1—5. [4]MEGAN M, STOICA, C. Exponential instability of skew-evolution semiflows in Banach spaces[J]. Stud Univ “Babes-Bolyai” Math, 2008, 53(1): 17—24. [5]STOICA C, MEGAN M. On uniform exponential stability for skew-evolution semiflows on Banach spaces[J]. Nolinear Anal, 2010, 72(3): 1305—1313. [6]HAI P H. Continuous and discrete characterizations for the uniform exponential stability of linear skew-evolution semiflows[J]. Nolinear Anal, 2010, 72(12): 4390—4396. [7]HAI P H. Discrete and continuous versions of Barbashin-type theorems of linear skew-evolution semiflows[J]. Appl Anal, 2011, 90(12): 1897—1907. [8]STOICA C, MEGAN M. On nonuniform exponential stability for skew-evolution semiflows in Banach spaces[J]. Carpathian J Math, 2013, 29(2): 259—266. [9]DATKO R. Uniform asymptotic stability of evolutionary processes in Banach spaces[J]. SIAM J Math Anal, 1972, 3(3): 428—445. [10] YUE T, SONG X Q, LI, D Q. On weak exponential expansiveness of skew-evolution semiflows in Banach spaces[J]. J Inequal Appl, 2014, 2014(1):1—11. [11]MEGAN M, CEUASU T, RAMNEANTU M L. Polynomial stability of evolution operators in Banach spaces[J]. Opuscula Math, 2011, 31(2): 279—288. [12]MEGAN M, CEUASU T, MINDA A A. On Barreira-Valls polynomial stability of evolution operators in Banach spaces[J].Electron J Qual Theory Differ Equ, 2011, 33: 1—10. [13]闫振海,刘再明,王帅鸽,等.一维非线性随机微分方程的随机指数稳定性[J].郑州大学学报(理学版),2015,47(2):20—23. (责任编辑:方惠敏) Polynomial Asymptotic Behaviors of Skew-evolution Semiflows in Banach Spaces YUE Tian1,LIU Kaituo1,2,LEI Guoliang1 (1.SchoolofScience,HubeiUniversityofAutomotiveTechnology,Shiyan,Hubei442002,China2.SchoolofMathematicsandStatistics,CentralSouthUniversity,Changsha,Hunan410083,China) Abstract:Some necessary and sufficient conditions for uniform polynomial stability and uniform polynomial instability were given, respectively. Generalizations of some well-known results were obtained due to Datko, Stoica, Megan in the case of polynomial asymptotic of skew-evolution semiflows in Banach spaces. Key words:skew-evolution semiflows; uniform polynomial stability; uniform polynomial instability; polynomial growth 收稿日期:2015-09-19 基金项目:湖北省自然科学基金资助项目(2014CFB629);湖北汽车工业学院校预研基金资助项目(2014XY06). 作者简介:岳田(1988—),男,四川南江人,助教,硕士,主要从事微分系统定性理论研究,E-mail: ytcumt@163.com. 中图分类号:O175.13 文献标志码:A 文章编号:1671-6841(2016)01-0041-04 DOI:10.3969/j.issn.1671-6841.201509021 引用本文:岳田,刘开拓,雷国梁.巴拿赫空间中斜演化半流的多项式渐近行为[J].郑州大学学报(理学版),2016,48(1):41—44.