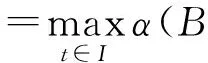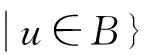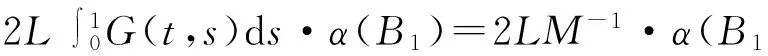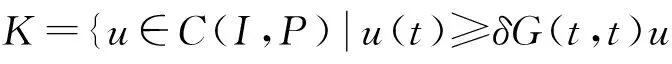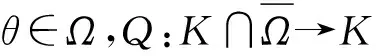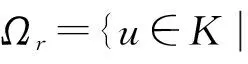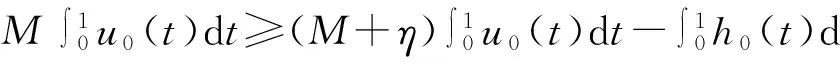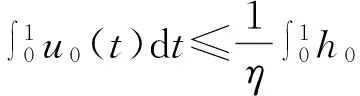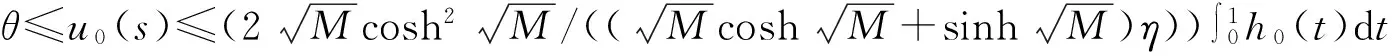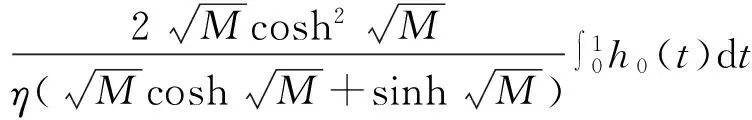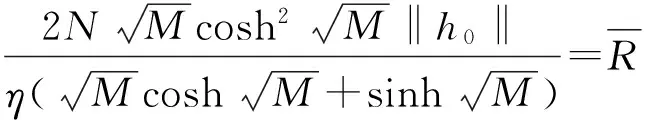有序Banach空间非线性Neumann边值问题正解的存在性
李小龙, 张 骞
(陇东学院 数学与统计学院 甘肃 庆阳 745000)
有序Banach空间非线性Neumann边值问题正解的存在性
李小龙,张骞
(陇东学院 数学与统计学院甘肃 庆阳 745000)
摘要:讨论了有序Banach空间E中的边值问题
-u″(t)+Mu(t)=f(t,u(t)),0≤t≤1,u′(0)=u′(1)=θ
的正解,其中f:[0,1]×P→P连续,P为E中的正元锥.通过新的非紧性测度的估计技巧与凝聚映射的不动点指数理论获得了该问题正解的存在性结果.
关键词:Neumann边值问题; 闭凸锥; 正解; 凝聚映射; 不动点指数
0引言
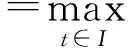

(1)
的正解,其中M>0为常数,f:I×P→P连续.
方程(1)的解和正解的存在性已有许多结论[1—6],主要利用不动点定理和单调迭代方法,但在一般的Banach空间中讨论的较少.本文在一般的Banach空间中,利用凝聚映射的不动点指数理论讨论了方程(1)正解的存在性.所得结果改进了文献[1—6]中的相关结论,并且是文献[7—8]在Banach空间中的推广,相应结果如文献[9].方程(1)的正解是指u∈C2(I,E)满足方程(1),并且u(t)>θ,0 (2) 由文献[2]知,(2)中G(t,s)为相应的Green函数,即 (3) (H0) 对∀R>0,f(I×PR)有界,且存在常数L=LR∈(0,M/4)使得对∀t∈I,D⊂PR,有α(f(t,D))≤Lα(D).其中PR={x∈P:‖x‖≤R}. 文献[1—3]中要求f在有界集上一致连续,而本文利用新的非紧性测度的计算与估计技巧[6]删去了这一要求,获得了方程(1)正解的存在性结果. 1预备知识及引理 在条件(H0)下,为了利用凝聚映射的不动点指数理论说明(2)式定义的算子Q:C(I,P)→C(I,P)为凝聚映射,需要以下非紧性测度的一些结果. 引理2[10]设B={un}⊂C(I,E)为可列集,若存在ψ∈L1(I)使得‖un(t)‖≤ψ(t),a.e,t∈I,n=1,2,…,则α(B(t))在I上可积,且α({∫Iun(t)dt})≤2∫Iα(B(t))dt. 引理3[6]设D⊂E有界,则存在D的可列子集D0,使得α(D)≤2α(D0). 引理4设f:I×P→P连续,假设(H0)成立,则Q:C(I,P)→C(I,P)为凝聚映射. 由(3)式易知,Green函数G(t,s)具有以下性质: (i) 0≤G(t,s)≤G(s,s),t,s∈I; (ii)G(t,s)≥δG(t,t)G(s,s),t,s∈I, (4) 引理5若f:I×P→P,则Q(C(I,P))⊂K. 证明对∀u∈C(I,P)及∀t,τ∈I,由(2)式和性质(i)有 又由(2)式和性质(ii)有 由(4)式,Qu∈K,即Q(C(I,P))⊂K. 因此当f:I×P→P时,Q:K→K为凝聚映射,方程(1)的正解即为Q在K中的不动点. 用引理6与引理7可以得到定理1. 2主要结果及证明 定理1设E为有序Banach空间,其正元锥P为正规锥,f:I×P→P连续,条件(H0)成立.假设f满足如下条件之一: (H1) ① 存在ε∈(0,M)及δ>0,使得当x∈Pδ时,f(t,x)≤(M-ε)x; ② 存在η>0及h0∈C(I,P),使得当x∈P时,f(t,x)≥(M+η)x-h0(t). (H2) ① 存在ε>0及δ>0,使得当x∈Pδ时,f(t,x)≥(M+ε)x; ② 存在η∈(0,M)及h0∈C(I,P),使得当x∈P时,f(t,x)≤(M-η)x+h0(t). 则方程(1)至少存在一个正解. 情形1在假设(H1)下,令0 u≠λQu,∀u∈K∩∂Ωr,0<λ≤1. (5) 反设(5)式不成立,则存在u0∈K∩∂Ωr及0<λ0≤1,使得u0=λ0Qu0.按Q的定义,u0满足微分方程 (6) 方程(6)在I上积分,并应用假设(H1)之①,有 另一方面,因为u0∈K,按锥K的定义,u0(t)≥δG(t,t)u0(s)≥θ,∀t,s∈I.于是 (7) 即u0(s)=θ于I,与u0∈K∩∂Ωr(‖u0‖=r)矛盾.于是(5)式成立,故由引理6知, i(Q,K∩Ωr,K)=1. (8) 取e∈P使得‖e‖=1,令v0(t)=e,则v0(t)是f(t,u(t))=Me时方程(1)的解,由Green函数的性质易知v0∈K{θ},下证当R充分大时,有 u-Qu≠τv0,∀u∈K∩∂ΩR,τ≥0. (9) 反设存在u0∈K∩∂ΩR及τ0≥0,使得u0-Qu0=τ0v0,则u0-τ0v0=Qu0,按Q的定义,u0满足微分方程 -u″0(t)+M(u0(t)-τ0v0(t))=-(Qu0)″(t)+MQu0(t)=f(t,u0(t)),t∈I. (10) 按假设(H1)之②,有 -u″0(t)+Mu0(t)=f(t,u0(t))+Mτ0v0(t)≥(M+η)u0(t)-h0(t),t∈I, 两边在I上积分得 由锥P的正规性,有 (11) 情形2在假设(H2)下,取0 u-Qu≠τv0,∀u∈K∩∂Ωr,τ≥0. (12) 其中v0(t)=e∈K,反设(12)式不成立,则存在u0∈K∩∂Ωr及τ0≥0,使得u0-Qu0=τ0v0,于是u0(t)满足微分方程(10).由(10)式及假设(H2)之①有 -u″0(t)+Mu0(t)=f(t,u0(t))+Mτ0v0(t)≥(M+ε)u0(t),t∈I. 在I上积分得 于是由(7)式可得u0(s)=θ于I,与u0∈∂Ωr矛盾.因此(12)式成立,故由引理7知 i(Q,K∩Ωr,K)=0. (13) 再证当R充分大时,有 u≠λQu,∀u∈K∩∂ΩR,0<λ≤1. (14) 假设存在u0∈K及0<λ0≤1,使得u0=λ0Qu0,则u0满足微分方程(6).将方程(6)在I上积分并应用假设(H2)之②得 (15) 参考文献: [1]郭大钧,孙经先.抽象空间常微分方程[M].济南:山东科学技术出版社,1989. [2]BERNFELD S, LAKSHMIKANTHAM V. Monotone methods for nonlinear boundary value problems in Banach spaces [J]. Nonlinear Anal,1979,3(3):303—316. [3]GUO D, LAKSHMIKANTHAM V. Multiple solutions of two-point boundary value problems of ordinary differential equations in Banach spaces[J]. J Math Anal Appl, 1988, 129(1):211—222. [4]周友明.Banach空间中二阶微分方程Neumann边值问题的解[J].应用数学,2004,17(3):479—485. [5]宋福民.Banach空间中两点边值问题的解[J].数学年刊:A辑,1993,14(6):692—697. [6]李永祥.抽象半线性发展方程初值问题解的存在性[J].数学学报,2005,48(6):1089—1094. [7]蒋达清,刘辉昭.二阶微分方程Neumann边值问题正解存在性[J].数学研究与评论,2000,20(3):360—364. [8]SUN J P, LI W T. Multiple positive solutions to second-order Neumann boundary value problems[J]. Appl Math Comput, 2003,146(2):187—194. [9]刘晓亚.Banach空间脉冲微分方程周期边值问题的正解[J].郑州大学学报(理学版),2012,44(1):15—19. [10]HEINZ H R. On the behaviour of measure of noncompactness with respect to differention and integration of vector-valued functions[J]. Nonlinear Anal,1983,7(12):1351—1371. [11]郭大钧.非线性泛函分析[M].济南:山东科学技术出版社,1985. [12]余庆余.半序Banach空间中的凝聚映射及其正不动点[J].兰州大学学报(自然科学版),1979,15(2):23—32. (责任编辑:孔薇) Existence of Positive Solutions for Nonlinear Neumann Boundary Value Problems in Ordered Banach Spaces LI Xiaolong,ZHANG Qian (CollegeofMathematicsandStatistics,LongdongUniversity,Qingyang745000,China) Abstract:The existence of positive solutions for value problem -u″(t)+Mu(t)=f(t,u(t)), 0≤t≤1,u′(0)=u′(1)=θ in an ordered Banach spacesEwas discussed,wheref:[0, 1]×P→Pwas continuous, andPwas the cone of positive elements inE. An existence result of positive solutions was obtained by employing a new estimate of noncompactness measure and the fixed point index theory of condensing mapping. Key words:Neumann boundary value problem; closed convex cone; positive solution; condensing mapping; fixed point index 收稿日期:2015-08-21 基金项目:国家自然科学基金资助项目(11561038);甘肃省高等学校科研项目(2015A-149). 作者简介:李小龙(1976—),男,甘肃甘谷人,副教授,硕士,主要从事抽象发展方程及其应用研究,E-mail:lixl80@163.com. 中图分类号:O175.15 文献标志码:A 文章编号:1671-6841(2016)01-0023-04 DOI:10.3969/j.issn.1671-6841.201503006 引用本文:李小龙,张骞.有序Banach空间非线性Neumann边值问题正解的存在性[J].郑州大学学报(理学版),2016,48(1):23—26.