基于模糊聚类法的油气集输系统优化设计
许晓明,李 华,杨 超,李彦兰中国石油勘探开发研究院,北京 100083
基于模糊聚类法的油气集输系统优化设计
许晓明,李华,杨超,李彦兰
中国石油勘探开发研究院,北京100083
摘要:油气集输系统优化设计对地面建设成本控制和保证油田高效生产起着重要作用。以油气集输管网系统投资极小化为目标,综合考虑多级星式管网拓扑结构特点、生产运行参数等多种影响因素,建立了多级星式油气集输系统模糊优化数学模型;并采用模糊c-均值聚类方法对该模型进行优化,得到最优中转站个数、最佳中转站位置、最优网络级数等。通过实例分析与结果对比表明,模糊c-均值法计算结果可靠,能够解决传统优化设计方法中效率与效果不能兼顾的矛盾,有助于油田地面“管-站”部署及优化调整设计,实用性较强。
关键词:油气集输系统;多级星式拓扑结构;模糊聚类;模糊优化
油气集输系统主要是将来自各采油井的采出液通过集输管道运输到指定的集输站,最终输送到油库。其投资费用十分巨大,不仅对油田地面成本控制起着决定性的作用,同时对保证油田正常生产也起着重要作用。多级星式油气集输管网形式是一种普遍应用于油田实际生产的集输管网部署规划方式,其特点是在采油井的位置和井数给定的情况下,优化出最佳中转站个数及位置并进行星式网络连接。多级星式集输管网系统的优化是一类涉及离散拓扑优化、非线性参数优化等的大型混合优化问题[1- 4]。目前解决多级星式油气集输系统优化的方法主要是直接搜索法、贪心法、0- 1规划法、拉格朗日松弛法、混合遗传算法[5]、神经网络法[6]、蚁群算法[7],这些方法仅部分适用于某些特定较简单管网系统[8],而混合遗传算法和神经网络法虽然能整体考虑油田地面管网优化系统,但计算耗时较长,很大程度上影响了工作效率。基于模糊聚类法的油气集输系统优化设计建立在拓扑优化模型的基础之上,利用模糊数学理论结合多级星式网络形态,既考虑油田经济效益及管道强度、稳定性等因素,又能快速优化油田地面管网的部署,达到极小化投资与高效快速优化相结合的目的。
1 油气集输系统拓扑优化数学模型
油气集输管网的优化是在已知各油井位置等因素的基础上,为满足生产要求进行的管网布局的优化设计。该优化设计系统主要包括:管网集输级数、各级别集输管网的连接方式、中转站个数、中转站位置等参数的优化。
油气集输管网建设的优劣,主要评判标准就是在保证油气集输正常运转的情况下,建设成本投入的大小,因此油气集输系统优化设计的目标函数采用在满足油田正常生产要求的前提下极小化整个管网系统的建设投资费用。
油气田集输系统优化问题的数学模型可表示为:

s.t.集输管网拓扑结构约束
式中:U为系统变量,包括各管网系统的布站级数、各个站的处理规模等;E为整个管网系统的连接关系,包括油井-中转站、中转站-集输站的连接关系等;S为系统中各个站的几何位置向量,如中转站或集输站的位置;F(U,E,S)为系统建设投资,包括中转站、计量站等站的投资和管道投资。
集输管网拓扑结构对整个管网系统优化起到至关重要的作用。目前国内广泛采用的油气集输管网拓扑结构是多级星式集输管网形式[10- 11],其拓扑形式是:网络由多级管理功能所决定,各顶点分别归属于不同级别点的集合中,低级顶点受到高级顶点的管理,且这种隶属关系具有唯一性,如图1所示。多级星式网络拓扑结构的特点是,遇到障碍物等情况时,改变网络布局中的一部分不会影响整体的拓扑结构。
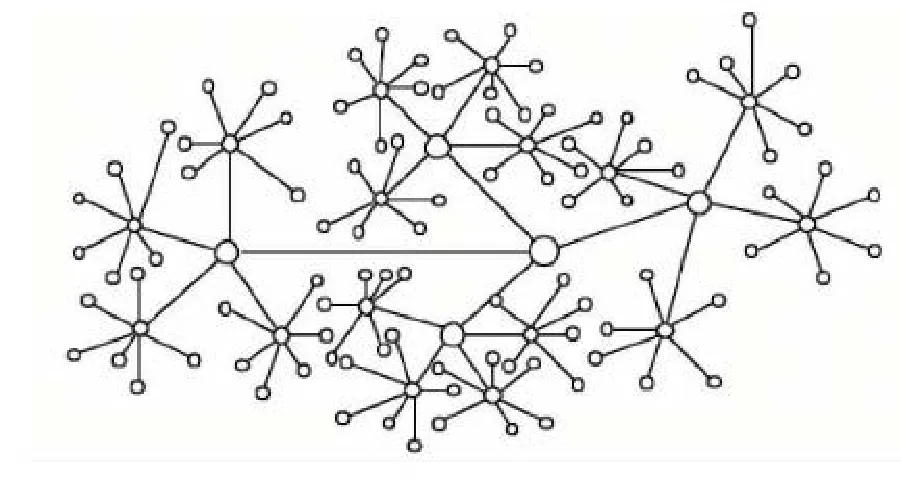
图1 多级星式网络拓扑示意
本文结合油气集输系统优化设计目标函数及多级星式网络拓扑布局的特点,建立了如下多级星式油气集输系统优化设计数学模型:


式中:dijk为与之间的距离函数;fij为点的自身造价;N为星式网络的级数;S0为星式网络中最低级别点的集合;Si为第i级别点的集合,i =1,2,…,N;Vi为Si中各点几何位置向量;mi为Si的维数。
2 油气集输系统模糊拓扑优化
2.1模糊c-均值聚类
基于目标函数的聚类算法中模糊c-均值(FCM,Fuzzy c- Means)类型算法[12- 13]的理论最为完备、应用范围最广。模糊c-均值类型的算法是从硬聚类目标函数的优化中导出的,为了借助目标函数法求解聚类问题,利用均方逼近理论构造了带约束的非线性规划函数,给出交替优化算法,最终得出最优聚类结果。
首先对给定样本集S的聚类分析就要产生S的c划分,数据集S ={s1,s2,…,sn}⊂Rs为模式空间中n个模式的一组有限观测样本集,Sk={sk1,sk2,…,sks}⊂Rs为观测样本sk的特征矢量,对应特征空间中的一个点,skj为特征矢量sk的第j维特征的数值。
数据集S的c划分得到的c个子集S1,S2,…,Sc如果满足式(11)的条件,则称之为S的硬c划分:

用隶属度函数μik表示样本sk与子集Si(1≤i≤c)的隶属关系,则模糊c-均值划分中μik为子集Si(1≤i≤c)的特征函数,显然有μik∈[0,1],这样S的硬c划分也可以用隶属函数表示,即用c个子集的特征函数值构成的矩阵U =[μik]c×n来表示。矩阵U中的第i行为第k个子集的特征函数,而矩阵U中第k列为样本Sk相对于c个子集的隶属函数。于是S的硬c划分空间为:
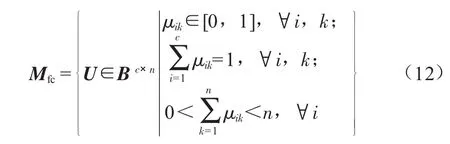
式中:Bc×n为c行n列的模糊矩阵。
为了在可能的这些分类中寻求合理的分类结果,取带约束的非线性规划函数为聚类准则。假设U =[μik]c×n为硬划分矩阵,pi(i =1,2,…,c)表示第i类的典型矢量或聚类原型矢量,pi=(pi1,pi2,…,pis)∈Rs。则

式中:F(U,p)表示聚类准则,为带约束的非线性规划函数。
2.2运用模糊- c均值聚类解拓扑优化数学模型
在油气集输系统中,首先进行的是管网拓扑优化,确定中间站的个数、井网集合及管网的连接关系。首先应用模糊c-均值聚类法对各个油井进行聚类,然后找出各个聚类中心即一级中间站的个数及位置,然后确定中间站与各油井的连接关系,接着确定二级中间站的个数及位置,然后确定一级中间站与二级中间站的连接关系,直至达到理想的星式网络级数。
应用模糊c-均值法对星式网络拓扑形式进行优化,首先将集合Si作为第i个级别的数据集,其中Ui为观测样本的特征矢量,对给定样本集的聚类分析要产生Si的Ci划分。且满足式(11),用隶属度函数μijk表示样本Sij与子集Ukij的隶属关系,则模糊c-均值划分中μijk为子集Ukij的特征函数,显然有μijk∈[0,1],且

为了得出最优多级星式油气集输系统的拓扑布局,则:
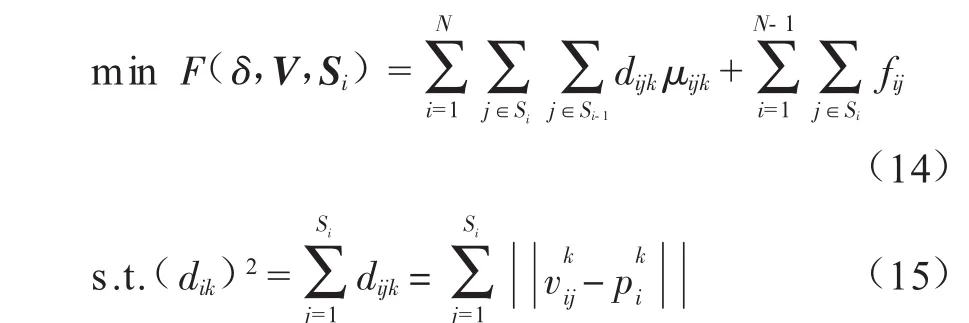

式中:pi(i =1,2,…,mi)表示第i类的典型矢量或聚类原型矢量;Vi=(vi1,vi2,…,vimi)表示Si中各点几何位置向量。
应用拉格朗日乘数求解得:
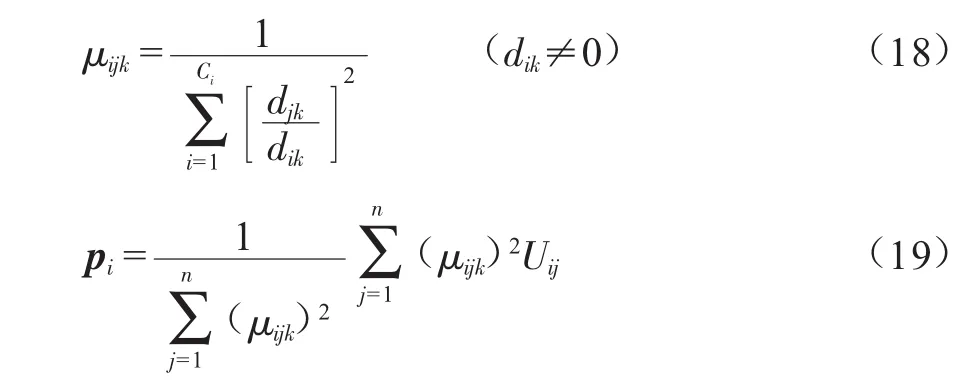
由此得到第i个级别数据集Si的Ci划分,聚类中心为pi。
2.3确定第i个级别数据集的最优分类个数
由上述得出第i个级别数据集Si的Ci划分及聚类中心pi,为了使所得到的拓扑优化模型在满足生产要求的前提下极小化整个管网系统的基础建设投资和生产运行费用,本文进一步确定每个级别点的最优分类个数Ci。
(1)给定初始油井几何位置向量Ui={ui1,ui2,…,Uimi}作为数据集。
(2)附初值Ci= 1,代入式(14)~(19)得到i级中转站的向量坐标pi及μijk,并代入式(3)式,记此时的目标函数F(δ,V,M)= f。
(3)令Ci+ 1⇒Ci,回到第(2)步,若F(δ,V,M)<f,令f等于新的F(δ,V,M),记下此时的pi及μijk,直到Ci+1等于mi(mi为第i级别数据集Si的维数)。
由此迭代循环得出第i个级别的最优中转站个数(即最优分类个数)及中转站的位置坐标(即聚类中心坐标)。
2.4多级星式油气集输系统的拓扑优化
经上述模糊c-均值聚类算法的迭代得出了每个级别的中转站个数(即Ci)以及中转站的坐标向量(即聚类中心pi),将每一聚类集中的点与聚类中心进行星式连接,即δijk=1的点连接,完成每一级别的星式拓扑网络,直至达到预定的最优网络拓扑布局。星式网络拓扑优化布局的计算框图见图2[14]。
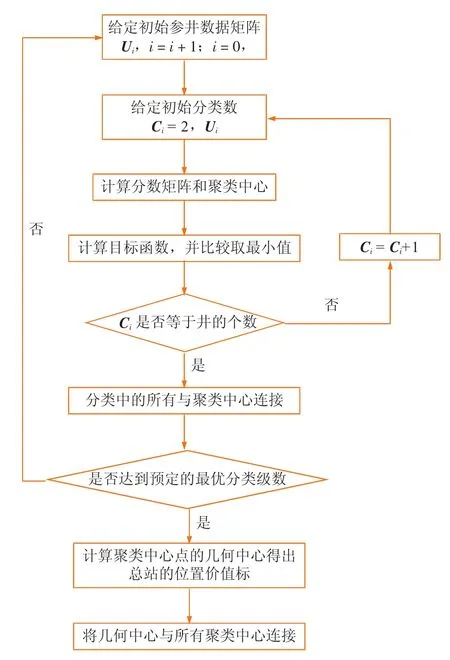
图2 星式网络拓扑优化计算流程
3 应用实例
基于上述理论研制了软件系统,并以东部某油田区块的实际井位数据为例,应用该软件对该区块的油气集输系统进行了优化设计,同时与传统的分级优化法进行了对比。
3.1模糊- c均值优化二级星式油气集输系统
该区块地面井数为180口,经过软件数字化后得出了油田的井位图(见图3),根据这180口井的实际情况,设计二级星式网络拓扑布局,通过式(2)~(10)建立二级星式油气集输系统优化设计的数学模型。
根据模糊c-均值法求解得出目标函数达到最小值时,最优分类个数为8,此时系统建设成本为最小。图4为分类个数与目标函数值的关系。
由得出的最优分类及分类中心位置,按照星式拓扑布局结构进行了一级网络的星式网络连接,如图5所示,每个井点与分类中心进行了星式连接。在第2级别数据集中,经过计算得出最优分类个数为1个,每个中转站与最终联合站的连接为星式连接。

图3 油田井位

图4 分类个数与目标函数值关系

图5 二级星式网络
3.2与传统分级优化比较
分级优化法是解决复杂问题的有效途径。对于一般油田地面管网的优化设计问题,分级优化主要是采用两级优化法进行星式网络的优化设计:拓扑级优化和几何级优化,这两级优化之间通过迭代来协调。分级优化后得出的优化结果为:第一级别管站系统建立最优中间站个数为14个,第二级别建立1个联合站,拓扑布局形式如图6所示。
通过程序计算结果可以得出,分级优化的管道费用和建中间站联合站的费用一共为3 842万元,模糊聚类分析优化算法的费用为3 768万元。因此模糊聚类法应用于油田实际井网分布拓扑图能达到较好的效果,同时模糊聚类法进行优化计算耗时更少。
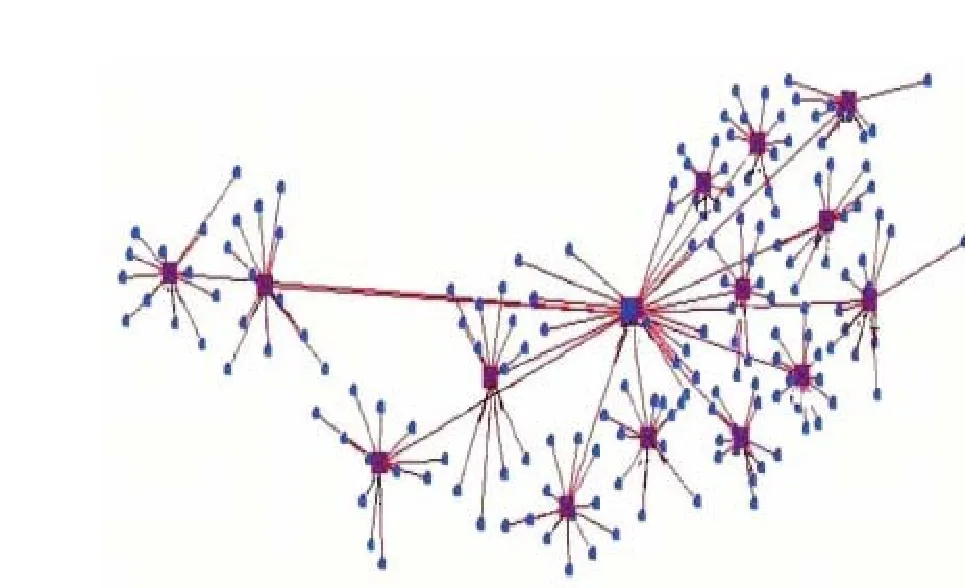
图6 分级优化星式网络
4 结论
针对油气集输系统的优化设计问题,以极小化系统建设成本为目标,综合考虑多级星式管网拓扑结构特点、生产运行参数等多种影响因素,建立了多级星式油气集输系统优化数学模型。
本文以模糊数学为基础,首次应用模糊c-均值聚类方法对油田地面管网系统进行优化,确定了管网的最佳中转站个数、位置以及管网最优拓扑布局。本方法理论性较强,通过与传统分级优化算法进行比较,其优化效果更好、计算速度更快,有助于指导油田管网部署及优化调整,实用性较强。
参考文献
[1]孙晓群,田甜,朱秀姣.提高中原油田油气集输系统效率的有效做法[J].石油工程建设,2009,35(4):63- 65.
[2]刘万丰.油气集输系统生产运行方案优化方法[J].油气田地面工程,2010(2):47- 49.
[3]王晓瑜.浅谈油气集输管网的优化设计[J].油气田地面工程,2004(7):44- 45.
[4]李元鹏,简朝明,宋江卫,等.油田地面集输管网优化计算研究[J].油气储运,2004,23(10):17- 19.
[5]韩仁涛,蒋建勋,王永清,等.油田地面注水管网布局优化中的遗传算法[J].断块油气田,2005,12(5):51- 52.
[6]魏立新,刘扬.油气集输系统障碍拓扑布局优化设计方法[J].石油学报,2006,27(6):120- 124.
[7]王洪元,卜莹,潘操.基于遗传蚁群算法的气田集输管网优化方法[J].计算机与应用化学,2012,29(12):1 495- 1 498.
[8]李勇,宁永乔,王薛辉,等.西南油气田地面工程关键技术综述[J].石油规划设计,2013(1):1- 7.
[9]刘扬,鞠志忠,鲍云波.一类多级星式网络的拓扑优化设计方法[J].大庆石油学院学报,2009(2):25- 29.
[10]杨建军,战红,刘扬,等.星状原油集输管网拓扑优化的混合遗传算法[J].西南石油大学学报(自然科学版),2008,30(4):166- 169.
[11]ALEX RODRIGUEZ,M TOMAS,JAIME Rubio- Martinez. A Benchmark Calculation for the Fuzzy C- means Clustering Algorithm:Initial Memberships[J]. Journal of Mathematical Chemistry,2012,50(10):2 703- 2 715.
[12]ZOU Kaiqi,WANG Zhiping,HU Ming. An New Initialization Method for Fuzzy C- means Algorithm[J]. Fuzzy Optimization and Decision Making,2008,7(4):409- 416.
[13]CORSINI P,LAZZERINI B,MARCELLONI F. A New Fuzzy Relational Clustering Algorithm Based on the Fuzzy C- means Algorithm[J]. Soft Computing,2005,9(6):881- 900.
[14]赵洪激,刘扬.油气集输系统优化设计软件[J].天然气与石油,2000,18(1):10- 14.

图片报道:某油田管站设施
Optimization Design of Oil/Gas Gathering and Transportation System Based on the Fuzzy Clustering Method
XU Xiaoming,LIHua,YANG Chao,LIYanlan
PetroChina Research Institute of Petroleum Exploration &Development,Beijing 100083,China
Abstract:The optimization of oil/gas gathering and transportation system plays an important role in the surface engineering cost controland oilfield production. The mathematicalmodelof fuzzy optimization of multilevel star network oil/gas gathering and transportation system is established,which takes many influence factors into account,such as the multilevel star network topology characteristics and operation parameters,and sets the system investment minimization as the optimization objective,then applies the fuzzy c- means clustering method to solve,and gets the results such as number of transfer stations,optimal transfer station locations and optimal network levels of pipeline stations. The analyses on living examples show that the calculation results of the fuzzy c- means clustering method are reliable and can resolve the contradiction of both considering efficiency and effectiveness in traditional optimization design method. It is helpful to“pipeline -station”arrangement and optimal adjustment design of oilfield surface construction,and has higher practicability.
Keywords:oil/gas gathering and transportation system;multilevel star topological structure;fuzzy clustering;fuzzy optimization
doi:10.3969/j.issn.1001- 2206.2016.02.002
基金项目:
国家科技重大专项(2011ZX05010- 002)资助。
作者简介:
许晓明(1984-),女,辽宁北票人,工程师,2010年毕业于中国石油大学(北京),主要从事高含水老油田油气开发工作。
Email:xiaomingxu@petrochina.com.cn
收稿日期:2015- 08- 10;修回日期:2015- 11- 31

