“冰桶挑战”诱导的社交网络演化分析
杨 凯,刘晓露,林坚洪,成 曦,郭 强,刘建国
(上海理工大学复杂系统科学研究中心,上海 200093)
“冰桶挑战”诱导的社交网络演化分析
杨凯,刘晓露,林坚洪,成曦,郭强,刘建国
(上海理工大学复杂系统科学研究中心,上海 200093)
摘要:考虑社交网络初始阶段的演化过程对于定量认识和理解人际关系的形成与演化的重要意义,搜集“冰桶挑战”事件国内从事件发起到第6天的数据。以挑战者为节点,点名关系为边构造社交网络。通过分析该网络的统计指标,发现网络密度一直减小;网络效率先减小,后又缓慢增加;连通子图的数量先迅速增加,最高增加了初始值的5倍,后又减小;网络效率与子图数量呈负相关关系。考虑到该网络构建的特殊性,与其他社交网络的演化做了对比分析。
关键词:社交网络;网络演化;拓扑结构;冰桶挑战
0引言
社会网络是描述社会关系的工具之一[1]。社交网络诞生初期的发展和演化对于理解人际关系的演化至关重要。2001年秋,哥伦比亚大学社会系的Watts等[2]建立了一个小世界项目的网站,开始在世界范围内进行一个检验六度分离假说是否正确的网上在线实验,该实验的目的是为了验证几十亿人口的整个世界是否有小世界现象。在一年多的时间里,总共有13个国家的18名目标对象和166个国家和地区的6万多名志愿者参与实验,最后有384个志愿者的电子邮件抵达了目的地。每封邮件平均转发5到7次即可到达目标对象。在Web2.0应用模式下[3],网络人际关系可通过新的方式重新构建。社交网络服务(social networking services,SNS)和微博(如新浪微博、Twitter)是最新出现的两种Web2.0应用模式,都属于在线社交网络[4]。针对社交网络的演化[5],很多学者基于理论模型做了分析,复杂网络中两个较早且比较著名的模型是小世界模型[6-7]和无标度模型[8]。张立等[9]在虚拟的社区网络上做了演化分析,并研究其拓扑结构。发现虚拟社区网络在演化过程中,节点的加入、边的加入、网络中度分布、节点的度与其加入网络时间的关系、平均度随时间的变化等方面与传统的无标度网络有所不符。熊熙等[10]考虑社交网络的聚类及连接随机性提出了一种混合演化模型。数值仿真表明该网络模型与实际社交网络数据的统计结果基本吻合。Ravi Kumar等[11]实证分析了大型在线社会网络结构的演化,并提出了一种能识别组元结构的网络增长模型,但他们仅仅截取了网络中间的部分数据,并没有从网络诞生时开始分析。信息及舆论在社交网络上的传播过程[12]也可以看作是一个网络演化的过程,当信息传播到一个用户时,那么该用户加入了这个信息网络。当前对于社会网络演化的研究无论从模型还是实证角度都是基于全网络的演化,并非局部关系的演化。
本文搜集了国内“冰桶挑战”事件从发起到发展到第6天的数据,以天为单位将数据划分,构造了不同时间上的网络。按照该活动的规则,该社交网络具有其特殊性——选择自己的亲密好友所构建的网络,可认为网络中边的关系为强关系。该网络相当于一般社交网络的一个“骨架”,是非常重要的结构。本文首先给出了该网络每天的演化过程,分析了该网络的密度、聚类系数及网络效率等结构特性,发现网络密度从开始的0.120 9逐渐下降,与Yahoo!360网络的密度演化有明显区别。聚类系数从初始值零增加到0.016 7后又缓慢减小,而整体聚类系数相对较小;网络效率先减小,从0.214 3降到最小值0.039 9,后又缓慢增加。聚类系数与网络效率这两个方面与Facebook网络上的演化也有异同,本文分析了其中的原因,而对比分析可以体现出本文网络的特殊性。最后,分析了网络的最大连通子图,连通子图的数量先迅速增加最高增加了初始值的5倍,后又减小。发现连通子图的数量与网络效率成负相关关系。本文的研究可以为构建相应的理论模型提供一定依据。
1数据描述与网络构建
1.1数据描述
“冰桶挑战”全称为“ALS冰桶挑战赛”,要求参与者在网络上发布自己被冰水浇遍全身的视频内容,然后该参与者便可以要求其他人(规则为3个人)来参与这一活动。活动规定,被邀请者要么在24小时内接受挑战,要么选择为对抗“肌肉萎缩性侧索硬化症”捐出100美元。而事件发展到后来活动者不仅接受挑战并且也捐出善款。2014年8月中旬,冰桶挑战赛活动蔓延至中国,多名科技界、演艺界及体育界名人被点名参与了这一活动。如率先完成挑战的一加手机创始人刘作虎,同时点名奇虎360 CEO周鸿祎、锤子科技CEO罗永浩、华为荣耀业务部总裁刘江峰参与该挑战。基于这一活动规则,由发起挑战者点名接力,然后这样传下去,这样就形成了一个社交网络。
本文主要基于新浪微博这一社交网站,搜集了2014年8月17日00:00点—8月22日24:00,6天的冰桶挑战者的数据,挑战者都会将视频上传到微博及相关社交网站,并在网站中点名其他人参与。基于此,搜集了参与挑战者的相关信息包括自愿挑战者(即没被别人点名,自愿加入该活动的人)——自动加入网络的节点,他们接受挑战的时间(上传视频的时间)以及他点名的挑战者,接下来被点名的人接受挑战的时间及他点名的人。共搜集了6天786名挑战者及他们的挑战关系的数据。
1.2网络构建
本文以天为划分单位,分别构建了17日—22日6天的“冰桶挑战”网络。每个挑战者作为网络中的一个节点,点名关系用网络连边表示。为了便于观察每天参与者的变化情况,本文把将挑战者的关系统一编号,赋予不同的灰度,如图1所示,不同灰度表示不同时间(以天为划分单位)的网络节点(由内到外时间依次增加)。从图1可以发现随着时间变化,挑战者数量不断增加,相应的网络不断扩大。接下来分析具体网络结构的演化的过程。
2网络的演化特性
首先分析网络每天的结构及其演化过程,图2展示了该网络的演化过程。
从图2可以直观看出该网络的演化过程中的一些特点:开始时节点较少,即事件发生初期参与挑战的人较少,接着有节点缓慢增加的过程,而后受到社交媒体的影响,参与者越来越多,网络节点急剧增加到后面网络演化已不可控制。该过程类似于在线社会网络上的信息传播,信息如果按照既定规则来,就会以某一节点为中心散发。然而从图中观察发现,在第1天有“刘作虎”、“古永锵”和“叶丙成”3人加入网络,并且“叶丙成”只点了两个人并没有遵循既定规则,所以网络的演化并不会像既定规则那样发展。网络形成时的状态对于以后的网络演化有重要的影响,到了第2天自动加入网络的节点变得更多,这些节点增加也没有一定的规则,是随机加入到网络的,因此网络呈现不规律的增长。在实际社交网络中,有些参与者会破坏既定规则——有的自动加入到网络,有的点名不是3人,导致网络的演化没有一定的规律,这也是现实社交网络难以用现有理论模型拟合的主要原因。
2.1理论模型
根据“冰桶挑战”网络的演化规则,本文建立一个简单的理论模型与实际情况对比分析,理论模型如下:
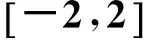
2.2网络规模
网络规模的变化体现整个网络的演化特征,本文从网络的节点数、边数及每个网络新增节点数的角度与理论模型对比分析,如图3所示。
由图3a与b可以看出网络规模不断扩大,开始时节点增加缓慢,接着急剧增加,到第5天第6天节点增加缓慢。同样,网络中边的数量也不断增加,开始时由于参加者较少,边数增加缓慢,到第3第4第5天时由于节点数显著增加,边数也急速增加,而最后一天增加变缓。对比分析,理论模型有些不同:在开始阶段网络中节点数和边数增加缓慢,到第5天第6天时增加迅速,与实际情况差别较大。因为实际社交网络的演化受一些人的主观因素及外界客观因素的影响,理论模型并没有考虑这些因素。接下来,分析网络每天新增加节点数的变化。
从图3c可知,在网络形成初期网络每天实际新增加节点数从14到48到141再到224迅速增加,相比理论模型的指数式增长快。分析原因:一方面由于很多人打破了既定规则,另一方面由于社交媒体的显著影响使得人们得到纷纷响应。这也说明在该网络生成与演化过程中,由于受其他因素的影响,现有的理论模型并不适用于类似社交网络的演化。而第5第6天网络的新增节点数由226变为了133,增加变缓并且有所下降,说明这一事件过了一定的热度,相应地参与者变少;另一方面观察数据发现在第5天和第6天加入的用户,在社交网络上一般为普通用户,粉丝量较少不会被社交媒体关注,大都不会在社交网络上发布相关信息,因此该网络就会在这些节点停止演化。
2.3网络的拓扑结构演化分析
分析了网络规模的变化,接下来具体分析网络结构特性是如何演化的。由于“冰桶挑战”规则所限,大家大都会点名自己的亲密朋友(强关系)参加挑战,体现在网络中边的方向只表示先后点名关系。在实际社交中他们互为朋友关系,体现在网络中即为双向关系。因此本文在计算网络指标时将该网络看成无向网络。
2.3.1网络密度
一个包含N个节点的网络的密度ρ定义为网络中实际存在的边数M与最大可能的边数之比。因此,对于无向网络有从图4a可以看出,该网络密度逐渐变小。网络节点的增加,虽然网络中边也增加,但两者不是同比例变化的,对于整个网络来说逐渐变得稀疏。
(1)
图4b为文献[11]研究Yahoo!360这一社交网络的密度演化。所用的数据是从该网站开始建立到第40周的数据。从图4b可以发现:网络有3个清晰的阶段:起初增加到一个峰值然后开始减小,最后逐渐稳步增加。文献解释了其中的原因:社交网络建立后,存在少数对该网络有好奇心的人加入,并疯狂地邀请许多朋友来加入体验,这引起了第一个阶段的高峰期。第二阶段对应于这种新鲜感自然衰减,导致网络密度的下降。第三阶段对应于网络真正的有机增长(当越来越多的人知道了该网络时)。越来越多的人加入该网络,节点和边的增加最终使得密度稳步上升。对比图4a图4b,“冰桶挑战”网络的密度并没有出现图4b的3个阶段,并且最大值也就达到0.12左右,而Yahoo!360网络的密度最大达到0.9多,最小的也在0.3左右。分析其中的原因:“冰桶挑战”网络的密度并没有增加,原因是该网络是点名亲密好友关系的网络,不是所有好友,边数增加是有限的,所以网络密度不会增加。然而Yahoo!360网络节点之间的关系是非常稠密的,因为用户可以邀请他所有的朋友加入,但是其中的强关系是非常稀少的。
2.3.2聚类系数
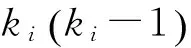
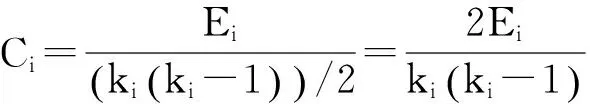
(2)
其中,Ei为节点i的ki个邻居节点之间事实存在的边数。
在一个网络中,聚类系数是衡量网络中一个节点的邻居间紧密程度的一个指标,用来考察节点及其邻居所呈现出来的结构。大多数真实网络比如Facebook、Twitter、人人网及新浪微博等都表现出聚集结构。
本文计算出网络前6天的平均聚类系数,如图5所示。
从图5a中不难发现,聚类系数在前两天为0,接着迅速增加,到后面又开始减小。分析其中的原因:可以看出网络在形成初期,并没有形成三角关系,而是类似于星型结构,发散出去。如果按照既定规则演化网络的聚类系数会一直为0,节点不会出现三角关系。然而该网络演化到一定程度,在第3天时聚类系数变为0.016 7并且开始增加,网络出现了三角关系,意味着实际网络出现了共同好友关系。在现实中,由于人际关系的影响人的亲密朋友可能不止一个,在信息传播过程中由于获取信息不及时等原因,被多个好友点名的情况就会发生,所以随着该网络的演化,聚类系数就变为非零值。网络节点在增加的同时,整个网络中挑战者间彼此成为好友的机率也增加导致聚类系数不断增加。而后平均聚类系数有所减小,说明网络扩展速度变快,网络变得发散,导致网络的平均聚类系数减小。
Bimal Viswanath研究了Facebook这一社交网络的演化。搜集到的数据为2006年9月至2009年1月的数据。图5b为文献[14]中Facebook社交网络的聚类系数演化过程。横坐标表示2007年及2008年不同的月份。从图中不难发现,Facebook网络的聚类系数平均在0.13左右。然而,本文研究的网络集聚系数最大达到0.02左右,要比Facebook网络小的多。分析其中的原因:首先Facebook网络的数据是网络诞生后中间时间段的数据,而在网络中朋友间一旦建立好友关系,就不会有很大变动。本文网络聚类系数具有明显的变化,是因为在网络形成初期,朋友关系会因为节点的不断加入而发生变化。其次,Facebook网络考虑了用户的所有关系,本文的网络只有强关系,所以聚类系数相对较小。
2.3.3网络效率与最大连通子图
网络中两个节点i和节点j之间的最短路径是指连接着两个节点的边数最少的路径。两点间的距离dij定义为连接着两个节点的最短路径上的边的数目。对于不连通的网络,可能两个节点之间不存在连通的路径,即意味着这两个节点之间的距离为无穷大,从而导致整个网络的平均路径也为无穷大。为了避免这种情况,定义一个网络的平均效率[15]:
(3)
其中,N为网络中节点个数,dij为节点i到节点j的距离。两个点之间的距离越短那么两点之间信息传递的效率则越高,即效率与两点距离成反比关系。
网络的连通子图体现了一个网络的连通比率,对于分析信息在网络中的传播有重要的作用,研究网络动态演化有着重要的意义。本文计算得到了6个网络的效率如图6a所示及每个网络的子图数量和最大连通子图节点的个数,如图6c~d所示。
根据网络效率的定义也可以看出网络效率受到网络子图个数的影响,当网络中子图较多时网络效率就会变小。具体分析,从图6a中可以发现前3个网络的效率由开始的0.214 3变为0.058 8又到0.039 9逐渐变小,且第2个网络比初始网络减小了81.4%。开始时网络的节点数较少,不连通子图数量也较少,节点间相互达到的路径很短,因此网络效率较高。随着新节点的不断加入,不连通子网不断增加导致节点间的路径变得较大,网络效率变小。随后网络效率从0.098 9到0.125 9变大,随着网络的不断扩大,网络的密度变大因此效率就会增加。最后又有减小趋势到0.121 8,同样也受到网络规模的影响,节点间的路径变长。同样,图6b为文献[14]中Facebook社交网络的平均路径长度演化过程。从图不难发现,Facebook网络节点间的平均最短路径在7左右不会有很大变化,而本文网络效率到最后也趋于稳定在0.12左右。分析两者异同的原因:当网络演化到一定程度时,网络中每个节点的连边基本不会发生太大变化,使得网络效率或者最短路径趋于稳定。而本文网络由于节点连接边较少、连通子图数量较多等原因使得网络效率较低。
观察图6a与图6b不难发现,网络效率与连通子图数有很大相关性。即网络效率下降时网络子图数量增加,当网络效率上升时,网络子图数量减小,说明网络子图数量影响网络效率的变化。从图6b中网络子图数量的演化可知,在网络形成初期网络子图数量迅速增加,由3变为10到18,说明该事件能够得到很多人的响应,自愿加入到网络中。而后又有减小的趋势,说明网络连通性变好,一方面说明自愿挑战者的数量减小,另一方面可能是很多独立网络连接到了一起,在现实中朋友关系更加密切。从图6c也不难发现最大连通子图的节点数量不断增加,说明很多独立子网络很快融入到最大子网络里,形成一个连通网络。
3总结与展望
社交网络的形成与演化从一定程度上来讲是人际关系的不断延伸,是一个复杂的过程,现实的和虚拟的各种因素相互影响,呈现多种特征。
本文主要从“冰桶挑战”这一事件出发,构造了一个真实的社交网络。搜集从网络形成到第六天的数据,从网络规模等研究了该网络的演化过程。通过分析发现该网络密度不断减小;聚类系数从初始值零增加到0.016 7后又缓慢减小;网络效率从0.214 3开始减小,最大减小量为初始值的81.4%,后又缓慢增加;连通子图的数量从3迅速增加,最高增加了初始值的5倍,后又减小。本文发现连通子图的数量与网络效率呈负相关关系。从这些结论中,可以清楚看出这一特殊网络的演化过程,为社交网络演化模型的建立提供一定依据。本文也与其他大型社交网络的演化做了对比分析,从中也可以得出本文社交网络演化的特殊性。
对于包括社交网络在内的复杂网络而言,结构与演化动力学的研究正逐渐成为热点。复杂网络的研究重点也逐渐转向基于结构的信息传播演化过程。只有理解了在这种结构上的传播机理后,才能够有根据地进行传播的控制问题研究。在现实世界中,一些事件的发展社会媒体起到了很大的作用,而如何量化社交媒体的作用也是一个亟待解决的问题。本文在获取“冰桶挑战”数据的过程中,只搜集一些名人的数据,对于很多参与挑战的普通人并没有考虑在内,这样难免会影响到网络的演化过程。另外,对于在统计数据时由于有时间差有些数据难免会有所遗漏,从一定程度上影响了结论的精确度。
参考文献:
[1]斯坦利·沃瑟曼,凯瑟琳·福斯特. 社会网络分析: 方法与应用[M]. 陈禹,孙彩虹,译. 北京: 中国人民大学出版社, 2012.
[2]Dodds P S, Muhamad R, Watts D J. An experimental study of search in global social networks[J]. Science, 2003, 301(5634): 827-829.
[3]Shin D H. The effects of trust, security and privacy in social networking: a security-based approach to understand the pattern of adoption[J]. Interacting with Computers, 2010, 22(5): 428-438.
[4]MisloveA, Marcon M, Gummadi K P, et al. Measurement and analysis of online social networks[C]//Proceedings of the 7th ACM SIGCOMM Conference on Internet Measurement. ACM, 2007: 29-42.
[5]Hellmann T, Staudigl M. Evolution of social networks[J]. European Journal of Operational Research, 2014, 234(3): 583-596.
[6]Watts D J, Strogatz S H. Collective dynamics of ‘small-world’networks[J]. Nature, 1998, 393(6684): 440-442.
[7]Newman M E J, Watts D J. Renormalization group analysis of the small-world network model[J]. Physics Letters A, 1999, 263(4): 341-346.
[8]Barabási A L, Albert R. Emergence of scaling in random networks[J]. Science, 1999, 286(5439): 509-512.
[9]张立, 刘云. 虚拟社区网络的演化过程研究[J]. 物理学报, 2008, 57(9): 5419-5424.
Zhang L, Liu Y. Research on the evolution process of virtual community networks[J].Acta Physica Sinica, 2008, 57(9): 5419-5424.
[10] 熊熙,曹伟, 周欣, 等. 社交网络形成和演化的特征模型研究[J]. 四川大学学报: 工程科学版, 2012, 44(004): 140-144.
Xiong X, Cao W, Zhou X, etal. Research on the feature model of the formation and evolution of social networks[J]. Journal of SichuanUniversity(Engineering Science Edition), 2012, 44(004): 140-144.
[11] Kumar R, Novak J, Tomkins A. Structure and evolution of online social networks[M]//Link Mining: Models, Algorithms, and Applications. Springer New York, 2010: 337-357.
[12] 郭海霞. 新型社交网络信息传播特点和模型分析[J]. 现代情报, 2012, 32(1): 56-59.
GuoHaixia. New Social networking features andmodel analysis of information dissemination[J]. Journal of Modern Information, 2012, 32(1): 56-59.
[13] 汪小帆,李翔,陈关荣.网络科学导论[M].北京:高等教育出版社,2012.
[14] Viswanath B, Mislove A, Cha M, et al. On the evolution of user interaction in Facebook[C]//Proceedings of the 2nd ACM Workshop on Online Social Networks. ACM, 2009: 37-42.
[15] Latora V, Marchiori M. Efficient behavior of small-world networks[J]. Physical Review Letters, 2001, 87(19): 198701.
(责任编辑李进)
The Evolution of Social Networks Constructed by “Ice Bucket Challenge”
YANG Kai, LIU Xiaolu, LIN Jianhong, CHENG Xi, GUO Qiang, LIU Jianguo
(Research Center of Complex Systems Science, University of Shanghai for Science and Technology, Shanghai 200093)
Abstract:The evolutionary process of social networks at initial period is very important, especially for the quantitative understanding of the formation and the evolution of interpersonal relationships. In this paper, combining with the “Ice Bucket Challenge”, we collect the data of this event from the launch to the sixth day in our country. The nodes stand for the challengers and the edges are the relations of called people in the social networks. By analyzing the rules of the structural characteristics, including the network size, the clustering coefficient, density, network efficiency and connectivity sub-graphs, we find that the clustering coefficient increased from zero to 0.0167 at the beginning and then decreases; the densityof the network declines from 0.1209 over time; the network efficiency reduces by 81.4% at first and then slowly increases; the connected sub-graphs rapidly increases five times and then decreases; the network efficiency and the number of sub-graphs are negatively correlative. Taking into account the specificity of the network,we compare with evolution of other social networks.Thiswork will be helpful for understanding the law of the formation and development of the early social networks.
Key words:social networks; network evolution; topological structure; Ice Bucket Challenge
文章编号:1672—3813(2016)02—0090—07;
DOI:10.13306/j.1672-3813.2016.02.011
收稿日期:2014-10-29;修回日期:2015-01-12
基金项目:国家自然科学基金(71171136,61374177,71371125);上海市一流学科建设项目(XTKX2012);教育部人文社科基金(13YJA630023);上海出版传媒研究院开放基金(SAYB1407)
作者简介:杨凯(1987-),男,山东泰安人,博士研究生,主要研究方向为在线社会网络结构与演化分析。 通讯作者:刘建国(1979-),男,山西临汾人,教授,主要研究方向为网络科学,商务智能,知识管理。
中图分类号:N941
文献标识码:A

