移动P2P社会网络中关键节点发现方法*
白宇清,李海健,蔡青松+
1.北京工商大学计算机与信息工程学院,北京1000482.廊坊师范学院数学与信息科学学院,河北廊坊065000
ISSN 1673-9418 CODEN JKYTA8
Journal of Frontiers of Computer Science and Technology 1673-9418/2016/10(03)-0350-13
移动P2P社会网络中关键节点发现方法*
白宇清1,李海健2,蔡青松1+
1.北京工商大学计算机与信息工程学院,北京100048
2.廊坊师范学院数学与信息科学学院,河北廊坊065000
ISSN 1673-9418 CODEN JKYTA8
Journal of Frontiers of Computer Science and Technology 1673-9418/2016/10(03)-0350-13
E-mail: fcst@vip.163.com
http://www.ceaj.org
Tel: +86-10-89056056
* The National Natural Science Foundation of China under Grant Nos. 61170296, 6137309 (国家自然科学基金); the Beijing Committee of Science and Technology Program under Grant No. KM201110011004 (北京市教委科技计划); the Collaborative Innovation Centre for State-Owned Assets Administration of Beijing Technology and Business University under Grant No. GZ20131102 (北京工商大学国有资产管理协同创新中心项目).
Received 2015-09,Accepted 2015-11.
CNKI网络优先出版: 2015-12-03, http://www.cnki.net/kcms/detail/11.5602.TP.20151203.0922.004.html
摘要:传统的消息传播关键节点发现方法大多针对静态网络进行研究。针对移动P2P社会网络这类复杂的动态时变网络,提出了一种其时效性随时间和传播路径衰减的一般类型消息传播过程中关键节点的发现方法。将静态网络中基于通路(walk)的节点中心性分析方法扩展到移动P2P社会网络中,将消息传播路径分解到时间-空间两个维度上,并利用两个衰减因子分别刻画消息的效用随传播路径长度衰减及随时间推移衰减这两种自然特性,利用节点的历史相遇信息,得到了节点传播能力的量化分析函数,以此刻画节点对时效性消息的相对传播能力。基于真实Trace数据的实验结果验证了该方法的可行性。由于所述方法考虑了消息时空两个维度上所有可能的传播路径,也可用于有效预测网络的演化和不同节点在未来传播或获取消息时的相对重要程度。关键词:移动P2P社会网络;实时消息传播;中心性分析方法;动态通路
1 引言
近年来,随着具有短距无线通信能力(如Blue-Tooth、Wi-Fi、Zigbee等)的移动智能设备(诸如智能手机、PDA、可穿戴设备)的大规模普及,人们日常生活中的相遇信息可以几近完整地记录下来,这不仅促进了传统社会网络[1]及机会网络[2]在信息感知、处理和传播等领域的研究,也使得对人的真实社交情形进行更加深入的研究,以提出更加高效的消息传播机制成为可能。
随着移动互联网的兴起,作为社会网络和机会网络相结合的产物,移动P2P(peer-to-peer)社会网络[3]日益受到研究学者的关注,成为无线网络领域的又一研究热点。移动P2P社会网络是一类节点间通过对等通信自组织组网形成的网络。该网络的节点是具有短距无线通信能力的移动智能设备。设备虽无法自主移动,但依赖其载体(人)的社会性移动,设备间可发生相遇并进行信息交换,使这种通信模式具有典型的社会性特征。移动P2P社会网络主要针对人的社会属性或人的移动性对网络动态性的影响,人的社会关系演化对网络形态演化的影响,如何利用人的社会性或移动性提升网络消息传播效率等方面内容[4]进行研究。移动P2P社会网络的相关研究不仅可应用于传统社会网络所涉及的瞬态社交网络、基于情景的移动社交、基于个体特性的广告推送等方面[5],还对城市规划、疫情扩散、社会关系挖掘与分析等领域有重要指导意义[6]。在如今这个社交活动从娱乐化向工具化过渡的时代,移动P2P社会网络无疑具有良好的研究前景和应用价值。而“追踪、发现对消息传播有关键作用的节点”这类问题,一直是该领域的热点问题。
移动P2P社会网络是复杂网络的一种,一方面该类网络节点数目众多,另一方面该类网络节点因具有复杂的社会属性而使节点的移动模式复杂多变,最终导致节点具有较强的动态性。在移动P2P社会网络中,节点间几乎不存在完整的端到端路径,节点不依靠固定的基础设施,采用“存储-携带-转发”的数据传输模式,利用智能设备的短距通信接口以自组织的方式与其他设备发生相遇而交换信息。由于节点在各自的社会性上存在差异,导致节点的移动性不同并有不同的相遇模式,最终使不同节点有不同的消息传播与消息获取能力。如何在这类网络中发现消息传播的关键节点,并利用其提升网络消息传播效率成为研究学者们普遍关注的问题。
在已有的复杂网络研究工作[7-8]中,学者借助社会网络分析法(social network analysis,SNA)提出诸如Katz中心度、节点度中心性等测度,用于衡量节点在信息传播过程中的重要性。但这些研究大多通过叠加历史相遇数据将网络抽象为一个静态网络来处理,因此这些方法未能完全体现网络的重要特征——网络动态性与时变演化性。实际场景中,由于人的频繁社会活动使得节点之间的相遇关系随时间不断动态变化,利用叠加图的方法会造成大量重要相遇信息的缺失,无法准确刻画网络的演化过程。如图1所示,随着时间推移及网络演化,从拓扑角度来看,节点A或节点B都能够将消息逐跳地、间接地传递给节点F,但是节点F却不能将消息传递给节点A或节点B;而使用传统的叠加图刻画网络后,从其拓扑结构看,节点A或节点B与节点F间均存在可达路径,表示节点A或节点B与节点F均可进行双向信息传递。出现这种错误是由于叠加图中未能体现网络演化的时向性。
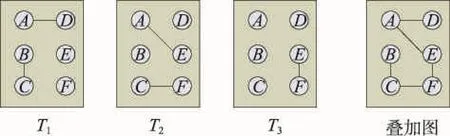
Fig.1 Time-ordered snapshots and overlapping graph图1 时间快照与叠加图演示
移动P2P社会网络是网络拓扑随时间不断变化的时变动态网络,为准确刻画其拓扑演化过程,本文利用时间演化图模型(time evolving graph,TEG)对其进行建模分析。TEG模型将动态演化的网络抽象为随时间不断变化的一系列拓扑快照序列,每个快照刻画一个时间间隔内的网络状态。需要说明的是,快照间时间间隔的选取方法是目前仍无定论的问题[9],本文一方面根据经验值,一方面根据具体的网络情景选取相应的时间单位进行拓扑快照的划分。
节点间传递一个消息等效于节点间产生或传递一个影响,节点可对其他节点产生的总影响称为节点的影响力[7],而节点的中心性是表示节点影响力大小的常用测度[8]。故本文使用节点的中心性测度作为其在网络中传播消息时的关键程度的衡量指标。传统基于通路(walk)的节点中心性分析方法,因静态网络不涉及时间因素,实质为只计算空间维度上的所有长度通路(可理解为一张快照上的通路)的加权和。与之不同,本文同时考虑空间维度和时间维度上的所有长度通路(即动态通路,包含只涉及某一快照的通路和涉及多个快照的通路)的加权和来体现某一节点对网络中其余节点的影响力大小。利用通路而不是“路径(path)”或“最短路径(the shortest path)”进行计算是因为移动P2P社会网络中的节点动态性较强,节点间难以长时间维持稳定的通信链路,而消息在每个节点上的存储一般具有一定时长的生存期,节点会充分利用每次的相遇机会进行最大功率的信息传输来保证将更多的消息传递出去。这种数据传输模式必然导致消息在传递过程中会经过重复的节点或重复的边,而通路恰可以正确刻画这种消息传递路径。另外,本文在考虑对不同长度动态通路进行不同程度衰减的同时,也考虑节点间相遇的前后关系以及消息的实时性,利用时间衰减因子对等步长但产生时间相对久远的动态通路进行更大程度的衰减。这样做的原因在于节点对网路中其他节点产生的“旧影响”应当随时间推移逐渐变得不再重要,即网络中的“旧消息”的影响力应当随时间推移而衰减。
本文针对移动P2P社会网络这类动态时变网络,借助SNA方法,并结合静态物理学中计算粒子之间弹性势能的“格林函数”方法,将静态网络中基于中心性指标的分析方法扩展到移动P2P社会网络,利用两种衰减因子分别刻画消息的效用随传播路径长度衰减及随时间推移衰减这两种自然特性,利用节点的历史相遇信息,提出一种节点传播能力的量化分析函数,刻画节点对时效性消息的相对传播能力。本文考虑消息的实时性,一方面有助于量化分析节点传播实时消息的能力,另一方面通过历史数据对一段时间内的节点消息传播能力进行综合考虑,可识别出“最近较活跃”的节点,将其作为实时性消息传播的关键节点从网络的众多节点中挑选出来。基于真实Trace数据的实验表明,本文方法可快速准确计算出各节点的消息传播关键程度,且当利用本文方法选出来的关键节点作为消息传播的起始节点时,网络的消息覆盖速率明显提升。另外本文方法考虑了消息时空两个维度上所有可能的传播路径,因此也可用于有效预测网络的演化和不同节点在未来传播或获取消息时的相对重要程度。在某些网络环境下,当衰减因子取值恰当时,本文方法的预测准确度最大可接近90%。
2 相关研究工作与现状
移动P2P社会网络由机会网络和社交网络结合而产生,是具有显著的拓扑动态性和演化性的一类复杂网络。复杂网络领域已有的研究工作[10-11]等用于研究人的移动性问题。基于这些工作,文献[12-13]提出了基于节点不同连接机制的机会消息传递方法。但是由于人移动性具有不可预知性使得网络呈高度动态性,在移动P2P社会网络中研究拓扑演化规律以及发现消息传播的关键节点成为一类极具挑战性的问题。随着针对该领域研究的增多,准确刻画网络形态的问题受到更多的关注。文献[14]提出了随机图的概念,然而由于随机图的边独立性,使其不能很好地应用于动态网络分析。而文献[15]提出的时间演化图模型则受到普遍的关注。该模型不同于静态图论与随机图,向网络中引入时间因素,将动态演化的网络沿时间方向刻画为离散的拓扑快照序列。该模型可用于在相邻快照间研究拓扑演化特性,并可在单一快照内研究节点的空间拓扑关系。
针对网络内的关键节点发现问题,许多研究利用SNA方法提出基于中心性的研究方法[7-8],给出诸如度中心性、Katz中心性等测度。但中心性度量方法最初是基于静态网络提出的,因此并不直接适用于移动P2P社会网络这类动态网络。在移动P2P社会网络中,因节点具有的个体社会性差异,使得其在消息传播能力上也存在一定的差异,研究工作[16]针对该问题利用真实相遇数据验证了这一观点,但是并未提出有效的分析模型或关键节点发现方法。已有的研究[17]将基于通路的中心性分析方法从静态网络中扩展到动态网络中,利用Katz中心度衡量节点的影响力大小。但是该方法的参数对快照拓扑形态的依赖性较大且不具有弹性,并不易于利用。研究工作[18]针对Email网络研究了消息随时间传播效应递减的情况,提出了评估节点传播能力的方法。
上述工作大多基于通路以及中心性的概念对节点的影响力或消息传播能力进行度量,其缺陷主要集中于两个问题:(1)上述有些工作基于静态网路研究,不适用于动态网络分析;(2)有些工作并未考虑网络演化的时间因素,即消息的实时性或节点之间产生影响的先后关系。本文为尽量改正上述缺陷,在网络动态性极强,节点之间消息传递强烈依赖于相遇机会的移动P2P社会网络中,将传统的静态网络分析方法扩展到动态网络的同时,充分考虑消息的实时性及节点间产生影响的先后顺序,提出移动P2P社会网络中传播实时消息的关键节点发现方法,并利用真实环境采集的Trace数据对方法进行了验证。
3 系统建模
3.1静态网络中节点的中心性
图G=(V,E)表示一个包含n个节点m条边的无权简单静态图,V定义为节点集合且|V| =n,E定义为节点之间连边的集合且|E| =m (m,n∈Z+)。图G对应的n×n维邻接矩阵表示为Α=aij(i,j∈V),当节点i、j之间存在连边时aij=1,否则aij=0。由于图G为无权简单静态图,故aii=0。
本文利用通路而不是“路径”或“最短路径”进行计算是因为移动P2P社会网络中的节点因其载体的社会性而具有高度动态性,节点间几乎不存在完整端到端路径,并且难以长时间维持通信链路的稳定。节点采用“存储-携带-转发”的数据传输模式,而每个节点一般只在一定时长的消息生存期内携带该消息,故节点会充分利用每次的相遇机会进行最大功率的信息传输来保证将更多的消息传递出去。这种数据传输模式必然导致消息在传递过程中会经过重复的节点或重复的边。“路径”或“最短路径”均不存在重复的边或点,而通路却可以正确刻画这种消息传递路径。现给出静态网络中通路的定义。
定义1(通路)静态图G=(V,E)中(V={v1,v2,…, vn},E={e1,e2,…,en})的通路表示为一个顶点与边交替出现的序列,即若节点i、j之间存在vie1v1e2…ewvj这样一个序列,则表示节点i、j之间存在一条通路。
引理1若邻接矩阵Α的w (w∈Z+)次幂为Αw,其i、j位置为k(即(Αw)ij=k),表示节点i、j之间长度为w的通路条数为k条。
本文旨在找到消息传播的关键节点,而节点的关键程度等效于节点在网络中的影响力大小,本文借助SNA方法,使用中心性指标表示节点的影响力大小。节点对网络中其余节点的影响力越大,该节点与网络其余节点产生联系的可能性越大,节点之间的消息传递越容易完成,节点对于消息传播的关键程度越大。节点间产生联系以及节点间进行消息传递的过程均是沿节点间的通路发生的,通路长度越长,节点之间产生联系或进行消息传递途经的节点越多,产生影响或完成消息传递的难度越大。故本文按照“长步长通路衰减更多,短步长通路衰减较少”的原则对不同长度的通路设置不同权重。本文使用n×n维矩阵S表示节点对网络中的其余节点的影响力矩阵,Sij表示节点i对节点j的影响力大小。Sij的值越大,节点i对节点j的影响力越大,节点i与节点j产生联系或节点i向节点j成功传递消息的可能性越大。(S1)i表示节点i的中心性指标,即节点i在网络中的总影响力大小。(S1)i越大,节点i在网络中的影响力越大,节点i的作用越关键。其中1是n×1维向量1=(1,1,…,1)T。最终,按照通路计算方法及上述衰减原则可得到下式:进而使用S1、(S)1分别表示传播、获取消息的关键程度。
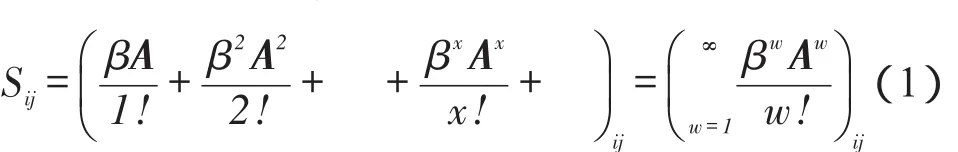
由式(1)可知,Sij将由节点i开始并在节点j结束的所有长度的通路按其长度进行衰减并求加权和。从另一角度来看,通路的长度可表示节点之间关系的亲密程度,经历较短步长产生联系的节点之间的亲密程度要比经历较长步长的节点之间的亲密程度更强,故Sij为长步长通路赋予较小权重,为短步长通路赋予较大权重,表示节点对与其关系更紧密的节点有更大的影响,或消息在关系亲密的节点之间更容易传播。让长度为w的通路按照的方式衰减。式(1)通过级数运算变换为式(2):
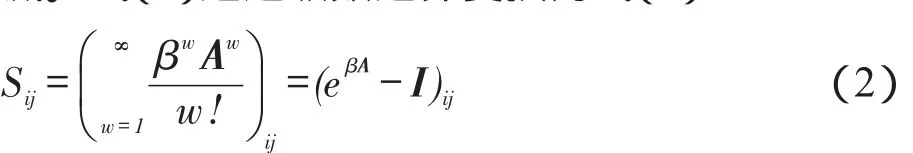
本文为不同长度通路设置权重的思路来源于静态物理学中计算粒子之间弹性势能的“格林函数”。“格林函数”应用于这样的一个网络:节点彼此之间由弹簧连接并处于同一水平面上,在起始时刻弹簧处于自然松弛状态,在之后的某一时刻,将某一个节点向上提拉到一个高度,网络中的其他节点在弹簧的牵引下也会各自被拉伸到某一高度,此时弹簧处于拉伸状态,节点间因弹簧的连接而产生了弹力。“格林函数”用于计算该类网络中节点间的弹性势能。移动P2P社会网络与上述网络有很大的相似性,移动P2P社会网络中的节点之间也存在类似于“弹簧”这样的关联——社会关系,节点间因各自社会关系而彼此关联,社会关系紧密程度直接决定节点间的相遇频度以及节点间的相互影响程度。本文借鉴这种思路,利用“具有不同社会关系紧密程度的节点间会产生不同程度的相互影响”作为评判节点在网络中关键程度的依据是合理且是可行的。
t+1t+1T
3.2动态演化网络中节点的中心性刻画
移动P2P社会网络是动态性极强的一类网络,节点的社会性移动使节点之间的连边在不断产生和消失。为最大程度捕捉网络的动态演化性,本文利用时间演化图模型对该类时变网络进行建模和分析,使用中心性指标作为判断节点关键程度的依据,并将传统的基于通路的中心性计算方法扩展到时变网络中。此处首先给出时间演化图的定义。
定义2(时间演化图)对于任意节点集|| V =n,令T⊆[Tstart,Tend]为起始时间Tstart、终止时间Tend上的任意时间集合,Δt=(ti,ti+1]∈T(i∈Z+)为快照间隔。若令Gi=(V,Ei)为时间间隔(ti,ti+1]内定义在节点集V上的子图,则g:={Gi}为定义在区间[Tstart,Tend]上的时间演化图。
根据定义2,给定快照时间间隔Δt,演化图g:={Gi}由一系列沿时间方向构成的静态快照组成,其对应的邻接矩阵序列可表示为{Ai}。为将前文所提的静态网络中的中心性度量方法扩展到动态网络中,需要将通路的概念引入到时间演化图中。在此给出动态通路的形式化定义。
定义3(动态通路)定义在一个非递减的离散时间序列t1≤t2≤…≤tr≤…≤tk(t1,tk∈T)上的顶点与连边的序列vie1v1e2…vmervm+1…ewvj构成节点i到节点j的长度为w的动态通路,当且仅当第r个快照的邻接矩阵满足(Αr)imim+1≠0。
在移动P2P社会网络中,因为节点采取“存储-携带-转发”的数据传输模式,所以节点间不仅在同一拓扑快照内会产生联系,也可以跨拓扑快照产生联系。如图1所示,节点B在前两个时间快照内没有与节点F发生直接接触,但是节点B在T1时刻将消息传给节点C,由节点C携带节点B的消息在T2时刻和节点F发生相遇时,将节点B的消息传给节点F。即通过节点C,节点B与节点F间完成了消息传递,或说通过节点C,节点F受到了节点B的间接影响,而节点B和节点C间在T1时刻产生了直接影响。节点之间的直接影响沿空间维度上的通路传递,间接影响沿时间维度上的通路传递。将空间维度和时间维度上产生的通路统称为动态通路,并将其明确地分为相对应的两类:空间通路与时间通路。空间通路是在某单一静态快照中形成的通路,而时间通路由若干个连续(亦可不连续)快照的通路组成。
本文将判定节点在网络中关键程度的中心性指标Sij的计算思路扩展到移动P2P社会网络中。将节点间产生的所有长度动态通路进行加权求和,并且依旧按照“长步长通路赋予较小权重,短步长通路赋予较大权重”的方式得到节点在移动P2P社会网络中的动态中心性指标矩阵Dt,(Dt)ij表示截止到第t个拓扑快照,节点i、j之间的影响力大小。特别的,因为节点采取“存储-携带-转发”的数据传输方式,当节点在当前快照无法将消息传递给另一节点时,节点将在该快照内继续“携带”该消息,即节点把消息传递给自身,所以在计算动态中心性指标Dt时,在节点的动态通路加权公式中加上n×n维矩阵I,表示节点把消息传递给自己。最终,得到如下公式:

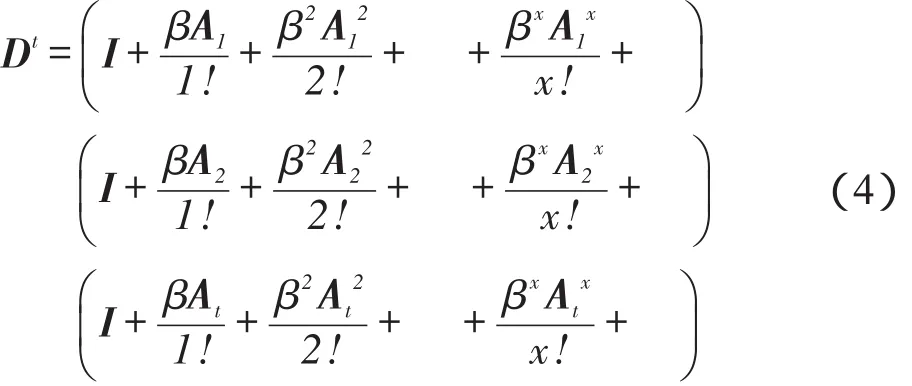
式(3)展开为式(4)后不难发现,式(3)考虑了所有的动态通路组合:(1)在同一拓扑快照内起始和终止的所有长度的通路;(2)不同拓扑快照内起始和终止的所有长度的通路。在同一拓扑快照内长度为w的通路按照βww!的方式衰减,利用不同拓扑快照完成的长度为w的通路按照βw(l1!l2!…lr!)的方式衰减,其中w=l1+l2+…+lr表示跨越了r个拓扑快照完成了长度为w的通路,并在第r个拓扑快照中完成了w中的lr步。
3.3动态网络中节点对时效性消息的传播能力度量
虽然式(3)对等步长的时间通路和空间通路进行了不同程度的衰减,但是这种方法依旧存在缺陷:这种衰减方式只按照通路长度对时间通路与空间通路进行衰减,并未体现节点之间产生影响的先后顺序或消息的实时性,即未考虑动态通路产生的时间先后顺序。特别地,可把节点之间的影响与消息的实时性看为是等效的。这是因为节点之间传递了消息即是节点之间产生了影响,消息的实时性亦即是节点之间产生的影响的实时性。
在实际中,节点之间产生影响的先后顺序或消息的实时性是十分重要的。节点之间的影响强度或消息效用往往随时间推移而递减。即使消息(影响)传递历经的动态通路长度相同,但最近或当前发生的事件或某一节点对另一节点最近产生的影响往往重要程度更高。人们更重视“最近”发生的事件或“最新的”消息,而不是传播了相同的动态通路长度的很久之前发生的事件或传播了很久的“旧消息”。故本节考虑节点之间消息(影响)的实时性,使用tk表示第k个快照中产生的动态通路的“发生时刻”,“发生时刻”越大,表示该时刻距“当前时刻”越近,该时刻产生的影响越重要,该时刻产生的动态通路应受到较少的衰减。
综合考虑上述问题,本文使用节点在网络中的影响力大小(节点中心性指标)作为评判节点关键程度的评价指标,提出传播实时消息的关键节点发现的迭代计算公式:
Qk+1=(e-αΔtk+1Qk+I)(eβAk+1
+I)-I(5)式(5)是迭代式,其中Δtk+1=tk+1-tk,k∈Ν,Q0=0。本文利用n×n维矩阵Qk表示截止到第k个快照时移动P2P社会网络中节点的影响力矩阵,第k个拓扑快照网络对应的邻接矩阵表示为Αk。本文对时间因素按照自然指数方式进行衰减,设置时间衰减因子α,且α可根据网络的实际情形对衰减程度进行调节。利用e-αΔt对不同静态快照中的通路按照快照产生的先后顺序进行衰减,并保证同一个静态快照中不同长度的空间通路在时间维度上的衰减程度相同。另外,Qt+11、(Qt+1)T1分别表示节点传播、获取实时性消息的关键程度。
下文给出式(5)能够正确计算移动P2P社会网络中节点之间影响力的说明,并利用数学归纳法证明其正确性。
证明当k=0时,Q1=eβA1表示当前只有一个快照且Q0=0(迭代式的初始值),所有通路的起始和终止全部发生在快照Α1(此时网络中只有空间通路)。该式和式(3)的含义相同。
当k=1时,Q2=(e-αΔt2eβA1+I)(eβA2
+I)-I,展开后
得到Q2=e-αΔt2eβA1eβA2
+e-αΔt2eβA1
+eβA2
,公式中第一部分表示在快照Α1起始并在快照Α2结束的所有长度的时间通路的加权和;第二部分表示在快照Α1起始并终止的所有长度的空间通路的加权和;第三部分表示在快照Α2起始并终止的所有长度的空间通路的加权和。由以上3个部分作为计算截止到第2个快照的节点间影响力的计算元素,一方面考虑了所有长度动态通路的起始终止的可能性的组合,另一方面考虑了不同动态通路产生的时间前后因素。
设k=s时,Qs+1=(e-αΔts+1Qs+I)(eβAs+1
+I)-I成立。则k=s+1时,考虑所有动态通路起始和终止的情况和其所有长度情况时有:
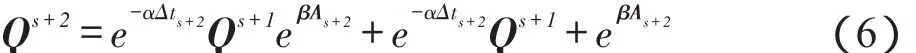
公式中第一部分表示延续k=s时的情况,并在第s+2个拓扑快照又前进了m(m≥0,m=0时表示节点将信息传给自己)步新形成的动态通路加权和;第二部分表示截止到第s+1个拓扑快照,在之前任一拓扑快照中起始并在之后任一拓扑快照中终止的所有长度的时间通路的加权和;第三部分表示在第s+2个拓扑快照起始并在该快照中终止的所有长度的空间通路的加权和。进一步化简可得:
Qs+2=(e-αΔts+2Qs+1+I)(eβAs+2
+I)-I(7)即得证式(5)成立。
4 实验验证
4.1实验数据
为验证本文提出的传播实时消息的关键节点发现方法的有效性,采用CRAWDAD[19]提供的从真实环境采集的Trace数据对本文方法进行若干验证。选取基于两种常用无线通信接口Bluetooth与Zigbee于真实环境采集的数据进行实验。Bluetooth接口是较常用的通信接口,Zigbee虽然不是智能终端的标准配置,但由于它通信连接耗时更短(毫秒级),通信耗能更少等特点,从而具有良好的应用前景。这两种短距通信接口的物理特性使其采集的数据可以较准确地刻画移动P2P社会网络的网络情形,且这两种通信接口是移动P2P社会网络消息传输较为理想的选择,具有较大的应用前景。
本文实验所用的数据集具体为:(1)记录2009年Sigcomm会议期间,100个持有HTC s620手机的用户利用Bluetooth接口相遇的数据;(2)记录2008年在圣安德鲁斯大学校园内27名携带传感器的人员在79天内通过Zigbee接口相遇的信息。两组数据利用两种不同的通信接口,分别展示了会议场景及校园场景这两种不同的数据采集环境的不同网络特性。针对这两种具有差别的数据集进行实验,可验证本文方法具有普遍适用性。表1列出了实验数据的基本信息。
4.2不同节点的消息传播效率
网络中不同个体的社会属性决定了其对消息具有不同的传播能力。本文提出了传播实时消息的关键节点发现方法,旨在找到并利用这些关键节点提升网络的消息传播效率。为验证这一目的,首先利用本文方法针对各个数据集分别找到消息传播时关键程度最强与最弱的两个节点,之后分别将这两个节点作为消息传播的源节点,在网络中进行洪泛(flooding)。由于在移动P2P社会网络中节点间是间歇性连通的,洪泛方式因具有冗余分发等特性,使其对动态网络具有较好的自适应性,可以比较准确地刻画基于通路的消息分发,故本实验选取洪泛方式进行消息传播。另外,研究工作[20]表明:2-copy(对同一消息而言,节点对其至多转发2次)与无限副本洪泛方式的网络覆盖速率几近相同,本实验利用2-copy洪泛方式来降低消息传播过程中的网络开销。为了使实验结果更加直观,本实验计算出网络覆盖率的平均情况,与特定节点为消息源时的网络覆盖率进行对比。从图2给出的实验结果可看出:利用本文方法选出的关键程度最强的节点作为消息源头进行消息传播的速率明显是最快速的。该实验结果清晰表明,利用本文提出的方法作为传播实时消息的关键节点发现方法,可以提升网络的消息覆盖速率。网络消息覆盖速率提升,表示实时性消息可快速地被传递给网络中的各个节点。

Table 1 Dataset description表1 数据集信息
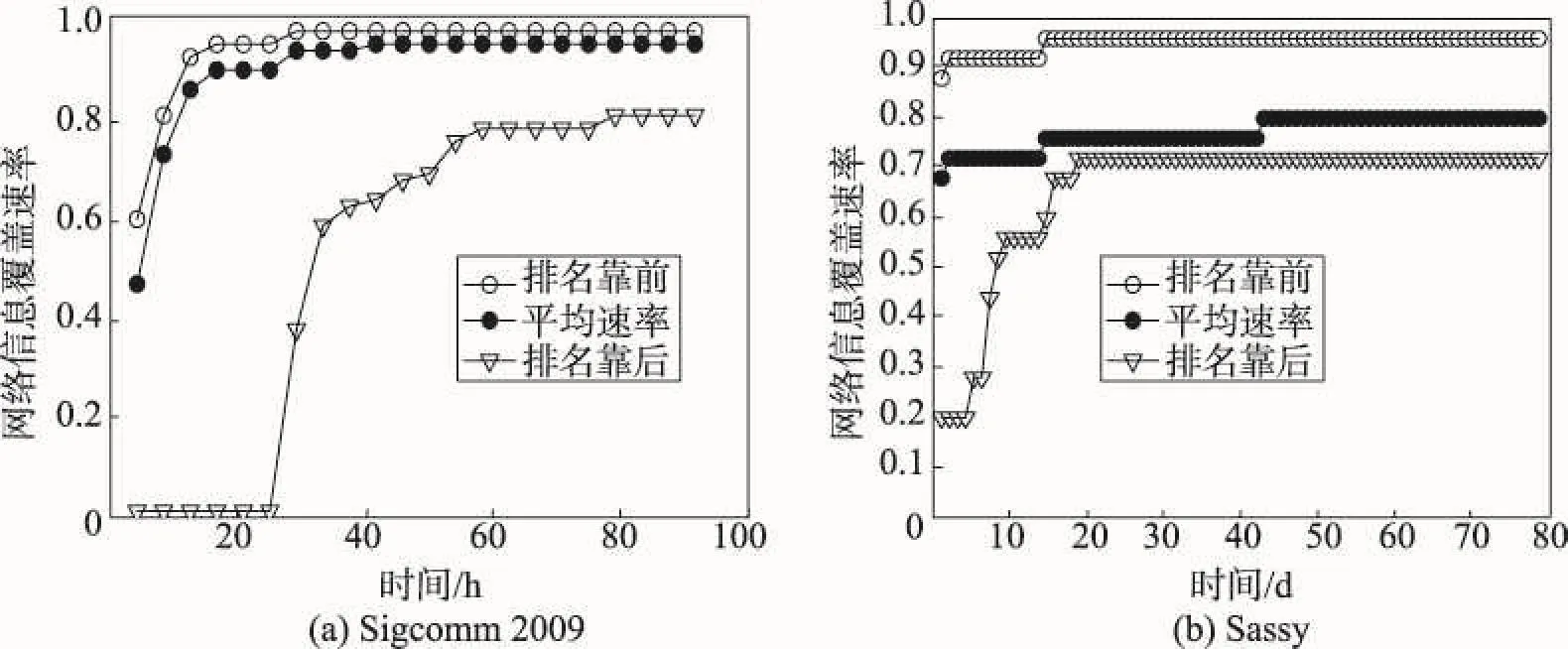
Fig.2 Comparison of message coverage图2 网络消息覆盖速率对比
4.3路径因子β对节点传播能力排名的影响
本实验针对路径因子β对节点关键程度排名的影响进行讨论。β用于对具有不同长度的动态通路进行衰减,使得“短动态通路对计算节点传播能力的贡献度较大,长动态通路对计算结果的贡献度较小”。在实际中,一方面可根据网络的动态程度,另一方面可根据需要传播的消息的具体特性,按照经验值设定β的具体取值。本实验中,针对各个数据集随机选取网络中的某一节点作为观测节点,考察β分别取(0.1,0.3,0.5)时,该节点在网络中关键程度的排名变化情况。如前文所述,时间间隔的选取问题仍是未有定论的问题。进行相关实验时,首先根据数据集的网络特性,按照已有研究[9]对时间间隔的设置方法,将Sigcomm的时间间隔设为4.08 h,Sassy的时间间隔设为1 d。另外本节将时间衰减因子取0,表示此实验暂不考虑时间因素,只考察路径因子β对节点传播能力排名的影响。本实验随机选择节点(Sigcomm中选中节点15,Sassy中选中节点5),应用本文方法计算节点的消息传播能力排名。实验结果如图3所示,横坐标表示各个快照的产生时间,纵坐标表示节点在该时刻的关键程度(消息传播能力)排名,随着β取值变小,节点关键程度排名变化更加剧烈,并最终趋于平稳。这是由于本文方法考虑了节点可产生的所有长度的动态通路,并且当β取值变大时,不同长度动态通路之间的贡献度差异会缩小,当β取值变小时,不同长度动态通路之间的贡献度差异会变大。当β取值变小时,节点关键程度的计算结果会受到较大的影响,最终导致节点关键程度排名变化较剧烈,并且当时间累积到一定程度时,节点的排名受历史相遇记录的影响而趋于平稳。
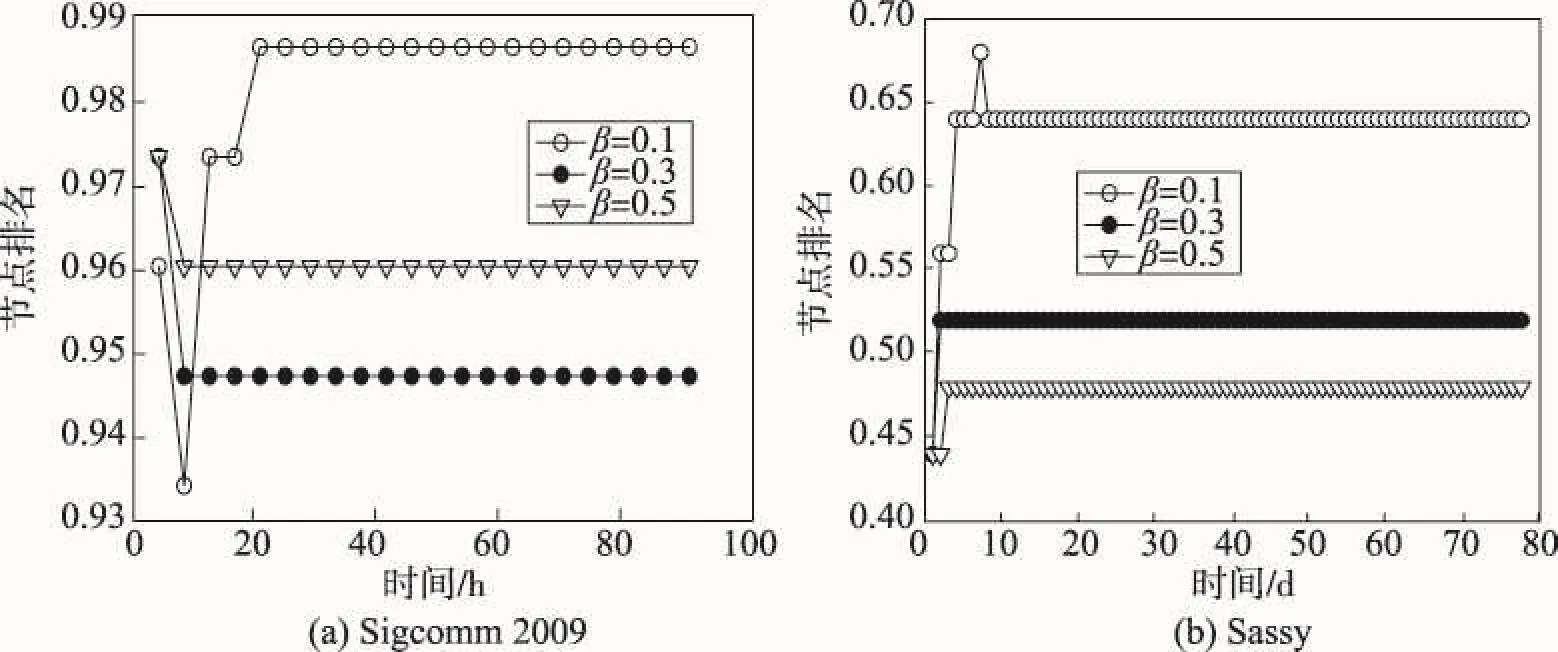
Fig.3 Impact on node rank of different β values图3 β对节点关键程度排名的影响
4.4时间因子α对节点传播能力排名的影响
本实验考察增加时间因素后,时间衰减因子α对节点关键程度排名的影响。为保持一致性,本实验利用前一实验针对各数据集随机选出的节点继续进行观测(Sigcomm中选中节点15,Sassy中选中节点5)。从之前实验的结果可以看出,当不考虑时间因素时,β取值较大,节点的排名变化较不明显。因此本实验中将β在各个数据集均设为0.5,α在每个数据集中分别取(0.1,0.5,1.0)观测节点关键程度排名的变化趋势。实验结果如图4所示,当α取值越大时,随着时间的推进,节点关键程度排名变化越剧烈。这是因为e-αΔtk可作为消息在tk时刻的重要性衡量因子,Δtk越小,说明该消息(影响)离现在时刻越近,重要程度越大,对计算结果的贡献度越大。Δtk越大,说明该消息(影响)离现在时刻越远,重要程度越小,对计算结果的贡献度越小。α取值大小直接影响衰减的快慢,α越大,衰减速率越快,节点关键程度变化越剧烈,最终导致节点关键程度排名变化越剧烈。与β考虑所有长度的动态通路不同,α考虑快照之间的“年龄差”集合{Δtk}的元素数目较少,这导致具有不同“年龄差”的消息的权重对计算结果都有较直接影响,若想突出具有某一“年龄差”的消息的贡献度,需要设置合适的时间因素衰减因子的取值。
4.5网络动态性对节点传播能力的影响
网络的动态性来源于节点间连边不断地建立与消失,导致网络的拓扑连通性不断变化,并对节点的影响力大小具有影响,更进一步,会影响节点在网络中的关键程度。直观上,当网络连通性较低时,节点的影响力普遍较小。最极端情况是网络中节点间不存在连边,此时节点的影响力为0;当网络连通性较强时,节点的影响力也会提升。最极端情况是网络为完全连通状态,节点到其他任意节点都存在长度为1的路径,节点的影响力此时达到最大值。本实验用于观测网络动态性影响节点关键程度排名的具体表现形式。为便于观测结果,引用前面实验的结论,在实验过程中将α和β均取0.5,用于降低计算结果的波动,从数据集中重新随机选择节点进行观测(Sigcomm中选中节点32,Sassy中选中节点12)。实验结果如图5所示,当该节点较活跃,与其相关的相遇记录总量快速增长时,节点的关键程度排名也会快速增长,当与其相关的相遇记录总量保持不变或增长较慢时,节点的关键程度排名也会相应降低,并且节点的关键程度排名的变化相对于网络的拓扑变化具有一定的滞后性。这是由于在当前快照中计算节点影响力时,其结果是由新产生的拓扑信息和所有的历史信息综合计算出来的,即新产生的拓扑信息一般不会直接决定最终的计算结果。因此当网络的拓扑变化积累到一定程度时,节点关键程度排名才会受到较明显的变化,即产生了图5所示的节点关键程度排名的滞后变化性。
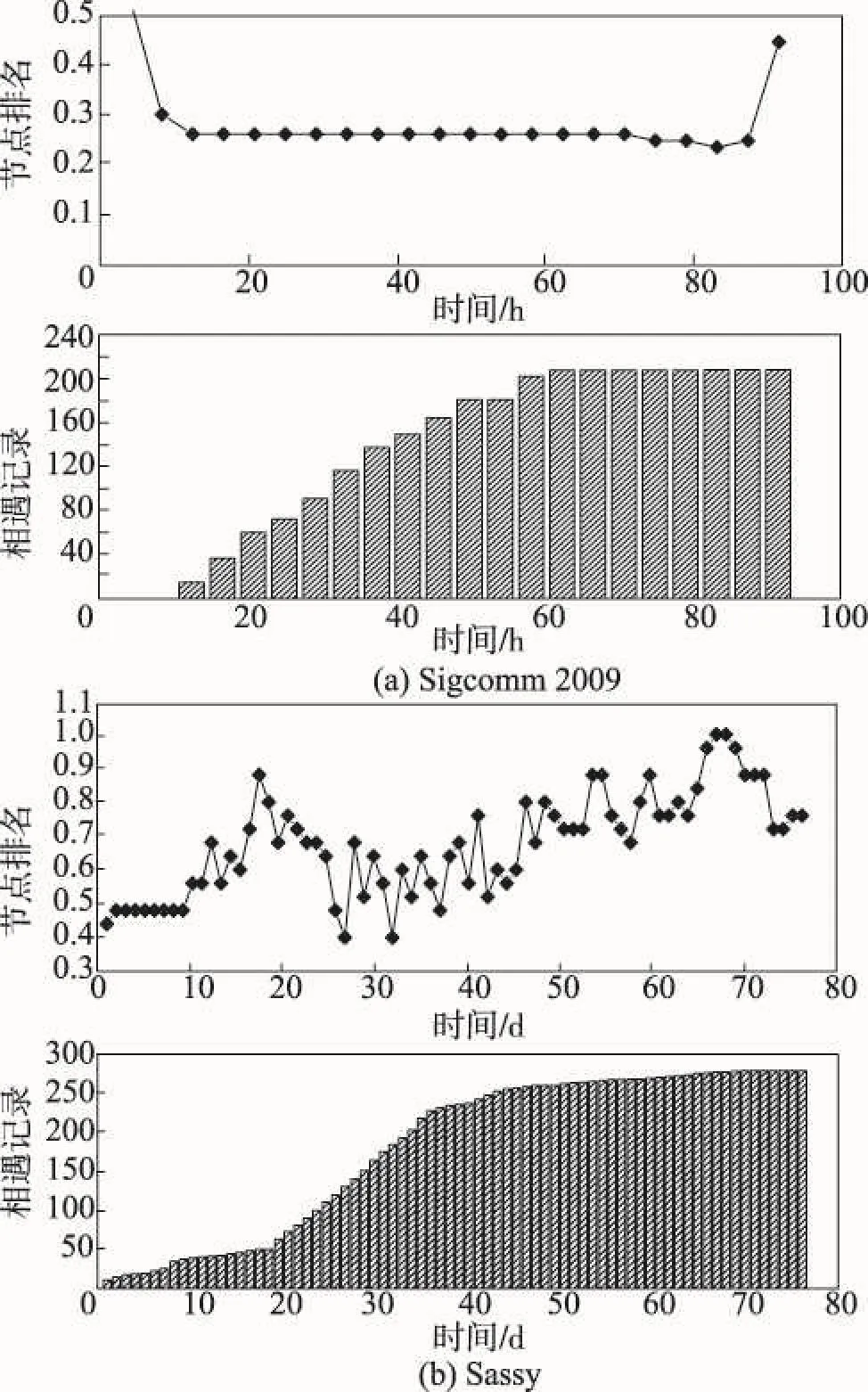
Fig.5 Contact density v.s. node rank图5 网络动态性对节点关键程度排名的影响
4.6预测节点的传播与获取消息的能力
式(5)的迭代形式使得本文方法可以基于当前快照的计算结果(历史信息)对后一快照中的节点传播或获取实时性消息的能力进行一定程度上的预测。而时间衰减因子α的不同取值即是对历史信息进行不同程度的处理——按照不同程度对历史相遇记录进行衰减。因此本节实验研究时间衰减因子α对预测精度的影响。本实验利用皮尔森相关系数作为预测结果的评判指标,计算出Qt+11与St+11,(Qt+1)T1与(St+1)T1的皮尔森相关系数,其中St+1是由式(2)计算出的在第t+1个快照中节点的影响力矩阵。皮尔森相关系数越大,说明利用本文方法预测出的结果越准确,相反,皮尔森相关系数越小,说明利用本文方法预测出的结果误差越大。根据具体的网络动态程度,按前面实验的结果设置路径因子β在两个数据集内均为0.5,考察时间因子α对预测准确性的影响。实验结果如图6所示,在Sigcomm数据集中当α取值为2.0与1.7时,本文方法的预测准确性分别达到最高值68%与65%。在Sassy数据集中当α取值为1.4时,本文方法的预测准确性达到最高值90%。
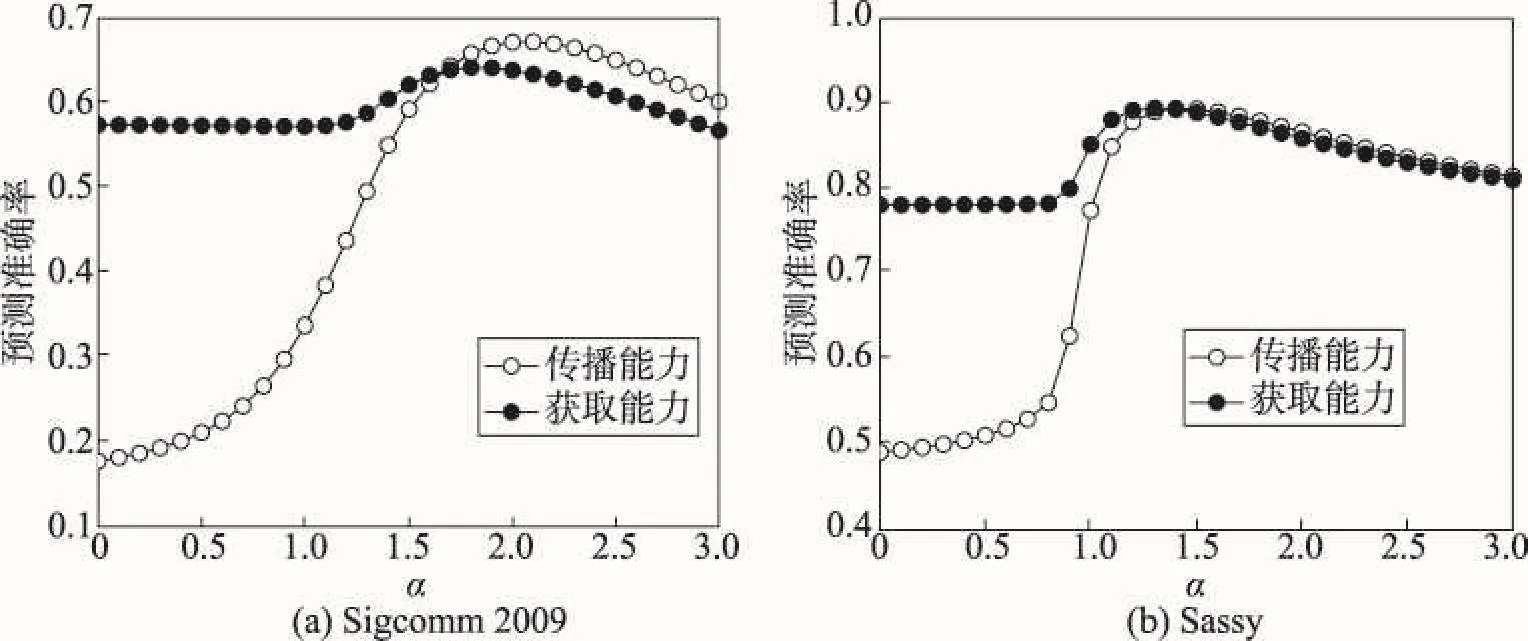
Fig.6 Impact of α on prediction accuracy图6 α对预测准确度的影响
4.7对衰减因子α与β的讨论
衰减因子α与β在本文方法中根据消息效用的不同衰减特性对动态通路进行衰减,且衰减因子α 与β均具有弹性,可根据网络状况以及研究目标对衰减因子的具体取值进行调节。β针对不同长度的动态通路进行衰减,主要考虑了节点间可产生相互影响或可相互传递消息的难易程度。α针对不同快照产生的动态通路进行衰减,主要考虑了节点之间产生影响的先后关系或节点之间传递消息的实时性。可根据网络的动态性程度或网络的研究(观测)目标设置这两个因子的具体取值。例如,若实验目的在于查看当网络所处的环境压力较大时节点传播实时消息关键程度的排名情况,可将α设为较大的数值,β设为较小的数值。这是因为网络所处环境压力大时,节点之间通信较困难,节点通过长通路进行消息传递的可能性很小,“旧消息”传递到当前快照的可能性也较小,即更看重短步长动态通路以及“较新消息”对结果的影响,通过设置α和β的取值,起到调节步长和时间因素的衰减速率的目的,最终可突出短步长动态通路以及“新消息”的作用。
5 结束语
本文针对移动P2P社交网络这类动态时变网络,提出了一种传播实时消息的关键节点发现方法。本文方法借助SNA方法将传统的复杂网络中基于静态网络的中心性指标分析方法扩展到时变动态网络中,将传统的通路概念延伸为动态通路概念。本文一方面参照静态物理学中的“格林函数”公式为不同长度的动态通路设置衰减因子,另一方面考虑拓扑演化的时向性及消息的实时性,设置时间衰减因子对不同“年龄”的消息进行不同程度的衰减,最终以迭代方式计算出动态通路的加权和,得到传播实时消息的关键节点评价函数。5组基于真实相遇数据的实验在验证本文方法正确性的同时,还表明了本文方法可在一定程度上对节点的消息传播与获取能力进行预测。
本文提出的传播实时消息的关键节点发现方法,虽然在理论和实验上均验证是正确有效的,但仍有以下缺陷需要继续完善:
(1)时间间隔的选取问题目前仍处在研究阶段,时间间隔不限于本文所利用的“相等时间间隔”划分形式,并且时间间隔选取的大小也会带来很多问题。例如时间间隔划分过大会使得快照内的相遇信息记录不完整;时间间隔划分过小会使得快照中存在过多的冗余相遇信息。本文按照数据的采集背景以及经验值设置时间间隔是一种无奈的折中策略,进一步针对时间间隔选取进行研究是有必要且是十分重要的。
(2)衰减因子的取值问题。本文按照研究目标以及网络状况设置衰减因子,并通过实验观测了衰减因子对结果的影响,认为衰减因子应当存在取值的上下界或是针对不同网络状态有最优选择,研究网络状况和衰减因子的取值关系是很有必要的。
(3)本文假设消息的生存期是无限大的,即不考虑节点会主动丢弃所携带消息的行为。不同网络状况下,消息生存期的设置方式不同,该项工作虽不与本文工作直接相关,但若考虑消息的生存期问题将有助于提升本文方法的普适性。
(4)选取合理的时间间隔以及运用合适的矩阵计算方法都会直接影响本文方法的复杂度。本文着重提出一种较新颖的在动态网络中发现关键传播节点的方法,故分析并进一步找到方法提升本文方法的算法效率是下一步的工作。
References:
[1] Spiliopoulou M. Evolution in social networks: a survey[M]// Social Network Data Analytics. Springer US, 2011: 149-175.
[2] Conti M, Giordano S, May M, et al. From opportunistic networks to opportunistic computing[J]. IEEE Communications Magazine, 2010, 48(9): 126-139.
[3] Chung K Y, Yoo J, Kim K J. Recent trends on mobile computing and future networks[J]. Personal and Ubiquitous Computing, 2014, 18(3): 489-491.
[4] Mota V F S, Cunha F D, Macedo D F, et al. Protocols, mobility models and tools in opportunistic networks: a survey[J]. Computer Communications, 2014, 48(8): 5519.
[5] Goyal E M, Chaudhary E M, Bharti E A. A survey of routing protocols for opportunistic mobile adhoc networks[J]. International Journal of Advanced Research in Computer Science, 2013, 4(9): 96-99.
[6] Ryan A R, Brian G, Jennifer N. Modeling dynamic behavior in large evolving graphs[C]//Proceedings of the 6th ACM International Conference on Web Search and Data Mining, Rome, Italy, Feb 4-8, 2013. New York, USA:ACM, 2013: 667-676.
[7] Katz L. A new index derived from social metric data analysis[J]. Psychometrical, 1953, 18(1): 39-43.
[8] Freeman L C. Centrality in social networks conceptual clarification[J]. Social Networks, 1979, 1(3): 215-239.
[9] Clauset A, Eagle N. Persistence and periodicity in a dynamic proximity network[C]//Proceedings of the DIMACS Workshop on Computational Methods for Dynamic Interaction Networks, 2007.
[10] Pirozmand P, Wu Guowei, Jedari B, et al. Human mobility in opportunistic networks: characteristics, models and prediction methods[J]. Journal of Network & Computer Applications, 2014, 42(3): 45-58.
[11] Wang Dashun, Pedreschi D, Song Chaoming, et al. Human mobility, social ties, and link prediction[C]//Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Diego, USA, Aug 21-24, 2011. New York, USA:ACM, 2011: 1100-1108.
[12] Chao Fan, Zhang Hongqi, Du Xuehui, et al. Improvement of structured P2P routing algorithm based on NN-CHORD [C]//Proceedings of the 7th International Conference on Wireless Communications, Networking and Mobile Computing, Wuhan, China, Sep 23-25, 2011. Piscataway, USA: IEEE, 2011: 1-5.
[13] Chandrasekaran V, Dantu R, Gupta N K, et al. Efficiency of social connection-based routing in P2P VoIP networks[C]// Proceedings of the 2nd International Conference on Communication Systems and Networks, Bangalore, Jan 5-9, 2010. Piscataway, USA: IEEE, 2010: 1-6.
[14] Newman M E J. Random graph as models of networks[M]// Handbook of Graphs and Networks: From the Genome to the Internet. [S.l.]: Wiley-VCH, 2005: 35-68.
[15] Rossi R A, Gallagher B, Neville J, et al. Modeling dynamic behavior in large evolving graphs[C]//Proceedings of the 6th ACM International Conference on Web Search and Data Mining, Rome, Italy, Feb 4-8, 2013. New York, USA: ACM, 2013: 667-676.
[16] Yoneki E, Hui P, Crowcroft J. Wireless epidemic spread in dynamic human networks, bio- inspired computing and communication[C]//LNCS 5151: Proceedings of the 1st Workshop on Bio- Inspired Design of Networks, Cambridge, UK, Apr 2-5, 2007. Berlin, Heidelberg: Springer, 2007: 116-132.
[17] Grindrod P, Parson M C, Higham D J, et al. Communicability across evolving networks[J]. Physical Review E, 2011, 83 (4): 046120.
[18] Grindrod P, Higham D J. A matrix iteration for dynamic network summaries[J]. SIAM Review, 2013, 55(1): 118-128.
[19] A community resource for archiving wireless data[EB/OL]. [2015-08-06]. http://crawdad.cs.dartmouth.edu/.
[20] Cai Qingsong, Niu Jianwei, Liu Mingzhu. Method for iden
tifying node dissemination capability in opportunistic social networks[J]. Journal of Software, 2012, 23(S1): 49-58.
附中文参考文献:
[20]蔡青松,牛建伟,刘明珠.一种评估机会社会网络中节点消息传播能力的方法[J].软件学报, 2012, 23(S1): 49-58.

BAI Yuqing was born in 1991. He is an M.S. candidate at School of Computer and Information Engineering, Beijing Technology and Business University, and the student member of CCF. His research interests include mobile computing and social computing, etc.白宇清(1991—),男,北京工商大学计算机与信息工程学院硕士研究生,CCF学生会员,主要研究领域为移动计算,社会计算等。

LI Haijian was born in 1974. He received the M.S. degree from Renmin University of China in 2010. Now he is a lecturer at College of Mathematics, Physics and Information Engineering, Langfang Teachers University. His research interests include computing application and data mining, etc.李海健(1974—),男,2010年于中国人民大学获得硕士学位,现为廊坊师范学院讲师,主要研究领域为计算机应用,数据挖掘等。

CAI Qingsong was born in 1973. He received the Ph.D. degree from Beijing University of Aeronautics and Astronautics in 2005. Now he is an associate professor at School of Computer and Information Engineering, Beijing Technology and Business University, and the member of CCF. His research interests include mobile ad-hoc networks, wireless sensor networks, DTN/opportunistic networking and mobile social networks, etc.蔡青松(1973—),男,2005年于北京航空航天大学获得博士学位,现为北京工商大学计算机与信息工程学院副教授,CCF会员,主要研究领域为移动自组网,无线传感器网络,DTN/机会网络,移动社会网络等。
Discovering Key Nodes in Mobile P2PSocial Networksƽ
BAI Yuqing1, LI Haijian2, CAI Qingsong1+
1. School of Computer and Information Engineering, Beijing Technology and Business University, Beijing 100048, China
2. College of Mathematics, Physics and Information Engineering, Langfang Teachers University, Langfang, Hebei 065000, China
+ Corresponding author: E-mail: caiqs@btbu.edu.cn
BAI Yuqing, LI Haijian, CAI Qingsong. Discovering key nodes in mobile P2P social networks. Journal of Frontiers of Computer Science and Technology, 2016, 10(3): 350-362.
Abstract:Conventional methods of finding key nodes in a network are mainly based on the theory of static graph, and cannot be applied to dynamic settings where connections between nodes appear and disappear dynamically. This paper focuses on a dynamic and evolving network, called mobile peer-to-peer social network (MPPSN), and proposes an efficient method on it to quantitatively identify the key nodes in the network. By extending the classical concept of centrality to the dynamic MPPSNs and using two elastic attenuation factors to characterize the walklength fading effect and the freshness of a time-bound message, this paper precisely derives an iterative matrix function to compute the relative importance of a node in MPPSN. Extensive experiments based on two real Trace datasets are conducted, and the results show that the analytical model is not only effective at identifying the most effec-book=351,ebook=55tive node in disseminating or receiving the latest useful messages but can even predict the node’s future behaviors as well as the network evolution at a very high accuracy.
Key words:mobile peer-to-peer social network; time-bound message dissemination; centrality analysis method; dynamic walk
doi:10.3778/j.issn.1673-9418.1509044
文献标志码:A
中图分类号:TP393

