变面积临界流文丘里喷嘴特性研究*
陈元杰, 葛 锐, 姚超玲, 严东旭, 沈文新
(1.浙江省计量科学研究院, 浙江 杭州 310000;2.浙江大学 海洋学院,浙江 杭州 310000)
变面积临界流文丘里喷嘴特性研究*
陈元杰1, 葛锐1, 姚超玲2, 严东旭2, 沈文新1
(1.浙江省计量科学研究院, 浙江 杭州 310000;2.浙江大学 海洋学院,浙江 杭州 310000)
摘要:针对目前气体流量计量领域临界流文丘里喷嘴临界流量不可调节或调节困难的情况,提出一种喉部过流面积可调节的变面积临界流喷嘴。通过结构分析、建模计算、流体力学Fluent仿真等方式,对棒状节流体、锥状节流体、台锥状节流体三种不同调节方式进行研究分析。结果表明:采用三种不同节流体的变面积临界流文丘里喷嘴均能实现临界流流量的调节,在背压比小于最大允许背压比后,流量保持一稳定值,基本不变。建模计算得到的理论值与Fluent仿真到的数据较为符合。
关键词:计量学; 临界流; 变面积; Fluent仿真; 文丘里喷嘴
0引言
临界流文丘里喷嘴作为流量计量装置中的核心部件,具有良好的稳定性,原理简单可靠。因此,其作为流量控制仪表或标准装置中的标准表而得到广泛应用。同时,其又作为量值传递标准器,在流量装置和流量仪表的量值传递,特别是在天然气计量工作中发挥着重要作用。
目前,临界流文丘里喷嘴主要存在问题是流量测量范围为“1”,即一个喷嘴只是一个流量,对流量的调节只能通过更换不同喉径的喷嘴或者多个喷嘴并联安装的方式实现[1],这在工业应用中往往较为困难,从而使其推广应用受到极大的限制。
本文通过研究、分析单个临界流文丘里喷嘴“多”流量调节的实现方法和可行性,设计一种喉部节流面积可调节的变面积临界流文丘里喷嘴,并通过数学建模和计算流体动力学(computational fluid dynamics,CFD)流体仿真对其特性进行研究,以期代替一系列不同喉部面积的临界流喷嘴的并联安装使用,从而大大提高量值传递和工业气体流量计量的效率成本。
1结构分析
1.1传统临界流文丘里喷嘴结构
传统临界流文丘里喷嘴结构如图1所示,其主要结构分为入口平面、入口收缩段、喉部、出口扩散段等几个部分[2]。
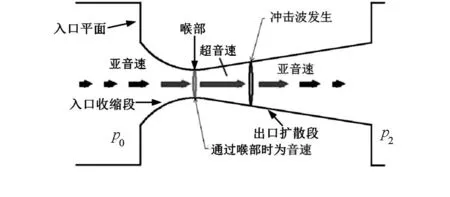
图1 传统临界流文丘里喷嘴结构原理图Fig 1 Principle diagram of structure of traditional critical flow Venturi nozzle
工作时,通过减小出口压力p2与入口滞止压力p0之比p2/p0(背压比),使其减小到某一数值时,喉部流速达到一固定值(为当地音速),当背压比再减小时,喉部流速不再改变,气体质量流量保持恒定,为临界流状态。临界流状态气体质量流量可由式(1)计算得到[3]
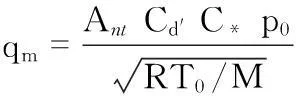
(1)
式中Ant为喉部过流面积;Cd′和C*为流出系数和临界流函数,可通过经验公式计算、查表、实测等方法得到,在一定温度和流体属性下为常数;p0为上游滞止压力;T0为上游滞止温度,R为气体常数,M为气体摩尔质量。因此,当气体属性、上游滞止条件(T0,p0不变)一定的情况下,流量qm值与过流面积Ant呈正比,而常规的临界流喷嘴喉部截面积为固定形式,无法进行调节。
1.2变面积临界流文丘里喷嘴结构
根据上述问题,本文设计了三种可行的变面积临界流文丘里喷嘴结构,通过在常规喷嘴喉部插入节流体的形式来调节喉部过流面积,从而实现喷嘴在临界流状态下流量调节。具体结构如图2~图4所示。
图2为棒状节流体结构,在常规喷嘴中插入一定直径的圆柱棒来实现。根据所需临界流流量的不同,更换不同直径的圆柱棒来实现流量的调节[4,5]。优点是结构简单,喷嘴内部流场相对于插入前变化不大;缺点是每次调节必须更换不同直径的圆柱棒,较为麻烦。但是相对于更换不同喉部直径的喷嘴来说,已经提高了效率,节约了成本。
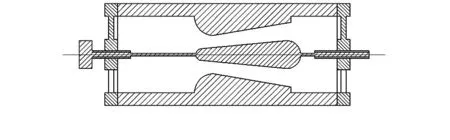
图3 文丘里喷嘴+锥状节流体Fig 3 Venturi nozzle with cone-shaped throttle body
图3为锥状节流体结构,在常规喷嘴中插入一圆锥体来实现。通过改变锥状节流体在喉部的位置来调节喉部过流面积的大小,从而实现临界流流量的调节。其优点是调节较为方便,并可进行连续调节;缺点是由于节流体是圆锥状,喷嘴内部流场变化较大,同时实际操作时外部驱动机构很难将圆锥体定位于同一位置,使其重复性较差。
图4为台锥状节流体结构,在常规喷嘴中插入具有一定台阶数的台锥体来实现。在结构上,其结合了棒状节流体和锥状节流体的特点,不仅调节方便,而且同一台阶插入到喉部时的临界流流量都相同,提高了其定位精度和重复性。其缺点是:流量调节为有极调节,可调流量数目和台阶数目相同。
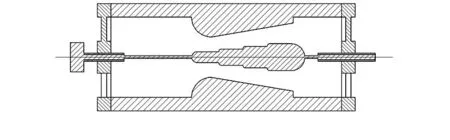
图4 文丘里喷嘴+台锥状节流体Fig 4 Venturi nozzle with hybrid-shaped throttle body
2建模与计算
变面积临界流文丘里喷嘴模型从结构上看,为在传统临界流文丘里喷嘴喉部插入一定结构的节流体,通过改变喉部过流面积来调节流量值。根据式(1)可得
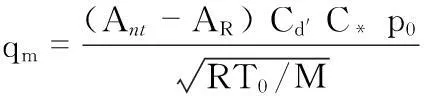
(2)
式中AR为节流体在喉部的截面积。建模计算时,取喷嘴喉部直径d=50mm,气流为干燥空气,其摩尔质量M=28.8g/mol,密度ρ=1.205kg/m3,大气压力p0=101 325Pa,温度T0=293.15K,气体常数R=8.314J/(mol·K)。临界流函数C*和流出系数Cd′根据查表得到,分别为0.685 131 3和0.98。以下结合式(2)和上述参数值,分别计算三种节流体对喷嘴临界流流量的调节。
2.1棒状节流体模型
该模型较为简单,建模时,插入喉部的圆棒半径为rr=8.8,16.1,21.0mm。结合上述参数,根据式(2)计算可得该模型的相应喉部过流面积和临界流流量,见表1。(选取合适的圆棒半径rr,使计算出来的体积流量接近常用流量,下同)。
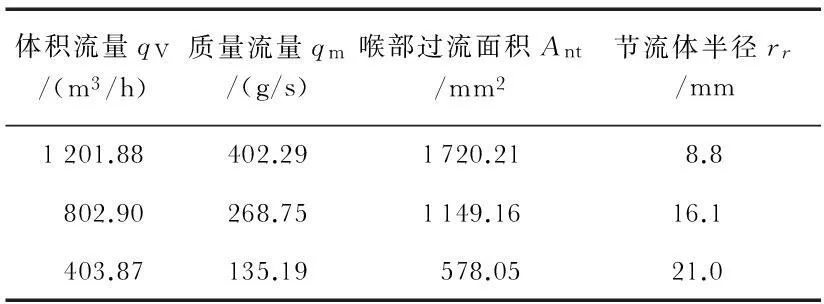
表1 文丘里喷嘴+棒状节流体计算参数
2.2锥状节流体模型
该模型的结构参数如图5所示。
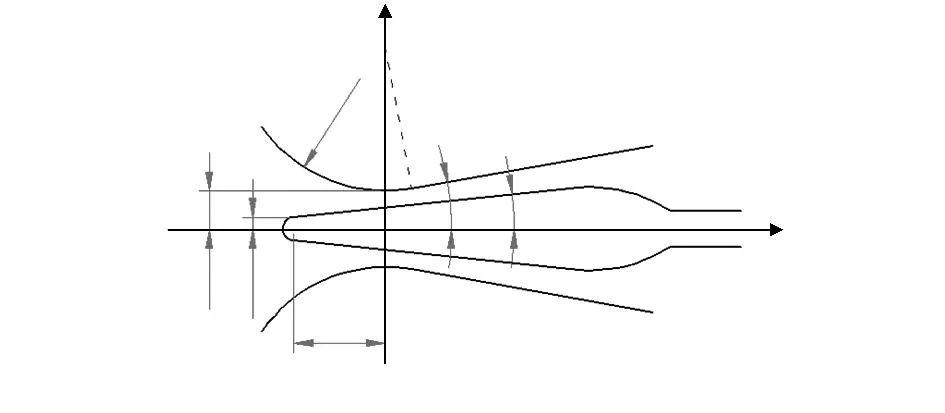
图5 锥状节流体模型结构参数(mm)Fig 5 Structure parameters of cone-shaped throttlebody model(mm)
图中,锥体半角为6°,头部半球半径为7.5 mm。喷嘴出口扩散段半角为10°,入口收缩段圆环面截面半径为100 mm。设喷嘴喉部位置为原点,节流体从右至左插入喉部距离为l。锥状节流体插入后,喷嘴喉部位置(过流面积最小处)发生改变,从原喉部位置向扩散段方向偏移一小段距离。由图5的几何关系,可得沿x轴各处过流面积为(x取值为0到入口收缩段圆弧与扩散段切点)
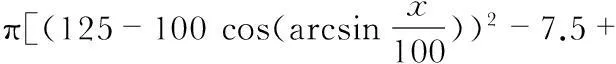
(3)
喉部面积S(x)最小的位置出现在dS/dx=0处,对式(3)求导可得
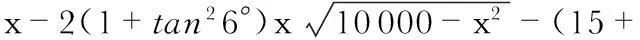
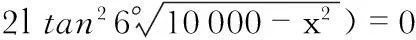
(4)
在确定节流体位置l后,可以根据式(4)获得喉部位置x0,代入式(3)后,可得新喉部过流面积S(x0)。
取l=10.6,49.4,78.5,102.8,124.1mm,经过式(2)~式(4)计算,可得出新喉部位置、喉部过流面积、临界流流量值等参数,如表2所示。
表2 文丘里喷嘴+圆锥状节流体计算参数
2.3台锥状节流体模型
该模型结构参数如图6所示。
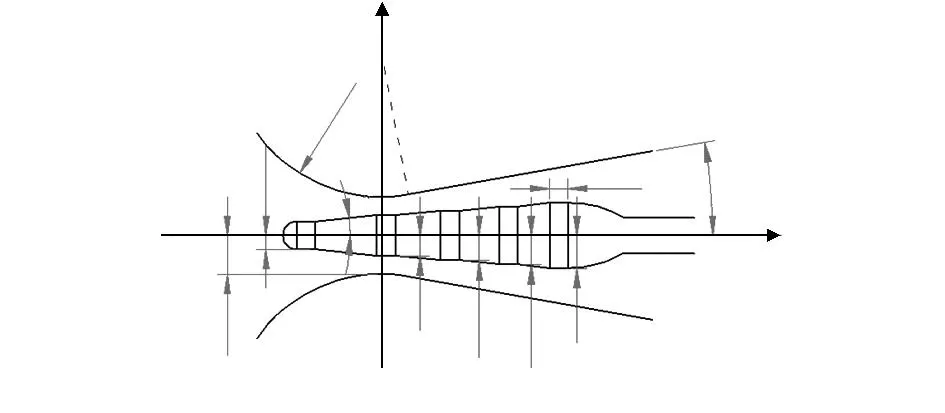
图6 台锥状节流体模型结构参数(mm)Fig 6 Structure parameters of hybrid-shapedthrottle body model(mm)
图中,各个台阶的半径为Rs,台阶长度为ls,台阶间用6°锥面过渡,其他尺寸与锥状节流体相同。由于节流体为台锥状,若台阶过短锥面过长,也会使过流面积最小的喉部向扩散段方向偏移,偏离原喉部位置。为保证最小过流面积在原喉部处,必须使台阶足够长。根据图6的结构,可得各个台阶后锥面处的过流面积为
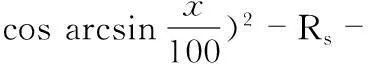
(5)
求导后为
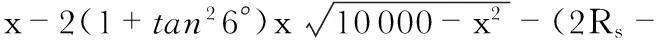
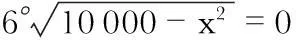
(6)
式中当x=ls时,能保证过流截面积在经过原喉部后,一直处于扩展状态,使最小过流面积保持在原喉部。将x=ls,Rs数值(Rs=8.8,13,16.1,18.8,21mm)依次代入式(7),可计算得到喉部不偏移的最小台阶长度ls=3.69,5.43,6.69,7.79,8.67mm。取最大值8.67mm(取整为9mm)作为台阶基础长度,在此基础上,再加3mm作为重复性定位误差,因此,台锥状节流体每个台阶的长度为12mm。
由于此时喉部不偏移,为原喉部位置,根据台阶半径Rs,喉部直径d值,经式(2)计算可得表3相应参数。
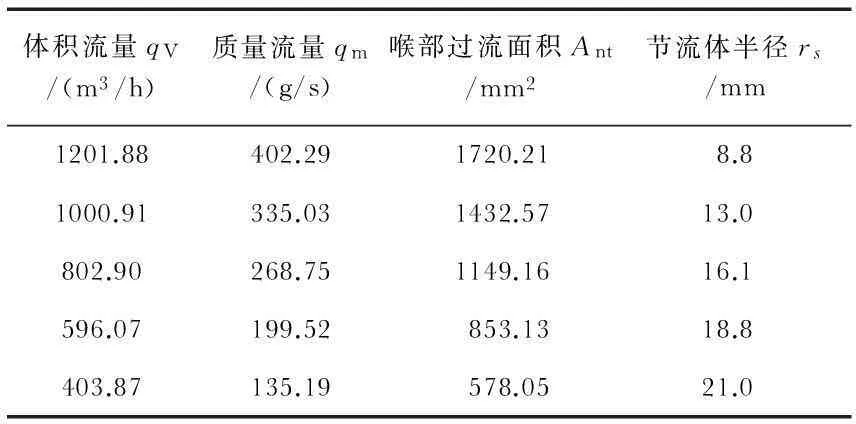
表3 文丘里喷嘴+台锥状节流体计算参数
3CFD仿真研究
本文采用FLUENT作为CFD分析工具,使用的网格模型采用ICEM CFD软件生成,仿真过程中选择压力基求解器,采用Spalart-Allmar湍流模型[6,7]。喷嘴入口平面上游设置长度、直径分别为5d(d为喷嘴喉部直径)的管道流场。入口边界条件设置为为一个大气压,出口压力根据临界背压比取多个点进行观测。
该仿真流场为严格对称的形状,为了提高仿真效率,将流场沿中轴线对称剖出1/4进行仿真,剖面设置为对称面[8]。限于篇幅,本文只对质量流量随背压比的变化特性进行仿真分析。以下仿真分析中,水平直线为理论流量值(其值可参考表1~表3中的qm),曲线为不同节流体在喉部不同位置时的仿真流量值。
3.1棒状节流体仿真分析
将半径为r=8.8,16.1,21 mm三种圆柱棒插入到常规喷嘴中进行仿真,背压比在0.9~0.5间变化,仿真结果如图7。
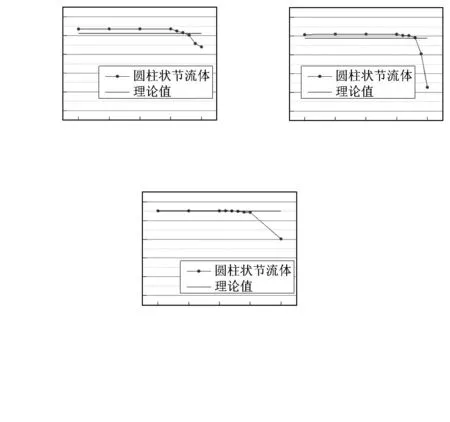
图7 棒状节流体模型流量—背压比曲线图Fig 7 Curve of flow as a function of back pressure ratio of rod-like throttle bady model
从图中可以看出:流体在背压比不断减小的过程中,达到了临界流体状态,其最大允许背压比在0.8~0.9之间(1和2约为0.8,3约为0.76)。此时,背压比再减小,质量流量基本不变。
3.2锥状节流体仿真分析
根据图5的结构,将圆锥体插入喷嘴喉部不同深度进行仿真,分别为l=10.6,49.4,78.5,102.8,124.1 mm,并在不同的背压比下,观察其流量变化。仿真结果与理论计算结果对比如图8所示。
从图中可以看出:各个插入位置的气体流量均能达到临界流状态,其最大允许背压比在1,2,3位置约为0.84,第4个位置约为0.8,第5个位置约为0.76。此后,随着背压比的减小,流量值基本不变。
3.3台锥状节流体仿真分析
根据图6的结构,将半径r=8.8,13,16.1,18.8,21 mm的台阶依次插入喷嘴喉部,并在不同背压比下,观察其流量变化。仿真结果与理论计算结果对比如图9所示。
从图中可以看出:各个台阶位置的气体流量均能达到临界流状态,其最大允许背压比在1,2,3位置约为0.85,第4个位置约为0.80,第5个位置约为0.74。此后,随着背压比的减小,质量流量值基本不变。
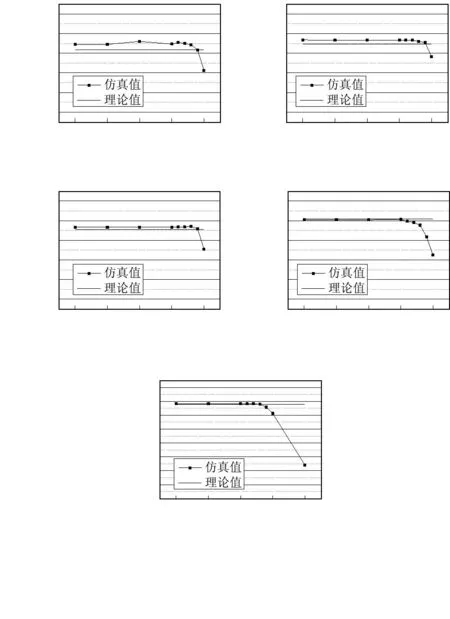
图8 锥状节流体模型流量—背压比曲线图Fig 8 Curve of flow vs back pressure ratio of cone-shaped throttle body model
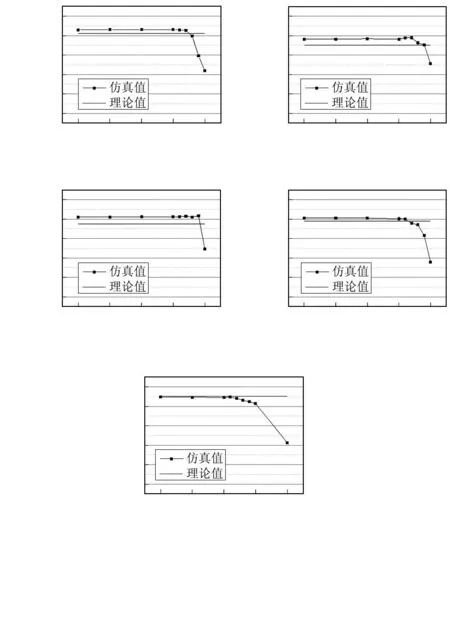
图9 台锥状节流体模型流量—背压比曲线图Fig 9 Curve of flow vs back pressure ratio of hybrid-shapedthrottle body model
3.4现象分析
将气体临界流状态下质量流量仿真值与理论计算值进行比较可知,两者的大小基本一致,但随着过流面积的增加(插入喉部的节流体直径变小),误差有所增加。分析其原因,可能是在进行理论计算时采用的流出系数Cd′不够准确。本文为计算方便,Cd′值统一为0.98,而实际上,该值随着喉部雷诺数Re增大而增大,而Re会随着过流面积的增加而增大。因此,随着过流面积的增加,实际理论计算值应更大一些。Cd′与Re对应关系如表4所示。
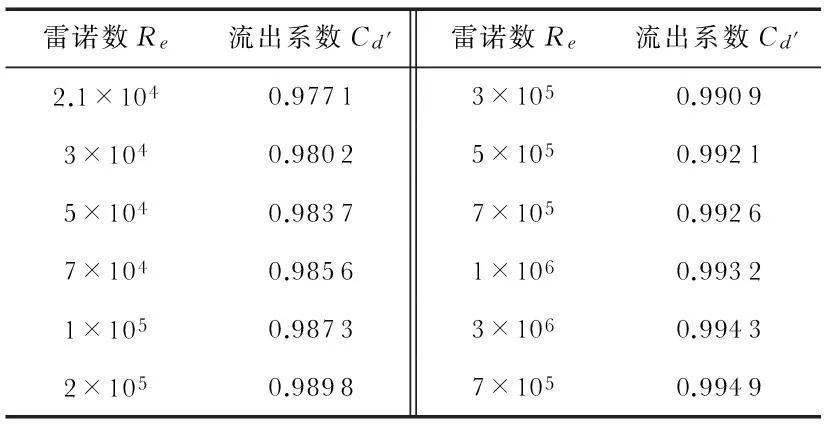
表4 流出系数与喉部雷诺数对应关系
4结论
本文通过建模分析计算、CFD仿真的相互印证可知,变面积临界流文丘里喷嘴在背压比小于最大允许背压比时,其流场能够达到临界流状态。棒状节流体流场简单稳定,理论计算方便,但更换较为麻烦;锥状节流体调节方便,其最小喉部位置较原喉部位置有所偏移,但重复性较差;台锥状节流体结合了棒状节流体和锥状节流体的特点,不但调节方便,而且具有较好的重复性。仿真虽与理论计算有一定误差,但是通过查表对Cd′值的修正,或通过PVTt等设备的实流标定,得到准确的Cd′,能进一步提高计量的准确性。
参考文献:
[1]ISO/TC 30/SC 2.ISO 9300—2005.Measurement of gas flow by means of critical flow Venturi nozzles[S].
[2]GB/T 21188—2007.用临界流文丘里喷嘴测量气体流量[S].
[3]梁国伟,周宁宁,李长武.临界流文丘里喷嘴流量计的原理与应用[J].中国计量学院学报,2004,15(3):186-190.
[4]Kim J H,Kim H D,Park K A.Computational/experimental study of a variable critical nozzle flow[J].Flow Measurement and Instrumentation,2006,17:81-86.
[5]Kim H D,Kim J H,Park K A,et al.Computational study of the gas flow through a critical nozzle [J].Journal of Mechanical Engineering Science,2003,217(10): 1179-1189.
[6]王福军.计算流体动力学分析—CFD软件原理与应用[M].北京:清华大学出版社,2004:85-88.
[7]胡坤,李振北.ANSYS ICEM CFD工程实例详解[M].北京:人民邮电出版社,2014:55-60.
[8]王丽辰,朱云,郑哈,等.基于 Fluent的临界流文丘里喷嘴的内部流场仿真分析[J].科学技术与工程,2013,13(34):10392-10396.
Research on characteristics of variable area critical flow Venturi nozzle*
CHEN Yuan-jie1, GE Rui1, YAO Chao-ling2, YAN Dong-xu2, SHEN Wen-xin1
(1.Zhejiang Institute of Metrology,Hangzhou 310000,China;2.Ocean College,Zhejiang University,Hangzhou 310000,China)
Abstract:In order to regulate critical flow rate of traditional critical flow Venturi nozzles,a new variable throat-area critical flow Venturi nozzle is proposed,throat area of which can be adjusted.Three different adjusting methods,including rod-style method,cone-style method and hybrid-style method,are analyzed by means of structure analysis,modeling calculation and fluid dynamics Fluent simulation.Results show that the critical flow of the new variable critical flow Venturi nozzles can be regulated well by using three different methods and when back-pressure ratio is smaller than the maximum allowable back pressure ratio,the flow rate of the new nozzle is almost kept constant,though the back-pressure ratio is still descending.And Fluent results coincides with the theoretical value calculated by modeling.
Key words:metrology; critical flow; variable area; Fluent simulation; Venturi nozzle
DOI:10.13873/J.1000—9787(2016)03—0044—05
收稿日期:2015—06—04
*基金项目:国家质检总局一般项目(2013QK060)
中图分类号:TH 814
文献标识码:A
文章编号:1000—9787(2016)03—0044—05
作者简介:
陈元杰(1984-),男,浙江慈溪人,硕士,工程师,主要从事气体流量计性能研究。

