试射法求解二维层流边界层中的Falkner-Skan方程

王　诚，周　振，石少卿，陈　暲

(中国人民解放军后勤工程学院　a.军事土木工程系；b.国家救灾应急装备工程技术研究中心； c.国防建筑规划与环境工程系，重庆　401311)



试射法求解二维层流边界层中的Falkner-Skan方程

王诚a，周振b，石少卿a，陈暲c

(中国人民解放军后勤工程学院a.军事土木工程系；b.国家救灾应急装备工程技术研究中心； c.国防建筑规划与环境工程系，重庆401311)

摘要：研究了不可压缩的粘性流体绕流楔形物体的Falkner-Skan方程，通过Matlab程序采用试射法求出了Falkner-Skan方程的数值解，说明试射法是求解Falkner-Skan方程的一种有效解法。

关键词：Falkner-Skan方程；试射法；数值解

流体力学中常常会遇到微分方程组的求解问题，虽然部分特殊的方程组可通过解析法求解，但大部分微分方程组主要借助于数值法求解。常见的数值解法主要有龙格-库塔法、蒙特卡洛法、吉尔法等[1]。

试射法可用于偏微分方程组的求解，其原理是将边值问题转换为初值问题求解：通过对方程初略的分析，先取定一个初值；再联合原方程组中的边界条件作为初值条件，逐步推进求解；求解至另一个已知边界条件时，比较两者间的差异，决定是否结束计算或修正初值重复求解[1-4]。

1Falkner-Skan方程

不可压缩流体二维定常流动的边界层方程为

当

即

ue=Cx1-2α=Cxm

采用流函数的形式，边界层方程化为

式中：β是压力梯度；β>0为顺压梯度；β<0为逆压梯度。

Falkner-Skan方程是V．M．Falkner和S．W．Skan于1931年首先提出，由相似变换将二维二阶偏微分方程转化为一个一维三阶常微分方程，是描述不可压缩的黏性流体绕流楔形物体的方程[5-8]。

2基于Matlab的试射法求解

2.1求解思路

基于Matlab采用试射法求解，流程如图1所示。

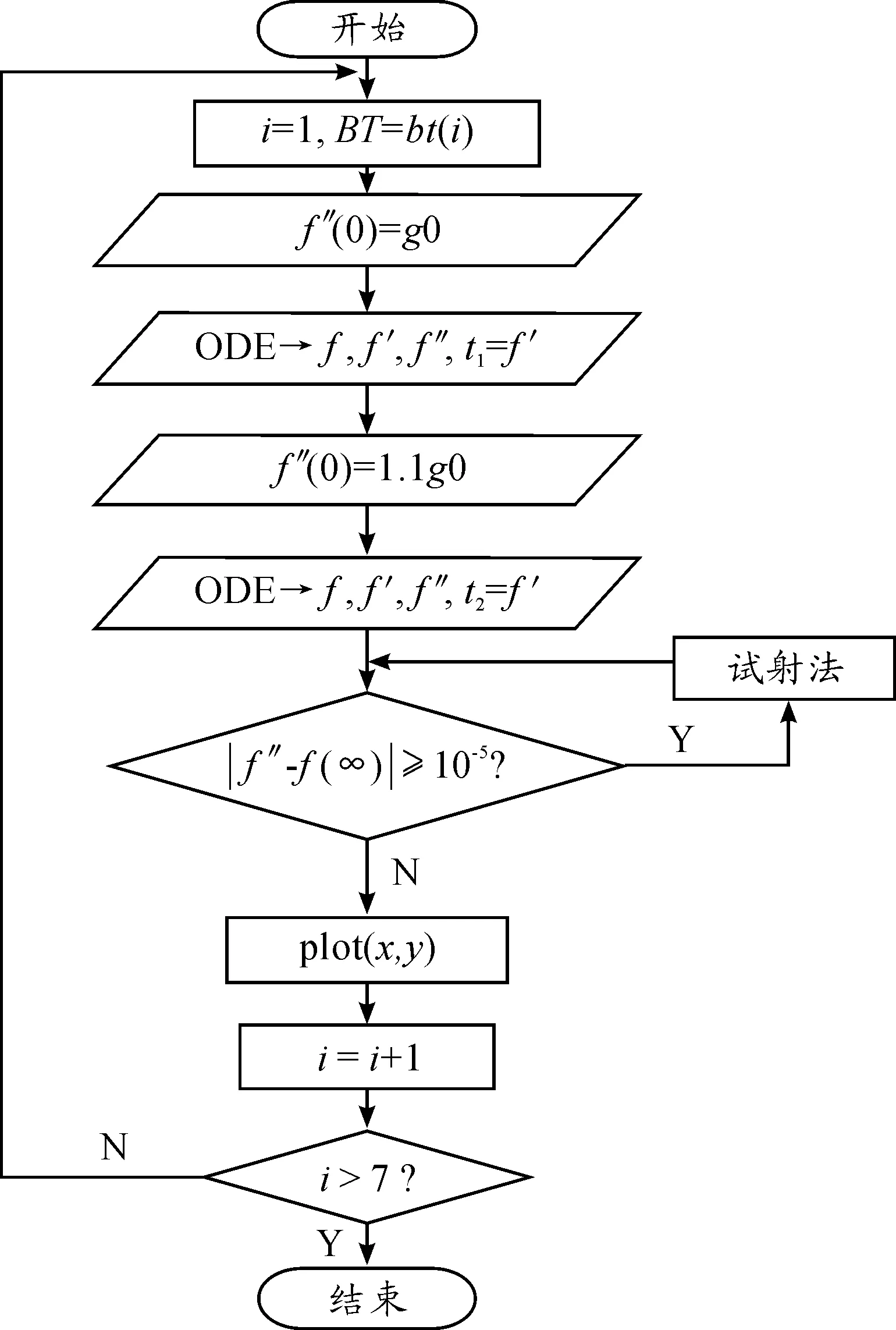
图1　求解Falkner-Skan方程数值解流程

1) 用Matlab中求常微分方程数值解的函数ode45求解。将方程改写为ode45的标准格式。令y(1)=f, y(2)=f ′, y(3)=f ″，原方程转化为：

边界条件为：

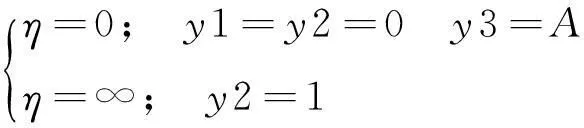
但此时没有初值f ″(0)，不符合ode45函数的计算条件，所以应当将其求出。

2) 先假定一个，如f ″(0)=0.5，则利用试射法，通过循环语句求解方程。当求出f ′的数值与f ′(∞)=1的差值小于给定精度时(本文的给定精度为10-5)，循环停止。

4) 最后绘出图像。

2.2Matlab求解程序

M文件(hanshu.m)

function dy=hanshu(x,y)

dy=zeros(3,1);

dy(1)=y(2);

dy(2)=y(3);

dy(3)=-(0)*(1-(y(2))^2)-y(1)*y(3);

end

主程序(main.m)

clc;

clear all;

close all;

global BT;

bt=[0,1/10,1/8,1/6,1/4,1/2,1];%β依次为0,1/10,1/8,1/6,1/4,1/2,1

jiashe=0.99;%假设f ″(0)的初值为0.99

mubiao=1;%f ′(∞)=1为目标值

for i=1:7 %β循环7次

BT=bt(i);

g0=jiashe;

y0=[0,0,g0];

[x,y]=ode45(′hanshu′,[0:0.03:5.5],y0); %Matlab自带解常微分方程的函数

t1=y(end,2);%取矩阵最后一行第二个元素值f ′

g1=1.1*g0; %更新f ″(0)

y0=[0,0,g1];

[x,y]=ode45(′hanshu′,[0:0.03:5.5],y0);

t2=y(end,2);

while abs(t2-mubiao)>=10^(-5)%比较f ″与f ′(∞)=1

g=g1+(g1-g0)*(mubiao-t2)/(t2-t1);%试射法修正f ″(0)

t1=t2;

y0=[0,0,g];

[x,y]=ode45(′hanshu′,[0:0.03:5.5],y0);

t2=y(end,2);

g0=g1;

g1=g;

end

3求解结果

运行程序，求得数值解，绘出的曲线如图2所示。由图2(b)的f′(η)曲线可以看出：在顺压梯度下，边界层逐渐变薄，这与以往的结论一致[3]。

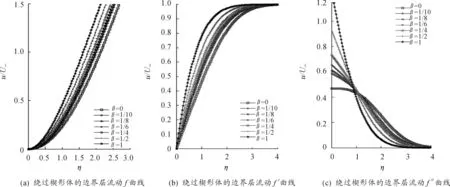
图2　Falkner-Skan方程数值解曲线

4结束语

本文利用Matlab编程，采用试射法计算求解了二维层流边界层中的Falkner-Skan方程，结果表明:试射法是求解Falkner-Skan方程的一种有效方法。

参考文献：

[1]范荫恒,刘晓明,刘丹竹.试射法解二阶线性常微分方程模拟反应动力学过程[J].实验技术与管理,2007,24(11):46-48.

[2]帕力旦·赛力提尼亚孜,张知难.试射法在求解二阶线性微分方程边值问题中的应用[J].新疆大学学报(自然科学版),2006,23(1):39-43.

[3]徐静,邓光.非线性一般两点边值问题的试射法[J].内江科技,2006(8):77.

[4]徐自新.微分方程近似解[M].上海：华东化工学院出版社，1990.

[5]郑连存,温安国,张欣欣.Falkner-Skan方程的近似解析解[J].计算力学学报,2008(4):506-510.

[6]杨建超,康宏春.Falkner-Skan方程的某些新结果[J].成都信息工程学院学报,2009(6):608-610.

[7]李林汉,姜伟.基于同伦分析的Falkner-Skan方程近似解[J].廊坊师范学院学报(自然科学版),2013(1):11-14.

[8]罗敏,胡建成.边界层理论中Falkner-Skan方程的数值解[J].四川大学学报(自然科学版),2012,49(3):514-516.

(责任编辑刘舸)

Application of Liner Shooting Method for Falkner-Skan Equation in Two-Dimension Boundary Layer

WANG Chenga, ZHOU Zhenb, SHI Shao-qinga, CHEN Zhangc

(a.Department of Civil Engineering; b.Engineering and Technological Research Center of National Disaster Relief Equipment;c.Department of National Defense Architecture Planning & Environmental Engineering, Logistical Engineering University, Chongqing 401311, China)

Abstract:The Falkner-Skan equation for incompressible viscous fluids flowing around wedge was introduced. By using the Matlab and liner shooting method, numerical solutions were done. It shows that liner shooting method is an effective way to solve the Falkner-Skan equation.

Key words:Falkner-Skan equation; liner shooting method; numerical solution

收稿日期：2015-12-26

基金项目：国家自然科学基金资助项目(51378495)

作者简介：王诚(1991—)，男，硕士研究生，主要从事防灾减灾工程研究。

doi:10.3969/j.issn.1674-8425(z).2016.05.010

中图分类号：O643.1

文献标识码：A

文章编号：1674-8425(2016)05-0053-04

引用格式：王诚，周振，石少卿，等.试射法求解二维层流边界层中的Falkner-Skan方程[J].重庆理工大学学报(自然科学)，2016(5):53-56.

Citation format：WANG Cheng, ZHOU Zhen, SHI Shao-qing,et al.Application of Liner Shooting Method for Falkner-Skan Equation in Two-Dimension Boundary Layer[J].Journal of Chongqing University of Technology(Natural Science)，2016(5):53-56.