MMC-HVDC数模混合仿真功率接口算法研究
林楚乔,江守其,陈厚合
(东北电力大学 电气工程学院,吉林 吉林 132012)
MMC-HVDC数模混合仿真功率接口算法研究
林楚乔,江守其,陈厚合
(东北电力大学 电气工程学院,吉林 吉林 132012)
摘要:功率连接型数模混合仿真结合了物理模拟仿真和实时数字仿真的优点,成为复杂电力系统研究分析的关键手段,功率接口算法是其关键技术。为此,提出一种适用于模块化多电平换流器高压直流输电系统数模混合仿真的功率接口算法。利用Routh稳定判据得出功率接口稳定运行的必要条件,提出换流变置于物理侧,同时引入反馈电流滤波器提高系统的稳定性。在PSCAD/EMTDC中构建基于理想变压器法的双端高压直流输电数模混合仿真系统,验证了该接口算法的稳定性和精确性。
关键词:模块化多电平换流器;数模混合仿真;理想变压器法;接口稳定性
柔性直流输电技术因其各方面的优点快速发展,其换流器含有大规模的电力电子器件,导致交直流混合系统动态行为复杂[1-3],为了对这种复杂的交直流混合系统进行分析研究,需采用有效的仿真手段对其开展多方面地深入研究。
功率连接型数模混合仿真,又称功率硬件在环(Power Hardware-In-The-Loop,PHIL)仿真,结合了实时数字仿真和物理模拟仿真的优点[4],既可以准确模拟MMC 换流阀动态特性以及交直流互联电网暂态特性,还可以对大型交直流混联电网规划设计方案、对数字仿真技术无法实现的课题开展仿真实验研究。PHIL仿真是MMC-HVDC仿真实验研究的有效手段。
PHIL仿真系统需要实现数字侧与物理侧实际功率的传输和实时信号的交互,其功率接口单元包含信号采集变换器、大容量功率变换器等装置,由其引入的噪声和时间延迟将影响PHIL闭环仿真系统的稳定性和精确性[5]。通过选取合适的接口算法,可以有效地提高PHIL仿真系统的仿真特性,因此对功率接口算法的研究成为PHIL研究中的关键问题[6]。很多学者对其进行了大量研究。文献[7,8]分析了在阻抗匹配特殊条件成立下的阻尼阻抗接口算法系统的稳定性和精确性,对比了理想变压器算法和阻尼阻抗算法在不同条件下的优缺点。文献[9-11]采用基于行波理论输电线贝杰龙模型的功率接口技术实现了数模混合仿真,该算法需要实时采集两侧电压源和电流源的历史数据,缺点是需要在物理侧增加电阻,电阻参数与线路有关,实现不够灵活。
本文提出了改进的理想变压器模型(Ideal Transformer Model,ITM)法。在研究MMC运行机理的基础上,建立了戴维南等效模型,并运用Routh判据推导出接口算法的稳定条件,通过引入反馈电流滤波器有效提高了接口稳定性。采用戴维南等效方法建立MMC模型,构建基于改进ITM的双端高压直流输电数模混合仿真系统,对其稳定性和精确性进行研究分析;通过对接口算法改进,使混合仿真系统具有更好的稳定性和精确性。
1MMC-HVDC数模混合仿真系统结构
PHIL系统主要由实时数字仿真系统建立的虚拟电力系统(Virtual Electrical System,VES),实际物理被测试系统(hardware under test,HUT)和功率接口3个子系统组成,其结构如图1所示。
VES子系统运行于实时数字仿真器。在仿真运行过程中,数字仿真器在每个仿真步长内需要完成外部信号的采集,模型的实时求解以及对物理侧换流器进行激励等任务。HUT子系统是指被测试的换流变、MMC等物理装置。
功率放大器一般采用大功率电压源变换器,本文分析时将其抽象成受控电压源与延迟环节的组合[12-14]。电流互感器、电压互感器采集HUT侧的电压与电流后,反馈到实时数字仿真系统中,以实现下一仿真步长的求解。接口算法主要实现DSS和PSS交换信号的处理,运行于DSS子系统中。ITM算法具有较好的精确性、实施简便等优势,成为各领域数模混合仿真应用最为广泛的接口算法。
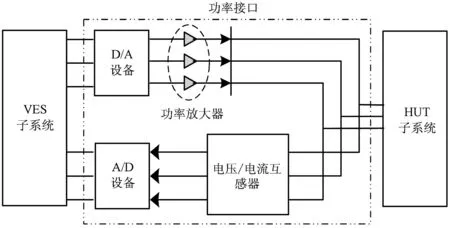
图1 PHIL仿真系统结构
2理想变压器法及其改进算法
2.1ITM特性分析
理想变压器模型算法是实现PHIL仿真功率连接最原始和最易实现的方法[15],被广泛应用于实践中。根据被放大信号的类型,可将其分为电流型ITM和电压型ITM,具体结构如图2所示。

图2 ITM接口结构原理图
ITM算法是以电路中的替代定理为理论依据,以常用的电压型ITM为例,其数字侧采用受控电流源来等效模拟物理侧电路,控制电流是由实际物理侧电流互感器的测量电流经A/D转换后得到的;物理侧则采用受控电压源来等效模拟数字侧电路,其控制电压是数字侧电压经D/A转换和功率放大器放大后的结果。在考虑各环节总延时的情况下,可得ITM算法的等效开环传递函数为:

(1)

(2)
式(1)、(2)分别为电压型ITM和电流型ITM的开环传递函数,ZS和ZH分别为数字侧和物理侧的等效阻抗。
以电压型ITM为例,设其ZS=sL1+R1,ZH=sL2+R2,根据式(1)可得其特征方程式为1+GOL_V=0,即:

(3)


(4)
可将特征方程式改写为:
(L2-L1)s2k+(kR2-kR1+L1+L2)s+(R1+R2)=0 .
(5)
根据Routh判据可得其接口稳定条件为:

(6)
由于系统总延时通常很小,即k值很大,因此接口稳定性主要取决于L2与L1的大小。当实际物理侧等效电感小于数字侧等效电感时,接口系统将不稳定,致使其稳定性较差,限制了ITM接口算法的应用效果。针对MMC-HVDC数字物理混合仿真系统,由于其物理侧等效阻抗不是恒定值,这将严重影响ITM接口算法的稳定性,对其进行改进,以保证系统的安全稳定运行。
2.2改进ITM算法
针对ITM接口算法稳定性取决于VES与HUT等效电感大小关系问题,提出将换流变压器放置在物理侧,以此增大HUT的等效电感,提高ITM的稳定性,并在此基础上引入反馈电流滤波器,以提高接口稳定性。改进算法的具体实现方法如下。
在电流反馈回路引入低通滤波器,其传递函数为:

(7)
可得改进ITM算法的特征方程式为:
s3kL2+(αkL2+kR2+L2-αkL1)s2+(αkR2+αL2+R2-αkR1+αL1)+α(R2+R1)=0 ,
(8)
从式(8)可以得到,引入反馈电流滤波器改变了功率接口的稳定条件,由于α可以影响低通滤波器的截止频率以及特征方程的闭环极点,因此可通过选取适当α值,以保证接口系统的稳定运行。
3改进ITM算法的仿真验证
为了验证所提出的改进ITM算法的有效性,在PSCAD/EMTDC电磁暂态仿真软件中搭建了双端背靠背11电平MMC-HVDC仿真系统,如图3所示,其中MMC子模块采用戴维南等效模型,通过Fortran语言编写自定义函数来实现。MMC1采用定直流电压和定无功功率控制,MMC2采用定有功功率和定无功功率控制,仿真步长为20 μs,系统参数如表1所示。
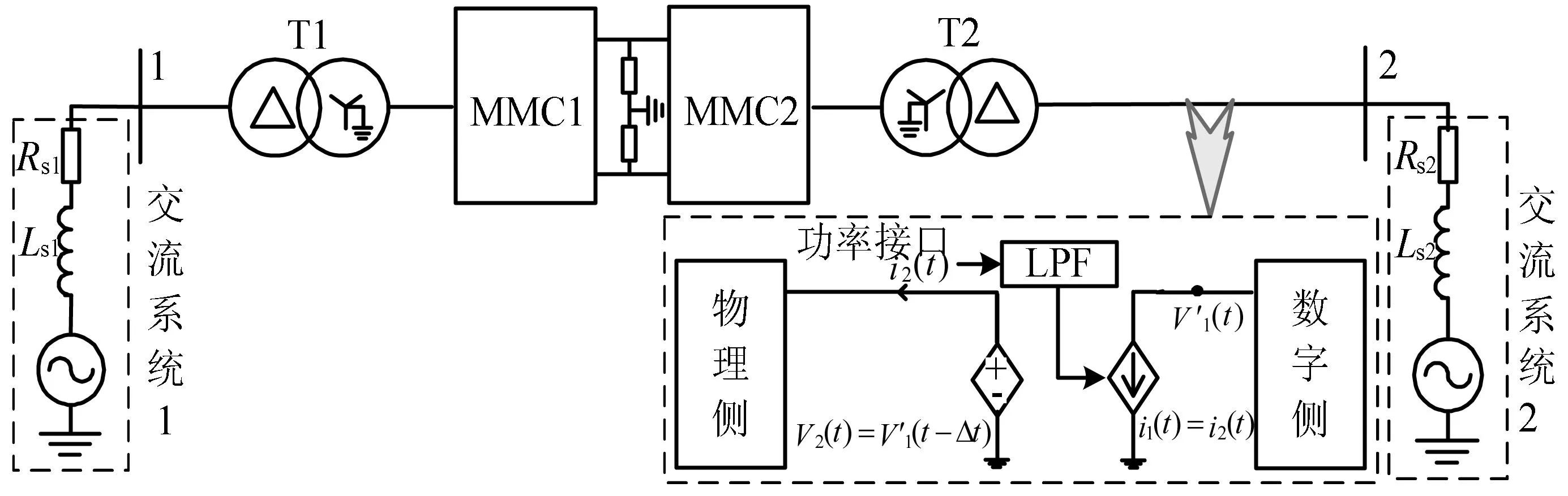
图3 MMC-HVDC测试系统示意图

部件参数数值交流系统交流电压UL-L_RMS/kV35等效电阻Rs/Ω0.1等效电感Ls/H0.08变压器接线形式Δ/YN额定容量STN/MVA30变比K/(kV/kV)35/31等值电阻RT/Ω0.01等值电感LT/H0.01MMC桥臂电感L0/H0.053子模块电容C/uF6000电容初始电压UC0/kV6直流系统直流电压Udc/kV60额定传输容量SN/MVA20功率接口D/A及功放延时tp/us40A/D及电压互感器延时tf1/us20A/D及电压互感器延时tf2/us20
在该仿真模型的基础上,将改进后的ITM功率接口接入到MMC2侧交流母线与换流变压器之间,对比分析两系统的运行特性,以验证改进接口算法的有效性。下面将从稳定性和精确性两方面进行验证。以下仿真结果中下标orig表示原始系统参数。
3.1ITM接口稳定性验证
通过对双端直流系统传输有功、无功功率发生变化事件进行仿真,来验证所提改进ITM接口算法的稳定性。在0.3 s时将MMC1和MMC2同时投入运行,MMC1运行于Udc=1.0 pu,Q1=-0.1 pu,MMC2运行于P2=0 pu,Q2=-0.8 pu,即STATCOM模式;在1.5 s时,设置P2=0.9 pu,Q2=0 pu。得换流母线2的电压和电流以及与参考系统有功和无功功率对比的波形如图4所示。

图4 稳态运行点变化时系统稳定特性
通过分析以上仿真结果可知:系统运行工况发生变化时,该接口系统可以保持稳定运行,且其有功和无功功率最大偏移量和调整时间基本一致,即动态响应相同,可以快速恢复稳定运行;分析结果表明该改进接口算法具有较高的稳定性,并且几乎不影响控制器的控制性能。
3.2ITM接口精确性分析
为了实现对接口精确性的定量分析,给出如下指标:
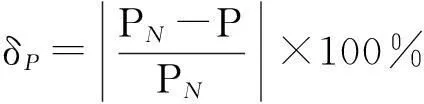
(9)
式中:δP为有功功率稳态相对误差;PN为有功功率参考值;P为实际稳态有功功率。

图5 有功功率稳态相对误差
针对图4中2.5 s后的稳态有功功率,采用公式(9)对两系统稳态误差进行定量计算,得延时为40 us时有功功率稳态相对误差如图5所示。
对仿真结果进行数据分析可得,采用改进ITM接口算法的系统有功功率稳态相对误差最大值为2.01%,大于原始系统相对误差最大值0.73%,这是由接口延时以及回馈电流滤波器等因素引起的系统误差,但由于其相对误差较小,可以满足仿真实验精确性的要求。
4结论
本文研究分析了MMC-HVDC数字物理混合仿真系统的结构,并针对ITM接口算法的稳定性问题,提出引入反馈电流滤波器的改进算法。在此基础上,在PSCAD/EMTDC中搭建了双端MMC-HVDC数字物理混合仿真模型,仿真验证了改进ITM接口的稳定性,并通过对稳态有功功率相对误差的对比分析,揭示了接口延时与滤波器的引入对其精确性的影响。通过研究分析,得出以下结论:
1)在引入反馈电流滤波器的情况下,ITM算法具有较高的稳定域度,系统运行工况变化仍能稳定运行,其动态响应性能与原始系统一致。
2)采用改进ITM接口算法的仿真系统,由于额外引入滤波器,致使其精确性变差,在无法满足仿真研究精确性要求时,需采取延时补偿技术来提高系统的仿真精度。
参考文献
[1]郭小江,申洪,周勤勇,等.特高压交直流混合输电系统安全稳定研究[R].北京:中国电力科学研究院,2010:45-49.
[2]徐政,唐庚,等.柔性直流输电系统[M].北京:机械工业出版社,2012:19-24.
[3]汤广福.基于电压源换流器的高压直流输电技术[M].北京:中国电力出版社,2010:30-36.
[4]Steurer M,Edrington C S,Sloderbeck M,et al.A megawatt-scale power hardware-in-the-loop simulation setup for motor drives[J].IEEE Trans on Industrial Electronics,2010,57(4):1254-1260.
[5]REN W.SLODERBECK M.Interfacing issues in real-time digital simulators[J].IEEE Transactions on Power Delivery,2011,26(2):1221-1230.
[6]RENW.SteurerM,BaldwinTL.Improve the stability and the accuracy of power hardware-in-the-Loop simulation by selecting appropriate interface algorithms[J].IEEE Transactions on Industry Applications,2008,44(4):1286-1294.
[7]胡昱宙,张沛超,方陈,等.功率连接型数字物理混合仿真系统:(一)接口算法特性[J].电力系统自动化,2013,37(7):36-41.
[8]胡昱宙,张沛超,包海龙,等.功率连接型数字物理混合仿真系统:(二)适应有源被试系统的新型接口算法[J].电力系统自动化,2013,37(8):76-81.
[9]胡涛,朱艺颖,印永华,等.含多回物理直流仿真装置的大电网数模混合仿真建模及研究[J].中国电机工程学报,2012,32(7):68-75.
[10] 周俊,郭剑波,胡涛,等.高压直流输电系统数字物理动态仿真[J].电工技术学报,2012,27(5):221-228.
[11] 胡涛,朱艺颖,张星,等.全数字实时仿真装置与物理仿真装置的功率连接技术[J].电网技术,2010,34(1):51-55.
[12] Steurer M,Edrington C S,Sloderbeck M,et al.A megawatt-scale power hardware-in-the-loop simulation setup for motor drives[J].IEEE Trans on Industrial Electronics,2010,57(4):1254-1260.
[13] REN W,STEURER M,WOODRUFF S.Applying controller and power hardware-in-the-loop simulation in designing and prototyping apparatuses for future all electric ship[C]// Electric Ship Technologies Symposium,2007.ESTS’07.IEEE,May 21-23,2007,Arlington,VA:443-448.
[14] VIEHWEIDER A,LAUSS G,FELIX L.Stabilization of power hardware-in-the-loop simulations of electric energysystems[J].Simulation Modeling Practice and Theory,2011,19(7):1699-1708.
[15] 安然然,赵艳军,盛超,等.基于实时仿真的功率连接型数模混合仿真技术研究[J].广东电力,2015,28(2):50-56.
An Improved Interface Algorithm of Power Hardware-in-the-Loop Simulation for MMC-HVDC
LIN Chu-qiao,JIANG Shou-qi,CHEN Hou-he
(Electrical Engineering College,Northeast Dianli University,Jilin Jilin 132012)
Abstract:Power hardware-in-the-loop simulation combines the advantages of physical simulation and real time digital simulation,becoming the key means to study and analyze the complex power system gradually.Power interface algorithm is the key technology of the simulation.In this paper,a power interface algorithm is presented for power hardware-in-the-loop simulation of MMC-HVDC.The necessary condition for the stable operation of the power interface is derived by using the Routh stability criterion,and the improvement measures are put forward to improve the stability by putting converter transformer in the physical side and introducing the feedback current filter.The power hardware-in-the-loop simulation system based on ITM is built in PSCAD/EMTDC,The stability of the algorithm is verified,and the simulation accuracy of the hybrid system and reference system is compared by the results of digital simulation.The simulation analysis shows that the algorithm has good performance of stability and accuracy.
Key words:Modular multilevel converter;Hardware-in-the-loop simulation;Ideal transformer model;Interface stability
收稿日期:2016-01-12
基金项目:国家自然科学基金项目(51477027);国家电网公司科技发展计划项目(〔2015〕90号文);国家电网公司科技发展计划项目(SGRIZLKJ[2015]457号)
作者简介:林楚乔(1989-),男,吉林省长春市人,东北电力大学电气工程学院在读硕士研究生,主要研究方向:柔性直流输电技术.
文章编号:1005-2992(2016)02-0001-06
中图分类号:TM743
文献标识码:A

