基于CFD原理的V形换热器流场分析

吕如兵　刘亚丽　李　嘉（华中科技大学　武汉　430074）



基于CFD原理的V形换热器流场分析

吕如兵刘亚丽李嘉
（华中科技大学武汉430074）

【摘要】针对一款美式风管机上面的V形翅片管式换热器，利用Fluent软件中的多孔介质模型，模拟了V形翅片管式换热器中空气流动的不均匀性分布情况。经过对比分析，表明该模型能够较准确的计算出V形翅片管式换热器空气侧风速的不均匀分布情况。结合翅片管式换热器设计软件EVAP-COND和CoilDesigner软件，计算换热器换热及制冷剂出口状态，合理安排管路布置。

【关键词】V形换热器；气流分布；不均匀性

0　引言

翅片管式换热器广泛的应用于制冷空调装置中，在实际应用当中为了减少换热器所占用的空间，会以一定的角度倾斜放置，例如美式风管机中的V形换热器。换热器与来流风速不是相互垂直，就会导致空气流速在换热器迎风面的不均匀分布。风速的不均匀分布会使换热器的换热性能降低，美国学者Chwalowski研究了同一蒸发器在5种不同风速分布下的性能，研究结果表明在相同风量的条件下风速的非均匀分布引起换热量的衰减达到30%[4]，而且风速的非均匀分布会引起制冷剂侧制冷剂流量的非均匀分布，从而引起换热器换热性能的显著降低。国内也有学者分别研究了几种不同风速分布情况，即上三角、中三角、下三角等截面形状的风速分布对热泵换热器的影响，3种风速分布下的换热量最大差别超过12%[5]。文献[6,7]用实验方法测量了分体式空调器室内换热器表面的二维非均匀风速分布，并用EVAP-COND[2]软件对这一分布下的蒸发器性能进行了研究，表明非均匀风速分布下风速大的管路换热量大，风速小的管路换热量小，且后者减小幅度明显，总的换热量比均匀分布时减少8.5%。以上研究均表明风速的不均匀分布会引起换热器性能的降低。但是对换热器进行设计计算时，一般都假设风速均匀分布或者设定其按一定的规律均匀变化[7,8]，与换热器在实际运行条件下的迎面风速分布存在着一定的差距。

本文采用基于CFD原理的数值模拟方法，利用Fluent软件中的多孔介质模型[1]来模拟V形换热器的迎面风速分布情况，为V形换热器换热性能的优化提供依据，而且解决了用实验手段难以精确测量换热器表面迎面风速分布的难题。

1　研究对象

研究对象是如图1所示的某公司一款美式风管机中的V型翅片管式换热器，其主要的结构尺寸为：Φ9.52mm×0.27mm内螺纹铜管，管排行距=25.4mm，列距=22mm，总U形管的根数为22×2，共44根，单侧有两排管。兼顾管外侧空气流动的压降与换热特性的综合性能来看，开缝翅片的厚度取0.15～0.3mm较为合适，本文中的翅片厚度取0.15mm，翅片类型为弧形百叶亲水翅片，片距为1.6mm，换热管内制冷剂种类为R410a。详细尺寸如表1所示。

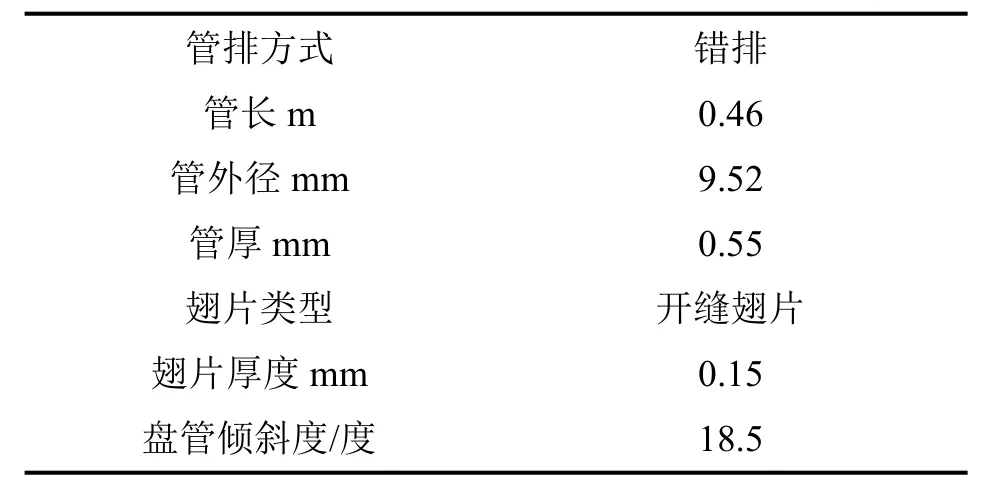
表1　换热器形状参数Table 1 The shape parameter of the heat exchanger

图1　 V形翅片管换热器Fig.1 The V-shaped tube-fin heat exchanger

2　流场分析

2.1计算区域

考虑到V形翅片管式换热器由两块翅片管式换热器板以一定的角度对称布置，且两个换热板的结构也是完全对称的，因此在对换热器进行流体流动计算模拟时，取其对称面的右半部分进行计算。计算模型及网格划分如图2和图3所示，为了更准确的模拟空气流经换热器前后的流动状态，沿计算区域空气进出口方向分别向外做了延伸，这样就可以更清楚的观察空气进入换热器前的流动状态以及经过换热器之后的流动情况。模型采用分区划分网格的方法，由于换热器上下两部分是楔形区域，在对体进行网格划分时采用Hex/Wedge网格元素的Cooper网格画法[9]，体网格总数为5503977个。

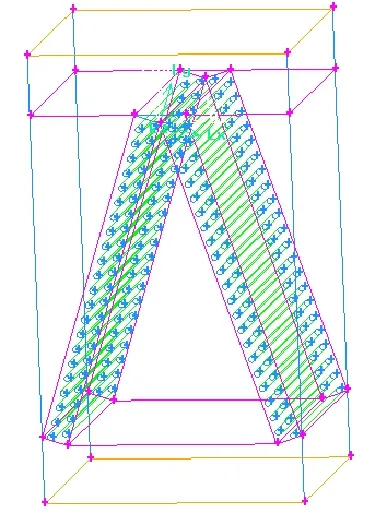
图2　（a）计算区域示意图Fig.2(a) The full domain of computation

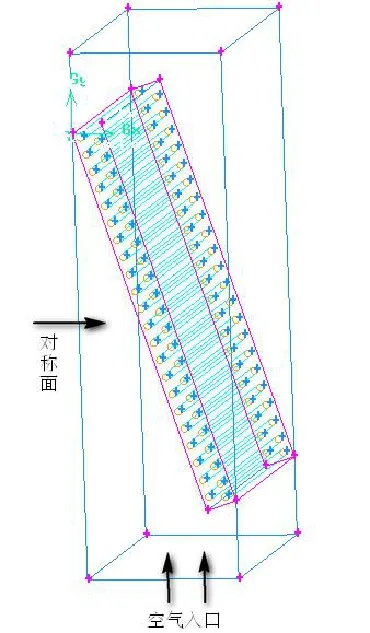
图2　（b）对称计算区域Fig.2(b) The symmetry domain of computation

图3　（a）体网格划分Fig.3(a) The meshing of volume

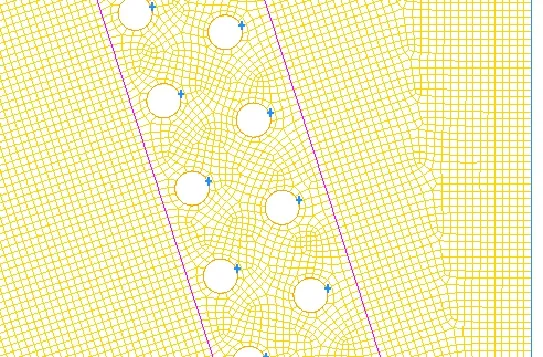
图3　（b）局部放大的体网格Fig.3(b) The local amplified volume mesh

2.2数学模型

2.2.1基本假设

在对换热器进行数值计算时，任何模型都不能全面精确的考虑所有的相关变量，因而需要对模型进行必要的简化假设，这些简化假设包括：

计算区域内空气的流动是稳定的湍流流动；

忽略换热器周围其他附件对空气流动的影响[10]；

翅片管换热器所在区域视为多孔介质，空气从其中通过；

忽略浮力和重力的影响，空气视为不可压缩流体。

2.2.2控制方程

CFD数值模拟是流体流动控制方程的数值求解方法[11]，这些控制方程包括描述流体流动特性的Navier-Stokes控制方程以及流体流动的能量输运方程和组分输运方程组成的封闭方程组。CFD数值模拟中重要的步骤就是压力-速度的耦合方式，本文中压力速度的耦合方式是SIMPLE算法。下面就本次计算过程中涉及到的一些控制方程进行介绍。

首先是连续性方程，本文中假设空气是不可压缩流体，所以公式中的第一项可以忽略，在本文中也没有引入质量源项，所以等式右边的项也可以省去。因此，连续性方程可以简化为：

其次是动量守恒方程，惯性坐标系中的动量守恒方程可以用下面的公式表示，在-→这个-→公式中P是指静压，代表的是应力张量，和分别代表的是重力和外部体积力。

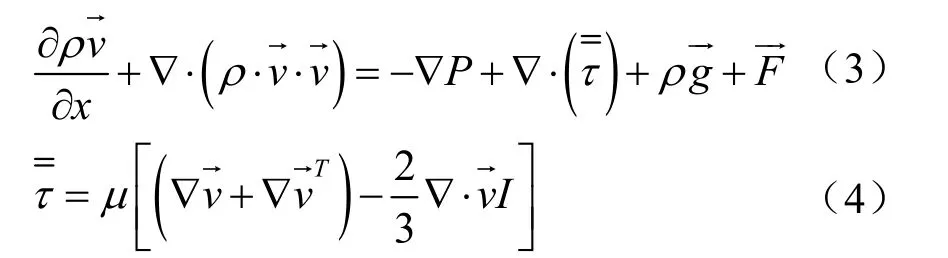
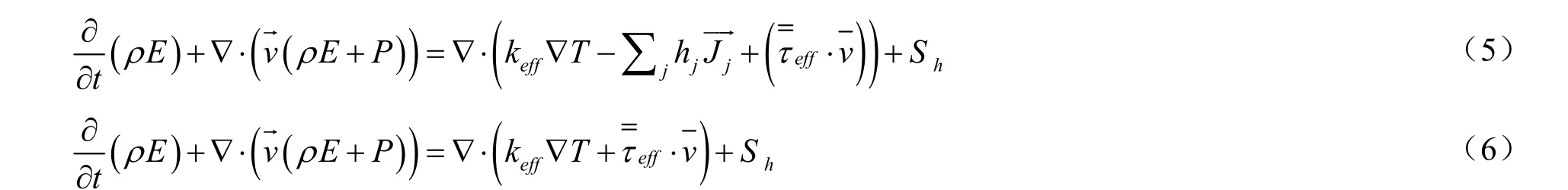
本文主要讨论的是V形翅片管式蒸发器迎面空气流场的分布，不考虑开缝翅片对局部流动的影响[12]，故这里V形翅片管式蒸发器数值模拟采用Fluent中的多孔介质模型[13]，直接在Gambit中建模并划分网格，多孔介质模型的原理即在动量方程中增加了一项包括粘性损失和惯性损失的动量源项，可由下式表示：

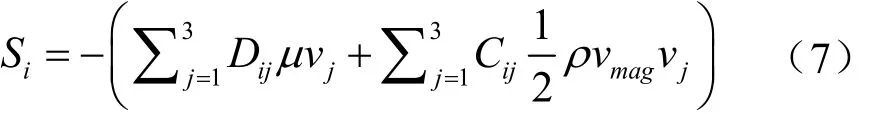
其中：Si为第i个（x、y或z方向）动量方程中的源项；D、C为给定矩阵。

对于规则简单、介质均匀的多孔介质也可以用下式计算：

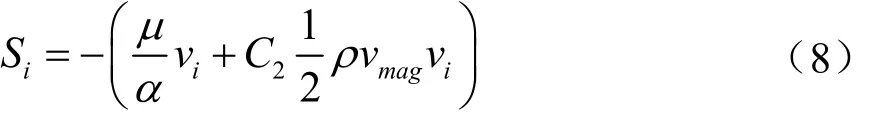
式中：α为多孔介质的渗透率；C2为惯性阻力因子。

2.2.3边界条件

多孔介质模型中惯性阻力因子C2和粘性阻力因子，可以通过测定V形翅片管式换热器在不同迎面风速条件下，空气流经V形翅片管式换热器时产生的压力损失来确定。表2是通过实验测试的经过V形翅片管换热器的气流速度和压降数据。为了能够与公式（8）相对应，对实验数据采用二次多项式形式进行拟合，在matlab软件中采用拟合函数对表2中的数据进行二次多项式拟合，拟合图形如图3所示，多项式拟合结果为：

通过对公式（8）和（9）进行对比联立可得出：

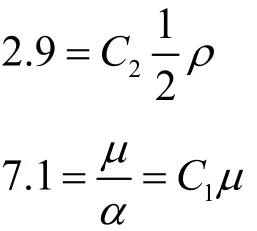
式中：ρ为流体密度，kg/m3；μ为流体动力粘度，Pa·s。

由上面的式子可以得出摩擦阻力因子和惯性阻力因子分别为C1=394444，C2=4.83。由此可以确定换热器所在区域的多孔介质模型中的边界条件参数。

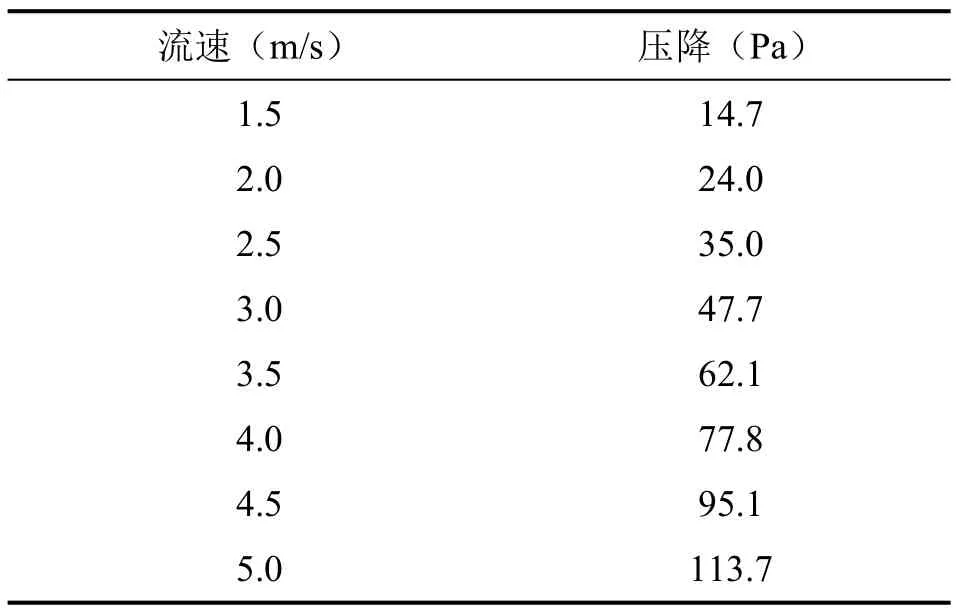
表2　实验测定通过换热器气流速度与压降Table 2 The air velocity and pressure drop through the heat exchanger

2.3数值模拟结果

在Gambit中对三维区域进行仔细的网格划分，并且获得了高质量的网格品质，三维计算区域中有5503977个体网格。在Fluent计算中采用标准的k－ ε湍流模型，数值计算中采用的离散格式为一阶迎风格式，壁面设置为无滑移边界条件。进口风量为0.22kg/s，为了保证换热器迎风面风速不受进口的影响，我们在换热器上方空气入口方向向上延伸114mm，保证入口边界条件是速度入口边界条件，大小是2.0m/s，进口空气的温度设定为恒定的27℃，出口为压力出口；求解器的迭代次数设定为1000，以保证求解迭代的过程中能够得到满足收敛标准的解。残差的收敛标准除了能量方程取外，其他方程的收敛标准取，残差收敛标准如图4所示。

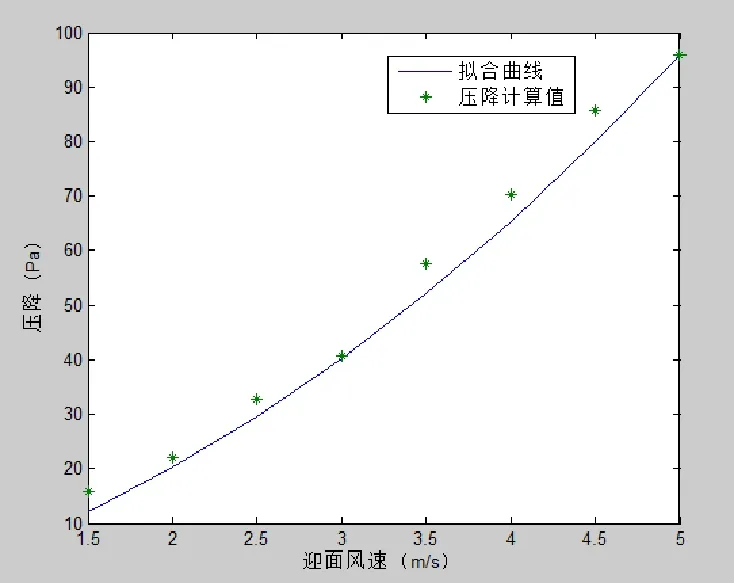
图4　实验数据拟合图形Fig.4 The polyfit of the experimental data

图5显示的是三维计算区域位于两个翅片之间的中心截面，以及在这个截面上的速度矢量。通过风洞试验测定的经过整个换热器的空气侧的压降为24.0Pa，模拟计算的压降为26.2Pa，计算值与实验值之间的误差为9.1%，对于这种倾斜布置的换热器，其结果是符合实际要求的。表明Fluent软件中的多孔介质模型能够用来准确的计算V形翅片管式换热器空气侧流场的分布情况。图6显示的是空气经过V形换热器时的空气流速分布的柱状图。

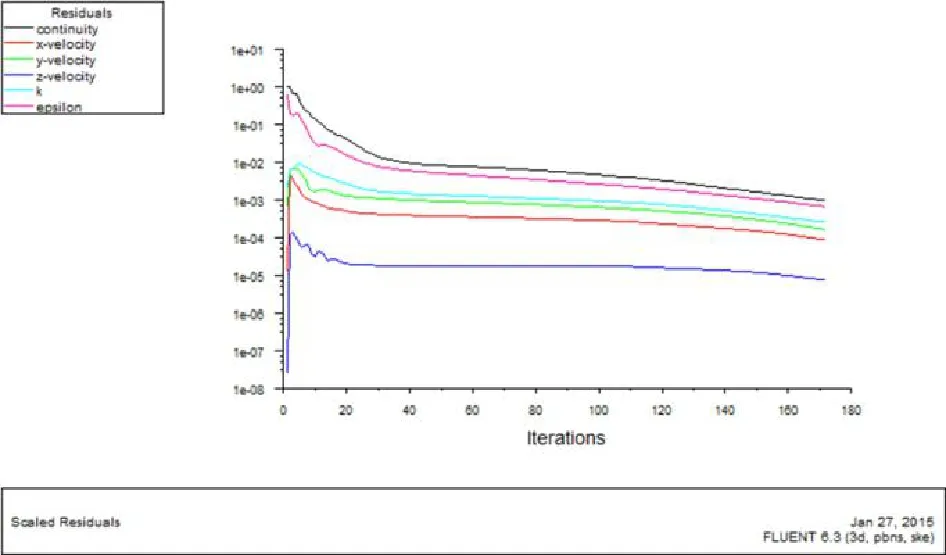
图5　收敛标准Fig.5 Convergence standard

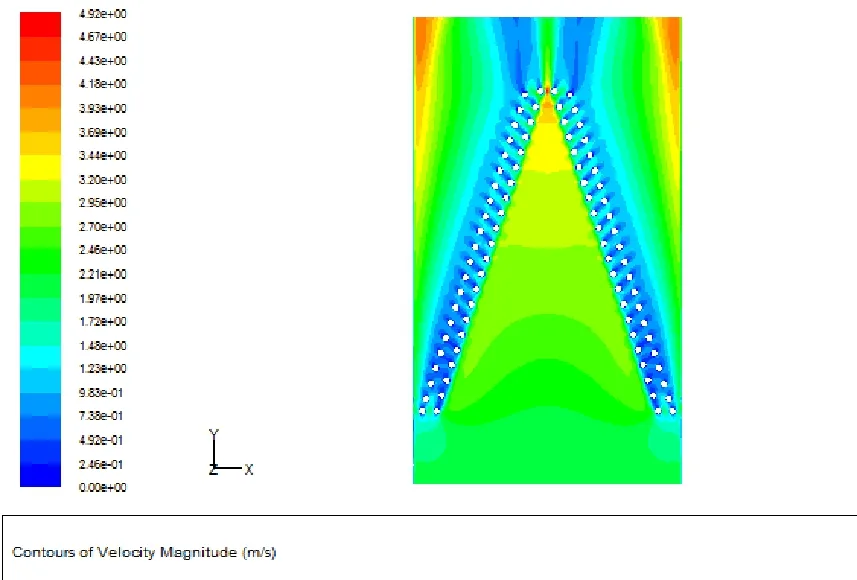
图6　中心截面区域流场分布图Fig.6 The flow field distribution of the center crossection

从图5和图6的实际计算结果可以看出：在进口空气流量为0.2kg/s时，进口处的空气平均流速是2m/s。空气经过V形翅片管式换热器表面时的速度有较大的差别，V形翅片管式换热器上端风速接近进口风速，中间区域速度较小，下端风速比较大，最大可以达到4m/s，70%的区域流速集中0.5-2m/s，有一些区域的流速高达4m/s，且在V形翅片管式换热器两侧下部楔形区域内形成了涡流。

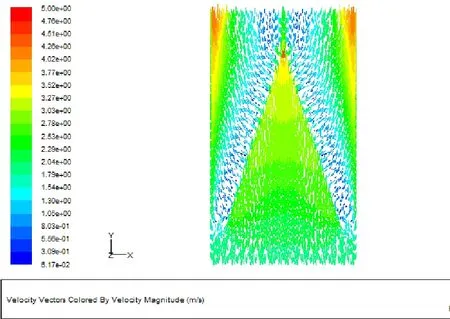
图7　中心截面区域流场速度分布矢量图Fig.7 The air flow velocity vector of the center crossection

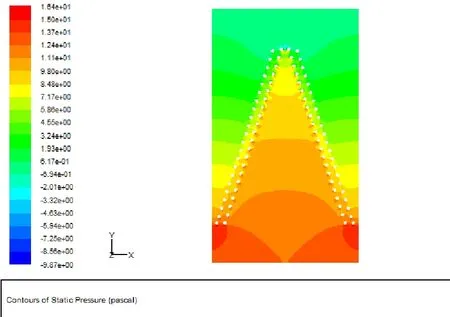
图8　中心截面区域压力分布云图Fig.8 The pressure distribution contour of the center crossection

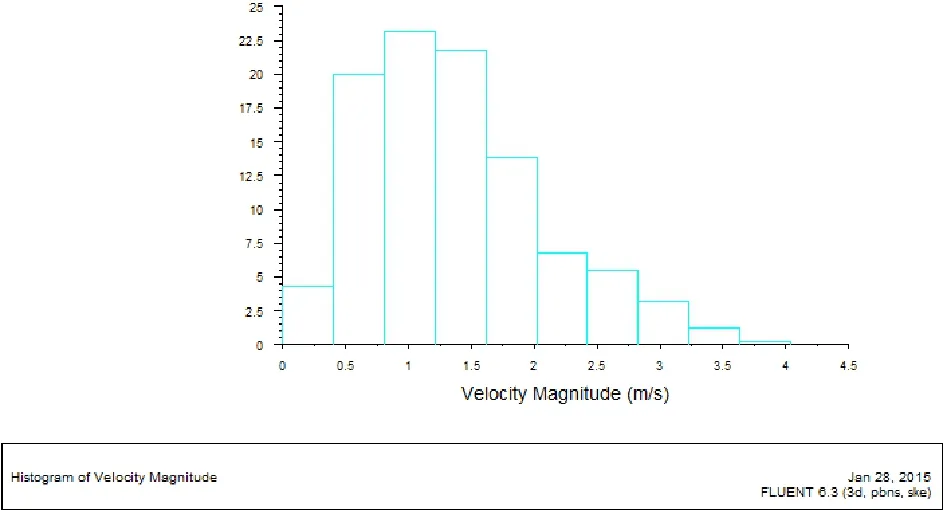
图9　 V形换热器区域气流速度分布柱状图Fig.9 The histogram of the air velocity distribution

3　应用分析

为了验证上述空气流速不均匀性分布对换热器性能的影响，使用基于数值计算方法的换热器设计软件CoilDesigner[3]，对上述V形翅片管式换热器的换热性能进行计算，并比较在实际风速分布条件下各个管路中制冷剂出口状态的不同以及换热量的差别。

3.1边界条件

计算过程中，空气侧空气进口温度采用设计工况下的干球温度27℃、湿球温度18℃，管侧的制冷剂流量和入口状态相同，通过比较上述换热器作为蒸发器时三个管路中每个管路的制冷剂出口的过热度，来判断不同风速分布对蒸发器换热性能的影响。图10是在CoilDesigner中用来计算的换热器管路示意图，它分为上中下三个环路。

图10　 CoilDesigner换热设计中的三个环路（上、中、下）Fig.10 The circuity of the heat exchanger ( top , medium and bottom)

3.2计算结果与分析

计算结果显示三个环路的制冷剂出口过热度分别为：上环路4℃、中间环路2℃、下环路8℃。这和上文计算出的空气流速的大小分布呈现出正相关的特性，即环路所在区域平均风速大的出口制冷剂的过热度大、环路所在区域平均风速小的其制冷剂出口的过热度也较小。

4　结论

应用数值模拟的方法对某型号美式风管机V形翅片管式换热器空气侧空气速度的不均匀分布及其对换热器换热性能的影响进行了研究，得到了V形布置翅片管式换热器空气侧的流场分布及流场分布对换热管内制冷剂换热特性的影响。研究表明：

（1）利用Fluent软件中的多孔介质模型较准确的模拟出了翅片管式换热器空气侧空气速度的不均匀分布情况，V形翅片管式换热器上端风速接近进口风速，中间区域速度较小，下端风速比较大，最大可以达到4m/s，中间区域由于管路间的相互影响而出现波动。

（2）结合上述流场分布的模拟结果，利用换热器设计计算软件CoilDesigner计算了V形翅片管式换热器在制冷运行时换热性能。结果表明，在平均风速大的区域管路制冷剂出口的过热度大，反之则过热度低。

（3）为了保证蒸发器出口的过热度满足设计要求，就需要考虑在设计制造过程中在平均风速大的区域布置较短的制冷剂环路，而在平均风速度较小的区域布置相对较长的管路，以保证制冷剂出口的过热度满足进入压缩机的要求。

参考文献：

[1]邓斌,李欣,陶文铨.多孔介质模型在管壳式换热器数值模拟中的应用[J].工程热物理学报,2004,(S1):167-169.

[2] DOMANSKI P A, DAVID Y, MINSUNG K. Performance of a fined-tube evaporator optimized for different refrigerants and its effect on system efficiency [J]. International Journal of Refrigerant, 2005,28(6): 820-827.

[3] Jiang H, Aute V, Radermacher R. CoilDesigner: a general-purpose simulation and design tool for air-torefrigerant heat exchangers[J]. International Journal of Refrigeration, 2006,29(4):601-610.

[4] A CHWALOWSKI M DIDION D. Verification of evaporator computer models and analysis of performance of an evaporator coil[J]. ASHRAE Trans. 1989.

[5]黄东,孙敏超,贾杰楠,等.风速分布对单流路双排管蒸发器性能影响的模拟研究[J].西安交通大学学报,2009,(5):36-39.

[6]黄东,吴蓓.风速非均匀分布对蒸发器性能的影响[J].西安交通大学学报,2010,(9):6-10.

[7]李权旭,孙敏超,黄东.风速分布对双排管两流路蒸发器性能影响的模拟研究[J].西安交通大学学报,2010,(5): 50-55.

[8]柳成文,王冬青,龚建英.风速分布不均匀性对空气源热泵风侧换热器性能的影响[J].制冷与空调,2008,(3): 87-90.

[9]刘小平,张敏,刘晶,等.商用软件GAMBIT的解析和应用[J].南京工业大学学报:自然科学版,2008,30(1): 101-104.

[10] Mao J N, Chen H X, Jia H, et al. Effect of air-side flow maldistribution on thermal–hydraulic performance of the multi-louvered fin and tube heat exchanger[J]. International Journal of Thermal Sciences, 2013,73: 46-57.

[11]张华廷,吴蔚兰,向灵均.CFD在电子洁净室节能设计中的应用[J].制冷与空调,2013,(6):565-568.

[12]黄亮,李嘉,王晓墨,等.开缝翅片流动与换热特性的数值模拟[Z].中国广东顺德:20085.

[13]韩占忠.Fluent:流体工程仿真计算实例与分析[M].北京:北京理工大学出版社,2009.

The Simulation of V-shaped Heat Exchanger Based on the CFD Theory

Lv Rubing Liu Yali Li Jia
( Huazhong University of Science and Technology, Wuhan, 430074 )

【Abstract】In this paper, we mainly discussed the application of the porous media and distributed resistance model in the software of Fluent in numerical simulation of V-shaped fin-tube heat exchanger. Using this model to simulate the air maldistribution, and compare it with the experimental result. Then we can evaluate the heat transfer performance using the software of EVAP-COND and Coildesigner, and optimize the circuit layout of the fin-tube heat exchanger.

【Keywords】V-shapedheatexchanger; Airflow; Maldistribution

中图分类号TB657.5

文献标识码A

文章编号：1671-6612（2016）01-047-06

作者简介：吕如兵（1989.03-），男，硕士，E-mail：787152795@qq.com

通讯作者：李嘉（1975.08-），男，博士，副教授，E-mail：wxm_hust@263.net

收稿日期：2015-02-02