固定锥形阀消能设施消能效果的数值模拟研究
苏克巴图,童成彪,方 鑫
水工试验
固定锥形阀消能设施消能效果的数值模拟研究
苏克巴图1,童成彪2,方 鑫2
(1.新疆巴州若羌河米兰河流域管理处,新疆巴州841800;2.中阀科技(长沙)阀门有限公司,长沙410007)
针对固定锥形阀的阀后出口水流流速较大的问题,需要在阀后布置相应消能设施来消除多余动能,通过使用VOF方法对锥形阀排出流体的流动状态进行计算模拟,研究和探讨了不同消能设施布置方式对出口水流能量消除的影响。结果表明,合理的锥形阀后消能设施布置能够有效消除阀门出口动能,最大消能率达89.6%。消能效率与消能池深度和池长均同时存在关系,较深且较长的消能池和较浅且较短的消能池布置方案具有较好消能效果。
固定锥形阀;VOF方法;消能;数值模拟
1 引言
固定锥形阀主要用于水利工程大坝放空、水电站机组旁路、水利或水电灌溉系统的流量调节和能量消除[1-2]。该阀门出口水流具有较高流速,一般情况下,水流直接对空排放,通过水与空气之间的掺气作用将动能消除。但实际应用中由于受到场地空间限制,通常不允许锥形阀出口有大范围喷射水流。
针对锥形阀半淹没出流工况,上游水流经过锥形阀的作用将静压能转化为动压能,并冲击下游的消能池等设施,当水流由急流到缓流过程中将会发生水跃现象[3],而水跃具有消能特性,阀后消能池的设计主要原理就是利用可控制水跃来进行消能。
由于锥形阀出口水流流速较高,其在下游消能池中进行消能时,水流流态混乱,三维紊流剧烈,通过经验计算公式难以准确描述其消能效果,而物理模型试验周期长、投资大,随着计算机数值计算技术发展,水流流动模拟计算应用越来越广泛,同时具有较高准确度。数值模拟已经能够比较真实地反映水流运动特性,从而为工程方案优化节省时间,提高研究效率。
2 数学模型
2.1 自由液面的数值模拟方法
利用有限体积法对通过锥形阀的水流在下游消能池中的流动状态进行模拟分析[4],进而研究水流流动特点和消能池的消能效果,为设计合理的消能设施提供参考。水流在消能池中的运动属于明渠流范畴,在进行数值模拟计算过程中将使用到VOF(Volume of fluid)方法[5]来进行水流与空气之间的交界面跟踪计算。
VOF方法是由Hirt和Nichols在1981年提出的处理复杂自由表面的有效方法,是目前应用非常广泛的一种追踪自由表面的数值方法。该方法使用静态或以某种确定形状网格以适应与界面形状的演化。在进行流体力学的数值计算中通过定义流体体积函数VF=F(x,y,z,t)表示计算区域内流体体积占据计算区域的相对比例,对于某个单元,VF=1表示该单元被流体完全充满;VF=0表示该单元是个空单元,没有流体;VF=0~1表示该单元被流体部分充满,VOF法只用一个函数就可描述自由表面的各种复杂变化。
基于VOF方法连续性方程和动量守恒方程描述为式(1)、式(2)。

式中u,v,w为x,y,z方向上的速度;Ax,Ay,Az为单元内x,y,z方向上可流动的面积分数;Ui为i方向上的速度,i为x,y,z 3个方向;VF为单元内流体体积分数;ρ为流体密度;xi为i方向坐标,i为x,y,z3个方向;p为流体压力;Gi为x,y,z方向上的重力加速度;fi为x,y,z方向上的黏滞力。
2.2 RNG k-ε湍流模型
在流体数值模拟计算中,若流动状态为湍流,则直接求解N-S方程将消耗巨大的计算机资源和时间,故实际工程中湍流问题处理主要是对瞬态N-S方程进行时间平均处理,同时补充反映湍流特性的其他方程使控制方程组封闭,进而使方程存在唯一解。
对于湍流流动数值方法,工程上通常采用标准k-epsilon两方程模型[6]进行求解计算,而对于具有强旋流的高雷诺数问题,RNG k-epsilon模型[7]则具有更准确的描述,其湍动能方程和湍动能耗散率方程为式(3)、式(4)。

式中ρ为密度;k为紊流动能;ε为紊流动能耗散率;ui为速度;μ为黏度;μt为紊流粘度;σk为k值的紊流普朗特数;σε为ε值的紊流普朗特数;Pk为由于平均速度梯度产生的紊流动能;C1ε为常数1.42;C*2ε为常数1.68。
3 锥形阀后消能设施数值计算
在锥形阀后的消能池中,水跃现象将泄水建筑物泄出的急流转变为缓流以绝大部分消除动能,进而防止高速水流冲刷下游水工建筑物。水跃消能主要靠水跃产生的表面旋滚及旋滚与底流间的强烈紊动﹑剪切和掺混作用。由于水跃流态复杂,水流波动剧烈,应用数值模拟方法对其进行研究得到越来越广泛的应用。一般情况下锥形阀后空间较小,且附近存在多种水工建筑物,在设计下游消能设施时,宜选用消能池加消能坎的综合消能形式。针对此综合式消能池设计,主要考虑参数为消能坎高c、消能池深S和消能池长度Lk等。
数值计算区域主要包括锥形阀上游入口管道,固定锥形阀及阀下游消能设施,计算模型设计如图2。模拟计算过程中设置上游入口总水头为50m,下游出口为自由出流,压力大小为大气压,管道和消能池壁设为无滑移的壁面边界条件,而固定锥形阀的通径则设置为2000mm。

图1锥形阀消能设施设计
图2 和图3中为计算区域内压力分布云图和速度分布云图,表明压力和速度在固定锥形阀前和阀后变化较大,在锥形阀后压力出现较大程度降低,且阀出口位置速度最大。由此可知,上游水流经过锥形阀作用之后,将其压力能转换为动能并进入消能池中,由于速度剧烈变化导致消能池中水流波动剧烈而产生水跃现象,在此过程中绝大部分能量被消除,故在下游出口位置的速度和压力降到最低,达到消能的效果。

图2 压力分布云图

图3 速度分布云图
计算区域内的流体湍动能分布情况如图4。由湍动能分布特点可知,在消能池内和消能池出口位置的水流湍动能较大,表明这些位置湍流较为剧烈,能量消除主要在该处进行。

图4 湍动能分布
根据数值模拟结果得到水流在沿流动方向上速度变化特点如图5,可以发现,水流在上游具有较高速度和水头,然后在通过固定锥形阀时由于导流锥作用使流体压力能转化为动能,故其速度瞬间增大并流入下游消能池中,由于消能池作用而使其速度又瞬间降低并产生水跃,水跃产生表面旋滚及旋滚与底流间的强烈紊动﹑剪切和掺混作用使水流绝大部分能量被消除掉,水跃之后其速度有一定回升,在整个过程中能量被消除而出流速度较小,不会对下游水工建筑物造成冲刷。

图5 沿流动方向的速度变化情况
在进行数值计算的过程中,主要考虑消能池总深度和长度对锥形阀后出口水流消能效果的影响,故在相同上游水头条件下,设置不同消能设施布置方案,进而考察和比较其消能情况。
根据水力学理论,流体能量主要分为两部分,静止流体所具有的静压能及流体分子运动过程中的动压能。所以在分析消能池的消能特点时,采用比较上游和消能池出口的总压降低的程度,从而比较不同结构消能设施的消能效果。计算区域内流体介质能量计算按照式(5)进行[8]。

式中P为流体具有的静压值;ρ为流体具有的密度;g为重力加速度;v为选取截面的平均流速。
为了比较消能效果的优异程度,引入消能效率概念,从而利用比较消能效率的大小来评价不同消能设施所产生的消能效果,计算方法如式(6)。

式中K为消能效率;Ein为阀前水流具有的能量;Eout为阀后水流具有的能量。
通过CFD计算分析,在获得计算区域内流体流动分布情况基础上,利用式(5)和式(6)对数值模拟结果进行处理得到消能效率,不同的消能设施布置方案和消能率的大小如表1。D为图1中锥形阀公称直径。

表1 消能设施布置及消能率
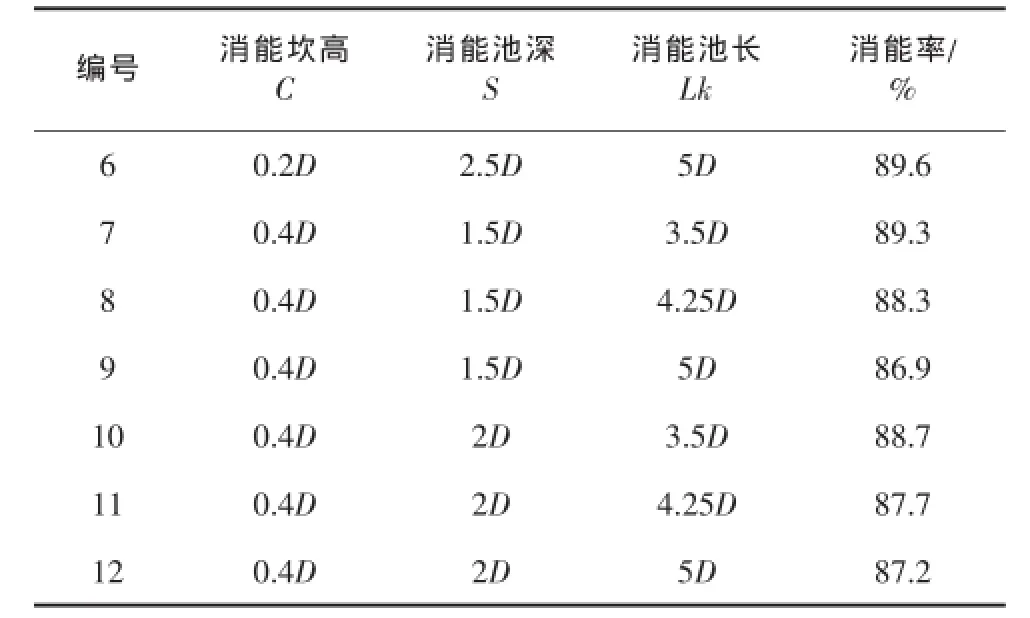
续表1
数值模拟结果表明,锥形阀后的消能设施能够有效消除阀门出口动能,消能率最大可达89.6%。在池深较浅时候,消能池对水流消能率随池长的增加而降低;而在池较深时则情况相反。消能池的消能效率与深度和池长均同时存在关系,较深且较长消能池和较浅且较短消能池布置方案具有较好的消能效果,如考虑建造成本则优先使用较深且较浅消能池布置方案。
为了研究不同流动边界下相同的消能设施设置的消能效果变化情况,以下使用编号6的消能池设计方案进行计算分析。系数描述如式(7)[9]:

式中v为锥形阀出口水流速度;g为重力加速度;h为下游消能池水深。
在进行数值模拟过程中,锥形阀上游设置不同总水头大小,进而改变了进入消能池水流流速,其弗劳德数亦变化,比较其消能效率的变化情况,根据模拟结果得到弗劳德数与消能效率的关系,如图6。

图6 不同弗劳德数下的消能效率情况
由图6可知,设置消能池后能够有效消除锥形阀出口水流动能,流动状态越湍急,弗劳德数越高,则消能效率越高;消能率随着弗劳德数的减小而有所降低,但在一定的弗劳德数范围内,合理设置下游消能池的尺寸方案布置能够消除绝大部分水流动能,从消能池出来的水流具有较低能量,速度较低,不会对下游水工建筑物造成冲刷等影响。
4 结语
(1)运用CFD技术对锥形阀出口水流的流态情况进行数值模拟,通过计算能够较好确定各主要尺寸值,优化了消能设施的布置和设计。
(2)依靠VOF方法在数值计算过程中进行表面定位、跟踪及演化,能够精确计算出流体表面变化和分布情况,是目前应用最为广泛的自由液面数值处理方法。而RNG k-epsilon湍流模型则能够更好地处理具有强旋流的高雷诺数流动问题。
(3)通过CFD计算分析,消能率将高达87%,消能池的消能效率与消能池的深度和池长均同时存在关系。消能池的消能效率随着弗劳德数的增大而升高。数值模拟结果能够为合理布置和设计阀后消能设施提供有力参考。
[1]M.C.约翰逊,刘洪波.锥形固定阀消能[J].水利水电快报,2001,22(24):7-8.
[2]李翠艳,张宗孝,邓莹莹.锥形阀消力池优化试验研究[J].电网与水力发电进展,2008,24(3):54-56.
[3]李炜.水力计算手册[K].北京:中国水利水电出版社,2006.
[4]张永学,李振林.流体机械内部流动数值模拟方法综述[J].流体机械,2006,34(7):34-38.
[5]Hirt,C.W.;Nichols,B.D."Volume of fluid(VOF)method for the dynamics of free boundaries",Journal of Computational Physics.1981,39(1):201-225.
[6]B.E.Launder,D.B.Spalding.Lectures in Mathematical Models of Turbulence.Academic Press,London,1972.
[7]V Yakhot,SA Orszag.Renormalization-group analysis of turbulence.Physical review letters.1986,57(14):1722-1724.
[8]D Stephens,MC Johnson,ZB Sharp.Design Considerations for Fixed-Cone Valve with Baffled Hood.Journal of Hydraulic Engineering,2011,138(2):204-209.
[9]Newman JN.Marine hydrodynamics[M].The MIT Press,1977.
Numerical Simulation of the Energy Dissipation Device of Fixed-Cone Valve
SU ke ba tu,TONG Cheng-biao,FANG Xin
(1.Bazhou Milan Ruogiang River Basin Management Office,Bazhou 841800,China;2.China Valve Technology(Changsha)Co.,Ltd.,Changsha 410007,China)
Since the outlet of fixed-cone valve has a high velocity,some energy dissipation device after the valves must be laid out to eliminate the extra kinetic energy,The flow condition of fluid discharged from the fixed-cone valve would be simulated with the VOF method in the paper,and the influence of different energy dissipation device layout plans were studied and discussed.The results of numerical simulation showed that,Reasonable energy dissipation device behind the fixed-cone valve can effectively eliminate the kinetic energy after the outlet of the valve,the dissipation ratio can reach as high as 89.6%.Both the depth and length of the energy dissipation pool have relationship with the efficiency of energy dissipation,a deeper and longer pool or a shallower and shorter pool can get a better energy dissipation result.
Fixed-cone valve;VOF method;Energy dissipation;Numerical simulation
TV653
A
1672-9900(2016)04-0070-04
2016-06-08
苏克巴图(1972-),男(蒙古族),新疆和静人,工程师,主要从事水利工程设计、施工工作,(Tel)18009965322。

