On the Same n-Types for the Wedges of the Eilenberg-Maclane Spaces∗
Dae-Woong LEE
1 Introduction
Let us call X(n)the n-th Postnikov approximation of a connected CW-space X.X(n)is a CW-complex obtained from X by adjoining cells of dimension ≥ n+2 such that πi(X(n))=0 for i≥ n+1 and πi(X(n))= πi(X)for i≤ n.The Postnikov k-invariants kn+1(X)of X are maps X(n−1)→ K(πn(X),n+1)and thus cohomology classes in Hn+1(X(n−1);πn(X))for n≥2.We say that two connected CW-spaces X and X?have the same n-type if the n-th Postnikov approximations X(n)and X?(n)are homotopy equivalent for all n≥1.
An interesting question raised by J.H.C.Whitehead is this:Suppose that X and X?are two spaces whose Postnikov approximations,X(n)and X?(n),are homotopy equivalent for each integer n.Does it follow that X and X?have the same homotopy type?It is well known that either if X isfinite dimensional(use the cellular approximation theorem)or if X has only a finite number of nonzero homotopy groups,then the answer to Whitehead’s question is yes!However,in general,there are examples,founded by Adams[1]and Gray[6]independently,saying that the answer to this question is no!It is also shown that in[16]if the base space of a sphere fibration ξ:is a topological manifold,then a Hopf index theorem can be obtained.
Let Z be the ring of integers and let Σ denote the suspension functor.For a connected CW-space X,we let SNT(X)denote the set of all homotopy types[X?]such that the Postnikov approximations X(n)and X?(n)are homotopy equivalent for all n.This is a pointed set with base point∗=[X].It is well known in[11]that the set of all the same homotopy n-types for the k-th iterated suspension of the Eilenberg-MacLane space K(Z,2b+1)is trivial for k≥0;that is,SNT(ΣkK(Z,2b+1))= ∗.One reason of this fact is that ΣkK(Z,2b+1)has a rational homotopy type of a single sphere of dimension k+2b+1.As we can see,the even dimensional case is much more complicated because ΣK(Z,2a)has a rational homotopy type of a bouquet of in finitely many spheres of dimensions 2a+1,4a+1,···,2na+1,···.So it is natural to ask in the case of even integers.The first interesting case(a=1)is the following conjecture.
Conjecture 1.1(see[11,p.287])SNT(ΣK(Z,2))= ∗.
The positive answer to this conjecture was given in[8].More generally,what will happen in the case of the suspension of the wedge products of the Eilenberg-MacLane spaces of various types?After suspensions or wedge products of the Eilenberg-MacLane spaces K(Z,2a)and K(Z,2b+1)for a,b≥1 as the in finite loop spaces,they become much more intractable,and they are worth mentioning what it is in the SNT-sense.The purpose of this paper is to provide an answer to the above query as a general version of the original same n-type conjecture.
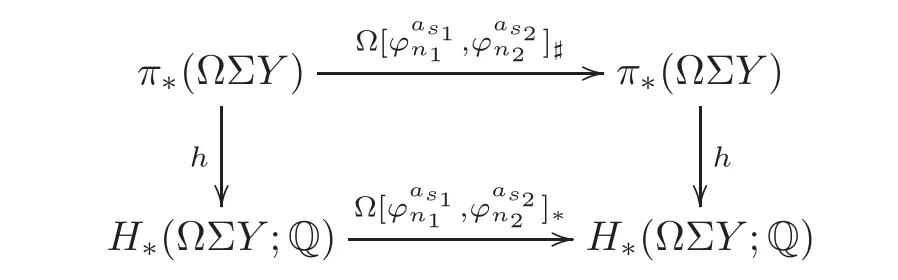
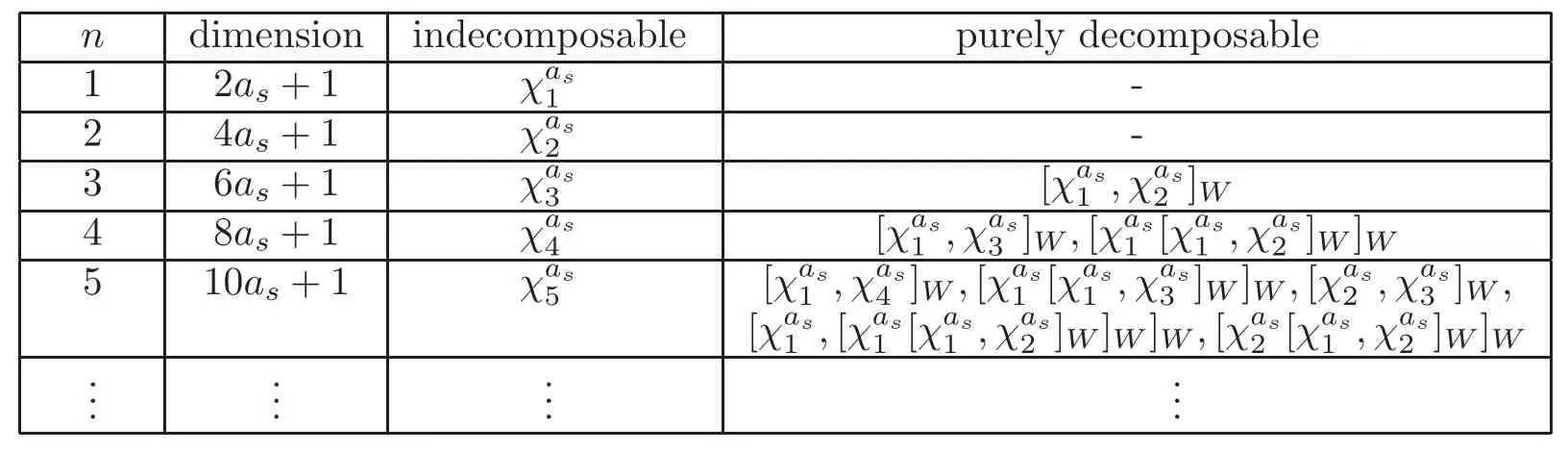
Theorem 1.1Let Y:=K(Z,2a1)∨ K(Z,2a2)∨ ···∨ K(Z,2ak)be the wedge products of the Eilenberg-MacLane spaces,where aiis the positive integer for i=1,2,···,k with a1 In this paper we often do not distinguish notationally between a base point preserving map and its homotopy class.We denote Q by the set of all rational numbers.As an adjointness,we will make use of the notations Σ and Ω for the suspension and loop functors in the based homotopy category,respectively. Let Aut(X)be the group of homotopy classes of homotopy self-equivalences of a space X and let Aut(π≤n(X))denote the group of automorphisms of the graded Z-module,π≤n(X),preserving the Whitehead product pairings.McGibbon and Møller(see[11,Theorem 1])proved the following theorem. Theorem 2.1Let X be a 1-connected space with finite type over some subring of the rationals.Assume that X has the rational homotopy type of a bouquet of spheres.Then the following three conditions are equivalent: (a)SNT(X)=∗; (b)the maphas a finite cokernel for each n; (c)the maphas a finite cokernel for each n. In 1976,Wilkerson(see[21,Theorem I])classified CW-spaces having the same n-type up to homotopy,and proved that for a connected CW-complex X,there is a bijection of pointed sets where lim1is the first derived limit of groups(not necessarily abelian)in the sense of Bous field and Kan[4].Thus,if X is a space of finite type,then the torsion subgroup of π∗(X(n))can be ignored in the lim1-calculation(see[12]). We note that Y has a CW-decomposition of wedges based on the Eilenberg-MacLane spaces K(Z,2as)as follows: for s=1,2,···,k,where γnis an attaching map,anddenotes the other cells or the Moore spaces for torsions of the reduced homology groups for n=1,2,3,···. In order to define the homotopy self-maps of the suspension of wedges of the Eilenberg-MacLane spaces K(Z,2as),s=1,2,···,k,we first define maps:Y → ΩΣY for s=1,2,···,k and n=1,2,3,···as follows. definition 2.1Let for each s=1,2,···,k,and let Ytdenote the t-skeleton of Y:=K(Z,2a1)∨ K(Z,2a2)∨ ···∨K(Z,2ak).Then the co fibration sequences and induce the exact sequences of groups and for n ≥ 2 and s=1,2,···,k.We now take essential maps and for n ≥ 2 and s=1,2,···,k.Similarly,we can choose maps and withand s=1,2,···,k,respectively,by using the above exact sequences. In the above definition,we note that and We now have the following definition. definition 2.2We define the rationally non-trivial homotopy elementsandof the homotopy groups modulo torsions π2as(ΩΣY)/torsion and π2nas(ΩΣY)/torsion by=andrespectively,for s=1,2,···,k and n ≥ 2. We now take the self-maps:ΣY → ΣY and maps:S2nas+1→ ΣY as the adjointness of:Y→ ΩΣY and:S2nas→ ΩΣY,respectively,for s=1,2,···,k and n=1,2,3,···.We then order the basic Whitehead products(see[7])of weight 1 on the graded homotopy groups modulo torsion,π∗(ΣY)/torsion,as follows:We order the rationally non-trivial elementsandaseither ifor ifand as LetΣY → ΣY be the commutator of self-mapsand;that is where the operations are the suspension additions on ΣY.By using this suspension structure,we construct self-maps of ΣY by I+where I is the identity map of ΣY andis the l-th iterated commutator of self-maps:ΣY → ΣY,i=1,2,···,l on the suspension structure for si=1,2,···,k,and ni=1,2,3,···.The Whitehead theorem asserts that the above self-mapsof ΣY are actually homotopy self-equivalences. We note that the above iterated commutator maps do make sense because there are in finitely many non-zero cohomology cup products in Y so that it has the in finite Lusternik-Schnirelmann category(see[20,Chapter X]and[18]).Moreover,Arkowitz and Curjel(see[2,Theorem 5])showed that the n-fold commutator is of finite order if and only if all n-fold cup products of any positive dimensional rational cohomology classes of a space vanish. Remark 2.1(a)Let x be a rationally non-trivial indecomposable element of the homotopy groups π2(n1as1+n2as2+··+nlasl)+1(ΣY).Then where the first addition is the one of suspension structure on ΣY,while the second addition refers to the one of homotopy groups(see[8,Lemma 3.2]). (b)Let J:Y→ΩΣY be the James map.Then we have in the group[Y,ΩΣY](see also[9,Lemma 4]). By using the Serre spectral sequence of a path space fibration for each s=1,2,···,k,we have an algebra isomorphism H∗(K(Z,2as);Q) ∼=Q[αs].Here Q[αs]is the polynomial algebra over Q generated by αsof dimension 2as;that is,αsis a generator of H2as(K(Z,2as);Q)withwhereis a rational homology generator of dimension 2nas. We point out that the proof of Theorem 1.1 depends highly on Theorem 2.1.We remark that the total rational homotopy group= π∗(ΩΣY)⊗ Q of ΩΣY is a graded Lie algebra over Q with Lie bracket?,?given by the Samelson product which is called the rational homotopy Lie algebra of ΣY(see[14]for the de Rham homotopy theory).For s=1,2,···,k and n=1,2,3,···,we letdenote the subalgebra of?L generated by all free algebra generators of degree less than or equal to 2nas,that is with generators(ΩΣYQ)so that njasi≤nas,whereis the compositionof the rationally non-trivial indecomposable elementΩΣY offor si=1,2,···,k and nj=1,2,3,···with the rationalization r:ΩΣY → ΩΣYQ.As an adjointness, with the Whitehead product[,]Whas the graded quasi-Lie algebra structure which is called the Whitehead algebra with generators Remark 3.1We consider the following co fibration sequence: where are the rationally non-trivial homotopy elements.By considering the homotopy co fibre of the above Whitehead product map and the cohomology cup product argument on it,we can see thatis rationally non-trivial,and that by induction on l the iterated basic Whitehead productsin the graded homotopy group π∗(ΣY)/torsion are also rationally non-trivial(see[10,Lemma 3.5]for details). Thus we can define the following. definition 3.1The basic Whitehead productis said to be a purely decomposable generator of the rational homotopy group in dimension 2(n1a1+n2a2+ ···+nlal)+1 if s1=s2= ···=sl,and it is said to be a hybrid decomposable generator if there is at least one siwhich differs from one of those sj,where i ∈ {1,2,···,l}and j=1,2,···,l. Recall that as a graded Z-module and as a graded Q-module,whereandare the standard generators of the homology groups H2nas(Y;Z)/torsion and H2nas(Y;Q),respectively for n=1,2,3,···and s=1,2,···,k.The Bott-Samelson theorem(see[3])says that the Pontryagin algebra H∗(ΩΣY;Q)is isomorphic to the tensor algebra TH∗(Y;Q)generated by=1,2,3,···and s=1,2,···,k}. Let:Y −→ ΩΣY be the adjoint of the iterated commutator mapΣY −→ ΣY.Then we have since the map:[ΣY,ΣY]−→ [Y,ΩΣY]defined by is an isomorphism of groups,where ϕ ∈ [ΣY,ΣY],y ∈ Y,t∈ I and?y,t?∈ ΣY.Moreover,we have the following lemma. Lemma 3.1Let j:Yt?→ Y and q:Yt→ Stbe the inclusion map and the projection to the top cell of Yt,respectively.Then the following diagram is commutative up to homotopy,where t=2(n1as1+n2as2+···+nlasl)andis the iterated Samelson product. ProofWe first consider the exact sequence induced by a co fibration sequence Let:Y →Y ∧Y be the reduced diagonal map(i.e.,the composite of the diagonal Δ:Y →Y×Y with the projection π:Y×Y→Y∧Y onto the smash product)and let pni,asi:Y→Y/Y2niasi−1be the projection for i=1,2.Then by using the cellular approximation theorem,and considering the cell structure of Y∧Y and the composition with we haveFrom the above exact sequence,there exists a map such that By using this fact,we now consider the following commutative diagram up to homotopy(see also[13]in the case of the in finite complex projective space): where t=2(n1as1+n2as2)and C:ΩΣY ∧ΩΣY → ΩΣY is the commutator map with respect to the loop operation,that is Here the multiplication is the loop multiplication and the inverse means the loop inverse ν:ΩΣY → ΩΣY defined by ν(ω)= ω−1,where ω−1(t)= ω(1−t),t∈ [0,1].It shows that The proof in case of the l-fold iterated commutators and the Samelson products goes to the same way by substitutingandrespectively(similarly for the iterated Samelson products of homotopy classes). Lemma 3.2Let h:π∗(ΩΣY)→ H∗(ΩΣY;Q)be the Hurewicz homomorphism.Then whereis the standard generator of rational homology in dimension 2(n1as1+n2as2+ ···+ ProofBy applying homology to the above homotopy commutative diagram(3.2)in the case of the two-fold commutators and the Samelson products,we obtain in rational homology of ΩΣY.Here nas=n1as1+n2as2andis the standard generator of H2(n1as1+n2as2)(Y;Q).The homotopy commutative diagram(3.1)in Lemma 3.1 shows that this lemma is still true for the l-th iterated commutators and the iterated Samelson products,as required. By considering the cell structure of the product of CW-spaces(this works for countable CW-complexes or when one factor is locally finite),we have the following lemma. Lemma 3.3If X is a CW-complex of finite type with base point x0as the zero skeleton and if f and g:X → ΩX?are the base point preserving maps withrespectively,then the restriction of the commutator[f,g]:X→ΩX?to the(p+q)-skeleton of X is inessential. ProofFor details,see[10,Lemma 2.3]. Lemma 3.4Let t=2(n1as1+n2as2+ ···+nlasl).Then is inessential,where si=1,2,···,k and ni=1,2,3,···for i∈ {1,2,···,l}. ProofWe prove this lemma by induction on l.Sinceandfor s=1,2,···,k,and n=1,2,3,···,by Lemma 3.3,we seeiithat the commutatorrestricts to the trivial map on the skeleton Y2(na+na)−2.1s12s2By considering the cell structures of the Eilenberg-MacLane spaces described above,we see that Y has no cells in some ranges of dimensions,more precisely,between dimensions 2n1as1+2n2as2−2 and 2n1as1+2n2as2−1,that is The cellular approximation theorem shows that the restrictionto the skeleton is null homotopic. We now suppose thatis inessential.Sincethe similar argument as described above shows that By induction on l,we complete the proof of this lemma. Lemma 3.5For each basic Whitehead productof the graded homotopy group π∗(ΣY),we can construct the corresponding iterated commutatorin the group[ΣY,ΣY]such that where λ0,andandare rationally non-trivial indecomposable elements,and nas=n1as1+n2as2+ ···+nlasl. ProofWe argue about a matter with induction on l again.We first show that where λ?0,and nas=n1as1+n2as2.To do this,we consider the following commutative diagram: The Cartan-Serre theorem(see[5,Theorem 16.10])asserts that the Hurewicz homomorphism h:π∗(ΩΣY)→ H∗(ΩΣY;Q)becomes an isomorphism where the latter is a primitive subspace of H∗(ΩΣY;Q).Thus we observe that for each s=1,2,···,k and n=1,2,3,···(compare with the Hurewicz map of the Brown-Peterson spectra in[15,p.166]).Hereis the rationally non-trivial indecomposable element of the homotopy groups,andis the rational homology generator in dimension 2nas,where E:Y→ΩΣY is the canonical inclusion.We now have It can be noticed that the above zero term is derived from the fact that the restrictionto the skeleton is inessential by Lemma 3.4;that is for dim()≤ 2(n1as1+n2as2)−1 in rational homology of ΩΣY.Moreover,we see thatandare rationally non-trivial indecomposable and decomposable elements,respectively,in π2(n1as1+n2as2)(ΩΣY)/torsion,by Remark 3.1 as adjointness for decomposable generators,and thatis spherical,and thus primitive.Now considering the above equation(3.3),we observe that On the other hand,is a loop map,thus it is an H-map.Furthermore,the Scheerer’s theorem(see[17,p.75])says that there is a bijection between[ΣY,ΣY]and the set[ΩΣY,ΩΣY]Hof homotopy classes of H-maps ΩΣY → ΩΣY.Therefore,by taking the adjoint of the Samelson product,we obtain the result. We now suppose that the result holds for the(l−1)-fold Whitehead product.Since and the iterated Samelson productis rationally non-trivial,by using the first result above and combining with:Y→ΩΣY,we can construct an iterated commutator mapsuch that,after taking the adjointness,the desired formula of this lemma is obtained. Remark 3.2We turn now to the other types of purely decomposable generators,namelyandconsisting of the basic Whitehead products of the rational homotopy.It can be shown that we can also consider the iterated commutatorsand(corresponding to the basic Whitehead productsandrespectively)satisfying Lemma 3.5 whose proof goes to the similar way. By using the results described above,we now proceed to the proof of Theorem 1.1 as follows. If X is a connected H-space of finite type,then X has k-invariants of finite order,and H∗(X;Q)becomes a Hopf algebra which is the tensor product of exterior algebras with odd degree generators and polynomial algebras with even degree generators.On the space level,this means that every H-space has a rational homotopy type of a product of rational Eilenberg-MacLane spaces.The Eckmann-Hilton dual of the Hopf-Thom theorem(see[19,p.263–269]and[20,Chapter III])says that ΣK(Z,2as)has the rational homotopy type of the wedge products of the in finite number of spheres,that is for each s=1,2,···,k.By using both the basic Whitehead products and the Hilton’s theorem(see[7]),we can find various kinds of rational homotopy indecomposable and purely decomposable generators on π∗(ΣY)⊗ Q as follows: Table 1 s=1,2,···,k Moreover,we can see that there exist hybrid decomposable generators of the rational homotopy.The hybrid decomposable generator might be occurred firstly in dimension 2a3+1.For example,if a1=1,a2=3 and a3=4,thenandare the hybrid decomposable generators in π9(ΣY)⊗Q and π17(ΣY)⊗ Q,respectively.The number of purely or hybrid decomposable generators increases dramatically as the homotopy dimensions are on the increase. Since the ranks between the graded homotopy group modulo torsion and the graded rational homotopy group coincide with each other,we can also find the corresponding indecomposable and decomposable elements on π∗(ΣY)/torsion.More precisely,it can be seen from the above table that there is only one indecomposable generator,up to sign,of the homotopy group π2nas+1(ΣY)/torsion for each n=1,2,3,···and s=1,2,···,k,while there are various kinds of purely or hybrid decomposable generators in it(possibly)for n≥2. We now let L=(π∗(ΣY)/torsion,[,]W)and L≤as,n=(π≤2nas+1(ΣY)/torsion,[,]W)be the Whitehead algebras(corresponding to L and L≤as,n,respectively)under the Whitehead products.And we denoteandby the indecomposable and decomposable components,respectively,of the homotopy group modulo torsions,namely,π2nas+1(ΣY)/torsion.Then we have thatand thusfor each s=1,2,···,k and n=1,2,3,···.Moreover,the following sequence is exact for each s=1,2,···,k and n=1,2,3,···(see[11]).Here the map f sends to and the map g is given by restriction and projection,where q:is the projection and j:is the inclusion.We observe that the above short exact sequence is still valid since we are working on π≤2nas+1(ΣY)/torsion.Furthermore,we get Aut(π2as+1(ΣY)/torsion) ∼=Z2for s=1,2,···,k,and Aut(π≤2nas+1(ΣY)/torsion)is in finite for all n ≥ 3 and s=1,2,···,k.Therefore the induction step begins.We now suppose that the map Aut(ΣY)→ Aut(L completely depending on the form ofsuch that the restrictionto the subalgebra L where λ0,and nas=n1as1+n2as2+ ···+nlasl.By considering the indecomposable and(purely or hybrid)decomposable generators,induction hypothesis and Theorem 2.1,we finally complete the proof of Theorem 1.1. Remark 3.3One may wonder why the k-th suspensions are not mentioned in this paper(or the previous papers[9–10])for k ≥ 2.Indeed,the homotopy self-equivalences I+constructed in our main theorem are not as well behaved as one might wish on the self-maps of the k-th suspension of a given CW-space Y for k≥2 since the group[ΣkY,ΣkY]becomes abelian for k ≥ 2.However,it is reasonable for us to conjecture that there are lots of self-maps in this abelian group which are nontrivial rationally,but suspend to the trivial self-map of Σk+1Y. AcknowledgementThe author is grateful to the anonymous referees for their careful readings and many helpful suggestions that improved the quality of the paper. [1]Adams,J.F.,An example in homotopy theory,Proc.Camb.Phil.Soc.,53,1957,922–923. [2]Arkowitz,M.and Curjel,C.R.,Homotopy commutators of finite order(I),Quart.J.Math.Oxford,Ser.2,14,1963,213–219. [3]Bott,R.and Samelson,H.,On the Pontryagin product in spaces of paths,Comment.Math.Helv.,27,1953,320–337. [4]Bous field,A.K.and Kan,D.M.,Homotopy limits,completions and localizations,Lecture Notes Math.,304,1972. [5]Félix,Y.,Halperin,S.and Thomas,J.C.,Rational Homotopy Theory,GTM,205,Springer-Verlag,New York,2001. [6]Gray,B.I.,Spaces on the same n-type for all n,Topology,5,1966,241–243. [7]Hilton,P.J.,On the homotopy groups of the union of spheres,J.Lond.Math.Soc.,30(2),1955,154–172. [8]Lee,D.-W.,On the same n-type conjecture for the suspension of the in finite complex projective space,Proc.Amer.Math.Soc.,137(3),2009,1161–1168. [9]Lee,D.-W.,On the same n-type structure for the suspension of the Eilenberg-MacLane spaces,J.Pure Appl.Algebra,214,2010,2027–2032. [10]Lee,D.-W.,On the same n-type of the suspension of the in finite quaternionic projective space,J.Pure Appl.Algebra,217,2013,1325–1334. [11]McGibbon,C.A.and Møller,J.M.,On in finite dimensional spaces that are rationally equivalent to a bouquet of spheres,Proceedings of the 1990 Barcelona Conference on Algebraic Topology,Lecture Notes Math.,1509,1992,285–293. [12]McGibbon,C.A.and Steiner,R.,Some questions about the first derived functor of the inverse limit,J.Pure Appl.Algebra,103(3),1995,325–340. [13]Morisugi,K.,Projective elements in K-theory and self-maps of ΣCP∞,J.Math.Kyoto Univ.,38,1998,151–165. [14]Moriya,S.,The de Rham homotopy theory and differential graded category,Math.Z.,271,2012,961–1010. [15]Ravenel,D.C.,Nilpotence and periodicity in stable homotopy theory,Annals of Mathematics Studies,128,Princeton University Press,Princeton,1992. [16]Ruiz,F.G.,A note on residue formulas for the Euler class of sphere fibrations,Chin.Ann.Math.Ser.B.,32(4),2011,615–618. [17]Scheerer,H.,On rationalized H-and co-H-spaces with an appendix on decomposable H-and co-H-spaces,Manuscripta Math.,51,1984,63–87. [18]Scoville,N.A.,Lusternik-Schnirelmann category and the connectivity of X,Algebr.Geom.Topol.,12,2012,435–448. [19]Spanier,E.,Algebraic Topology,McGraw-Hill,New York,1966. [20]Whitehead,G.W.,Elements of Homotopy Theory,GTM,61,Springer-Verlag,New York,1978. [21]Wilkerson,C.W.,Classification of spaces of the same n-type for all n,Proc.Amer.Math.Soc.,60,1976,279–285.2 Homotopy Self-Equivalences of CW-Spaces
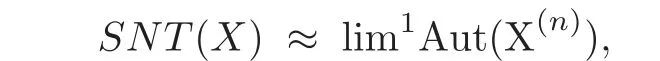


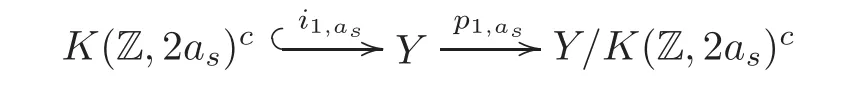

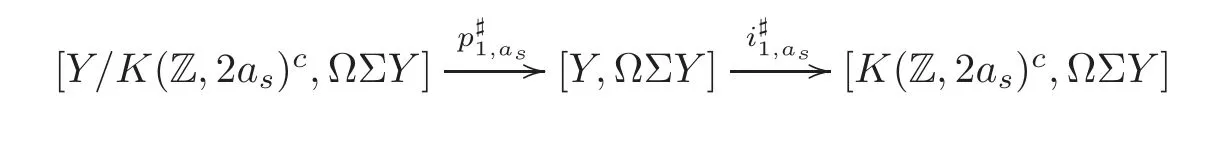
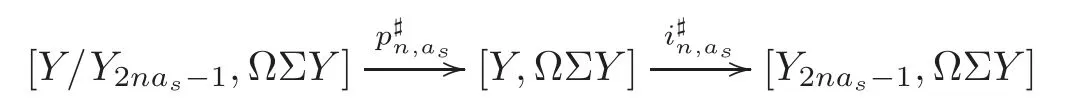
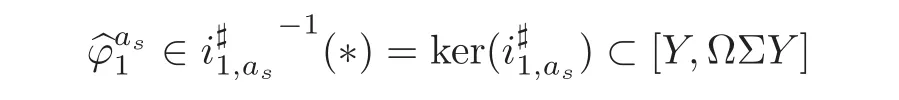
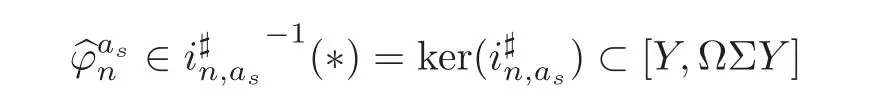
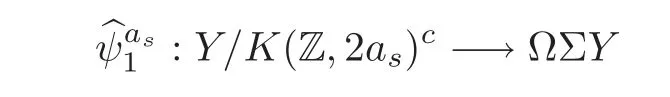



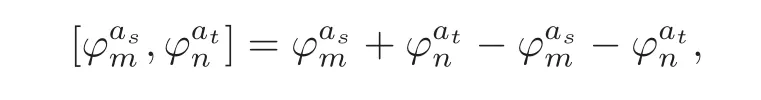
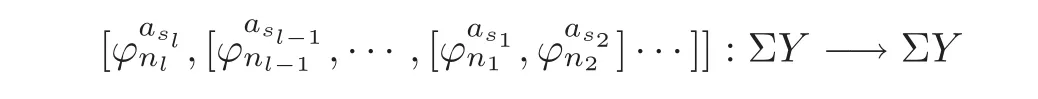


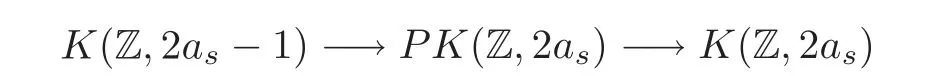
3 Proof of Theorem 1.1

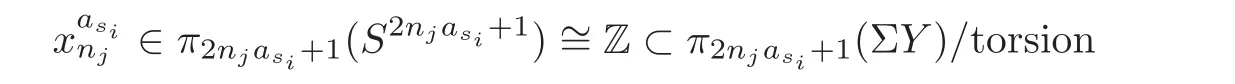

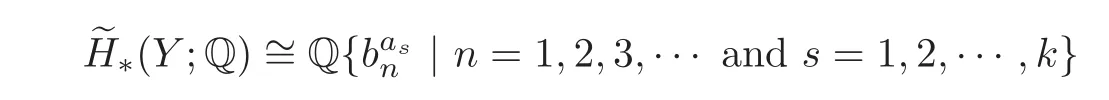



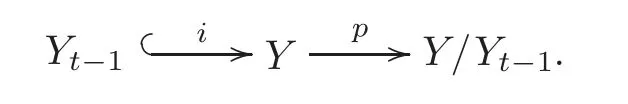
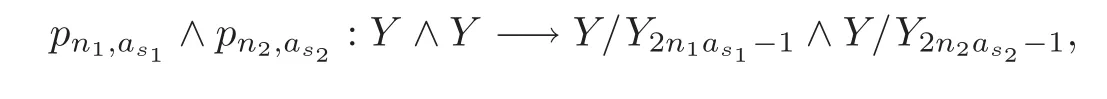
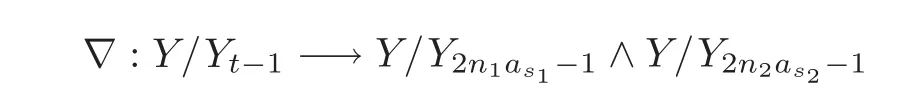
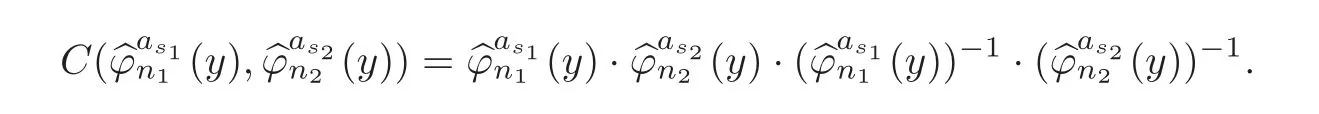
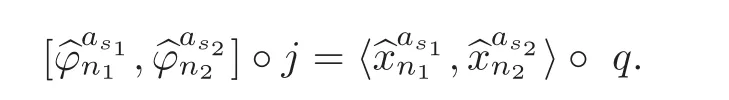
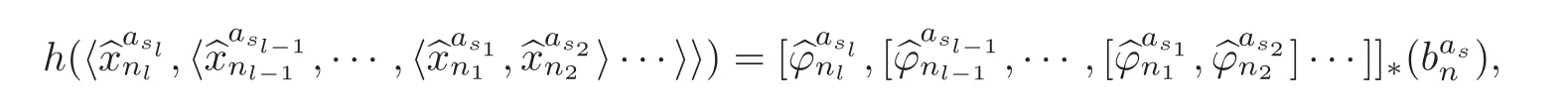




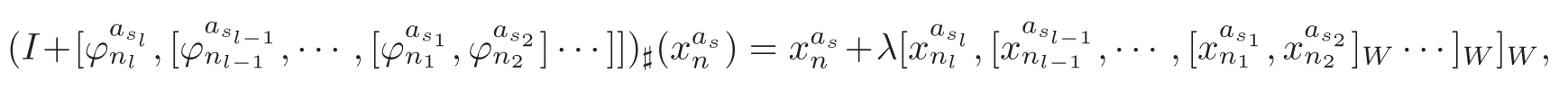
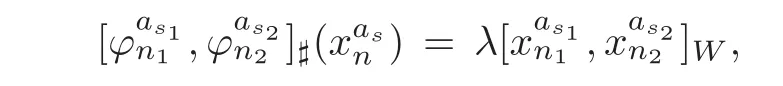

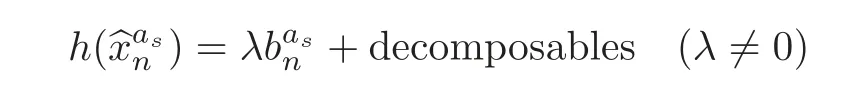
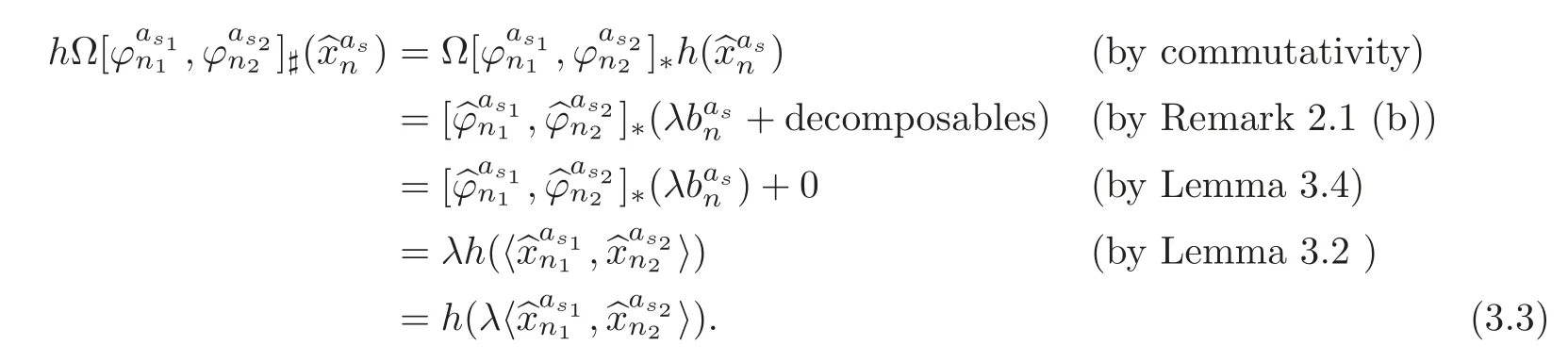
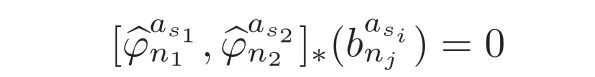

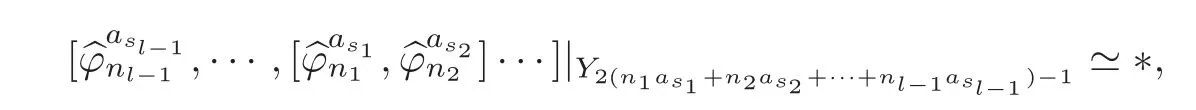

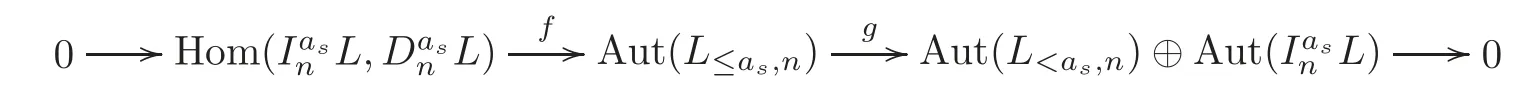
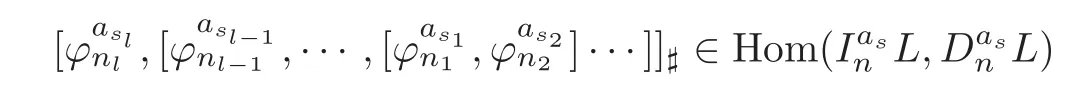


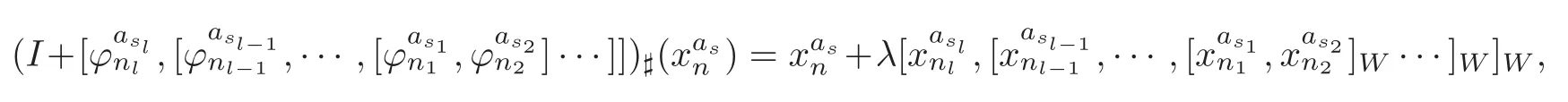
 Chinese Annals of Mathematics,Series B2016年6期
Chinese Annals of Mathematics,Series B2016年6期
