子的配分函数——物理意义与作用

刘国杰 史济斌(华东理工大学化学系，上海 200237)



子的配分函数
——物理意义与作用

刘国杰 史济斌*
(华东理工大学化学系，上海 200237)

摘要：讨论怎样理解子的配分函数的物理意义，以及它和系统的配分函数在计算热力学函数中的作用，指出它既不是系统的广延性质，也不是系统的强度性质，只是联系系统热力学函数与微观信息的纽带。

关键词：子的配分函数；正则配分函数；热力学函数；强度性质；广延性质

在独立子或近独立子系统的统计热力学中，有一个关键性的函数，称为子的配分函数， 只要已知这个函数，系统的一切热力学函数便随之确定。本文试图深入探讨这个函数的意义与作用。

1 子的配分函数的定义

子的配分函数的定义是：

子的配分函数也常定义为：

子的配分函X数还常表示成：

2 子的配分函数的物理意义

子的配分函数的物理意义可从两个角度来理解。

2.1从定义式的角度理解

2.2从Boltzmann能量分布定律理解

如果将子的配分函数按式(3)定义，则Boltzmann能量分布定律为：

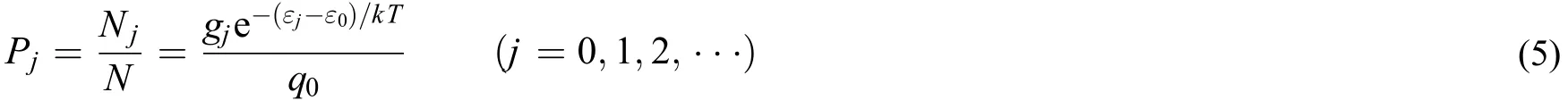
对于N个子构成的封闭系统，它反映了这些子在各能级上分配的整体特性[3]。

倘若只考虑子的热运动，则因子的平动、转动、振动的基态能级都是非简并的，，又也等于1，故由式(5)可得：

对于N指定的封闭系统，子的配分函数是子从基态能级逃逸程度的一种量度[4]。

物理意义的这种表述，虽只限于子的热运动，但却非常有意义。从这种表述能够进一步得到如下3点启示：

② 温度越高，子从基态能级逃逸到较高能级的程度越大，故子的配分函数的值是随温度升高而增大的。

③ 在相同的温度下，子的相邻能级的间隔越小，子越容易逃逸到较高能级，故值也越大，这就是说，平动子的最大，振子的最小，转子的介于其间。

因此，这种表述不仅简洁，而且具有启发性。

3 子的配分函数属于一个子所有

子的配分函数有一个重要的性质，称为配分函数的析因子性质。这个性质指出，如果子的能量是它的各种运动形式的能量之和，那么，子的配分函数则是相应运动形式的配分函数之积，即：

倘若子为非线型的多原子分子，则一般说来，子的配分函数当为：

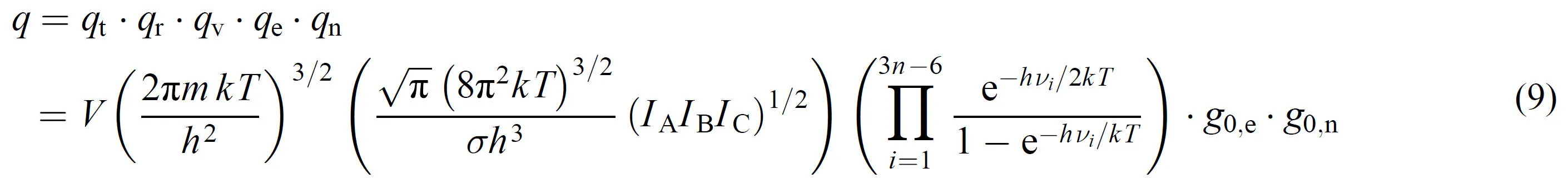
由此可见，子的配分函数除了包含系统的体积和温度外，还包含了独立子的质量m，对称数σ，3个主转动惯量、和， 3n – 6个谐振频率以及电子和核的基态能级简并度等重要的微观信息。其中温度总是以kT的形式出现，对于没有相互作用的独立子系统，它代表了一个子的能量。故只有在指定系统由N个独立子构成时，不但系统的微观性质确定，而且其宏观状态E、V、N也随之确定。由此可见，子的配分函数仅属于一个子所有。有的教材和教学参考书将子的配分函数计作，显然是不妥当的，因为这样表示便将q视为系统的性质。有的教材则进一步认为，式(9)正比于系统的体积V，而体积正比于物质的量，故离域子的配分函数应是系统的广延性质。同理，定域子的配分函数因与体积无关，则是系统的强度性质。本文认为，这种看法也是值得商榷的。式(9)中V虽与系统物质的量成正比，但却与子的配分函数是否是广延性质无关，在看了下文后，相信就会明白。总之，子的配分函数是属于一个子所有，而不是系统的属性。

4 子的配分函数与系统的热力学函数

根据正则系综原理，对于N、T、V指定的封闭系统，其热力学函数可由下列公式计算：

式中L为Avogadro常量，Z为系统的配分函数，也称正则配分函数。由于独立子系统中，子与子之间没有作用力，任一子并不因其他子的存在而改变其q的值，故系统的配分函数当为N个子的q之积，即：

式(15)仅适用于可辨别的定域子系统。对于离域子系统，因N个子是不可辨别的，其系统的配分函数应为：

现在，只要将式(15)和式(16)分别代入式(10)–式(14)，便可分别算得定域子和离域子系统的E、S、A、p和μ，并进而得到其他热力学函数。现以Helmholtz自由能为例，来表示计算的结果。

对于离域子系统，算得的A除与N有关，还与q/N有关。由于离域子的配分函数可表示为：

由此可见，离域子的配分函数(式(19))在代入式(18)后，它的体积V转变成了离域子系统的密度N/V，这是一个与物质的量无关的物理量。因此，由式(18)算得的离域子系统的A与式(9)或式(19)中的体积V无关，是一个仅正比于N的广延性质。这个结论也适用于其他广延性质。

由上述可见，虽然知道了子的配分函数就能算得系统的热力学函数，但是起决定作用的却是系统的配分函数，因为它除了包含系统的体积、温度和所有微观信息外，还包含了系统物质的量或N。那么，系统的配分函数是不是热力学变量呢？答案也是否定的。因为热力学变量分成两类，即强度性质和广延性质，前者与物质的量无关，后者与物质的量成正比。而由式(15)和式(16)可见，系统的配分函数虽与物质的量(即子数N)有关，但不成正比，这就是说，它既不是强度性质，也不是广延性质。因此，系统和子的配分函数都只能说是联系宏观热力学函数与微观信息的纽带。

参 考 文 献

[1]Tolman, R. C. The Principles of Statistical Mechanics; Oxford University Presss: Oxford, 1938.

[2]唐有祺. 统计力学及其在物理化学中的应用. 北京: 科学出版社, 1979.

[3]胡 英, 吕瑞东, 刘国杰, 黑恩成. 物理化学. 第5版. 北京: 高等教育出版社, 2007.

[4]Gasser, R. P. H.; Richards, W. G. 熵与能级. 曾 实, 译. 北京: 人民教育出版社, 1981.

• 自学之友•

The Physical Significance and the Role of the Molecular Partition Function

LIU Guo-Jie SHI Ji-Bin*
(School of Chemistry, East China University of Science and Technology, Shanghai 200237, P. R. China)

Abstract:We discussed the physical meaning of the molecular partition function, and the role of both the molecular partition function and the partition function of the system in the calculation of the thermodynamic properties. It was shown that the molecular partition function is neither an extensive property nor an intensive one, but only a tie to connect the thermodynamic properties with the microscopic information of the system.

Key Words:Molecular partition function; Canonical partition function; Thermodynamic function; Intensive property; Extensive property

*通讯作者，Email: shijb@ecust.edu.cn

doi:10.3866/pku.DXHX20160175www.dxhx.pku.edu.cn

中图分类号：G64；O6