回归分析法在坝基测压管水位预测中的应用

陆　健，杨子敬

(浙江乐清市淡溪水库管理所，浙江 乐清 325600)



回归分析法在坝基测压管水位预测中的应用

陆健，杨子敬

(浙江乐清市淡溪水库管理所，浙江 乐清 325600)

摘要：坝基水位是一个复杂的随机系统。根据坝基测压管水位与其影响因素之间存在的相关关系，运用回归分析理论和方法，建立了一个基于多元线性回归分析法的坝基测压管水位动态预测模型，并将该模型用于淡溪水库大坝坝基动态预测。预测结果表明预测精度较高，建立的模型较符合该研究区的实际情况。

关键词：坝基；动态预测；回归分析；水位；应用

0引言

淡溪水库坝址座落在淡溪镇石龙头村上游(E120°59′，N28°15′)，位置图见图1。在坝基的安全分析工作中,坝基水位的预测至关重要,坝基水位预测是大坝管理、评价和管理工作的基础。文章采用多元线性回归分析方法对研究区坝基水位进行动态预测,结果表明预测精度较高。

1回归分析模型

一元线性回归是一个主要影响因素作为自变量来解释因变量的变化，在现实问题研究中，因变量的变化往往受几个重要因素的影响，此时就需要用2个或2个以上的影响因素作为自变量来解释因变量的变化，这就是多元回归亦称多重回归。当多个自变量与因变量之间是线性关系时，所进行的回归分析就是多元性回归。 设y为因变量，x1，x2，……，xk为自变量，并且自变量与因变量之间为线性关系时，则多元线性回归模型为：

y=b0+b1x1+b2x2+…+bkxk+e

(1)

式中：b0为常数项，b1，b2……bk为回归系数，b1为x2,x3…xk固定时，x1每增加一个单位对y的效应，即x1对y的偏回归系数；同理b2为x1，x3…xk固定时，x2每增加一个单位对y的效应，即，x2对y的偏回归系数，等等。如果两个自变量x1,x2同一个因变量y呈线相关时，可用二元线性回归模型描述为：

可用二元线性回归模型描述为：

y=b0+b1x1+b2x2+e

(2)

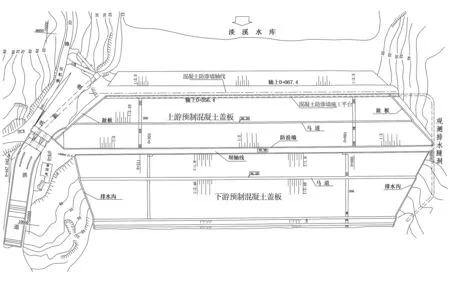
图1淡溪水库位置图

建立多元性回归模型时，为了保证回归模型具有优良的解释能力和预测效果，应首先注意自变量的选择，其准则是：

1)自变量对因变量必须有显著的影响，并呈密切的线性相关；

2)自变量与因变量之间的线性相关必须是真实的，而不是形式上的；

3)自变量之彰应具有一定的互斥性，即自变量之彰的相关程度不应高于自变量与因变量之因的相关程度；

4)自变量应具有完整的统计数据，其预测值容易确定。

多元性回归模型的参数估计，同一元线性回归方程一样，也是在要求误差平方和(∑e2)为最小的前提下，用最小二乘法求解参数。以二线性回归模型为例，求解回归参数的标准方程组为：

(3)

解此方程可求得b0,b1,b2的数值。亦可用下列矩阵法求得：

b=(x′x)-1×(x′y)

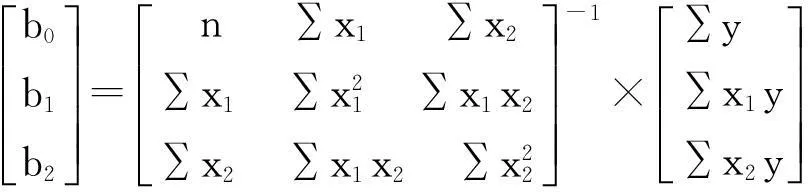
(4)

3坝基测压管水位回归统计分析

对本工程而言，下游水位无观测资料，且下游水位受水库放水影响较大，本次将水库放水期间的监测资料剔除后进行回归分析[1-2]。剩余管水位对降雨与库水位影响反应较灵敏，因此通过试算，采用下列的统计模式比较合适。

H=a0+a1h0+a2h1-3+a3h4-8+

a4h9-18+a5R0+a6R1-3+a7R4-8+

a8θ+a9θ2+a10θ3+a11ln(1+θ)

(5)

式中：H为测压管管水位；h0为观测日当天的水头，库水位m；hi-j为观测日前第i天到第j天的平均水头；R0为观测日当天的降雨量；Ri-j为观测日前第i天到第j天的平均降雨量；θ为观测日至正常观测起始日天数的1/100；ak(k=0～11)为待定系数。

考虑到前期测压管观测数据不稳定，下游情况变化较复杂，回归观测数据取2002年6月—2010年12月的资料进行回归分析。

根据以上回归方程选入因子，对水位、降雨量及时效分量进行偏相关分析，求得各分量的偏相关系数，其结果见表1。

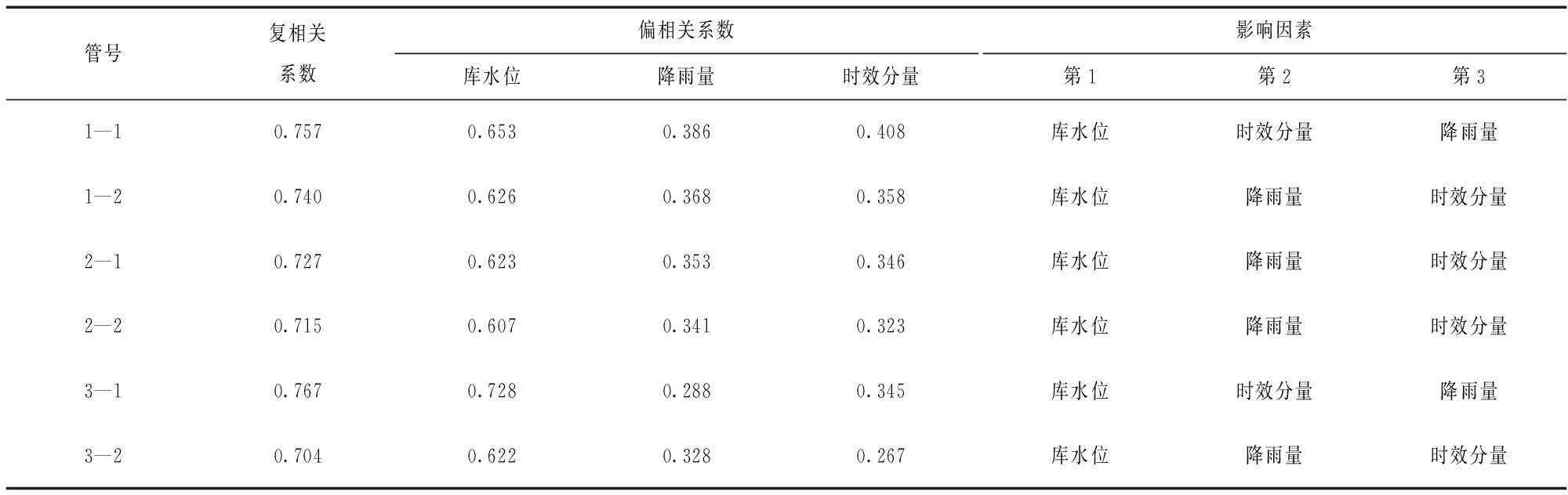
表1　测压管水位回归偏相关系数

由回归分析的图表分析结果如下：

1)各管水位均以库水位作为第1影响因素；降雨与时效的偏相关系数相近。

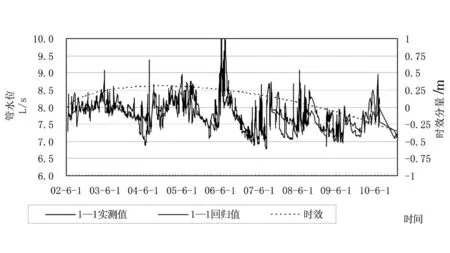
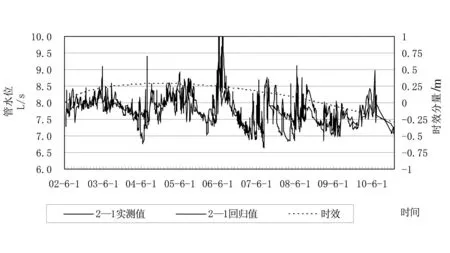
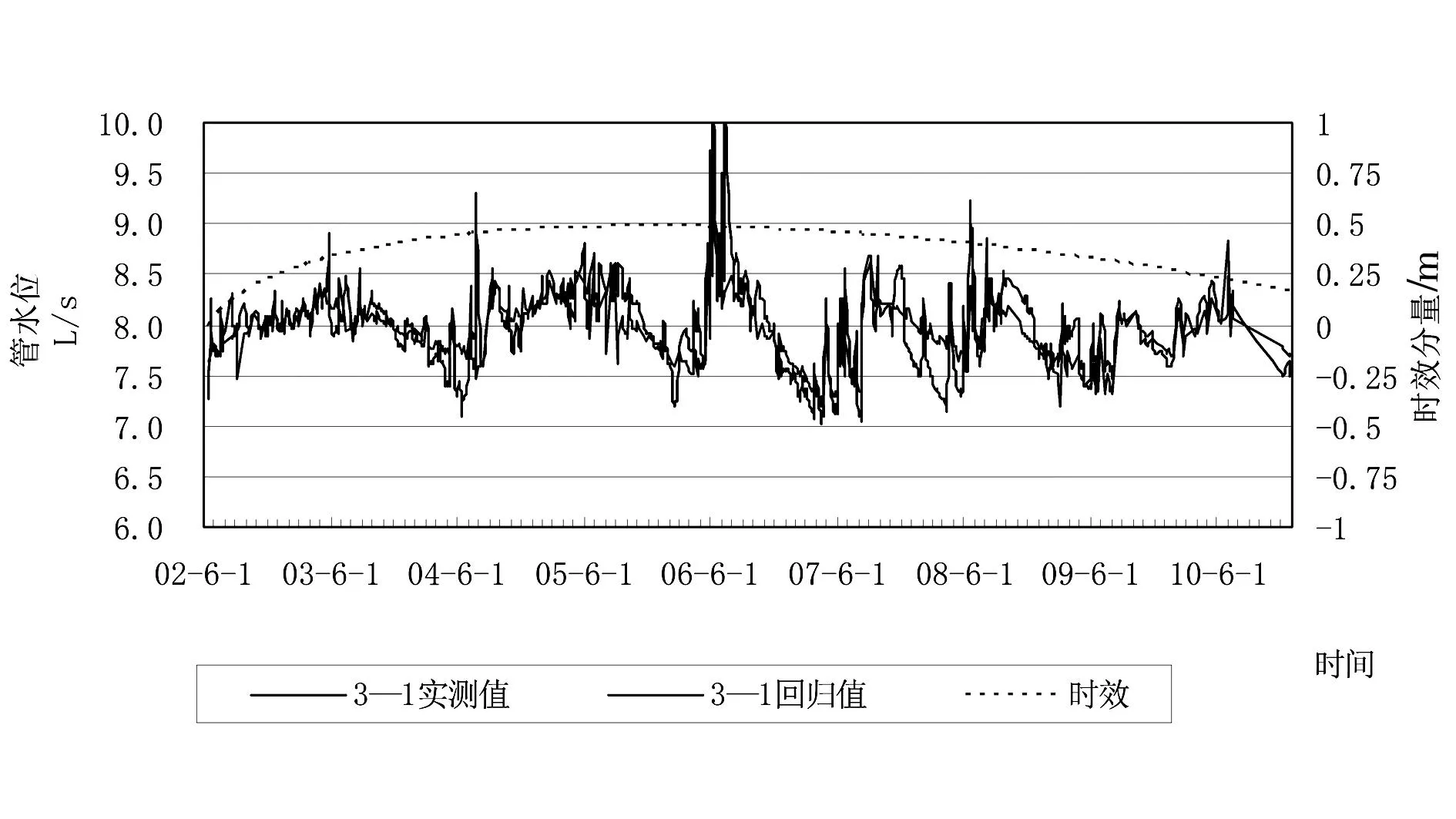
2)从各管的时效分量来看，3-1#测压管前期升高稍大，可能是由于大坝右侧防渗墙质量稍差，局部存在一些薄弱环节，在渗流作用下局部产生渗透变形所致。从2005年起，各测压管水位基本呈缓慢下降趋势，表明目前大坝坝基本防渗系统基本稳定，没有向不利方向转变。但日常仍应加强对坝基测压管水位的监测与分析，特别是3-1#测压管应更加注意。测压管水位实侧值和回归预测值的分析见表2与图2。

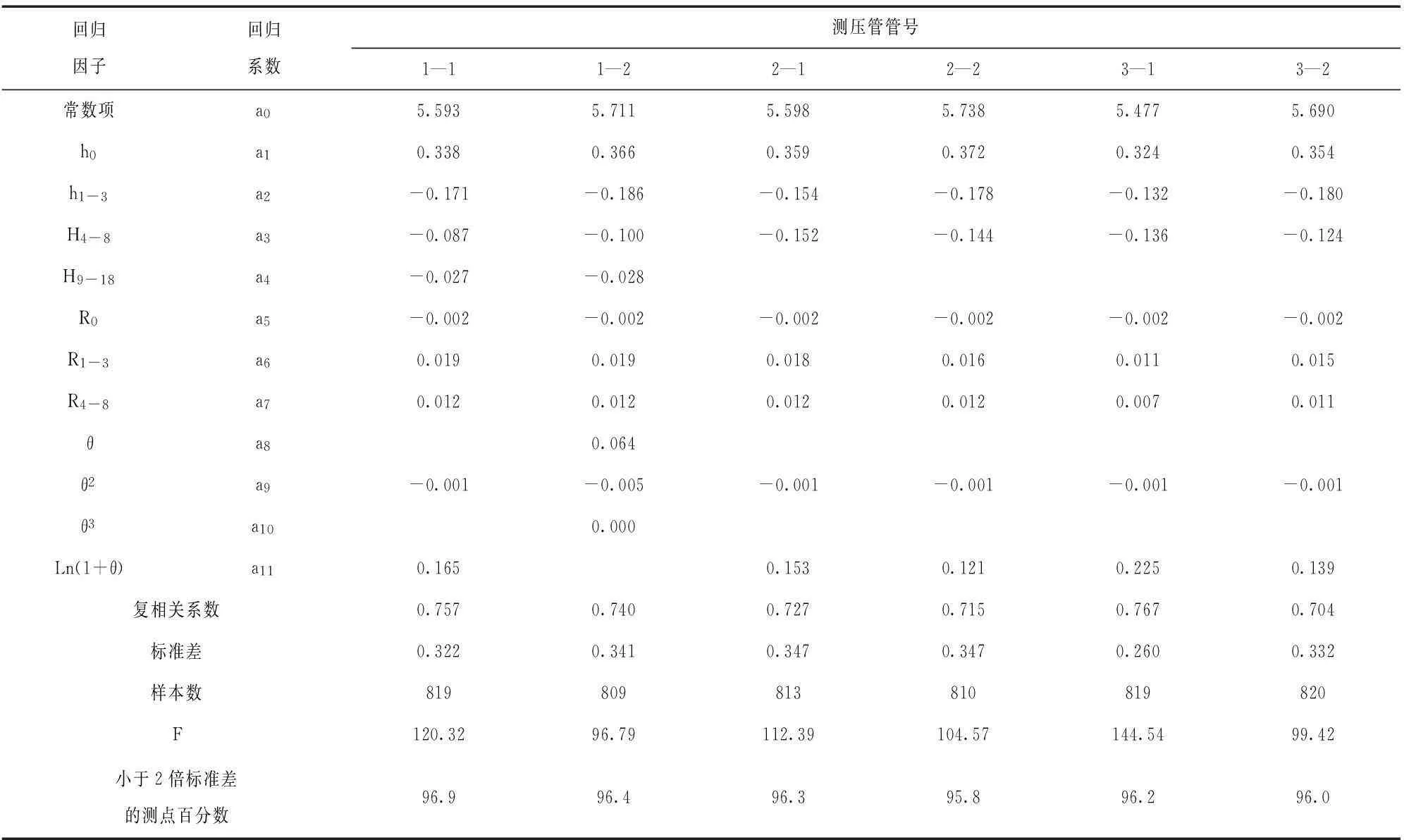
表2　测压管水位回归分析成果表

统计模型：H=a0+a1h0+a2h1-3+a3h4-8+a4h9-18+a5R0+a6R1-3+a7R4-8+a8θ+a9θ2+a10θ3+a11ln(1+θ)

4结论

通过坝基渗流监测资料统计分析，结合施工情况、现场情况与工程经验，对坝基渗流状态得到如下3点结论[3]：

1)除险加固后，各测压管平均水位为7.9m，管水位一般在7～9m变化，而除险加固前坝基测压管水位大多在10m以上，有时甚至达15m高程，因此坝基防渗墙防渗处理效果明显。

2)坝基各测压管之间水位差较小，坝基砂砾石透水性较强，坝基内的渗透比降较小，不会造成坝基渗透破坏。

3)大坝右岸防渗墙施工中曾多次出现塌孔、掉钻等问题，出现的问题虽进行了处理或论证，但仍会影响基础防渗墙的质量。大坝右侧测压管3-1#水位要高于其它测压管水位表明大坝基础防渗墙质量右岸比左岸差。同时日常仍应加强对坝基测压管水位的监测与分析，特别是3-1#测压管应更加注意。

参考文献：

[1]晏鄂川,王亮清,王初生.陆浑水库坝基水位观测资料分析[J].地质科技情报，2000，19(5)：59-63.

[2]吴喜定.陆浑水库简介[J] .人民黄河，1990(05)：10-11.

[3]刘杰.陆浑坝基运行现状安全评价[J] .人民黄河，1990(05)：21-24.

Application of Regression Analysis Method in Dam Foundation Piezometric Pipe Water Level Forecast

LU Jian and YANG Zi-jing

(Leqing Urban Danxi Reservoir Management Department，Leqing 325600,China)

Abstract：Water level of the dam foundation is a complex random system.In accordance with the correlation of dam foundation piezometric pipe water level and its influence factors，the regression analysis theory and method were used to set up a dynamic forecast model of dam foundation piezometric water level based on the multiple linear regression analysis method，and this model was used in the dynamic forecast for Danxi reservoir dam foundation.The forecasted results show that the accuracy forecasted is high and the model fits in with the facts of the study area.

Key words：dam foundation；dynamic forecast；regression analysis；water level；application

中图分类号：P332.3

文献标识码：B

[作者简介]陆健(1974-)，男，浙江乐清人，工程师；杨子敬(1980-)，男，浙江乐清人，工程师。

[收稿日期]2016-02-05

文章编号：1007-7596(2016)03-0110-04