负重屈伸运动对腰椎受力的有限元分析
吕永强,彭春政(鲁东大学 体育学院,山东 烟台 64025)
负重屈伸运动对腰椎受力的有限元分析
吕永强,彭春政
(鲁东大学 体育学院,山东 烟台 64025)
目的:量化人体从直立到前屈90°运动过程中腰段椎体、纤维环、髓核最大Von mises应力的变化规律。方法:利用已有的脊柱复合体三维有限元模型,采用有限元分析人体自重、外加负荷和肌肉力作用下,从直立到前屈90°腰部椎体的应力变化情况。结果:从直立到前屈90°运动过程中,随着前屈角度的增大,负重状态下腰部椎体的弯曲角度和整个椎体承受的载荷也随着增大,压力变化最敏感的是髓核;椎体皮质骨承受的最大Von mises应力值最大,椎弓根部是整个椎弓承受压力最大的区域;纤维环承受压力最大的区域在外侧部;随着弯曲角度的增大,作用于纤维环和髓核上的最大应力主要位于腰骶关节附近。结论:负重前屈运动中,通过增大脊柱的弯曲角度及重物靠近身体有利于减少肌肉的受力,避免运动损伤的产生;椎间盘、纤维环受力最大的区域位于腰骶关节附近,此处易发生腰部损伤。
腰椎;有限元;屈伸运动;负重
脊柱特别是腰段脊柱不但在日常生活中承受人体重力,而且在运动中起到减少冲击、缓冲震动的作用。2009年首届中国国际腰椎外科高峰论坛上,专家指出我国腰椎病患者已突破2亿;大约80%的成年人都有过腰痛病史,并且有不断上升的趋势。腰椎的稳定受肌肉、韧带、筋膜等多种因素的影响,任何一种因素在外界直接或者间接作用下遭受破坏时,都可能导致腰部功能障碍,从而引发腰部疼痛甚至形成伤残。流行病学调查显示:日常生活工作中反复屈伸运动特别是负重屈伸运动在某种程度上能引发肌肉和韧带损伤,从而导致腰部慢性劳损[1-4]。
为了更深入地了解人体运动过程中脊柱受力情况,国外学者采用基于肌肉最大力量与肌肉生理横断面积(PCSA)比的平方和为优化目标函数对人体屈伸运动过程中腰部肌肉力量进行预测[5];Kong等首次采用有限元分析方法对人体直立位和屈曲30°位腰部椎体、肌肉、韧带的受力进行分析[6]。到目前为止,负重状况下从直立位到屈曲90°腰椎受力情况的研究报道相对比较缺乏,而负重大幅度反复屈伸运动引起腰部慢性损伤的几率更大[7-10]。鉴于此,本研究对腰椎负重屈曲从直立位到弯曲90°4个不同姿势进行了有限元分析,探讨负重屈伸运动对腰椎受力的影响,为预防、减少和避免疲劳性损伤和疼痛的发生提供一定的理论依据。
1 研究对象与方法
1.1 研究对象
受试者为鲁东大学非体专业男生15名,自愿参加本测试,并无任何胸腰部肌肉损伤和胸腰背伤痛史。年龄、身高和体重平均标准差分为(20±3.16)岁、(1.76±5.74)m、(66.5±7.13)kg。
1.2 实验方法
采用测力台与红外线摄像机同步测试,受试者站在测力台上,听到实验员的口令开始在常速下负重25 kg完成从直立位到屈90°运动,工作过程尽量保持匀速。同步信号由测力台触发,当测力台接收到信号时开始测试数据,通过测力台的预留频道发出同步信号给VICON收集器。受试者需成功采集数据两次方可。
躯干屈伸过程中腰骶关节以及椎体间的相对运动是确定肌肉力量的关键,为了明确躯干从直立位到前屈90°整个运动过程中腰骶关节和椎体间的相对运动,采用在相应椎体棘突处贴Marker 的方法,Marker点黏贴的位置是:T1(胸1),T5,T10,T12,L1,L2,L3,L4,L5和S(骶骨)。
1.3 有限元模型建立和验证
选取其中一名年龄为22岁、身高为1.75 m、体重为65 kg的受试者为建模对象,建立躯干三维有限元模型(图1)。有限元模型的建立、材料参数的选择和验证在参考文献[11]中已具体论证。
每块肌肉的起、止点及PCSA值,都根据解剖学知识并且在专业解剖老师的指导下,采用一定体积的线直接连接完成。在研究中为了表现肌肉的真实形态,采用viapoint法对上部部分肌肉进行构建(胸腰部肌骨模型见图2)。
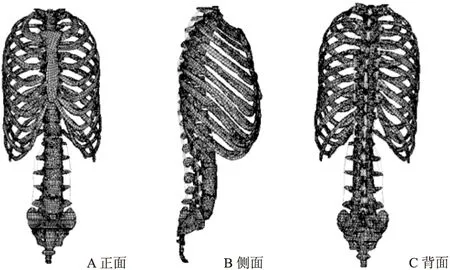
图1 整个有限元模型的网格图
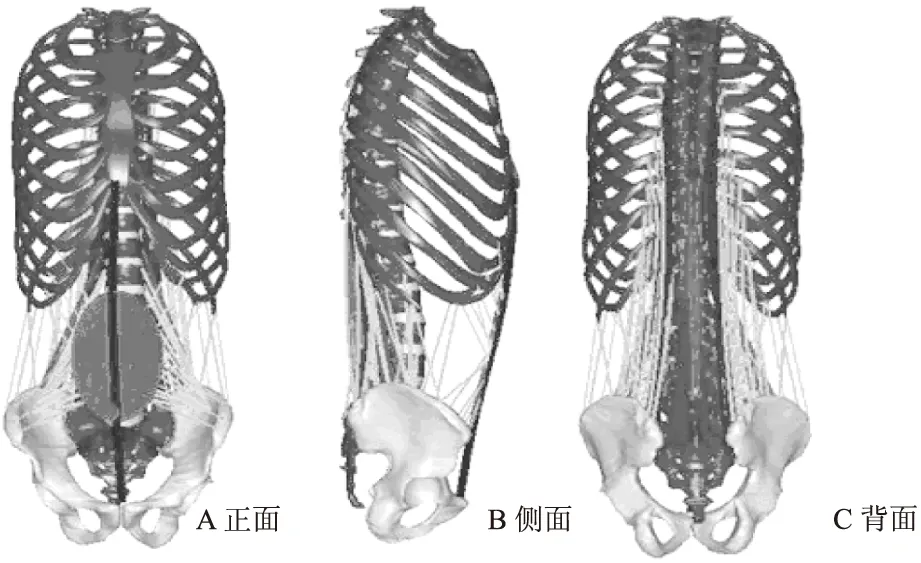
图2 人体中轴骨-肌系统图
1.4 加载条件和约束条件的限制
根据VICON解析的数据选取直立位、前屈30°、60°和90° 4个位相进行分析,假设整个运动过程为匀速运动,所受到的合外力为零,以肌肉应力平方和最小为目标函数,采用二次优化算法获得加载的肌肉力[12-13]。
1.4.1 运动过程力臂的计算 椎体相对运动的角度通过比较相应椎体在不同屈曲位置的角度来确定。人体屈曲运动时骨盆同时运动,因此整个脊柱围绕着髋臼转动。通过(1)式可算出躯干屈伸运动过程中腰骶贡献率(表1)以及相应椎体之间角度的改变关系,根据该改变关系可推算出脊柱前屈不同角度时的模型(图3),从而预测肌肉运动到某相位时到转动中心腰骶关节中心点的力臂值。
(1)

表1 弯腰过程中腰骶贡献比率及相应椎体间角度的变化
根据空间解析几何原理可知:假设直线的方向向量为s={m,n,p},M0为直线L外任意一点,M是直线L上任意一点,通过式(2)可求出点M0到直线L距离:
(2)
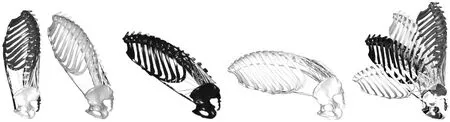
图3 前屈不同角度时的肌肉力线图
通过Matlab中的函数:
d=norm(cross(M0-M,s))/norm(s)
(3)
躯干负重从直立位到前屈90° 4个位相绕各自转动中心的力臂值如表2所示。
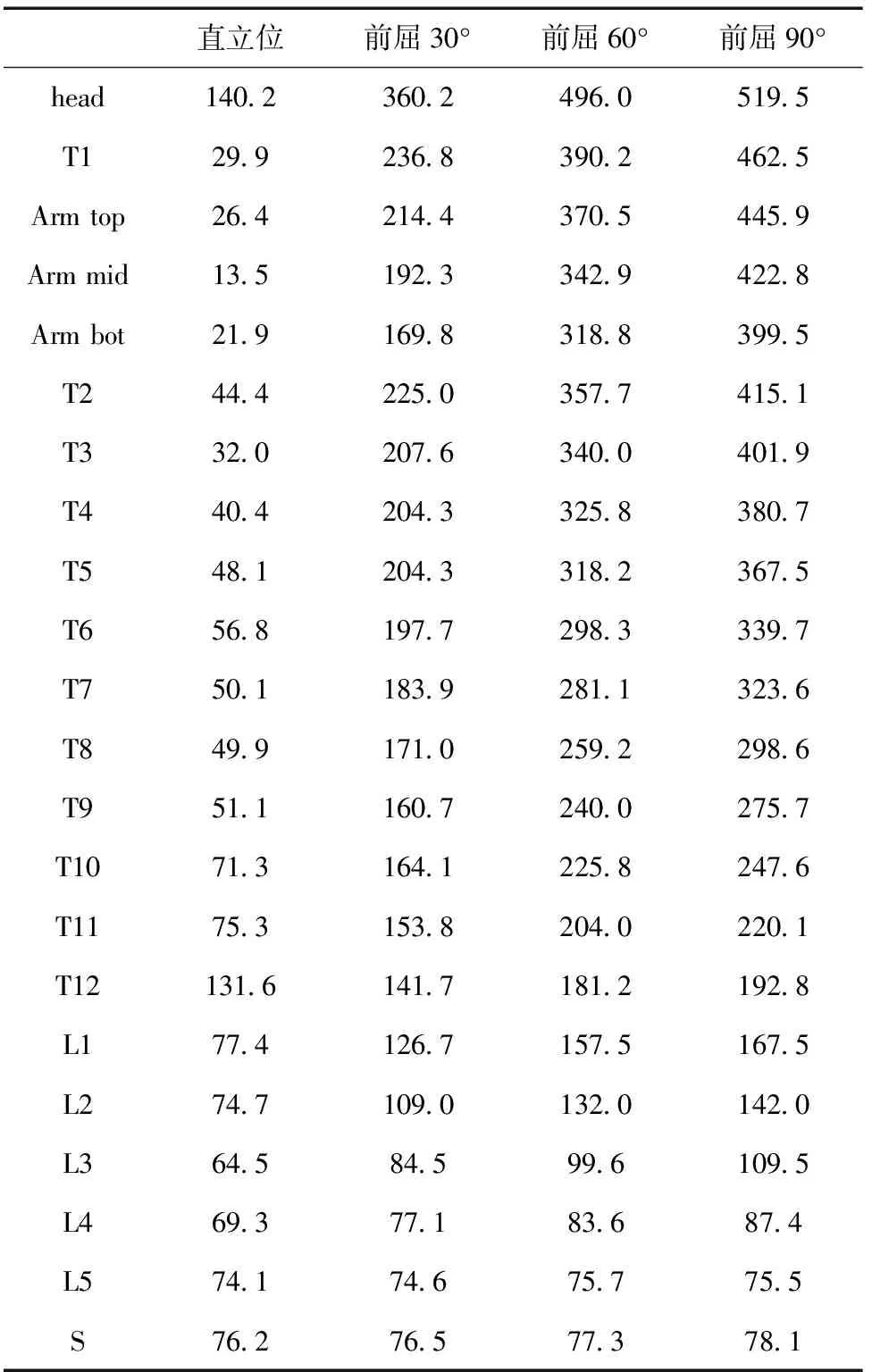
表2 躯干从直立位到前屈90° 4个位相分布质量到质心的力臂值(单位:mm)
1.4.2 肌肉力量预测 假设在整个弯腰搬物过程中基本上是匀速运动,则可近似地认为在任一运动时刻所受到的合力为零,则:
(4)
(5)

约束条件:
Fi≥0
Fi-σPCSAi≤0
(6)
优化目标函数[8]:
(7)
对式(4)(5)(6)(7)可以转化为如下的二次规划问题来求解:
s.t.Ax≤b,Aeq·x=beq,lb≤x≤ub
(8)
(8)式中采用C表示n维列向量,b代表m维列向量,H表示n阶对称正定矩阵,A表示m×n矩阵,A的秩为m,x∈En。由于不能直接采用消元法和Lagrange方法对公式(8)进行直接求解,因此使用起作用集方法对公式(8)进行求解。每次迭代运算,都采用已知的可行点为起点,并把该点的起作用约束设为等式约束,并在此约束力下进行极小化目标函数f(x)运算,具体算法参照陈宝林的研究[13]。
根据上述的计算方法,采用Matlab7.1工程计算软件中的优化模块编程,实现对肌肉力的预测。
1.4.3 加载条件和约束条件的设定 脊柱从直立位到前屈90°,长肌、棘肌、腰方肌、髂肋肌、腹直肌、腹外斜肌、腹内斜肌等肌肉都参与运动,共计179条肌肉束,采用局部坐标系下节点对所有参与运动的肌肉力进行加载(图4)。
人体自身的重量以及质心位置通过称重和图像解析法获得,据我国成年人人体质心的国家标准(GB/T17245-1998)确定人体各环节重量占整个人体重量的百分比以及人体各环节质心相对位置,外加载荷和人体各节段力量通过质量单元与相应椎体上的节点耦合。

注: 箭头代表179条肌束的肌肉力,三角形代表耦合,三角形下的雪花形表示人体的分布质点载荷,骶骨上的区域代表纵向位移约束。
图4 人体胸腰部的力学边界条件加载
2 有限元分析结果
2.1 有无载荷作用下矢状面内椎体中心连线的位移变化
从图5可以观察到施加载荷和未加载荷时,胸部脊柱弯曲角度都随着身体前屈角度的增大而增大;25 kg载荷时腰部矢状面屈曲的角度要大于无载荷时。
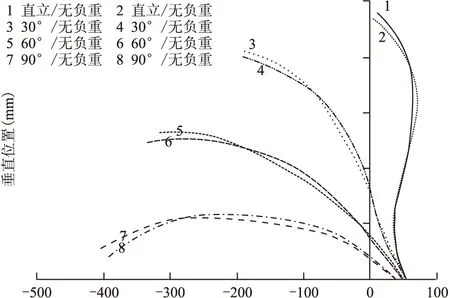
图5 有无载荷作用下脊柱椎体中心连线矢状面的位移
2.2 载荷作用下腰椎椎体受力的有限元分析
载荷作用下腰椎椎体不同部位所承受的载荷也具有一定的差异性,皮质骨、松质骨和椎体后部的Von mises应力分别如图6、图7和图8所示。在外载荷和身体自身重量的作用下,整个腰骶关节部椎体的受力由上而下都是逐渐增大,腰骶关节附近椎体皮质骨上的Von mises应力最大,前后面应力是腰椎应力的主要集中区域。直立位时,最大Von mises应力为25.728 MPa,随着人体屈曲角度的增大,腰椎椎体皮质骨的Von mises应力逐渐增大;当身体前屈90°时,最大应力值达到45.124 Mpa,约是直立位置时的1.75倍。
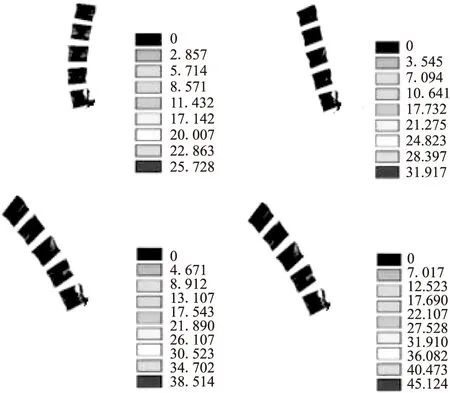
图6 负重状态下腰椎椎体皮质骨Von mises应力图
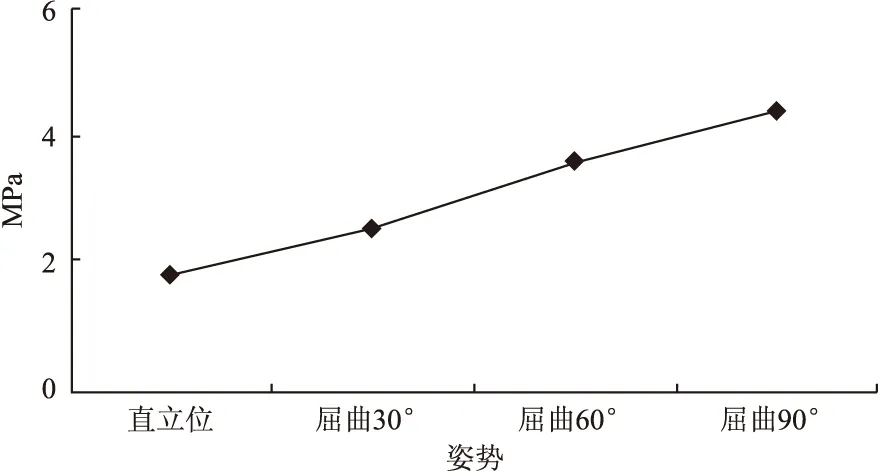
图7 负重状态下L5椎体松质骨的最大Von mises应力图
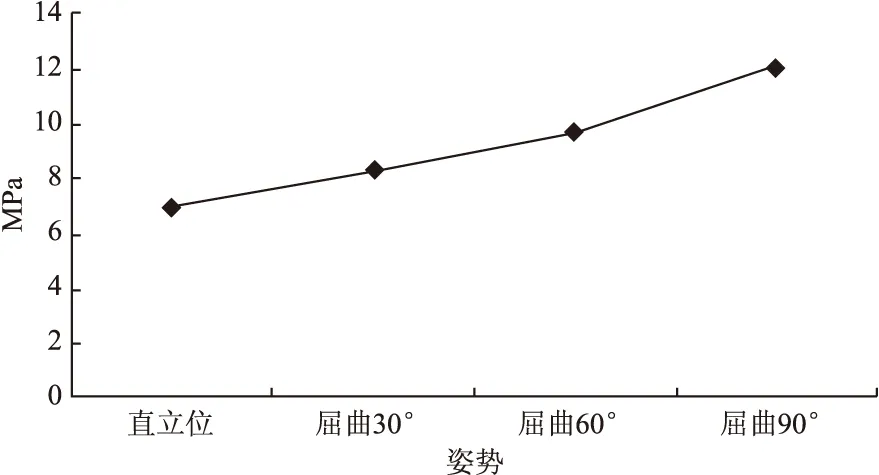
图8 负重状态下L5椎体后部结构最大Von mises应力图
整个运动过程中,松质骨的最大Von mises应力明显小于皮质骨,直立位最大Von mises应力只有1.89Mpa,在前屈90°时为4.41 Mpa。椎体后部椎体与椎板相连的椎弓根是应力集中的主要区域,该处最大Von mises应力约为松质骨最大Von mises应力的3倍。
2.3 负重状态下椎间盘应力分布的有限元分析
图9显示,从直立到前屈30°,纤维环的最大Von mises应力增大不明显;随着前屈角度的继续增大,纤维环的最大Von mises应力开始明显增加,60°时为26.073 Mpa,到达90°时达到38.68 Mpa,约是直立位时的2.65倍。图10显示,在整个运动过程中髓核承受的最大Von mises应力相对较小,但前屈角度对髓核受力影响较明显,直立位置时最大Von mises应力为0.445 Mpa,前屈30°时最大应力是直立位置时的3.44倍,到90°时增加到3.753 Mpa,增加到8.4倍多;腰骶关节连接处是整个腰部脊柱受力最大区域。
3 讨论与分析
以往对腰椎的研究中虽然也涉及到人体动力学计算及考虑肌肉力的作用,但只有上海交大王成韬教授带领的团队建立整个人体胸腰骶的模型,而整个胸腰骶实体模型的建立对研究人体脊柱大范围的运动具有非常重要的作用。因此本研究在建立整个人体胸腰骶实体模型的基础上,基于二次平方最小化的方法计算出肌肉力量作为加载条件,对腰部受力特别是第五腰椎受力进行有限元分析[7-9]。
通过建立一个简化的L1-S1有限元模型和较为详细的L1-S1非线性三维有限元模型,国外学者计算出直立位时人体腹部和背部肌肉的肌肉力。随着外加负荷的增加,脊柱主要通过减少前突和增大脊柱腰部弯曲角度减少在中立位时对肌肉的作用力,与本研究的结果基本一致[14-16]。从直立到前屈90°运动过程中,无负载荷作用下整个脊柱在矢状面的弯曲角度明显增大。矢状面内腰部脊椎弯曲角度的增大可有效地增加肌肉到腰骶关节的力臂,减少外载荷的力臂值,根据杠杆平衡原理有利于减少对肌肉的作用力。负重时,腰部脊柱的弯曲度比无负荷明显增大,说明人体可通过这种代偿性动作减少对肌肉的作用力,避免运动损伤的产生。
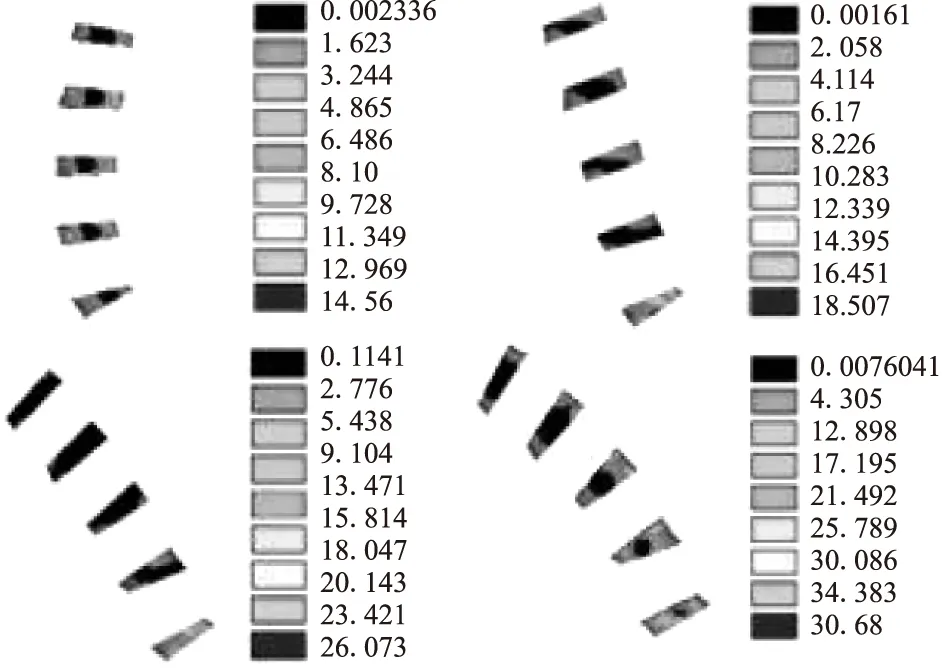
图9 纤维环的应力分布云图

图10 髓核的应力分布云图
椎骨主要由骨松质组成,表层密质较薄,由前方的椎体与后方的椎弓两部分组成。椎体与椎弓构成椎孔,内容脊髓及其被膜等。在整个运动过程中,随着身体前屈角度的增加,椎体骨组织的应力也随之增大。腰椎椎体中皮质骨承受的最大载荷明显大于松质骨,其主要原因是由椎体皮质骨和松质骨的力学性能差异造成的(椎体皮质的弹性模型远远大于松质骨的弹性模型),这与Wolff定律一致。腰椎和骶椎椎体后部是最大Von mises应力值集中出现的区域[17-18]。椎弓根部在解剖学上是椎体和椎弓连接处比较细小的区域,本研究中发现该部位是整个椎体后部应力主要集中区域,此处反复承受较大载荷作用时容易引发椎弓根部骨结构组织的变形,造成椎间孔形态和结构的变异,从而造成对通过脊神经和血管的挤压,容易导致下肢病变的发生[19]。
椎间盘由纤维环和髓核两部分组成。研究中发现,整个运动过程中,整个纤维环所承受的最大Von mises应力区域位于其后外侧,以往的研究也发现最大张力总是出现在纤维环后侧的内层纤维[20-21]。因此,当人体承受较大载荷时,纤维环的破裂多发生在此处。纤维环结构一旦遭到破坏,不但使髓核可靠的固定结构失去,而且由于纤维环结构破裂部位分担负荷能力的减小,导致髓核内部主要应力的增加,从而加重髓核疝出。研究中还发现随着前屈角度的增大,腰骶关节连接处的纤维环所承受的最大Von mises应力明显增大。提示在前屈运动时,当前屈角度较大时纤维环承受的载荷增大,此位置时纤维环更容易受到损伤,引发腰痛症状的产生。临床也证实,腰骶关节处是腰痛的好发部位。
国外学者对人体直立位和前屈10°、20°、30° 4个位相腹部和背部主要肌肉受力进行研究,发现通过实验直接测试的数值约比理论计算值大30%~40%;采用内置传感器对人体前屈30°无负荷和手持10 kg载荷时髓核内部压力进行测试,其最大压力分别是直立位的360%和430%[22-23]。本研究中负重状态下前屈角度为30°时最大应力是直立位置时的3.44倍。二者中间的差异可能是由采取的分析方法不同造成的,但二者的研究都发现身体姿势的改变对髓核受力影响非常明显。随着前屈角度的增大,髓核的最大应力增加更加明显,前屈90°时的最大应力约是直立姿势时的8.5倍,说明运动过程髓核所受的应力对前屈角度比较敏感。如果髓核在大负荷作用下长时间做屈伸运动,当身体前屈时,髓核压力异常增大会导致髓核周围的纤维环破裂引发髓核疝导致损伤的产生,而纤维环后部本身就是应力比较大的部位。因此此部位更易发生损伤,从而导致髓核从后部突出压迫神经,引发疼痛。
4 结论
负重状态下,从直立到前屈90°,脊柱可通过增大弯曲角度减少对肌肉的作用力;椎体的皮质骨承受的载荷最大,椎弓根部是整个椎弓受力最大区域;纤维环的最大受力区域位于后外侧,前屈角度对髓核受力影响较明显。整个运动过程中,腰骶关节连接处的纤维环所承受的最大Von mises应力最大,人体屈曲运动时腰骶关节处是最易发生损伤的部位。
[1] Perie D,Aubin CE,Lacroix M,et al.Biomechanical modelling of orthotic treatment of the scoliotic spine including a detailed representation of the brace-torso interface[J].Medical and Biological Engineering and Computing,2004,42(3):339-344.
[2]Guo LX,Teo EC.Prediction of the modal characteristics of the human spine at resonant frequency using finite element models[J].Proc Inst Mech Eng H,2005,219(4):277-284.
[3]Zhong ZC,Wei SH,Wang JP,et al.Finite element analysis of the lumbar spine with a new cage using a topology optimization method[J].Med Eng Phys,2006,28(1):90-98.
[4]Rohlmann A,Neller S,Bergmann G,et al.Effect of an internal fixator and a bone graft on intersegmental spinal motion and intradiscal pressure in the adjacent regions[J].Eur Spine J,2001,10(4):301-308.
[5]Arjmand N,Shirazi-Adl A.Model and in vivo studies on human trunk load partitioning and stability in isometric forward flexions[J].Journal of Biomechanics,2006,39(3):510-521.
[6]Kong WZ,Goel VK.Ability of the finite element models to predict response of the human spine to sinusoidal vertical vibration[J].Spine,2003,28(17):1961-1967.
[7]Wen-Zhong Nie,Ming Ye ,Zhen-Yu Wang.Infinite models in scoliosis-a review of literature and personal experiences[J].Biomedizinische Technik / Biomedical Engineering,2008,53(4):1645-1651.
[8]Nie WZ,Ye M,Liu ZD,et al.The patient-specific brace design and biomechanical analysis of adolescent idiopathic scoliosis[J].Biomech Eng,2009,131(4):41-47
[9]聂文忠,张绍祥,王成焘.基于冷冻切片的人体腰椎三维有限元模型[J].医用生物力学,2007,22(3):163-168
[10]聂文忠.脊柱胸腰部的生物力学建模与应用研究—中国力学虚拟人的基本问题初探[D].上海:上海交通大学,2009.
[11]彭春政,张胜年,陆爱云.人体躯干骨骼-肌肉-韧带结构三维有限元模型的建立和验证[J].中国运动医学杂志,2010(6):702-705.
[12]Winter J M.Biomechanics and motor control of human movement[M].NY:John Wiley ﹠Sons,2009.
[13]陈宝林.最优化理论与算法[M].北京:清华大学出版社,2000.
[14]Zhang SX,Heng PA,Liu ZJ,et al.The Chinese visible human(CVH) datasets incorporate technical and imaging advances on earlier digital humans[J].Journal of Anatomy,2004(3):165-173.
[15]Zander T,Rohlmann A,Calisse J,et al.Estimation of muscle forces in the lumbar spine during upper-body inclination[J].Clini Biomech,2001,16(5):S73-80.
[16]Pope MH,Wilder DG,Matteri RE,et al.Experimental measurements of vertebral motion under load[J].Orthop Clini Nor Ameri,1977,8(1):155-167.
[17]Roy-Camille RMD,Saillant GMD,Mazel CMD.Internal fixation of the lumbar spine with pedicle screw plating[J].Clin Orthop Relat Res,1986,203:7-17.
[18]Morgan EF,Bayraktar HH,Keaveny TM.Trabecular bone modulus-density relationships depend on anatomic site[J].J Biomech,2003,36(7):897-904.
[19]Keller TS.Predicting the compressive mechanical behavior of bone[J].J Biomech,1994,27(9):1159-1168.
[20]Rohlmann A,Neller S,Bergmann G,et al.Effect of an internal fixator and a bone graft on intersegmental spinal motion and intradiscal pressure in the adjacent regions[J].Eur Spine J,2001(10):301-308.
[21]Zander T,Rohlmann A,Calisse J,et al.Estimation of muscle forces in the lumbar spine during upper-body inclination[J].Clini Biomech,2001,16(4):S73-S80.
[22]Panjabi MM,Greenstein G,Duranceau J,et al.Three-dimensional quantitative morphology of lumbar spinal ligaments[J].J Spinal Disor,1991,4(1):54-62.
[23]Markolf KL.Deformation of the thoracolumbar intervertebral joints in response to external loads:a biomechanical study using autopsy material[J].J Bone Joi Surge-Seri A,1997,54(3):511-533.
责任编辑:乔艳春
Finite Element Analysis about Lumbar Vertebra Stress of Flexion and Extension Movement with Loading
LÜ Yongqiang,PENG Chunzheng
(P.E. Department,Ludong University,Yantai 264025,Shandong,China)
Objective:To quantify the variations in lumbar vertebral,fibrous ring and the nucleus pulposus the maximum Von Mises stress form erection to flexion of 90° in sagittal.Methods:Using the spine finite element model to analyze the stress change from erection to flexion of 90° by taking human body weight,external load and muscle forces into account with finite element method.Results:The bend angle and the stress of lumbar vertebra both increase with increasing flexion angle form erection to flexion of 90°.The nucleus pulposus pressure was changed most sensitively.The maximum Von Mises stress of vertebral body was in cortical bone and the vertebral arch root was the area of the whole vertebral arch under maximum press.The area under maximum press of fiber ring was in the lateral part.With the bending angle increases,the maximum stress under fiber ring and lumbosacral was in the nearby of lumbosacral joint.Conclusion:Through increasing curvature of the spine and heavy objects close to body was beneficial to reduce muscle force and avoid sports injury in the movement of flexion with load.The area under press of intervertebral disc and fibrous ring was near lumbosacral joint and leads to the waist injure easily.
lumbar vertebra;finite element;flexion and extension;loading
2015-10-16;
2015-11-26
吕永强(1980—),男,讲师,硕士,主要研究方向为运动人体科学。
G804.63
A
1004-0560(2016)02-0092-06
◀运动人体科学

