用于降低计算复杂度的双相位因子PTS

冯卓明，周隆龙（华中科技大学光学与电子信息学院，武汉430074）

用于降低计算复杂度的双相位因子PTS

冯卓明，周隆龙
（华中科技大学光学与电子信息学院，武汉430074）

摘要：为降低OFDM系统的功率峰均比，提出一种新的PTS方法——双相位因子PTS（DP-PTS）。依次介绍了PTS、IPTS和DP-PTS方法的原理，并对3种方法进行了仿真实验，对比了3种方法的峰均比性能和计算复杂度。

关键词：OFDM；功率峰均比；部分传输序列；DP-PTS；IPTS

0　引言

正交频分复用（OFDM）是一种多载波调制技术，具有子载波间干扰小、频谱利用率高和可以有效抑制多径衰落等优点，但也存在高峰均比（Peak to Average Power Ratio，PAPR）的缺点。由于OFDM采用多载波技术，输出是多个子信道信号的叠加，当多个信号相位一致时，叠加的瞬时功率会远大于平均功率，从而导致较大的PAPR，而峰值功率过高，会引起信号失真。

降低PAPR的方法有很多，最简单有效的是限幅法[1]，但该方法在减小PAPR时会产生信号畸变。编码法[2～4]利用编码产生了不同码组，把消息信号映射到PAPR较小的码组上，降低了信息速率。选择性映射（SLM）[5]和部分传输序列[6～9]（PTS）以增加边带信息和提高计算复杂度为代价降低了信号的PAPR。其中SLM是把输入的数据与多个相位因子相乘，经傅里叶逆变换（IFFT）后选择PAPR最小的序列。PTS是把输入数据分为N个互不相交的子块，分别进行IFFT变换后，每个子块乘以一个相位因子，通过相位因子最优化来降低PAPR。与SLM相比，在计算复杂度相同的情况下，PTS展现出更好的性能，但也增加了相位因子的长度。为此，本文提出一种新的PTS方法——双相位因子PTS(Dual Phase PTS，DP-PTS)。

1　OFDM系统和PTS技术

1.1OFDM系统

在OFDM系统中，长度为N的调制信号{Xn，n=0，1，……，N-1}经过N点的IFFT运算后得到的输出信号表示为：

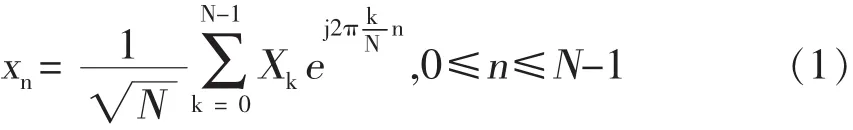
其中，N为子载波数，n表示一个OFDM符号周期内的第n个采样值。PAPR是指OFDM符号的峰值功率和该符号平均功率的比值，定义为：

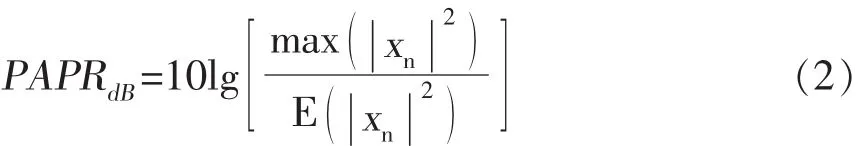
1.2PTS方法

PTS最早由S.H.Muller和J.B.Huber在文献[6]中提出，其基本思想是将N个符号的输入数据X=[x1，x2，……，xV]分割成V个不相交的子块X1、X2、……、XV,其中Xi=[0,……,0, xi,0,……,0]T是长度为N的子块。

PTS技术框图如图1所示，PTS把每一个分割后的子块乘以一个相应的复相位因子bv=ejφv，v=1,2，...，V,通过搜索算法，对相位因子进行优化，选择最佳的相位因子集合。最小PAPR向量的时域信号可以表示为：

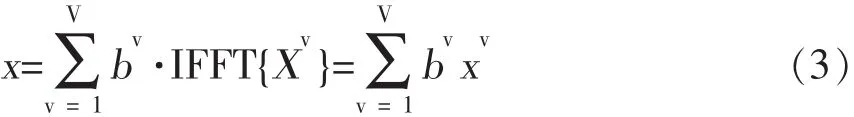
其中，bv为优化后的相位因子。理论上bv可以在[0,2π）之间任意取值，但为了降低搜索复杂度，bv一般在一个离散的相位集合中取值，常用的是{1，-1，j，-j}。若bv在W个相位因子中搜索最佳相位因子，则对于每一个数据块PTS技术需要V次IFFT运算和log2WV比特的边带信息。

1.3IPTS方法

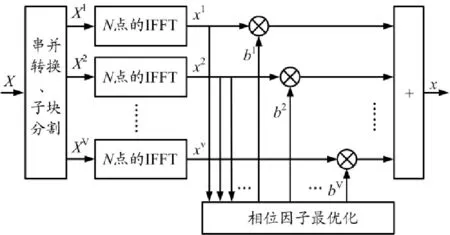
图1　PTS技术框图

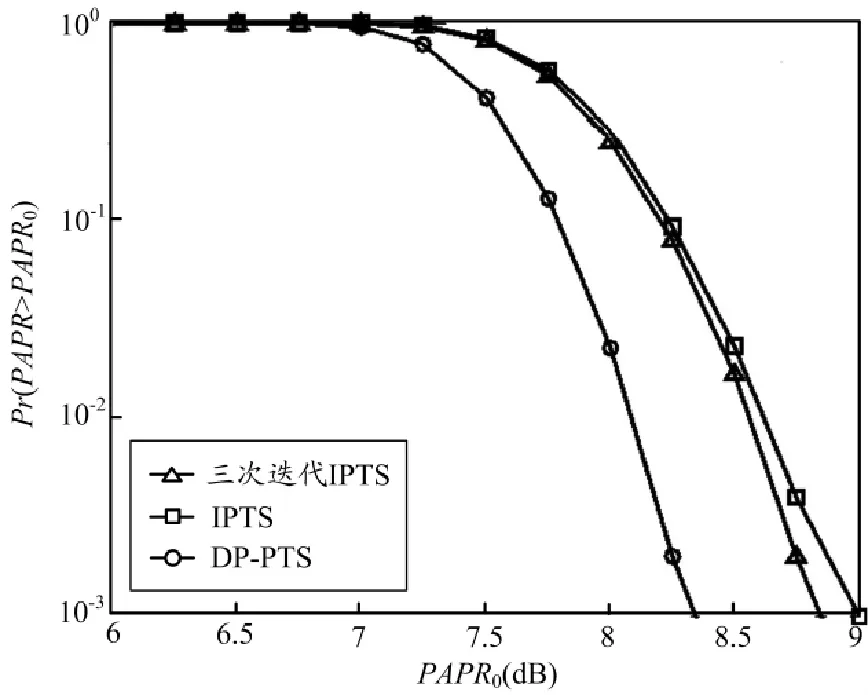
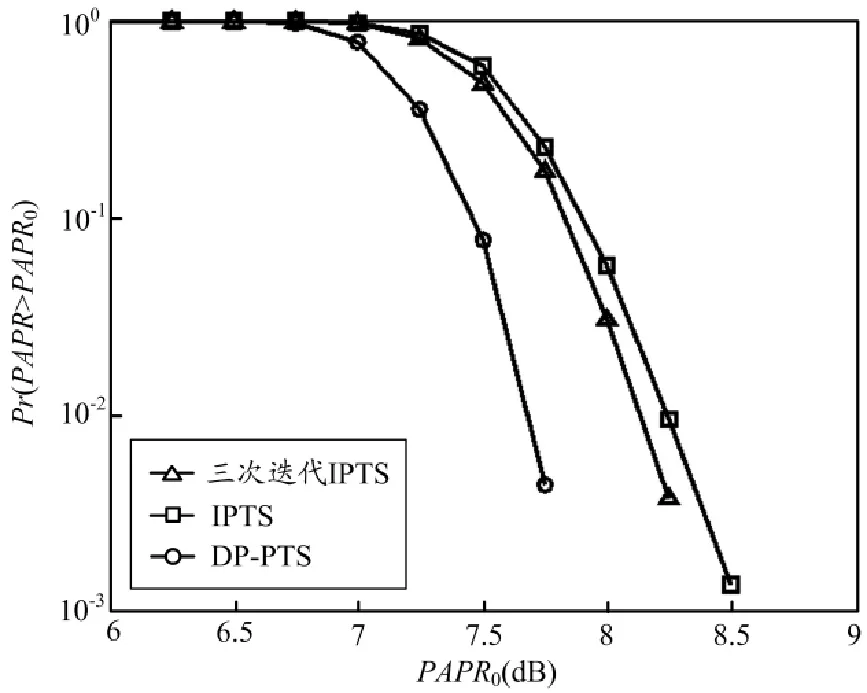
传统PTS方法的搜索复杂度会随着子块数V和相位因子W的增加呈指数增?长，目前有较多能降低PTS计算复杂度的方案[7，8]。Leonard J.Cimini在文献[9]中提出了一种线性迭代PTS方案（IPTS），使用二进制相位因子{1，-1}可以有效降低算法复杂度。IPTS使用迭代思想，先设置所有相位因子bv=1，v=1，2，...，V，计算其PAPR，记为PAPR_min,再依次对相位因子的每一位置-1，计算PAPR。如果PAPR

2　DP-PTS原理

传统的PTS方法只使用一个相位因子，为提高峰均比的性能，我们考虑增加一个相位因子。消息序列通过调制后变为复数序列，有实部和虚部两部分，如果分离实部和虚部，就可以增加一个相位因子。为验证双相位因子的可能性，本文采用迭代的方法进行验证。

在IPTS中，我们采用二进制相位因子{1，-1}。如果把经过IFFT变换后的每一个子块xi，i=1，2，……,V,分为实部和虚部，记为x_reali和x_imagi，i=1，2，……，V，采用两个相位因子b_reali和b_imagi并对其进行迭代，则迭代后的序列yi=b_reali×x_reali+i×b_imagi× x_imagi，b_real∈{1,-1}，b_imag∈{1,-1}。

当b_reali=b_imagi=1时,表示没有相移；当b_reali= b_imagi=-1时，表示对原有子块做180°相移；当b_reali=1,b_imagi=-1时,表示把原有子块沿虚轴进行翻转；当b_reali=-1，b_imagi=1时，表示把原有子块沿实轴进行翻转。对于任意b_real∈{1，-1}，b_imag∈{1,-1}，总存在一个相移φ∈[0,2π)使得yi=ejΦ×xi，φ的值随着x值的变化而变化，由于x不是一个固定值，故φ也不是一个确定的值。但是，不论φ如何取值，对于原序列来说也只是一种相移，通过相位因子我们可以在接收端把原序列恢复出来，因此，双相位因子是可行的。

DP-PTS的主要思想是把经IFFT变换后子块的实部（x_reall）和虚部（x_imagl）进行分离，使用两个相位因子（b_realv和b_imagv）分别对实部和虚部进行相移，通过增加一个相位因子来进一步优化峰均比性能。我们要先通过迭代求出优化后的相位因子bv，v= 1,2,...,V,用bv初始化b_realv和b_imagv，再对b_realv和b_imagv进行迭代优化。

3　仿真结果与分析

3.1仿真与比较

我们仿真对比了PTS、IPTS和DP-PTS方法，仿真参数设置为：基带调制方式为正交幅度调制（16QAM）,子载波数N=1024，过采样因子Nos=4，PTS分块采用相邻分割方式，仿真符号数symbols=3000。使用互补累积分布函数(CCDF)衡量OFDM系统中PAPR的分布：P{PAPR＞z}=1-P{PAPR≤z}，z为门限值。

分块数为4和8时，PTS、IPTS和DP-PTS的性能仿真图如图2所示。其中，PAPR0为峰均比参考值，Pr（PAPR＞PAPR0）为实际峰均比大于峰均比参考值的概率。当分块数为4时，DP-PTS可以获得和PTS相同的性能；当分块数为8时，PTS在峰均比性能上略优于DP-PTS。和IPTS相比，DP-PTS可以获得0.5～0.6dB的峰均比性能优化。

图2　PTS、IPTS和DP-PTS性能仿真

DP-PTS使用迭代的方法，总共需要进行三次迭代，其计算复杂度与三次迭代的IPTS相同。分块数为8和16时，三次迭代IPTS与DP-PTS的性能仿真如图3所示。当分块数为8时，相比一次IPTS，三次迭代IPTS的性能几乎没有提升；当分块数为16时，三次迭代IPTS相比IPTS可以获得0.1～0.2dB的性能提升，在计算复杂度相同的情况下，DP-PTS方法相比三次迭代的IPTS有0.4～0.6dB的峰均比性能提升。

（a）16QAM调制CCDF图，子块数为8

图3　三次迭代IPTS与DP-PTS性能仿真

由于IFFT为线性运算，DP-PTS采用的迭代方法等价于对IFFT变换前的值进行相移，对每一个值，都有4种变换方式，相当于利用迭代在4个相位中选择使峰均比最小的相位值，其计算复杂度与使用4个相位因子{1，-1，j，-j}的IPTS相同。

分块数为8和16时，四相位因子IPTS与DPPTS的性能仿真如图4所示。当分块数为8时，具有四相位IPTS的PAPR性能要优于只有2个相位因子的IPTS；当分块数为16时，由于IPTS采用的是一次迭代的方法，受到一次迭代的局限性，相位因子个数的增加对峰均比性能的影响可以忽略。同样使用迭代的方法，DP-PTS不会受迭代的局限，分块数的增加不会影响DP-PTS的性能。在计算复杂度相同的情况下，DPPTS要明显优于四相位IPTS。

3.2计算复杂度比较

与IPTS相比，DP-PTS通过增加一个相位因子和降低计算复杂度来获得更好的PAPR性能。记分块数为V，相位因子集合包含元素个数为W，本文以PAPR的计算次数来衡量不同方法的计算复杂度，得到几种PTS方法的计算复杂度对比如表1所示。

传统PTS采用全搜索算法，相位因子长度等于分块数，总共有WV种可能，找到使PAPR值最小的相位因子，需要计算WV次PAPR值。IPTS采用二进制相位因子{1，-1}，W=2，每一位翻转后计算PAPR值，需要计算V次PAPR值。DP-PTS在IPTS的基础上再次进行迭代映射，需要计算V+2×V次PAPR值，计算复杂度与三次迭代IPTS和四相位因子IPTS相同，由于采取实部和虚部分离的办法，相位因子变为2×V。由此可知，IPTS和DP-PTS方法的计算复杂度都远小于传统PTS方法。

图4　四相位IPTS与DP-PTS性能仿真

表1　计算复杂度比较

4　结束语

采用PTS优化PAPR是为了寻找计算复杂度和性能之间的一个均衡，IPTS是目前计算复杂度较低的一种PTS算法。为进一步降低计算复杂度，本文提出了DP-PTS。仿真结果表明，DP-PTS在与IPTS获得相同PAPR性能的情况下，具有更低的计算复杂度。本方法可以结合其它降低PTS计算复杂度的方法同时使用。

参考文献：

[1] ZHU Xiaodong, XIA Jinxiang, LI Hong, et al. Ultimate Performance Of Clipping And Filtering Techniques For PAPR Reduction In OFDM Systems [J]. Personal Indoor and Mobile Radio Communications (PIMRC), 2013, 6 (24), 782-785.

[2] ALARAIMI A S, HASHIMOTO T. PAPR And OOBP Of OFDM And Their Improvement By Using Self Cancellation Codings [J]. Wireless Personal Multimedia Communications (WPMC), 2011, 5(8), 1-5.

[3] LEFTAH H A, BOUSSAKTA S. Enhanced Alamouti Space-time Block-coding Transmission Based On A Developed OFDM System [J]. Communication Systems, Networks & Digital Signal Processing (CSNDSP), 2014, 6(9), 591-595.

[4] RAJASEKHAR C, SIRNIVASA RAO D, YASWANTH RAGHAVA V, et al. PAPR Reduction Performance In OFDM Systems Using Channel Coding Techniques [J]. Electronics and Communication Systems (ICECS), 2014, 6(8), 1-5.

[5] BAIG H, JEOTI V. DCT Pre-coded SLM Technique For PAPR Reduction In OFDM Systems [J]. IEEE Intelligent and Advanced Systems (ICIAS), 2010, 5(7), 1-6.

[6] MULLER S H, HBUER J B. OFDM With Reduced Peak-to-average Power Ratio By Optimum Combination Of Partial Transmit Sequences [J]. Electronics Letters, 1997, 5(33),368-369.

[7] MULLER S H, HUBER J B. A Novel Peak Power Reduction Scheme For OFDM [J]. Personal, Indoor and Mobile Radio Communications(PIMRC), 1997, 3(6), 1090-1094.

[8] SHENG JU KU. Low-Complexity PTS-Based Schemes for PAPR Reduction in SFBC MIMO-OFDM Systems [J]. Broadcasting, 2014, 4(60), 650-658.

[9] CIMINI L J, SOLLENBERGER N R. Peak-to-Average Power Ratio Reduction Of An OFDM Signal Using Partial Transmit Sequences [J]. Communications Letters, 2000, 3(4), 86-88.

Dual phase PTS for reducing the computational complexity

FENGZhuo-ming, ZHOULong-long2
( School of Optical and Electronic Information,
Huazhong University of Science and Technology, Wuhan 430074, China)

Abstract:The paper introduces a new partial transmit sequence (PTS) scheme, dual phase PTS(DP-PTS) to reduce the peak to average power ratio (PAPR) of orthogonal frequency division multiplexing (OFDM) systems. It introduces the principle of PTS, IPTS and DP-PTS scheme, carries out the simulation experiment to the three schemes, compares the PAPR performance and the computational complexity of the three schemes.

Key words:OFDM, PAPR, PTS, dual phase PTS, linear iterative PTS

中图分类号：TN911.7

文献标识码：A

文章编号：1002-5561（2016）01-0050-04

DOI：10.13921/j.cnki.issn1002-5561.2016.01.016

收稿日期：2015-10-08。

基金项目：国家自然科学基金(批准号：60902006)资助。

作者简介：冯卓明（1970-），男，博士，主要研究方向为无线宽带通信、OFDM关键技术以及嵌入式系统设计与应用。