基于FCM聚类算法的马田系统研究

任化娟 赵义恒 朱秋平 温彬彬 齐建奎

摘 要：马田系统是一种多元系统定量模式识别方法，是数据分类的有效方法，在很多领域都得到广泛应用。构建正常样本数据的基准空间、筛选出有效的项目、确定阈值等是经典马田系统的重要步骤。文章改进马田系统中筛选有效项目的方法，经典马田系统将正交表和信噪比结合起来筛选有效项目；基于FCM聚类算法的马田系统尝试用FCM聚类算法选择有效项目，正交表的每一行作为一个实验方案，对于每种方案，都利用FCM进行聚类，得到样品分类的正确率。把正确率的信噪比作为筛选有效项目的指标，信噪比越大则选择的有效项目越可信。得到有效的检测项目之后，可以优化马田系统的基准空间，提高样品分类的正确率。

关键词：马田系统；有效项目；FCM聚类算法

筛选有效检测项目是马田系统中的一个重要任务，本文把FCM聚类算法引入马田系统，通过FCM聚类算法更有效地筛选有效项目，优化基准空间。

1 基于FCM聚类算法的马田系统

经典马田系统是一种可以进行诊断、预测、评价，不需要前提假定的数据分析方法，它主要的任务是有效项目的选择有与样本类别识别。基于FCM聚类算法的马田系统优化了经典马田系统有效项目筛选的过程，本文将具体介绍FCM聚类算法、马田系统以及基于FCM聚类算法的马田系统。

1.1 FCM聚类算法

FCM聚类算法是一种基于划分的聚类算法，是数据挖掘的重要方法，它把相似度大的对象划分到同一个簇中，使得不同的簇之间的相似度是最小的。

首先，简单地叙述FCM聚类算法中隶属度函数的概念。隶属度函数是用来表示一个对象隶属于某个集合的程度大小的函数，此函数的值域为“0”到“1”之间的实数，“0”表示这个对象不属于某个集合，相对应地，“1”表示这个对象属于某个集合，介于“0”到“1”之间数表示这个对象既可以属于这个集合也可以不属于这个集合，越接近“1”则属于这个集合的可能性越大。与模糊隶属度函数相适应，隶属矩阵中的元素允许取值为0到1之间的元素，经过归一化，一个数据集的隶属度的和总等于1，隶属矩阵A可表示为：

dij为第i个聚类中心与第j个数据点间的欧几里德距离（即两点之间的真实的距离）；m是一个加权指数，取值范围是1到正无穷。

若要使得目标函数的值最小，则隶属矩阵中元素和聚类中心需要达到最小。

最后，FCM聚类算法确定聚类中心和隶属矩阵的实现步骤是：

Step1：用0到1之间的值随机数初始化隶属矩阵A，使其满足式（1）中的约束条件。

Step2：用式（3）计算第i个聚类中心ci，i=1，…，c。

Step3：计算价值函数。当它小于某个确定的阈值，或它相对上次价值函数值的改变量小于某个阈值，则算法停止。

Step4：用（2）计算新的矩阵。返回step2，进行FCM聚类算法开始迭代，直到目标函数达到最小值。

Step5：按照迭代结果，由最后的隶属矩阵确定数据所属的类，显示最后的聚类结果。

1.2 马田系统

马田系统是一种多元系统定量模式识别方法，它把正交表、信噪比、马氏距离相结合，对待测群体进行分类和检测。

首先，简单地叙述马氏距离、正交表，信噪比和阈值的基本概念。马氏距离是由印度统计学家提出，表示协方差距离，可以有效地计算未知样本之间的相似度，逆矩阵法是最为常用的计算马氏距离的方法。马氏距离表示为：

其中L是正交表的代号，n是试验的次数即正交表的行数，c是有效项目的个数即正交表的列数，正交表中的内容是水平数t，t的取值是“1”或“2”，取值为“1”时表示选择了该有效项目，取值为“2”是表示没有选择该有效项目。

信噪比（SNR）本意是指电子设备或者电子系统中信号与噪声的比例。在马田系统中把信噪比中的信号看为作正常样本，把噪声看作异常样本。若要判断一个不知道偏离程度的异常样本时，SNR越大（即望大特性），则这个样本为异常样本的可能性越大。正交表中第n行望大特性信噪比（SNR）为：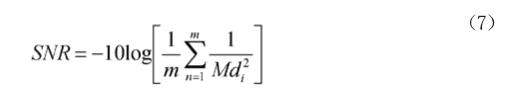

公式（7）中m表示异常样品的个数；Md1，Md2，......Mdm表示异常样本距离基准空间的马氏距离，此时基准空间是由正交表中每一行水平t为“1”的有效项目构成的基准空间。

阈值d0是系统中界限的值，本质上由专业专家确定。马氏距离小于阈值时可判断为正常样本。ROC曲线是反映敏感性和特异性连续变量的综合指标，设置不同阈值，算出一系列敏感性和特异性，然后以敏感性为纵坐标，特异性为横坐标绘制成曲线，曲线下面积越大，诊断准确性越高。由此，可以借助ROC曲线来确定阈值，选择曲线下面积最大点为阈值点。

然后，马田系统的实现步骤为：Step1：构建基准空间，正常总体的样本数据的相关矩阵的逆矩阵是马田系统基准空间。Step2：利用马氏距离公式计算异常样品距离基准空间的马氏距离。Step3：利用公式（6）计算信噪比。Step4：筛选有效项目，构建新的基准空间。Step5：计算待测样品到新构建的基准空间的马氏距离，与阈值比较，小于等于阈值则为正常样品，否则为异常样品。

1.3 基于FCM聚类算法的马田系统

基于FCM聚类算法的马田系统主要改进了马田系统筛选有效项目的方法。在筛选有效检测项目的方法上，经典马田系统通过计算正交表中每一行的异常样本马氏距离的望大特性信噪比，筛选出使异常样本的马氏距离明显异于正常样本马氏距离的有效项目；基于FCM聚类算法的马田系统将FCM聚类算法引入马田系统，利用正交表的每一行来设计实验方案，针对每一种实验方案，都利用FCM算法对随机选取的一组原始样本进行聚类，从而得到每种实验方案分类正确率。按照这样的方式，随机选取多组原始样本，得到多组分类结果的正确率，计算出每种实验方案下的望大特性信噪比，以该正确率的望大特性信噪比作为筛选特征变量的评价指标，进而得到有效的检测项目，对马田系统基准空间进行优化。其他的步骤与经典马田系统类似。把FCM聚类算法融入马田系统后的实现步骤是：Step1：构建马田系统基准空间。Step2：验证基准空间有效性，若无效返回Step1，有效執行Step3。Step3：有效检测项目筛选，按照FCM聚类算法与正交表结合的方法进行筛选。Step4：预测样本的分类，诊断系统的有效性。

2 結语

基于FCM聚类算法的马田系统是将算法对正交表中数据集的分类正确率的望大特性信噪比作为筛选有效项目的评价指标，经典马田系统是将异常样品马氏距离的望大特性信噪比作为筛选有效项目的评价指标。从理论上看，基于FCM聚类算法的马田系统在计算分类正确率的过程中能够更全面地将样本中的数据都参与到有效项目的筛选中，使得有效项目的筛选比经典马田系统的筛选更为有效。

[参考文献]

[1]李昭阳，韩之俊.一种新的判别预测方法——马田系统（MTS）[J].管理工程学报，2000（2）：54-55.

[2]孙晓霞，刘晓霞.模糊C均值聚类算法的实现[J].计算机应用与软件，2008（3）：49-50.

[3]牛俊磊，程龙生.采用优化模型指标筛选的马田系统综合评价方法研究[J].数学的实践与认识，2015（17）：1-12.

Study on MTS Based on FCM Clustering Algorithm

Ren Huajuan， Zhao Yiheng， Zhu Qiuping， Wen Binbin， Qi Jiankui

（Henan Normal University， Xinxiang 453002， China）

Abstract： MTS is a kind of quantitative pattern recognition method for multiple systems，and it is an effective method of data classification. MTS has been widely used in many fields.It is an important step for the classic MTS to construct the reference space of the normal sample data， to screen out the effective items and to determine the threshold value.In this paper， we improve the method of screening effective project in MTS， and the classic MTS combines the orthogonal table and the signal to noise ratio to screening effective project；MTS based on FCM clustering algorithm attempts to use the FCM clustering algorithm to select the effective project.Orthogonal tables each line as an experimental program， for each program， using FCM for clustering to get the correct rate of classification of samples. The correct rate of the signal to noise ratio as the index of screening effective projects；The greater the signal to noise ratio， the more reliable the valid item is selected. After obtaining the effective project， it can optimize the reference space of MTS， and improve the accuracy of the classification of samples.

Key words： MTS； effective project； FCM clustering algorithm