基于滑动窗口模型的数据流加权频繁模式挖掘算法

马连灯 王占刚

摘 要：加权频繁模式挖掘比传统的频繁模式挖掘更加的具有实际意义，针对数据流中的数据只能扫描有限次的性质，提出了基于滑动窗口模型的数据流加权频繁模式挖掘方法WFP-SW，该算法中数据存储采用的是矩阵数据结构，通过矩阵之间的相关操作来产生加权频繁模式。实验结果显示，该算法在产生加权频繁模式的时候不产生冗余模式，比传统的频繁模式挖掘算法有更好的效率。

关键词：数据流；滑动窗口；加权频繁模式；矩阵

中图分类号：TP311.13 文献标识码：A

1 引言（Introduction）

加权频繁模式与传统的频繁模式挖掘是不同的[1-3]，它不仅取决于项集出现的次数，而且要考虑到数据库中项集重要性。在很多实际的应用中[4，5]，不同的数据项的重要程度是不同的。例如，在零售市场分析的时候，虽然贵重的商品没有在事务数据库中出现非常多的次数，但是它们却贡献了很大一部分的收入。所以，加权频繁模式挖掘比传统的频繁模式挖掘更能在现实世界中发挥更实际的作用。

本文提出了基于滑动窗口模型的数据流加权频繁模式挖掘方法WFP-SW，该算法中数据存储采用的是矩阵数据结构，通过矩阵之间的相关操作得到加权频繁模式。实验结果显示，该算法在产生加权频繁模式的时候不产生冗余模式，比传统的加权频繁模式挖掘算法有更好的效率。

2 基本概念（The basic concept）

定义1：设是项的集合，数据流是一个以一定速度连续到达的数据项序列，其中表示第个事务，对于任意都有。每个项目中都有一个代表此项的重要性的非负实数的权值，。

定义2：由数据项组成的集合定义为项集，其中，含有个项的集合定义为项集。

定义3：项集的权值是数据流中含有该项目的事务项集权值的汇总[6]。

定义4：设加权最小支持度为，如果项集是频繁项集，则加权支持度大于或等于，即。

定义5：滑动窗口的起点与终点都没有清晰的限制，的终点就是当前的时间点。的大小是窗口中事务的多少，这个值是提前设置好的。每当有一个新的事务到达时，就滑动一次窗口。新的事务连续进入窗口，同时，旧的事务被删除，滑动窗口一直被更新。

定义6：全序关系。根据字母在字典中的顺序，如果小于，则有，比如[7]。同理，可以给出项集在字典中的顺序为，比如。

在本文中，假设全部项都是依照全序关系排序的。

3 WFP-SW原理与算法（WFP-SW principle and

algorithm）

3.1 矩阵的构造

（1）事务矩阵的构造

用矩阵的行来标识数据流中项的集合，用矩阵的列标识连续到达的事务。设滑动窗口的大小为，如果项集中包含个项，则构造一个的事务矩阵，同时初始化矩阵中的所有元素为0。扫描连续到达的数据流，如果窗口没有满，那么就将连续到达的事务存储进矩阵中，如果项目出现在第条事务中，那么就设置为1，如果没有出现则设置为0；当窗口满的时候，首先把窗口中最旧的事务删除，然后把新到达的事务添加进去。假设事务即将到达，代表最旧事务的列，则最旧事务的删除方法是：。用于记录每列中1的个数，即事务的长度。

（2）二项集矩阵的构造

设项集中有个项，那么构造的加权二项集矩阵是的二项集矩阵，同时初始化矩阵中的所有元素为0。对于加权频繁项集中的两个项和，如果，让中的第行与第行参与逻辑与运算，若支持度不小于，则项集就是加权频繁项集，同时把的值设置成1，反之，把它的值设置为0。

3.2 WFP-SW算法的基本思想

加权频繁项集的产生：项集是通过对加权频繁项集的扩展产生的。设是加权频繁项集，在二项集矩阵中，若，且，则就可以扩充为项集。同时在矩阵中，让对应的个项的行做逻辑与运算，如果得到的结果不小于，则是加权频繁项集。重复这个操作，当没有新的项集产生的时候，结束算法。

3.3 WFP-SW算法描述

综合上面的分析可知，WFP-SW算法有如下关键步骤：初始窗口阶段、滑动窗口阶段、产生加权频繁模式阶段。

该算法的伪代码如下：

输入：数据流事务，滑动窗口大小，每个项目权重，用户设定的最小加权支持度；

输出：加权频繁模式；

滑动窗口中的每个事务

//初始窗口阶段

{

}

//滑动窗口阶段

对矩阵中第列的值进行更新，其他列的值不变

扫描矩阵中的前行，产生

构造二项集矩阵

//产生加权频繁模式阶段，是频繁项集

{

扩展为项集

；

}

4 实验结果及分析（The experimental results and

analysis）

本文中算法采用的实验平台：Windows 7操作系统，Eclipse开发工具，编程语言是java。采用IBM data generator[8]生成的数据作为实验所用的数据。本文采用稠密数据集T40I10D100K，其中D代表事务的总数，I代表最大频繁项集长度的平均，T代表事务长度的平均值，即实验中事务总数是10万条，最大频繁项集的平均长度是10，事务长度的平均值是40。

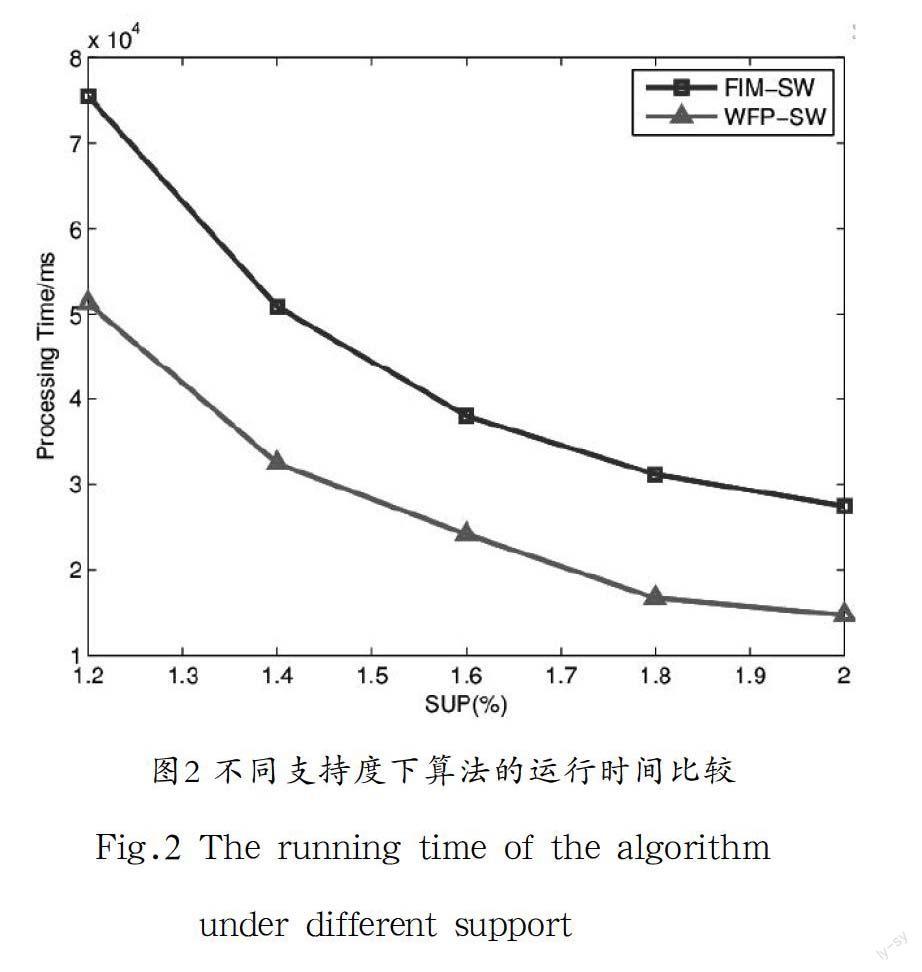
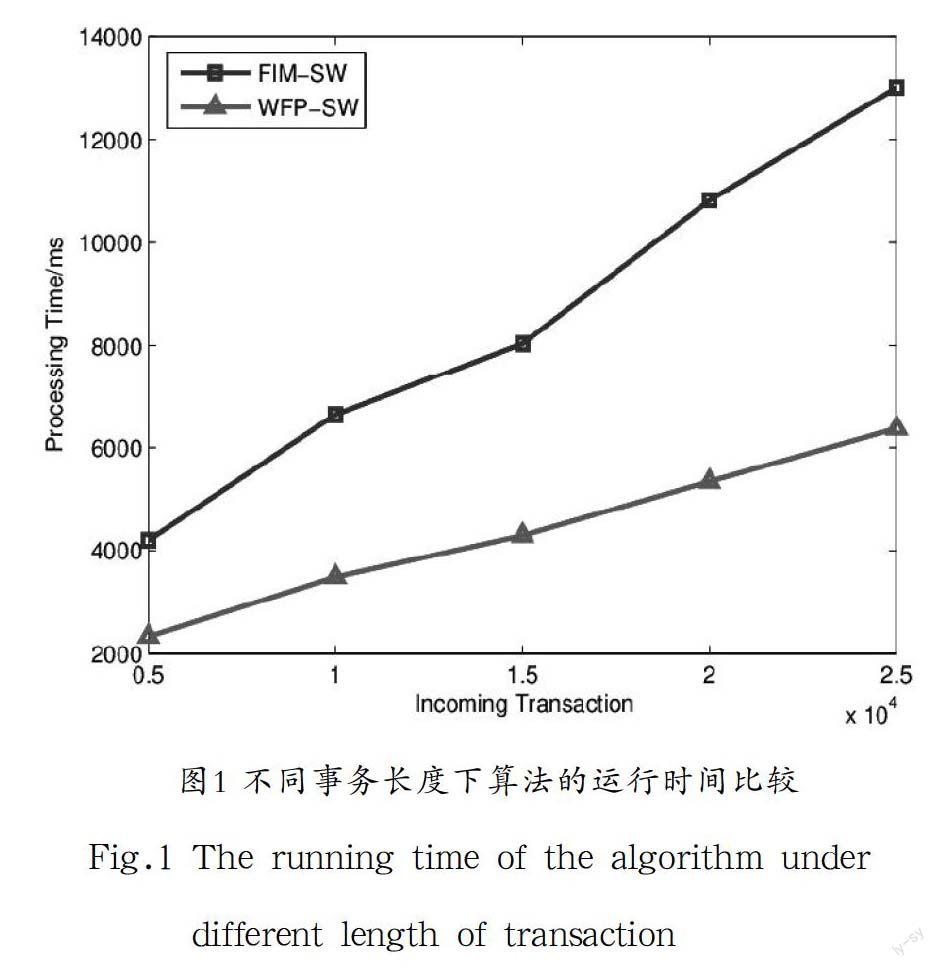
实验对WFP-SW算法和FIM-SW[9]算法进行对比。其中后者是利用Apriori性质产生频繁K-项集，并且在频繁项集产生的过程中，需要进行连接和剪枝操作，所以算法的时间效率比较低。WFP-SW算法在产生加权频繁项集的时候，没有产生大量的候选项集，这样就省去了连接和剪枝的操作，算法的效率显著提高。图1给出了在窗口大小，的前提下，WFP-SW算法和FIM-SW算法随事务数变化的挖掘时间比较；图2给出了在，挖掘五万条事务的前提下，WFP-SW算法和FIM-SW算法随支持度变化的挖掘时间比较。

5 结论（Conclusion）

本文提出了基于滑动窗口模型的数据流加权频繁模式挖掘算法WFP-SW，该算法只需扫描一次数据流，数据存储采用的是矩阵数据结构，通过矩阵之间的相关操作来产生加权频繁模式。同时该算法在产生加权频繁模式的时候不产生冗余模式，通过与算法FIM-SW的对比，验证了WFP-SW算法具有更高的效率。

参考文献（References）

[1] G.Lee，U.Yun，H.Ryang.Mining Weighted Erasable Patterns by Using Underestimated Constraint-based Pruning Technique[J].Intell.Fuzzy Syst.，2015，28（3）：1145-1157.

[2] G.Lee，U.Yun，K.H.Ryu.Sliding Window Based Weighted Maximal Frequent Pattern Mining Over Data Streams，Expert Syst.Appl，2014，41（2）：694-708.

[3] U.Yun，G.Pyun，E.Yoon.Efficient Mining of Robust Closed Weighted Sequential Patterns Without Information Loss[J].International Journal on Artificial Intelligence Tools，2015，24（1）：01-28.

[4] 张晴，高广银.贾波数据挖掘技术在超市营销系统中的应用[J].软件工程，2016，19（5）：35-38.

[5] 孙黎明.探索软件工程数据挖掘技术[J].软件工程，2015，18（5）：

16-17.

[6] FENG Tao，MURTAGH F，FARID M.Weighted Association Rule Mining Using weighted support and significance framework[C].Proc.of the 9th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining，ACM Press，2003：661-666.

[7] 徐嘉莉，陈佳.基于向量的数据流滑动窗口中最大频繁项集挖掘[J].计算机应用研究，2012，29（3）：837-840.

[8] AGRAWAL R，SRIKANT R.Fast Algorithms for Mining Association Rules[C].Proc of the 20th International Conference on Very Large Database.San Francisco：Morgan Kaufmann Publishers，1994：487-499.

[9] 徐建民，郝丽维，王煜.数据流频繁项集的快速挖掘算法[J].计算机工程与应用，2008，44（34）：142-144.

作者简介：

马连灯（1992-），男，硕士，硕士生.研究领域：大数据，数据挖掘.

王占刚（1975-），男，博士，副教授.研究领域：大数据，计算机检测应用，计算机网络安全.