无限长等腰三棱柱均匀载流体在外部空间的磁场分布

赵禹 刘继述 庹晶晶 尹卓 谢蓝霞 付婉琳

摘 要：对磁场分布进行准确计算，可以准确掌握磁场分布规律，不同形状载流体的外部空间磁场分布各不相同，为了能够准确掌握磁场分布规律，需要对不同形状均匀载流体在外部空间中的磁场分布进行计算，在文中主要就无限长等腰三棱柱均匀载流体在外部空间的磁场分布的计算方法进行探讨。利用毕奥—萨伐尔定律计算一定宽度的无限长载流薄板的某点磁场空间分布，再由叠加原理求得整个等腰三棱柱在该点激发的磁场大小，这种方法同样适用于求横截面为任意三角形的无限长载流三棱柱的外部空间磁场分布。

关键词：三棱柱 均匀载流体 磁场叠加原理 磁场大小

中图分类号：TM273 文献标识码：A 文章编号：1674-098X（2016）04（b）-0029-02

对于很多典型的载流体在空间激发的磁场已有不少文献参考，该文利用磁场叠加原理给出在直角坐标系下无限长载流的等腰三棱柱在外部空间的磁场分布方法，以帮助学生加深对毕奥—萨伐尔定律和叠加原理的理解与掌握。

1 磁场计算

1.1 有限宽载流薄板在空间某点的磁场

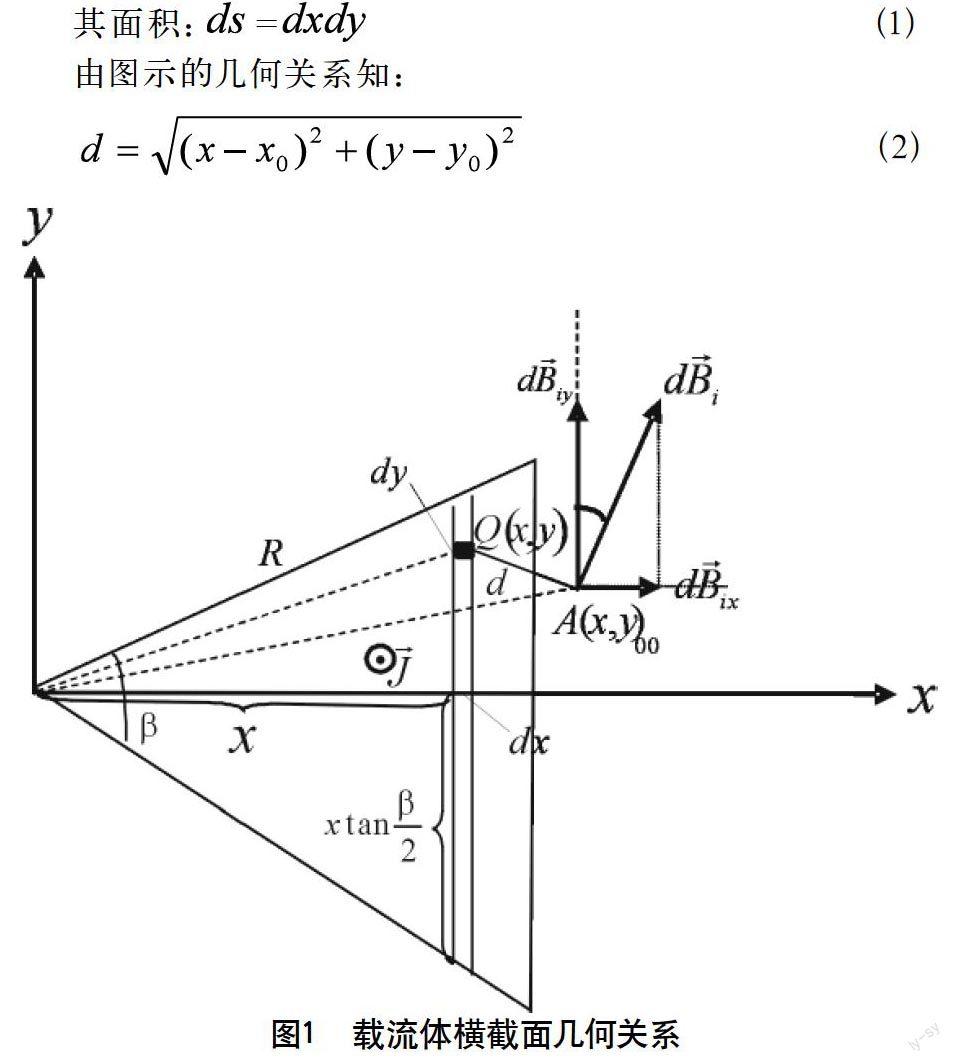
以三棱柱的横切面建立如圖1所示的坐标系：以等腰三角形顶点为原点，以底边的高为轴，以垂直于轴为y轴建立直角坐标系。已知电流方向如图1所示垂直于纸面向上，电流密度为，等腰三角形的顶角为，腰长为。现在考虑场点在三棱外部处。在处取一个宽为的窄条，在窄条上一点处取一长的微元。

将x的上下限代入式（8）、式（9）两式即可分别得到、。由于场点是任意的选取的，所以，对于三棱柱外任意一点的磁场分量表达式不变，只是场点的坐标在变化。

2 结语

对无限长的均匀载流等腰三棱柱在外部空间激发的磁场的求解，本质上就是微元法和叠加原理的应用，计算上的复杂之处在于积分运算。另外对于任意形状的无限长载流三棱柱，我们可以利用同样的方法讨论它在外部空间任意点产生的磁场分布，但是对于柱体内部空间中的磁场分布还有待于进一步讨论。

参考文献

[1] 梁灿彬，秦光戎，梁竹建.电磁学[M].3版.北京：高等教育出版社，2012：177-181.

[2] 同济大学数学系编.高等数学[M].6版.北京：高等教育出版社，2007.

[3] 夏立群.无限长载流导体板的磁场分布[J].内蒙古电大学刊，2006（6）：106.