汇率波动性的近似熵与样本熵分析

刘庆丹 李久华 杨会杰

摘 要：熵估计在生理时间序列上被广泛应用，例如近似熵与样本熵。将熵估计方法应用于汇率时间序列中，用于识别汇率市场在不同时间的波动状态并加以分析。在不同维度下讨论了近似熵与样本熵反映汇率时间序列波动的情况，并对同一维度下近似熵与样本熵效果进行了比较，发现样本熵比近似熵可以更好地反映汇率的波动性，并且更加灵敏。得出样本熵算法在汇率市场中良好地反映了大事件的发生与延续，解决了近似熵算法对微小的复杂性变化不灵敏的缺陷，并且显著提高了熵估计在短时间序列上的可用性和精确度。

关键词：汇率；波动性；近似熵；样本熵

中图分类号：F 822 文献标识码：A 文章编号：1672-7312（2016）04-0438-04

0 引 言

近年来，金融时间序列分析已经越来越受到人们的关注[1-2]。中国汇率市场作为一个发展中市场，其规则、效率、结构等方面还不够规范、有效、成熟。因此，实证研究汇率等金融时间序列的波动情况，对分析金融时间序列的内涵具有重大意义[3]，并对我国经济产生了很多积极影响，例如，对贸易伙伴的合作关系可以进行有效的缓解作用，还可以促进我国加快调整产业结构；当然也有不少人提出了由于人民币兑美元的数值上升而导致的抑制外来资产以及外汇储备大幅缩水等消极影响[4]。

1865年，德国物理学家R.E.Clausius在提出热力学第二定律后的第15年，第一次引入了熵的概念，并且利用熵增加原理来重新定量阐明了热力学第二定律。此后的30多年，熵得到了非常广泛的应用和发展，先后出现了由Boltzmann提出的统计熵，由Shannon提出的信息熵，由Pincus提出的近似熵，由Richman提出的样本熵[5]。从此熵估计就成为了物理学中的一个非常有意义的概念并逐渐渗透到某些社会科学、生命科学、信息论、甚至宇宙学中[6]。

金融时间序列是非平稳、非线性的时间序列，具有序列长度比较短、价格的变化无序不平稳、其他不可控干扰因素较多等特点[7]。近几年来，近似熵（approximate entropy，下文简记为ApEn）与样本熵（sample entropy，下文简记为SampEn）分析方法在解决由于上述序列而出现的问题时发挥了非常重要的作用。近似熵分析方法由 Pincus[8]在k-s熵改进得来的，k-s熵对序列长度有很大的依赖性，而近似熵改进了这一点，即对于有些短的时间序列，也可以得到有效可利用的结论，因而在实证研究金融时间序列特征中有非常多的应用。ApEn（m，r，N）是对相似容限为r，时间序列长度为N的时间序列，在m点数据互相相似情况下m+1点数据互相相似的条件概率CP的负平均自然对数的近似值，因此近似熵是一种标度不变的方法。

从近似熵的算法可以看出，近似熵的定义中存在着对自身数据段的匹配，以至于它无法对对很小的复杂性变化进行有效的解读。因此，需要改进此种方法来克服这种偏差产生的影响，即要消除自身匹配。

样本熵分析方法是由Richman等在基于近似熵的基础上改进来的，近几年得到了越来越多的接受、关注与认识，被广泛应用于生物、临床、金融、医学等领域[9]。相对于近似熵而言，样本熵不包括自身数据段的匹配，计算方法也不需要很长的数据长度，具有更好的相似性、一致性，由于数据丢失而产生的问题也不敏感。

1 近似熵与样本熵

近似熵是近些年来才发展起来的一种可以度量时间序列复杂性和统计量化的规则。它是在20世纪90年代初由Pincus为了克服在混沌系统中求解熵特别麻烦才提出的。

近似熵是对非线性时间序列复杂性的一种非负的定量描述，它对于相对较短的（大于100个数据点）、含噪声的时间序列进行计算分析，使其显示出潜在的应用价值，这是由于产生近似熵的主要的技术思想是：它并不是试图完全重新构造吸引子，而是用一种简单且有效的统计方式——边缘概率分布的不同来区分各种不同的运动过程，其中吸引子是一个数学上的概念，用来描写运动的收敛类型；边缘概率在数学概念中是指当实验所获取的事例按不同的标准进行分类时，忽略掉某些分类标准而只考虑在某一种分类标准下某事件出现的概率。

参数m和r的选择非常重要，如果m过大或者r过小，小于阈值r的匹配数会过少；同时，如果m过小r过大，所有的模版都匹配。Pincus建议当数据长度N为100到5 000时，m一般取1或者2，r取0.1到0.25倍的序列标准差。但是这个建议对不同的数据集并不总是能得到最优的结果。下面结合matlab程序来说明近似熵的算法步骤。

样本熵是由Richman提出的一种新的时间序列复杂性测度方法[10-11]。它是由近似熵改进而来的，用意于消除近似熵由于自身匹配而造成的计算偏差，弥补其对微小的复杂性变化不灵敏的缺陷，是一种比近似熵精度更好的方法。样本熵的计算步骤如下

SampEn（m，r，N）=-lnBm+1（r）/Bm（r）」.

样本熵的物理意义与热力学熵相同，主要用来定量刻画系统的复杂度或无序性。样本熵值越低，序列自我相似性越高，产生新模式的概率越低，时间序列越简单； 反之，样本熵值越高，序列自我相似性越低，产生新模式的概率越高，时间序列越复杂。

2 实证分析

文章搜集了从1994年1月10日至2014年12月31日人民币兑美元的汇率，共5 477个数据，由于每一年都会有一个近似熵值和样本熵值，所以将每一年的数据修正成为同等长度的时间序列，即将在同等时间位置上存在缺失数据就将此时间点全部删除，于是就得到了从1994年到2014年每年都有256个数据点；为了消除不同数据之间的量差，在数据分析过程中，所采用的数据为1994年1月10日至2014年12月8日共21年的人民币兑美元的汇率一阶差分数据，如图1所示。通过近似熵与样本熵方法，来分析中国汇率市场不同时间上的复杂性特点，并进行比较。

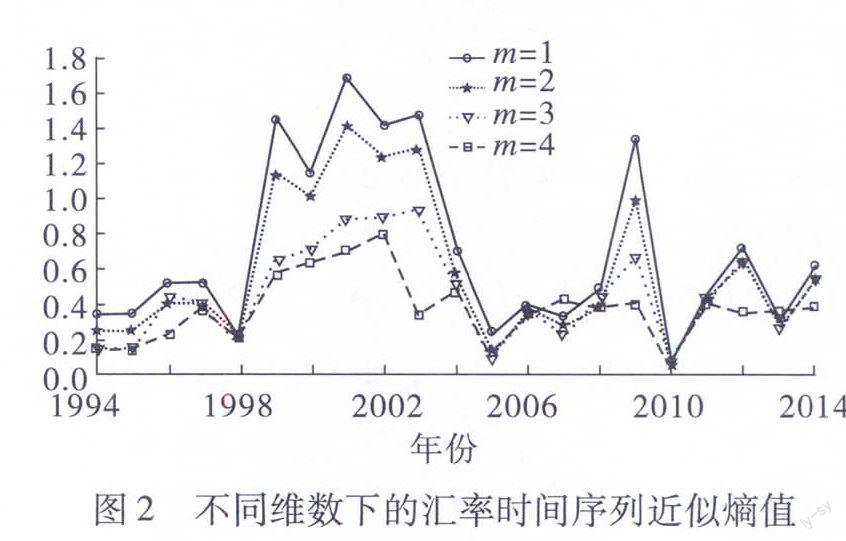
图1 汇率一阶差分数据利用matlab得出从1994年到2014年的近似熵，并画出了m=1到m=4不同维度下汇率时间序列近似熵的变化趋势，结果如图2所示。我们从中可以看出近似熵值在1998年、2004年、2005年、2010年发生了骤降。但是2000年的美国新经济危机，2001年的“9·11”恐怖袭击事件，2008年的环球金融危机从图2的近似熵值并不能显现出来，所以在很大程度上近似熵并不能很好地说明汇率的波动性；并且不同维数下近似熵值变化明显，说明近似熵值与数据的个数有很大的关联，数据量越大近似熵值越小，所以在数据量小于一定程度时，近似熵不能反映汇率时间序列真实的波动趋势。

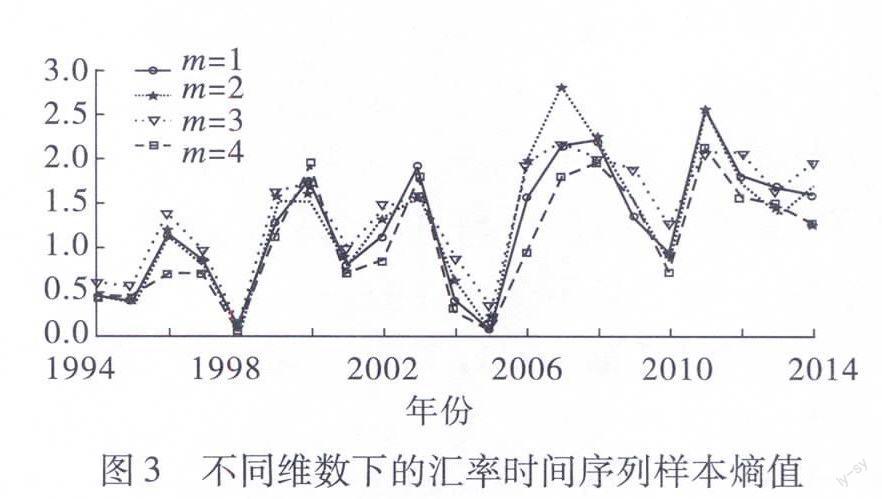
利用matlab得出从1994年到2014年的样本熵，并画出了m=1到m=4不同维度下汇率时间序列样本熵的变化趋势，结果如图3所示。通过图3，我们可以清楚地看出样本熵值在1998年、2001年、2004年、2009年、2010年都发生了骤降。1996年我国实现人民币经常项目可兑换，外汇政策进行了重大调整，1997年的东南亚金融危机，2000年的美国新经济危机，2001年的“9·11”恐怖袭击事件，2008年的环球金融危机。亚洲金融危机是由于泰国实行浮动汇率制而导致的，并迅速在整个亚洲蔓延，直至1998年年末才逐渐平息，对亚洲许多国家的金融市场造成了很严重的打击，中国也因此而被连累，导致了汇率的不平稳。2008年的环球金融危机是由于美国的次贷危机的发生，雷曼兄弟的破产也是导火索，继而引发了严重的货币流动性危机，最终影响了全球经济的动荡。从亚洲金融危机的经验教训看，许多国家货币大幅贬值，非但没起到刺激当地出口的作用，相反，不仅打击了本国金融业，也造成通货膨胀，资产缩水，资金外流，最后酿成全面经济危机[12]。而当时我国经济之所以“一枝独秀”，与人民币的稳定是分不开的。最近，东南亚一些国家的货币再次贬值，结果出口下滑更快。如果此时人民币贬值，则不可避免地会出现竞相贬值的局面，酿成新的危机。

由此可以看出样本熵在此时可以很好的反映汇率时间序列的波动情况；并且汇率时间序列的样本熵值在不同维度下并没有发生太大的变化，说明此时的数据量已经做够样本熵算法进行精确的计算了。

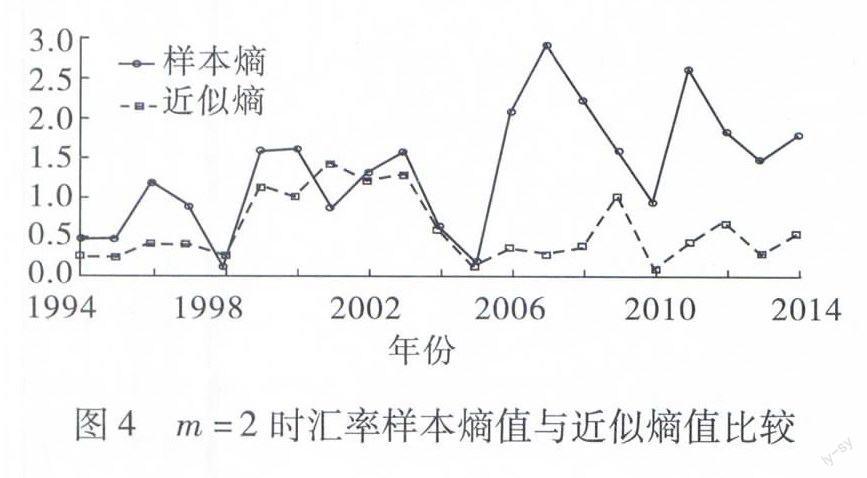
为了更明显的看出样本熵值与近似熵值的不同，文章将m=2时的样本熵值与近似熵值进行对比分析，如图4所示。我们可以明显的看出在2001年时，样本熵值发生了骤降，而近似熵值却仍然在上升，即此时的近似熵算法没有反映出2000年的美国新经济危机、2001年的“9·11”恐怖袭击事件和2008年的环球金融危机对中国汇率市场的影响；在2008年和2009年时，近似熵值虽然也上升了，但上升幅度很小，说明近似熵的灵敏程度不如样本熵。并且近似熵数值相对于样本熵数值较小，熵值越小代表时间序列越简单，而事实上汇率市场数据变化幅度很大，所以样本熵比近似熵能更好的反映汇率时间序列的波动情况。

3 结 语

文章将熵估计方法应用于汇率时间序列中，用于识别汇率市场在不同时间的波动状态并加以分析。在不同维度下讨论了近似熵与样本熵反映汇率时间序列波动的情况，并对同一维度下近似熵与样本熵效果进行了比较，发现样本熵比近似熵可以更好的反映汇率的波动性，并且更加灵敏。样本熵算法在汇率市场中良好的反映了大事件的发生与延续，解决了近似熵算法对微小的复杂性变化不灵敏的缺陷，并且显著提高了熵估计在短时间序列上的可用性和精确度，并且样本熵算法可以应用于医学、金融和多种时间序列数据中，它也可以应用到更短的股票数据中。例如一周或一天不同节点的单只股票中，检测它是否稳定，如果熵值较高，序列变化无序，不宜进行投资；如果熵值较低，序列平稳有序，可以结合统计上的预测方法，进行投资规划。该算法的提出为短时间序列的检测提供了新的思路。

参考文献：

[1] Ghashghaie S，Breymann W，PeinkeJ，et al.Turbulent cascades inforeign exchangemarkets[J].Nature，1996，381（6 585）：767-770.

[2] Laloux L，Cizeau P，Bouchaud J P，et al.Noise dressing of financial correlation matrices[J].Physical Review Letters，1999，83（7）：1 467-1 470.

[3] 赵丽丽，唐 镇，杨会杰，等.基于复杂网络理论的时间序列分析[J].上海理工大学学报，2011（1）：47-52.

[4] 戴莹星，孙宗国.人民币汇率的变化及其对中国经济的影响[J].法制与社会，2008（7）：100-101.

[5] 严捷冰，杨会杰.基于扩散熵的平衡估计的儿童行走序列研究[J].上海理工大学学报，2014（2）：147-153.

[6] 苑 娟，万 焱，褚意新.熵理论及其应用[J].中国西部科技，2011（5）：42-44.

[7] 乔坎坤，卢志明.扩散熵方法对股指内在规律性的分析[J].复旦学报：自然科学版，2013（5）：712-716.

[8] Pincus S，Kalman R E.Irregularity，volatility，risk，and financial market time series[J].Proceedings of the National Academy of Sciences of the United States of America，2004，101（38）：13 709.

[9] Costa M，Goldberger A L，Peng C K.Multi-scale entropy analysis of complex physiologic time series[J].Physical Review Letters，2002，89（6）：068 102-1-4.

[10]Richman J S，Moorman J R.Physiological time-series analysis usingapproximate entropy and sample entropy[J].American Journal of Physiology-Heart and Circulatory Physiology，2000，278（6）：2 039-2 049.

[11]Lake D E，Richman J S，Griffin M P，et al.Sample entropy analysis of neonatal heart rate variability[J].American Journal of Physiology-Heart and Circulatory Physiology，2002，283（3）：789-797.

[12]张灏泉.分析人民币汇率对我国经济的影响[J].现代管理科学，2003（1）：76-77.