基于小波对传统语音抗噪的提升方法
杨荔琴

摘 要:处理语音信号得到所需的音频参数就能高速地传递、储存语音信号,或者运算后实现某种用途的目的,而该过程基础是参数提取,利用小波提升的方法可提取语音信号的一些参数,并对语音信号进行处理。利用小波提升变换对语音数据进行压缩编码,这种方法不仅可以达到较高的压缩比,而且重建后的语音失真很小。
关键词:语音信号;小波提升;语音去噪
1 前言
在数学领域中小波分析作为一颗新星在当今高速发展,不仅具有成熟的理论而且被应用到了各个领域。在时域就可进行小波的提升变换,不必要变换到频域,而且基本常见的小波均可以通过这种方法构造出来。信号的小波变换相当于其通过一组滤波器。经过小波变换后,信号的能量会被汇集在个别系数上,所以系数的取值肯定比其能量分布在大多数小波系数值大。
2 离散序列小波变换(DTWT)
首先对带有噪声的声频信号做离散序列小波变换(DTWT),获得具有噪声的小波系数;其次取合适的门限值,利用明显大于阈值的小波系数经过变换恢复语音信号,用软限幅函数对门限值做适当变换,软限幅函数为
式中表示被门限处理后的小波系数,t表示软限幅函数的门限值,门限值t的取值对去噪的结果影响较大。抬高门限值t能够降低重构信号中的噪声,但会使重构信号有一定的失真;减小阈值,也会减小重构信号畸变,但会使增强重构信号中的噪声。阈值t的确定一般采取文献讲解的决策门限进行估计。即
其中σ是噪声的方差,σ用median(abs(cd1))/0.6745,cd1 为小波分解的第一层高频系数;N 是带有噪声的语音序列的长度.此处的判决门限t是不变的,显然不能用t对不同尺度的信号做抑制噪声小波系数。为此,需要采用随尺度变化的判决门限,此处规定新的阈值为,若尺度j增长,门限值会随之降低,和噪声的小波变换的特性相同。
3 用一维小波变换对降低语音信号噪声的MATLAB仿真
去除噪声提升小波变换分为如下三步:第一,对信号做提升小波变换,每变换一次将信号解析为新的近似尺度系数c(n)和小波系数d(n);第二,对小波变换后的系数做门限值紧缩处理;第三,合成紧缩处理后的小波系数和尺度系数,产生去噪后的信号。
在MATLAB中利用一维小波分析来降低信号噪声,常使用函数wden和wdencmp实现。用wden函数时,得到的是对原信号降噪后的信号。wdencmp 函数能够对一维或二维信号直接做降噪或压缩处理,方式与上述类似。
4 相同门限值下小波函数及其对应的提升函数的降躁处理效果
下面在同一阈值(0.0546,由ddencmp 函數自动获得)下,分别用sym6、haar、db4小波及其对应的提升小波进行降噪处理,使用sym6小波的MATLAB程序和其小波提升程序,试验时加入噪声,在同一信噪比下进行实验。这里的噪声是由randn 函数产生的高斯白噪声,其幅度设定为0.01。
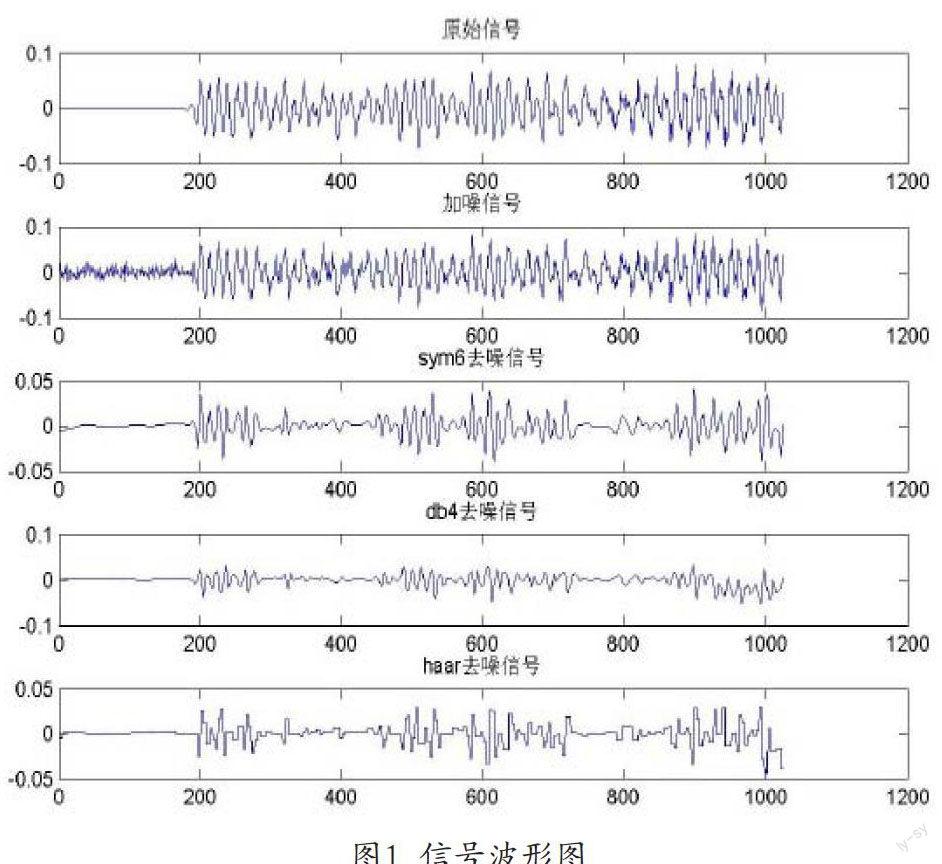
仿真图形:
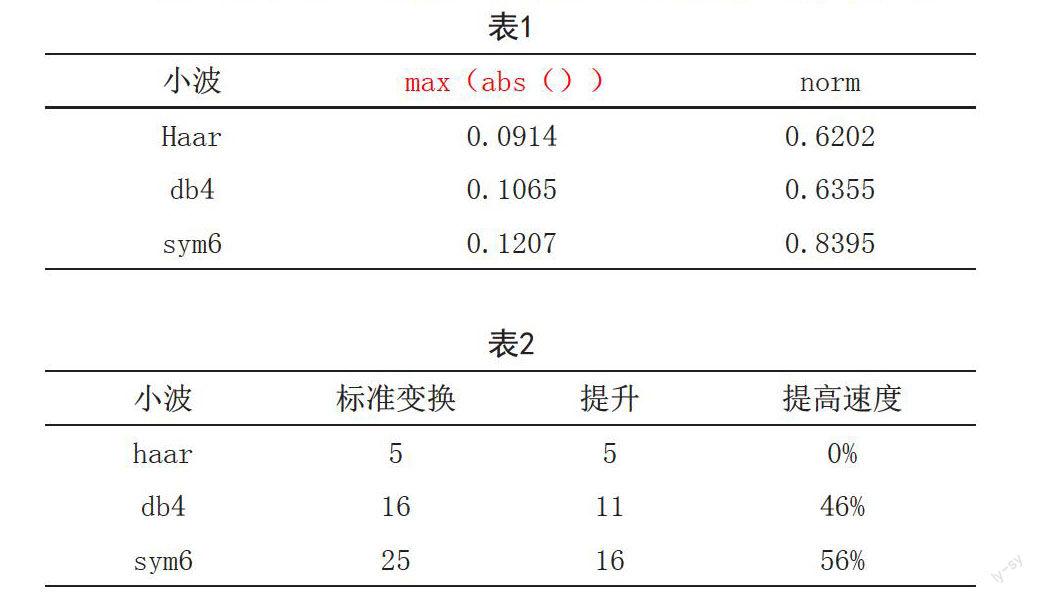
由图1可得,降噪后去掉了所掺杂的噪声,保存了原信号中的聚变部分,和原信号十分相似,其中使用sym6小波的信号与原信号更为相似,小波去噪的效果十分明显.从表1中得到sym6小波最大差绝对值max(abs())最小,原信号与重构信号矩阵差范数norm也最小,即与原来的图像最为靠近。
三种小波降噪处理时相应的最大差绝对值和矩阵差范数
表2结果表现出对语音用不同的小波进行处理时,分别采用标准变换和提升方法实现语音处理所需的时间比较,使用提升方法的速度更快。
由于用sym6 小波处理的信号与原始信号更为接近,去噪的效果最好,所以选用sym6小波进行提升处理,在同一信噪比和阈值(thr=0.0546)下比较两者的去噪效果。见效果图和表3
原始语音信号‘01.wav
通过表3可以看到,用sym6小波和其提升小波进行去噪时,当用相同的信噪比和近似均方差时,提升小波去噪在时间上也远小于传统方式。
经过比较发现采用提升方式实现的语音消噪相对采用传统方式实现的语音消噪,量上没有任何影响,但是实现速度明显加快,计算及编程也较为快捷容易。是以,用小波提升去噪方式具有较好的实用性。
参考文献
[1]涂丹,甘亚莉,李国辉.基于格形结构的正交小波滤波器优化设计方法[J].计算机工程与科学,2004,(12):42-45.
[2]刘娟花,李福德.一种改进的小波域语音去噪方法研究[J].西安工程科技学院学报,2006,(1):92-95.

