将平面扇形板材拓扑成类黑洞结构的方法方程

王东辉

摘 要：文章介绍了一种新发现的‘非对称曲折效应以及它的计算方法和对应方向。‘非对称曲折效应主要是曲环夹角度与曲率的互换现象。利用这个原理可以将平面扇形金属材料拓扑成‘立体反向复合梯形曲环。而这种曲环的形状又跟黑洞类似。因此或可以根据黑洞的半径和夹角度以及夹角两边的宽度，计算出其拓扑在平面的形状和尺寸。也或可以根据这个原理，通过对能量_动量运动路径中与场形成的夹角的测量，并根据所得夹角度对应的‘场压力值来计量其所对应的能量_动量的大小及空间加速度快慢。曲率和夹角度可以互换的发现，使人类对空间和自然的本质有了新的认识。

关键词：非对称曲折效应；夹角度与曲率的互换；扭量；黑洞

0 引言

笔者从事古陶瓷收藏，有许多破损瓷器需要用古代镶口工艺修复。然而请教了很多人竟都不知道确切的下料方法。且多数认为古人的精湛工艺仅仅是工匠的‘手艺不错。但我相信这里面一定有科学的作用。经过3年左右的思考和一百多次的实验，发现剖面为夹角的立体金属曲环可以通过计算在平面金属板上画出图，然后剪下并采用‘曲折得到。而要顺利完成这个过程的关键点在于：1.要知道曲折线两边宽度的不对称比值。如果比值不正确，曲环在曲折时就会出现褶皱和变形。2.要知道曲环在曲折过程中夹角度与曲率，半径的变动关系。也就是说在曲环曲折时，随着夹角度的变化，它的曲率和半径是怎样跟着变化的。而这些数据都需要通过实验采集，然后再根据规律推导出通用的计算方法。当笔者把平整的立体曲环做出来后，又迷惑于其成型原理及形状在现实中的对应。当看到黑洞的图片后才似有所悟，并思考两者间存在关联的可能。而后又发现能量_动量在运动中与场挤压产生的波纹都具有夹角状，让我进一步思考这种现象与‘非对称曲折效应的关联。

1 首先说明一下摘要中的“非对称曲折效应”，“拓扑”和“类黑洞结构”的含义。

1.1 什么是“非对称曲折效应”？

本实验中的‘非对称曲折效应是指将厚度，密度相同的平面扇形金属板材（下简称‘平面扇环）沿着刻划好的曲分界线作曲线对折，使之变成立体‘反向复合梯形曲环（下简称‘立体曲环）。而曲分界线两边材质的宽度是1：3比例。在曲折过程中，曲环的曲率和半径随着夹角的变化而变化。整个‘曲折过程，实际就是曲环夹角度与曲率，半径的交换过程。鉴于‘非对称曲折现象的特殊性，笔者把这种交换过程定义为‘非对称曲折效应。将曲折的材料视为扭量体，曲折线两边的曲面材料之间视为扭量关系，曲折线两边曲面材料对应圆心的宽度值视为扭量值。

1.2 为何说这是一种拓扑关系？

因为从平面扇环曲折成立体曲环是曲率，半径与夹角度的交换过程。除了曲率的变化和曲折线部位因夹角度的变小引起材料外部不可避免的延展。理论上在‘曲折后的立体曲环内部空间仍与‘曲折前的平面扇环面积相等。从这个角度衡量，这是平面扇环和立体曲环的拓扑关系。

1.3 如何得出与黑洞有关联？

通过实验得到的‘立体曲环和黑洞图片进行比较，直观上非常相似。关联度有多大？，笔者认为可通过测量黑洞夹角两侧的宽度比例对比本实验中的立体曲环两侧的‘扭量值比例是否相同得出结论。

2 图文解说

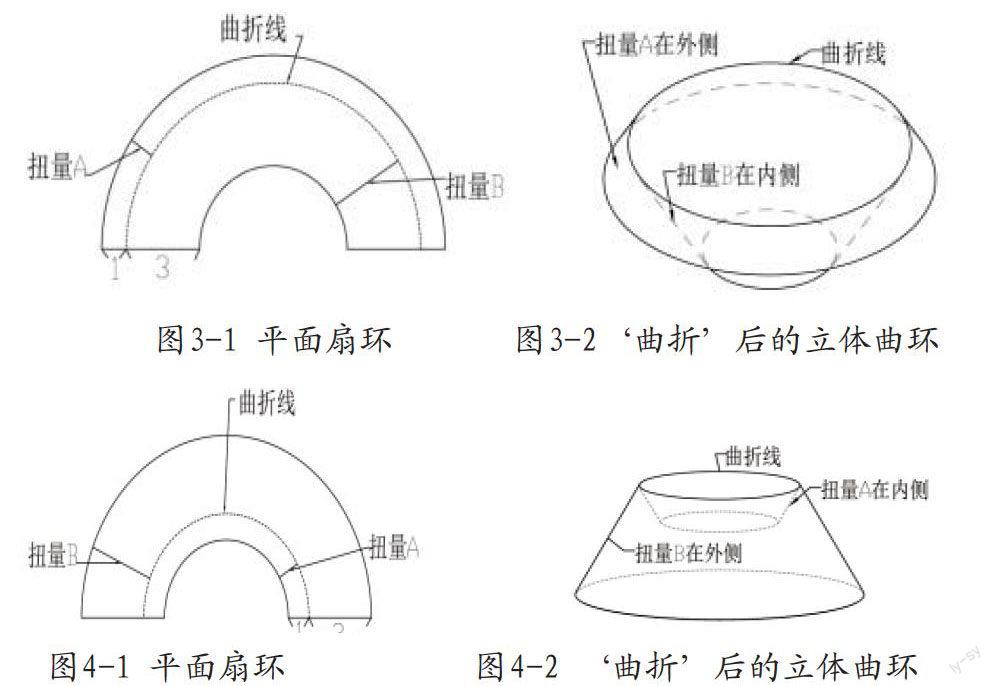
解释一下上面2组图标示的含义

（1）曲折线：曲折线是扭量A、B的曲分界线，也是曲环夹角的顶部。它无限小，在曲折时受力是扭量A、B之和。

（2）扭量A：扭量A在‘立体曲环剖面较窄的一边。它的扭量值是扭量B的1/3。

（3）扭量B：扭量B在‘立体曲环剖面较宽的一边。它的扭量值是扭量A的3倍。

（4）图1和图2的区别在于：两者的扭量位置相反。但扭量之间的不对称比例相同。

3 什么是‘不可折临界夹角度及具体值？

首先要明确这种复合曲环是两个‘梯形曲环的反向连体结构。为了了解其基本特性，笔者将平面扇环进行卷曲实验。图中可以看出，不管卷的曲率有多大，卷曲环仍有斜度。因此两个有斜度，且反向连体的梯形曲环，必定会留有夹角形空隙。实验表明，当曲环被曲折到30度夹角时便不能再曲折，否则曲环就要变形。因此30度夹角是立体曲环的‘不可折临界夹角度。

4 实验方法

选一块厚薄适中，结构匀称，有一定塑性和延展性的平面金属板材。放平和固定后，标示出圆心和各条曲线的半径值位置。再用滚轮圆规压出曲折线和各扭量值的边界线。注意；扭量A和扭量B的扭量比值一定要1：3，且每条曲线的曲率必须相同。然后沿扭量值边界线剪下。再用平钳夹住扭量A一边，另一手握住扭量B一边。沿着曲折线小幅度的来回曲折。待接近目标半径和曲率后，把曲环套在所求尺寸，剖面为夹角的金属曲环上拓平即可。

5 如何计算立体曲环拓扑在平面的尺寸

要计算立体曲环拓扑在平面的尺寸，关键需要了解夹角度与曲率，半径的变动比值。即在曲环夹角度变大过程中，曲折线的曲率和半径相应的缩小和增长了多少？

从实验数据中发现：曲折前后的曲环曲折线曲率和半径的乘积相同。由此得出这样一个定律，即：曲线一样长的曲环，它们的曲率和半径的乘积一定相等。那么想要知道曲环夹角变动后的曲折线曲率或半径，就可以通过曲环夹角变动前的曲折线曲率和半径的乘积除以夹角变动后的曲折线曲率或半径的其中一个值，得出另一个值。

但这个定律，只能说明曲环在夹角度变动下，所变化出的不同曲率和半径的乘积都相同。并不能得出曲环在特定夹角度下，它的平面曲折线的曲率和半径值分别是多少。但这个定律的发现，拓展了笔者的思路。使笔者尝试通过立体曲环夹角度和平面曲折线曲率或半径的乘积规律去找出夹角度对应的平面曲折线半径或曲率。

通过对实验数据的检查发现：同半径，60～30夹角度区间的立体曲环，它们曲折前的平面扇环曲折线半径与曲折后的立体曲环夹角度的乘积（下简称：‘平夹乘积）都相同。因此求立体曲环在60～30夹角度区间之对应的平面扇环曲折线半径=区间内任意曲环夹角度与其曲折前平面扇环曲折线半径的乘积÷所求曲环夹角度。

后又通过一系列推导和实验（过程省略）得出：立体曲环在180～60夹角度区间的“平夹乘积”需要从180夹角度与所求立体曲环的半径相乘的乘积（下简称：‘立夹乘积）基础上递减求得。

其递减规律是：曲环夹角在180～150夹角度区间时，每小1夹角度即递减‘立夹乘积的0.004444..倍值作为它的‘平夹乘积。

设平面扇环曲折线半径为Qar，所求立体曲环曲折线半径为x.Qbr，其中x代表未知数，Qbr代表立体曲环半径。夹角度为L°，所求立体曲环夹角度为Ψ。

说明：把所求曲环曲折线半径值和所求曲环夹角度代入方程，就能得出该曲环的平面扇环曲折线半径值（下简称‘平面曲折线半径）。

那么求曲环夹角在180-150度区间所对应的平面曲折线半径Qar={180L°×x.Qbr-180L°×x.Qbr×0.004444..倍×（180L°-Ψ）}÷Ψ

而曲环夹角在150-120度区间时，它们的‘平夹乘积是从‘立夹乘积的86.66..%值的基础上递减。然后从150度开始算，每小1夹角度再减去‘立夹乘积的0.003333..倍值。

即：求曲环夹角在150-120度区间所对应的平面曲折线半径Qar={180L°×x.Qbr×0.8666..-180L°×x.Qbr×0.003333..倍×（150L°-Ψ）}÷Ψ

曲环夹角在120-90度区间时，它们的‘平夹乘积是从‘立夹乘积的76.66..%值的基础上递减。然后从120度开始算，每小1夹角度再减去‘立夹乘积的0.002222..倍值。

即：求曲环夹角在120-90度区间所对应的平面曲折线半径Qar={180L°×x.Qbr×0.7666..-180L°×x.Qbr×0.002222..倍×（120L°-Ψ）}÷Ψ

曲环夹角在90-60度区间时，它们的‘平夹乘积是从‘立夹乘积的70%值的基础上递减。然后从90度开始算，每小1夹角度再减去‘立夹乘积的0.001111..倍值。

即：求曲环夹角在90-60度区间所对应的平面曲折线半径Qar={180L°×x.Qbr×0.7-180L°×x.Qbr×0.001111..倍×（90L°-Ψ）}÷Ψ

曲环夹角在60-30度区间时，它们所有的‘平夹乘积都为‘立夹乘积的2/3值。为了方便计算，这个值也可以理解成‘立夹乘积的0.6666..倍值。

即：求曲环夹角在60-30度区间所对应的平面曲折线半径Qar=（180L°×x.Qbr×0.6666..倍）÷Ψ

在求得平面扇环曲折线半径值后，再根据‘曲长相等，半径和曲率的乘积也相等定律求出平面扇环曲折线曲率。

即：平面扇环曲折线曲率=立体曲环曲折线曲率×立体曲环曲折线半径÷平面扇环曲折线半径。

设平面扇环曲折线曲率为Qa?S，半径为Qar。立体曲环曲折线曲率为Qb?S，半径为Qbr。

简化为Qa?S=Qb?S×Qbr÷Qar

在计算完平面扇环曲折线半径和曲率后，还要算各扭量值边界线的半径值。（注；由于各扭量值边界线的曲率与曲折线一致，不用再求）。边界线半径值可以按具体扭量值从‘平面曲折线半径基础上加减求得。外扭量值采用加法，内扭量值采用减法。

即：求扭量A在外侧时的平面边界线半径=平面曲折线半径+扭量A值。

求扭量值A在内侧时的平面边界线半径=平面曲折线半径-扭量A值

求扭量B在外侧时的平面边界线半径=平面曲折线半径+扭量B值

求扭量B在内侧时的平面边界线半径=平面曲折线半径-扭量B值

6 如何求夹角在动态下的曲环曲率和半径的变化值

如果我们要计算夹角在动态下的曲环曲折线曲率和半径的变化值。或者用于立体曲环与平面扇环互相拓扑时的换算，则可以用一个更简便的计算方法。即预先算出立体曲环夹角度对应的平面曲折线半径是立体曲环半径多少倍的值（下简称：平立倍率值），即用‘平夹乘积求得的平面曲折线半径值÷立体曲折线半径值得出。而求得的‘平立倍率值也是立体曲环曲折线曲率是其夹角度对应的平面曲折线曲率多少倍的值。再用‘平立倍率值与夹角变动前的曲环曲折线曲率和半径值进行计算，得出夹角变动后的曲环曲折线曲率和半径值。

设未知‘平立倍率值为x.a.a..，其中x代表未知数，a.a..表示倍率值。另说明一下：经运算发现在原方程中代入任何自然数作为半径值，求得的倍率都一样。因此下列方程中的n.Qbr表示任何半径值，其中n表示任何自然数。

即：曲环夹角在180～150度区间所对应的‘平立倍率值x.a.a..={180L°×n.Qbr-180L°×n.Qbr×0.004444..倍×（180L°-Ψ）}÷Ψ÷n.Qbr

曲环夹角在150～120度区间所对应的‘平立倍率值x.a.a..={180L°×n.Qbr×0.8666..-180L°×n.Qbr×0.003333..倍×（150L°-Ψ）}÷Ψ÷n.Qbr

曲环夹角在120～90度区间所对应的‘平立倍率值x.a.a..={180L°×n.Qbr×0.7666..-180L°×n.Qbr×0.002222..倍×（120L°-Ψ）}÷Ψ÷n.Qbr

曲环夹角在90～60度区间所对应的‘平立倍率值x.a.a..={180L°×n.Qbr×0.7-180L°×n.Qbr×0.001111..倍×（90L°-Ψ）}÷Ψ÷n.Qbr

曲环夹角 在 60-30 度 区 间 所 对 应 的 ‘ 平 立 倍 率 值x.a.a..=（180L°×n.Qbr×0.6666..倍）÷Ψ÷n.Qbr

那么求夹角度变大后的曲折线半径=夹角度变大前曲折线半径×（夹角度变大前对应的“平立倍率值”÷夹角度变大后对应的“平立倍率值”）

求夹角度变大后的曲率=夹角度变大前曲折线曲率÷（夹角度变大前对应的“平立倍率值”÷夹角度变大后对应的“平立倍率值”）

求夹角度变小后的曲折线半径=夹角度变小前曲折线半径×（夹角度变小前对应的“平立倍率值”÷夹角度变小后对应的“平立倍率值”）

求夹角度变小后的曲折线曲率=夹角度变小前曲折线曲率÷（夹角度变小前对应的“平立倍率值”÷夹角度变小后对应的“平立倍率值”）

“平立倍率值”也能用于立体曲环和平面扇环的相互拓扑计算：

即：求平面扇环曲折线半径=立体曲环曲折线半径×夹角度对应的‘平立倍率值。

简化为：Qar=Qbr×x.a.a..

求平面扇环曲折线曲率=立体曲环曲折线曲率÷夹角度对应的‘平立倍率值

简化为：Qa?S=Qb?S÷x.a.a..

求立体曲环曲折线半径=平面扇环曲折线半径÷夹角度对应的‘平立倍率值

简化为：Qbr=Qar÷x.a.a..

求立体曲环曲折线曲率=平面扇环曲折线曲率×夹角度对应的‘平立倍率值

简化为：Qb?S=Qa?S×x.a.a..

7 探讨：曲环对扣结构与时空场结构的联系

立体曲环做成后发现，扭量位置相反的两个曲环，只要尺寸合适，可以拼接成一个对应体。这种形状如何定义尚不确定，但其跟有关资料上的时空模拟图类似，因此提供给读者参考。而要做成这样一个对应体，两个曲环的扭量值和夹角度都必须相等，所要计算的是两个曲环内外下口的直径如何做到一致。（具体算法就不再展开了）。

8 探讨：动能大小，场压力值大小，空间加速度快慢与波的夹角度关系

上图可以看出：水波夹角两边的宽度呈明显的不对称性，与实验取得的立体曲环形状类似。且发现动能与水波的夹角度成反比。即：动能越大，产生的水波越高，其夹角度也越小。而根据‘非対称曲折效应原理，曲环夹角度越小，其对应的曲率增加倍率越大。笔者认为水波的形状是动能和场以曲线路径挤出来的。考虑到每个夹角度对应曲率增加倍率不尽相同。所以水波的每个夹角度所对应的动能也应是不同的。而夹角度对应的动能之间和曲率之间的比值应该相同。

如果把这种思考位移到空间，那么动能的大小，也可以在空间反应出来。即动能越大，产生的空间波的夹角度越小。同时空间场对动能的压力就越大，空间加速度也越快。如何理解后面的推断呢？，我们再回到水中观察：动能越大，水波的夹角度就越小，水场反馈给动能的压力就越大，而压力能产生加速度效果。空间场的加速度现象也应是空间场反馈给动能压力的结果。

因此得出：动能大小=波的夹角度小大=动能承受场的压力大小=空间加速度的快慢。

如果这样的理解是正确的。那就可以把波的夹角度变化看成场压力值大小变化，再用立体曲环夹角度对应的曲率净增倍率值来借用于场压力值的度量单位。解释一下：净增倍率值是指在‘平立倍率值上剔除掉基础倍率后的值。

即：动能产生的波夹角在180-150度区间所对应的场压力值=立体曲环夹角在180-150度区间所对应的曲率净增倍率值={180L°×n.Qbr-180L°×n.Qbr×0.004444..倍.×（180L°-Ψ）}÷Ψ÷n.Qbr-1

动能产生的波夹角在150-120度区间所对应的场压力值=立体曲环夹角在150-120度区间所对应的曲率净增倍率值={180L°×n.Qbr×0.8666..-180L°×n.Qbr×0.003333..倍×（150L°-Ψ）}÷Ψ÷n.Qbr-1

动能产生的波夹角在120-90度区间所对应的场压力值=立体曲环夹角在120-90度区间所对应的曲率净增倍率值={180L°×n.Qbr×0.7666..-180L°×n.Qbr×0.002222..倍×（120L°-Ψ）}÷Ψ÷n.Qbr-1

动能产生的波夹角在90-60度区间所对应的场压力值=立体曲环夹角在90-60度间所对应的 曲 净 增 倍 率 值={180L°×n.Qbr×0.7-180×n.Qbr×0.001111..倍×（90L°-Ψ）}÷Ψ÷n.Qbr-1

动能产生的波夹角在60-30度区间所对应的场压力值=立体曲环夹角在60-30度间所对应的 曲 率 净 增 倍 率 值=（180L°×n.Qbr×0.6666..倍）÷Ψ÷n.Qbr-1

然后通过场压力值与动能和空间加速度的换算，得出相应的场压力值所对应的动能、空间加速度分别是多少。

9 结论

‘非对称曲折效应揭示的曲率和夹角度的互换现象，使我们对广义相对论中时空曲率的描述有了更直观的理解——它就是动能和场产生的时空波夹角。同时对研究空间形状和演变原理也提供了新的视角。

关注我研究的朋友认为此物理现象可能跟‘黎曼假设有一定的关联性。我得出的结论是：看不懂这个假设的很多内容，但其描述的‘建立在特殊直线上的非平凡零点又于本实验中的“扭量值”及因其精确扭量比所衍生出的‘平立倍率值有一定对应之处。

参考文献

[1]王仁华，赵宪忠，谢步瀛.平面桁架结构拓扑优化方法研究[J].力学季刊，2010， 31（2）：310-317.

（作者单位：舟山市永达中介所）