逐日动态交通分配模型综述

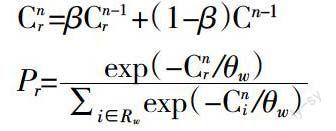
摘 要：交通路网流量是由出行者的路径选择行为所决定，路径选择行为的每日更迭会导致交通流量的变化。逐日动态模型在深刻理解网络流的波动演化过程以及用户均衡状态的可达性上具有重要作用。因此，本文将以往逐日动态模型进行分类并进行相关介绍。

关键词：动态交通分配模型；逐日路径选择；综述

在现实的交通路网中，由于外部因素的干扰以及网络自身的变化，交通流量总是随着时间在不停地变化。在这种情况下，静态的交通分配模型就不足以描述交通流量的震荡演化过程，并且无法探究最后会达到何种形式的用户均衡（确定还是随机）。在过去几十年中，为了深刻理解网络流的波动演化过程以及用户均衡状态的可达性，学者们在逐日动态模型的研究上做出了大量的工作。逐日动态模型不仅是解释交通流量随“天”波动的有效工具，也提供了另一种计算用户均衡的方法。回顾以往的文献，根据基于不同的更新策略，我们可以将基于路径的逐日动态模型分为基于流量更新与基于感知更新的分配模型两类。

1 基于路径的逐日动态模型

1.1 流量更新模型

以流量更新为基础的模型从网络流量的角度切入来描述系统的演化过程。大多数以流量更新为基础的逐日动态模型采用了连续形式。它的路径切换原则是基于每条路径的实际出行成本，并且最后的稳态（平衡状态）是DUE。其中最为经典的模型主要有：

1.1.1 比例切换调整过程Smith（1984）

1.1.2 网络试错调整过程Friesz等（1994）

1.1.3 投影动态系统Nagurney和Zhang（1997）

Yang和Zhang（2009）等人将上述几个固定需求下的模型统一归结为“理性行为调整过程”（RBAP）：随着时间的演化（天数），整个交通网络的整体出行成本在前一天的基础上降低。除了上述这些平衡点收敛到UE的模型外，还有一些其他模型。Jin（2007）在先进先出的规则下建立了FIFO逐日动态系统，其平衡状态不仅仅是DUE，而且是DUE的一个超集。Guo和Liu（2011）在有限理性（BRUE）的框架下，探讨了不可逆的交通路网改变对于整个交通流的影响。有限理性下的逐日动态模型最后的收敛点是一个BRUE集合。尽管BRUE的假设在仿真和实证研究中被广泛应用，但是基于BRUE的动态交通流理论研究还不是很多。

1.2 感知更新模型

基于感知更新的模型把网络交通流的演化看作是出行者对路网出行成本的感知和学习之后的结果。大多数以感知更新为基础的逐日动态模型采用了离散形式。由于整个步长的大小对于系统稳定性的影响很大，离散动力学模型的稳定性分析比连续模型更为复杂。从数学上来说，连续模型就是离散模型的特殊极端情况（时间间隔趋于0），而在模型的标定和用于实际交通流的预测中，连续模型不得不先转化为离散模型。一般假设出行者拥有所有关于交通状况的先前记忆，然后基于这些记忆做出他们的路径选择，一般路径选择采用SUE的分配方式，或者更具体一点，基于LOGIT的路径选择。当感知成本与实际成本发生偏差的时候，出行者会通过一些特定的规则去“矫正”他们对路网的感知成本，“矫正”的参考主要是基于新的出行经历或者是实时发布的交通信息，这样的“矫正”过程我们称之为学习行为。通常而言，感知成本的更新遵从所谓的“指数平滑”规则，也就是说，新的感知成本是之前感知成本与新经历或者实时发布的交通状态的线性组合。这类模型的稳态就是随机用户均衡点。

其中Cn代表出行者的感知成本；？茁表示在对出行成本进行感知时，过去经验所占的比重。Pr表示选择路径的概率。这类模型最早可以追溯到Horowitz（1984），他在只有两个路段的简单路网下，建立了一个离散的动力学系统，而其学习行为的参数（指数平滑的权重）是随着时间而变化的。他的探究表明，学习行为的参数会影响整个交通系统随着时间演化的稳定性。Watling（1999）则在一个更一般化的网络下探究了基于感知成本更新模型的稳定性。Bie和Lo（2010）进一步探究了这类模型的稳定性，并且在吸引域的框架下探究了这类模型的一些性质。

2 基于路段的逐日动态模型

基于路径的模型就是使用路径流量作为变量来对模型进行构建。出行者通过选择连接OD之间的一条路径来完成其整个出行，因此基于这样的表达是很直观的。大部分的逐日动态模型都采用此种方式进行建模，基本建模的思路实际就是不同路径之间的流量通过对出行者行为的不同假设来进行切换。但是这样的模型也存在着一些问题（He等，2010）。

第一，在现实生活中，路径流量就是很难被观测到的数据。大部分的线圈探测器，视频识别等技术能够很方便地观测到路段上面的交通流量，而路径的交通流量需要对整个车辆进行路径的跟踪及推导。第二，基于路径的模型会存在路径重叠的问题，从而影响模型的可靠性。第三，在一个大型的路网中，随着路段数量的增多，路径的枚举量会快速增多，从而导致路径流量之间的切换计算量很大。

从现阶段的文献来看，基于路段的模型数量还是远小于基于路径的模型数量的。He等（2010）最先使用基于路段流量的模型来对出行者的逐日选择进行建模，通过构建一个在可行域（凸域）最小化问题来对出行者的惰性以及灵敏度进行分析，然后通过一个一阶微分方程组来完成路段流量的更新。

其中，？啄是正值参数，它决定了流量的切换速率。y-x提供了路段流量的切换的方向。在给定当前路段流量x的前提下，y通过求解下面的最优化问题得到：

其中，D（x，y）目标交通流模式与当前交通流模式之间的距离，|| y-x||2反映了出行者的惰性。当？姿很小时，用户更倾向于留在当前路段，而当？姿很大时，用户倾向于切换到最短路上以期使出行成本降低。在这之后，Han（2012）等人对其模型性质（诸如不变集和稳定性等）进行了进一步的理论性质分析。He等（2012）人构建了一个“预测-矫正”模型来对明尼苏达双城的I-35W桥坍塌以及修复前后的交通流变化进行分析。出于理论性质分析的方便以及出行者路径切换描述的直观性，学者们更倾向于使用基于路径的模型。而从模型现实应用来看，基于路段的模型更为可取。

3 结论

随着先进交通出行信息系统的发展，出行者可以方便地获取包括实时和历史在内的交通数据。逐日动态模型有很强的灵活性可以将不同的行为假设融入进来，探究不同出行信息发布对于交通流量的影响。后续还可以将拥挤收费、信号控制等拥堵控制手段融入到模型来增强交通系统的表现。

参考文献：

[1] 郭仁拥，黄海军.ATIS环境下交通配流的动态演化模型[J].管理科学学报，2008，02：12-19.

[2] 韩凌辉.多种交通网络条件下出行者的出行选择行为分析[D].北京交通大学，2014.

[3] 张丹.基于逐日动态分配模型的拥挤收费研究[D].西南交通大学，2014.

[4] 张凡.滞后性选择行为下的投影逐日动态分配模型研究[D].西南交通大学，2015.

作者简介：沈旻宇，西南交通大学在读研究生。