部分充填式钢箱-混凝土组合梁的负弯矩区裂缝宽度

莫时旭, 赵剑光, 胥海宁

(1. 广西岩土力学与工程重点实验室， 广西 桂林 541004;2. 桂林理工大学 土木与建筑工程学院， 广西 桂林 541004)



部分充填式钢箱-混凝土组合梁的负弯矩区裂缝宽度

莫时旭1,2, 赵剑光1,2, 胥海宁2

(1. 广西岩土力学与工程重点实验室， 广西 桂林 541004;2. 桂林理工大学 土木与建筑工程学院， 广西 桂林 541004)

摘要：对4根反向加载的部分充填式钢箱-混凝土组合梁进行单调受弯试验，并对影响组合梁负弯矩区裂缝的因素进行分析.根据试验与理论分析，完善考虑混凝土收缩应力的部分充填式钢箱-混凝土组合梁负弯矩区开裂弯矩计算方法.对负弯矩区不同力比的组合梁裂缝宽度试验观测值与各文献计算值进行对比.结果表明：力比是影响组合梁裂缝发展的主要因素，栓钉的布置和钢梁内充填的混凝土对裂缝的发展也有影响.

关键词：钢箱-混凝土； 组合梁； 裂缝； 负弯矩区； 力比

部分充填式钢箱-混凝土组合梁桥是在普通的组合梁桥的基础上，为改善中间支座区受力性能而提出的一种新型连续组合梁桥结构形式.组合梁上部为配筋混凝土翼板，下部为内填了混凝土的钢箱梁，两者通过栓钉连接在一起.钢材和混凝土是组成组合梁桥的主要结构材料，它们既具备良好的力学性能[1]、较高的承载能力[2]、适宜的施工性能和耐久性，同时也具有良好的技术经济效益，能够紧跟现代社会发展的需求.组合梁中的翼缘板受压、钢梁受拉是一种比较有利的受力状态，但是连续组合梁负弯矩区一般都是钢梁受压、翼缘板受拉，所以，组合连续梁桥负弯矩区一般都是带裂缝工作.组合梁翼板出现裂缝会降低结构刚度和强度，影响梁的耐久性和降低使用寿命.因此，要对组合梁负弯矩区的裂缝发展情况进行具体分析，从而控制负弯矩区裂缝的宽度.本文通过对比分析4根部分充填式钢箱-混凝土组合梁在负弯矩区不同力比、栓钉数量和分布、钢箱内全填和部分充填混凝土对翼板裂缝发展的影响，研究组合梁负弯矩区混凝土翼板裂缝的开展规律.

1实验方法

1.1试件的设计

设计了4根部分充填式钢箱-混凝土组合梁(PSCB-1，PSCB-2，PSCB-3，PSCB-4)，并进行对比研究.混凝土翼板参数：组合梁的跨径为4 400 mm；混凝土翼板厚度为120 mm；翼板宽为1 000 mm；翼板混凝土的强度等级均为C40.组合梁截面尺寸：组合梁高为420 mm；钢箱梁截面尺寸为300 mm×120 mm；腹板厚度为6 mm；顶板和底板厚度均为10 mm；钢箱梁采用Q235级钢板焊接而成.试件的材料特性和配筋率,如表1～3所示.

表1　钢材的材料特性

表1～3中：抗剪连接度均为1.0；D/h为直径/厚度；Es为弹性模量；fs为极限强度；fy为屈服强度；fcu

表2 试件参数Tab.2 Parametersoftestspecimens试件号p/%Rd/mmPSCB110.18450PSCB220.36240PSCB330.54180PSCB420.28240表3 试件的材料特性Tab.3 Propertiesoftestspecimens试件编号混凝土翼板fcu/MPa fc/MPa钢箱内填混凝土fcu/MPa fc/MPaPSCB142.126.432.921.8PSCB240.327.932.323.4PSCB341.226.131.222.8PSCB440.828.533.123.1

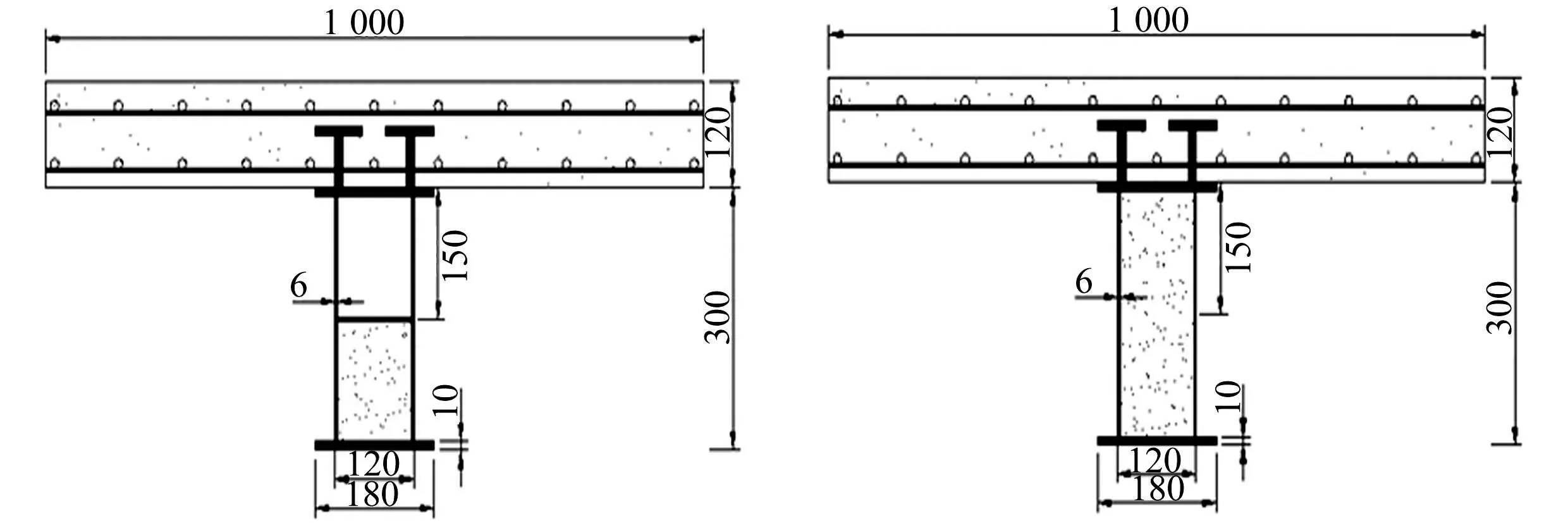
(a) PSCB-1～PSCB-3　　　　　　　　　(b) PSCB-4　　　　图1　组合梁横截面(单位：mm)　Fig.1　Section of the composite beam (unit：mm)

图2　试验装置与加载设备Fig.2　Test setup and loading equipment

为立方体抗压强度；fc为轴心抗压强度；p为配筋率；R为力比；d为栓钉的间距.试件PSCB-1，PSCB-2，PSCB-3钢梁内充填的混凝土为半填充，PSCB-4为全填充.试件具有相同结构尺寸，其截面形状及相关参数，如图1所示.

1.2加载装置

试件的加载装置，如图2所示.采用液压千斤顶进行两点对称式反向加载，施加的荷载通过放置在液压千斤顶上的压力传感器显示，液压千斤顶提供的集中力通过计算跨径为1 400 mm的分配梁分成两个相等的力，经钢梁底板施加给组合梁.荷载按每级10 kN加载，稳定5 min后，进行数据采集和裂缝观测，应变由应变箱采集测得，裂缝宽度由裂缝观测仪测得.同时,在混凝土翼板上画出裂缝的分布和标出对应的荷载值.

2 裂缝的开展及分布规律

2.1力比

文中引用力比值R分析裂缝的发展变化情况[3].由于钢箱内填充了混凝土，采用换算截面法,把组合梁钢梁内填充的混凝土换算成钢材,即

(1)

式(1)中：Ar为组合梁翼板纵向钢筋截面积;As为受压钢梁截面积;Ac为钢梁内填充混凝土截面积;fry,fy分别为纵向钢筋和钢梁的屈服强度;αE为钢材与混凝土的弹性模量之比.

2.2开裂弯矩值

组合梁负弯矩区由于混凝土翼板受拉，在拉应力作用下,翼板上表面很容易出现裂缝.为了更好地探究混凝土翼板开始出现裂缝时的规律，对组合梁的开裂弯矩进行计算.当混凝土翼板与钢梁组合在一起形成组合作用后，混凝土的收缩受到组合梁混凝土翼板内钢筋和钢梁的约束作用.组合梁开裂弯矩不仅受翼板内纵向钢筋和钢梁的影响，也受到翼板混凝土收缩应变的影响.影响混凝土收缩应变的因素很多，除了混凝土本身的特征如集料的种类、水泥、配合比、养护的方法和尺寸外，还受加载期间的湿度、温度和加载龄期等影响.王铁梦[4]观测到混凝土在3个月时的收缩应变为185×10-6，聂建国[5]认为普通混凝土的极限收缩应变为324×10-6,综合参考上述文献，文中混凝土收缩应变取150×10-6.

组合梁开裂弯矩计算时假设[6]：1) 钢材和混凝土为弹性材料，组合梁截面采用换算截面几何特性;2) 平截面假定组合梁中混凝土翼板和钢梁之间的滑移忽略不计.负弯矩区开裂弯矩计算式为

(2)

式(2)中：ft为混凝土的抗拉强度;Wo为组合梁翼板受拉边缘换算截面抵抗矩;σcc为混凝土的收缩应力;γsc为组合梁的截面塑性系数，由组合梁截面特征按照文献[7]的相关公式计算，文中取值为1.8.

表4　开裂弯矩计算值与实测值

2.3裂缝特征

当荷载加载到0.15Pu时，跨中附近开始出现第1条主裂缝；随着荷载增加，在距第1条裂缝119，140，156，170 mm处，试件PSCB-1，PSCB-2，PSCB-3，PSCB-4混凝土翼板上，对称于第1条主裂缝开始依次出现第2，3条主裂缝.当荷载继续增加，不断有新的裂缝产生；当荷载增加到0.4Pu，开始出现横向贯通的主裂缝，裂缝的宽度不断增大、间距不断减小，各贯通裂缝之间仍有新裂缝出现，试件PSCB-1，PSCB-2，PSCB-3，PSCB-4裂缝的最大宽度分别为0.21，0.16，0.11，0.14 mm；当荷载达到0.7Pu后,不再出现新的主裂缝，钢筋开始屈服，试件PSCB-1，PSCB-2，PSCB-3，PSCB-4的混凝土翼板裂缝最大宽度分别为0.38，0.29，0.21，0.26 mm； 随着荷载的增加， 各主裂缝之间出现的次级裂缝较多，试件PSCB-1，PSCB-2，PSCB-3和PSCB-4贯通的主裂缝间距约在190～210 mm之间.各试件混凝土翼板上表面裂缝分布情况,如图3所示.

(a) PSCB-1 (b) PSCB-2

(c) PSCB-3 (d) PSCB-4 图3　试件的裂缝分布Fig.3 Crack distribution of specimens

3结果及分析

力比R是组合梁裂缝宽度的一个重要的影响因素，国内外学者对其进行了研究[8-12].试验结果显示，在荷载相同和钢梁内混凝土充填高度相同时，R越大，裂缝宽度越小；随着荷载的增加，裂缝的发展越慢；而R较小的组合梁，裂缝宽度较大，裂缝发展更快，开裂弯矩越低.由图3可知：试件PSCB-3相比PSCB-1，裂缝的分布较密较细.各试件荷载-最大裂缝宽度曲线的关系，如图4所示.由图4可知：各试件的裂缝宽度在超过0.3 mm后,变化得更快.

组合梁桥主要由钢梁和钢筋混凝土翼板组成，配筋率是影响翼板裂缝的重要因素,但是，充填了混凝土的钢箱梁也是混凝土组合梁的一个重要组成部分，必须综合考虑所选的钢梁和配筋率的相互关系.配筋率较低，力比较小的组合梁，如PSCB-1，当翼板出现裂缝，随着荷载的增加，裂缝的发展较快，裂缝宽度较大，受拉钢筋屈服，但是,混凝土组合梁并没有出现脆性破坏的特征.这是因为具有较好的延伸性的部分充填钢箱梁参与了工作.试件PSCB-3的钢箱完全屈服时，混凝土翼板并没有完全破坏，为了充分利用钢材和混凝土的强度，R不应过大.在较大配筋率的情况下，研究考虑钢箱充填的混凝土提高钢梁的强度和刚度，如试件PSCB-2和PSCB-4.试件PSCB-2和PSCB-4有相同的配筋率，由于钢箱内填充的混凝土情况不同，试件PSCB-4的R较小,裂缝宽度及特征裂缝实测值，如表5所示.表5中：Pu为极限荷载值；P0.2为实测裂缝宽度达到0.2 mm时对应的荷载值；P0.3为实测裂缝宽度达到0.3 mm时对应的荷载值.由表5可知:在翼板裂缝宽度为0.3 mm时，对应P0.3/Pu更大.因此，在控制混凝土翼板裂缝宽度前提下，试件PSCB-4比PSCB-2更能充分利用组合梁的极限强度.

表5　裂缝宽度及特征裂缝实测值

4根试验梁的抗剪连接度均为1.0，但是有不同的栓钉间距.由图3可知:栓钉间距较小的试验梁，其裂缝分布呈八字形特征更加明显，且裂缝发展越慢，裂缝分布更密.试件荷载-钢筋应变关系,如图5所示.由图5可知:当翼板未开裂时，钢筋应变与混凝土相同；而当混凝土翼板开始出现裂缝，钢筋应变突然增大，组合梁进入带裂缝工作阶段.由于栓钉的作用，钢筋的应力通过混凝土翼板传递给了栓钉，引起组合梁栓钉处的混凝土应力集中.因此,栓钉的上方出现裂缝，当裂缝越大，栓钉的作用就越大，限制了裂缝的较大发展.

图4　试件荷载-最大裂缝宽度关系 图5　试件荷载-钢筋应变关系 Fig.4　Load-maximum crack width curves of specimens　　Fig.5　Load-reinforcement strain curves of spcimens

4组合梁翼板裂缝宽度计算

为了计算组合梁负弯矩区的裂缝宽度值，许多学者对此进行了研究.文献[3]，[13]分别提出了裂缝宽度的计算公式;我国《钢结构设计规范》[14]建议,组合梁负弯矩区混凝土翼板的最大裂缝可根据《混凝土设计规范》[15]按轴心受拉进行计算，其计算式为

(3)

(4)

式(3)～(4)中：αcr为构件受力特征系数;ψ为裂缝间纵向受拉钢筋应变不均匀系数;σs为纵向受拉钢筋应力;Es为钢筋的弹性模量;cs为最外层纵向受拉钢筋外边缘至受拉区底边的距离;deq为受拉区纵向钢筋的等效直径;ρte为纵向受拉钢筋配筋率;ftk为混凝土轴心抗拉强度标准值.

文献[12]建议最大裂缝宽度的计算式为

(5)

式(5)中：αcr=1.0;σrk为纵向受拉钢筋应力;la为横向钢筋平均间距;Rp为力比值.

《公路钢筋混凝土和预应力混凝土桥涵设计规范》[16]采用的裂缝宽度计算公式主要建立在因素分析和数理统计基础上，其计算式为

(6)

(7)

式(6)～(7)中：C1为钢筋表面形状系数，对带肋钢筋C1=1.0;C2为考虑荷载长期效应影响系数，C2=1.0;C3为构件性质有关的系数，对轴心受拉构件C3=1.2;σss为纵向受拉钢筋应力;d为纵向受拉钢筋直径;ρ为受拉钢筋配筋率;hf和bf分别为受拉翼板的厚度和宽度;b和ho分别为受拉翼板的有效宽度和高度;As为受拉钢筋截面积.

采用文献[12]、规范[15]和规范[16]的公式，对试件在负弯矩区弹性阶段的最大裂缝宽度进行计算，结果如图6所示.图6中：W为裂缝宽度.由图6可知：规范[15]和规范[16]所得的计算结果与实测值偏差较大，而文献[12]所得的计算值由于综合考虑了钢箱-混凝土组合梁的力比、配筋率、横向钢筋的间距对裂缝宽度的影响，计算结果与实测值相对更接近，对裂缝最大宽度的计算具有一定的参考意义.

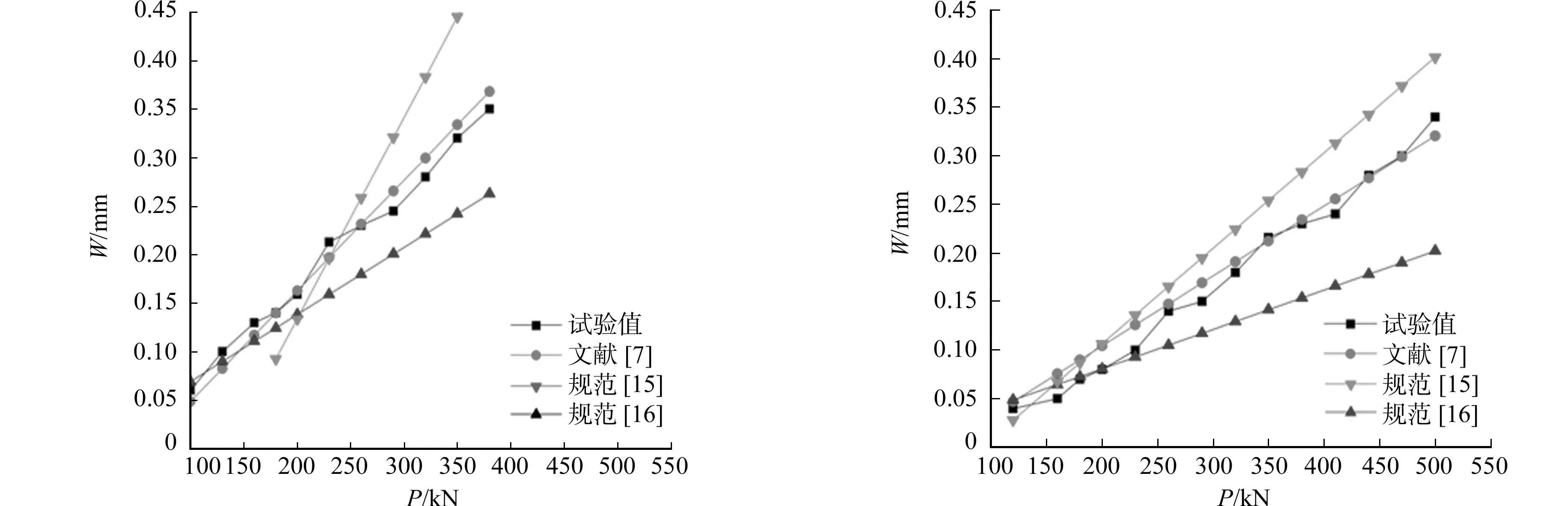
(a) PSCB-1 (b) PSCB-2

(c) PSCB-3 (d) PSCB-4图6　试件裂缝宽度试验值与计算值的比较Fig.6　Comparison between test and numerical crack width of specimens

5结论

1) 当力比较大、配筋率较大时，裂缝的发展趋势缓慢，且宽度较小,分布较密；当力比值较小，裂缝宽度达到0.2 mm时，裂缝发展较快，裂缝的间距较大,裂缝宽度较大.

2) 栓钉间距小的梁，裂缝发展慢，裂缝分布密.

3) 当力比R较大时，钢梁比混凝土翼板钢筋先屈服，为了充分发挥钢材和混凝土的材料特性，可以考虑在钢箱内充填混凝土，以提高钢梁的截面强度和刚度.

4) 相对于普通混凝土梁桥，由于钢梁的约束作用，混凝土的收缩应变对组合梁的开裂弯矩影响较大，力比R越大,开裂弯矩越大.

5) 组合梁翼板裂缝宽度计算应综合考虑组合梁的力比、配筋率、横向钢筋的间距的影响.

参考文献：

[1]莫时旭,周晓冰,周迎春，等.部分充填钢箱-混凝土组合梁受力性能有限元分析[J].华侨大学学报(自然科学版),2015,36(4):455-460.

[2]莫时旭,钟新谷,舒小娟,等.钢箱-混凝土组合梁试验研究与承载能力计算[J].工业建筑,2008，36(增刊1):499-503.

[3]聂建国,张眉河.钢-混凝土组合梁负弯矩区板裂缝的研究[J].清华大学学报(自然科学版),1997,37(6):95-99.

[4]王铁梦.工程结构裂缝控制[M].北京:中国建筑工业出版社,1997:171-190.

[5]聂建国.钢-混凝土组合梁长期变形的计算与分析[J].建筑结构,1997(1):42-45.

[6]周安,刘其伟,戴航.钢-混凝土组合梁中混凝土翼板的收缩应力[J].公路交通科技,2007,24(8):63-66.

[7]胡夏闽.欧洲规范4-钢-混凝土组合梁设计方法(4):组合梁的受弯承载力[J].工业建筑,1995,25(11):42-49.

[8]苏田庆,杨国涛,吴冲.钢箱组合梁混凝土裂缝特征试验[J].中国公路学报,2012,25(5):74-81.

[9]聂建国,樊健生,王挺.钢-压型钢板混凝土组合梁板裂缝的试验研究[J].土木工程学报 ,2002,35(1):15-20.

[10]LEBET J P,NAVARRO M G.Influence of concrete cracking on composite bridge behaviour[C]∥Proceedings of the 5th International Conference, Composite Construction in Steel and Concrete V.New York:ASCE,2006:77-86.

[11]HADIDI R,SAADAGHVAZIRI M.Transverse cracking of concrete bridge decks: State-of-the-art[J].Journal of Bridge Engineering,2005,10(5):503-510.

[12]张彦玲,樊健生,李运生.连续组合梁桥裂缝发展规律分析及裂缝宽度计算[J].工程力学,2011,28(7):84-90.

[13]余志武,郭风琪.部分预应力钢-混凝土连续组合梁负弯矩区裂缝宽度试验研究[J].建筑结构学报,2004, 25(4):55-59.

[14]中华人民共和国建设部.钢结构设计规范: GB 50017-2003[S].北京:中国计划出版社,2003：108-109.

[15]中华人民共和国住房和城乡建设部.混凝土结构设计规范: GB 50010-2010[S].北京:中国建筑出版社,2010：88-96.

[16]中交公路规划设计院.公路钢筋混凝土及预应力混凝土桥涵设计规范: JTGD 62-2004[S].北京:人民交通出版社,2004：58-63.

(责任编辑： 黄晓楠英文审校： 方德平)

Crack Width of Concrete-Partially-Filled Steel Box Composite Beam Under Negative Moment

MO Shixu1,2, ZHAO Jianguang1,2, XU Haining2

(1. Guangxi Key Laboratory of Rock-Soil Mechanic and Engineering, Guilin 541004 , China;2. College of Civil Engineering and Architecture, Guilin University of Technology, Guilin 541004 , China)

Abstract：A flexural test was carried out on four concrete-partially-filled steel box composite beams with reverse loading. The factors that influence the cracks in the negative moment region of the composite beams was analyzed. According to the experimental and theoretical analysis, the method to calculate the cracking moment of the concrete-partially-filled steel box composite beam in the negative moment region considering the concrete shrinkage stress was modified. The test results of crack width in the negative moment region of the composite beams with different force ratios were compared with the calculation values in other references. It is indicated that force ratio is the main factor affecting the development of the crack width of composite beams, while the layout of stud and the concrete filled in the steel beams also influence the crack width.

Keywords：steel box-concrete; composite beams； crack； negative moment region； force ratio

中图分类号：TU 398.9; TU 317.1

文献标志码：A

基金项目：国家自然科学基金资助项目(51168011， 51108109)； 广西岩土力学与工程重点实验室科研基金资助项目(11-CX-05)

通信作者：莫时旭(1964-)，男，教授，博士，主要从事钢-混凝土组合结构的研究.E-mail:478990056@qq.com.

收稿日期：2015-10-24

doi:10.11830/ISSN.1000-5013.2016.03.0352

文章编号：1000-5013(2016)03-0352-06