一种面向WSN时间同步的振荡器模型设计与研究

周春良，陆正球，王　明，屈卫清

（宁波大红鹰学院信息工程学院，宁波　315157）



一种面向WSN时间同步的振荡器模型设计与研究

周春良，陆正球，王明，屈卫清

（宁波大红鹰学院信息工程学院，宁波315157）

摘要：WSN节点采用低成本的晶振，节点之间的频率差异不可避免。该项目讨论频率对耦合振荡器的影响，设计一个适合于WSN时间同步的频率互异耦合振荡器模型。该模型验证振荡器系统在所有条件下都可以达到同步，分析振荡器系统的理论模型，给出系统达到同步的条件。通过多次实验，分析参数对同步的不同影响，验证该模型的可行性。该模型解决振荡器模型因频率不同而出现误差增大的问题，提升整个系统的精度。该模型在经典耦合振荡器基础上，加入频率互异和多跳网络拓扑两个因素，使其更加适用于无线传感器网络。

关键词：频率互异；无线传感网网络；时间同步

0　引言

基于目前的制作工艺，无线传感器模块由于受到温度、电压、计时速度等影响，即便在某一时刻实现了同步，也容易出现时间偏差。因此，时间同步问题一直是无线传感器网络中的研究热点问题之一[1]。

近些年来，学者发现萤火虫在互相靠近的时候，它们发光的频率能够调整到同步，这是一种非常神奇的生物现象。Smith在1935年的文章[2]中对东南亚地区的萤火虫同步闪烁现象进行了生动详细的描写，文中描述了在泰国延绵十几英里的湄公河的河岸边的树上，几乎每片树叶上都存在着近乎完美同步闪烁的萤火虫。这一现象引起了广大学者们的关注，科学家们纷纷对此表示出了极大的兴趣并对其展开研究。而50年之后，John Buck又再次撰文对50年中在这个现象上的相关研究进行了分析，并用两种同步模型Phase-Advance和Phase-Delay对其进行充分的解释说明。在Phase-Advance模型中，他定义了“late sensitivity window”，即最接近萤火虫闪烁的一个时间段，他认为如果萤火虫在“late sensitivity window”中受到光刺激，将立即闪烁。

1990年，Mirollo和Strogatz在Peskin模型的基础上提出一种更加一般化的线性振荡器模型[3]（后简称为M&S模型）。该模型中的自变量x服从函数f（φ）（光滑单调递增上凸函数），相位变量φ满足式子（是同步周期）。

对线性振荡器同步模型的研究主体，从生物学家到数学家、物流学家进而转移到计算机学家，不同类的学者对模型进行研究。由于这一机制应用于计算机网络、神经网络的研究，M&S模型的研究成为今年来的热点。

首先，这些模型都是基于即时耦合的。Ernst等对具有两个延迟的振荡器之间的同步进行了研究分析，并在具有延迟的多个振荡器系统进行仿真实验。他们得出的结论是，如果在实验中采用负耦合（inhibitory couping，即ε＜0），系统仍然能够达到同步。

其次，M&S模型的全互联的网络拓扑也在模型应用范围上设置了限制，特别是多跳无线网络中。Dennis 和Wang证明了M&S模型只允许在邻居通信的前提下能够达到同步。

最后，由于采用廉价的单片机作为无线传感器网络的节点处理器，故其无法处理M&S模型的非线性的状态函数。Werner-Allen等针对这一现状运用了一阶泰勒展开进行了近似，并验证了该模型在特定的条件下都能达到同步的情况，但该条件过于的理想化，不适用于在现实生活中的应用。

1　改进同步算法

1.1改进模型描述

令振荡器i的频率fi对应的周期为Ti。假设所有振荡器的频率为闭区间[a，b]上的独立同分布的随机变量，并且具有连续的概率密度函数。

由于周期的不同使得振荡器在同一时间内对于的相位不同，故需要对不同振荡器之间相位变量的换算关系进行定义。对于两个振荡器A和B，其频率为fA，fB周期为TA，TB。假设在某一时刻B的相位为φB，其对应于A的相位φA定义为：

将耦合振荡器建模成“集成-激发”的振荡器网络。且振荡器都按照式1所定义的线性关系进行演化运算。当φi=1时，激发第i个振荡器，并且跳回到状态φi= 0。因为振荡器的频率不同，所以不能保证振荡器都这着相同的相位，故必须重新对振荡器之间的同步定义。

频率互异振荡器的同步：定义两个振荡器A和B同步，当且仅当它们的相位总是同时回到0点，即：

频率互异振荡器的瞬时同步：定义两个振荡器A 和B瞬时同步，如果它们在某时刻相位同时回到0点，即φA|t=φB|t=0。其中，X|t为振荡器X在t时刻的相位。

1.2同步条件与同步证明

由于频率的差异不同，对振荡器的的同步产生的两种情况的影响：第一、即使频率不同的振荡器达到同步状态，它们的相位也不能一直保持同步，只有在相位等于0是才彼此相等，即瞬时同步。第二、对于频率不同的振荡器，即使达到瞬时同步，也可能由于频率差异而失去同步。因此，振荡器的同步必须在满足某种约束条件下才能保持同步。因此，项目组假定振荡器同步的条件，并验证如果该条件满足，同步将一直被保持。

（1）频率互异振荡器保持同步的条件

两个频率互异振荡器的同步保持同步的条件：对于两个振荡器A和B，当且仅当这两个振荡器将会保持同步的状态。由于A的周期更短，因此其在t=TA时刻激发，并且瞬间之后其相位回到0点。由于系统之间的耦合作用，B的相位增加到：

如果A和B之间的同步保持不变，则必须满足式4，来保证B也激发并且相位能够回到0点，反之定理同样。

（2）频率互异振荡器保持瞬间同步的条件

振荡器达到瞬间同步时，它们的频率必须要不相同，即fA≠fB。由式（4）可得，（fB/fA-1）≠0。另外，对于任意ε∈（0，1），有（fB/fA-1）（1+ε）≠0。因此，得知RB|A（φB）＞φB，当和RB|A（φB）＜φB，

综上所述，振荡器系统在满足式（5）的条件下，φ趋向0或者1。在上述情况下，两个振荡器系统会达到瞬间同步。

2　实验与结果分析

2.1实验环境

项目组组建了基于GAINS-3的WSNs测试平台，并在该平台上进行验证上文所述的算法。如下图1所示，该平台由若干个GAINS-3节点组成，每个节点连接一个以太网模块，通过以太网模块再连接到交换机上。

2.2实验步骤

仿真实验假设振荡器的数目为n个，耦合强度为ε。仿真实验在大整数10000000附近产生随机数，相位ε被设置在区间[0，1]之间的一个随机数。仿真分为若干个周期，每个周期先找到下一个被激发的振荡器；等待进入激发状态，根据耦合强度调整振荡器自己的相位，最后将所有的振荡器合并为一个系统，重新调整耦合强度。不断进行循环，直到只剩下一个振荡器组，系统就安全进入稳定的同步状态。

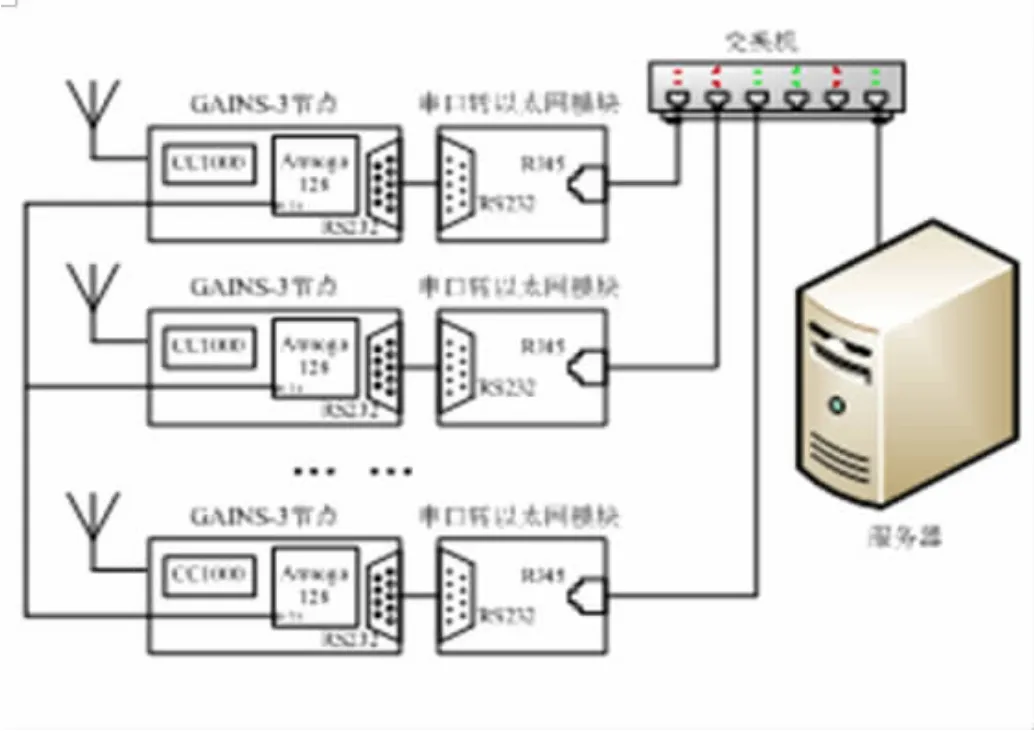
图1　ZigBee测试平台系统结构

图2表示为50个振荡器在相位为0时，相位随周期K的变换过程，该实验取φ为0到1.0中的67个随机数时的情况，从上图可以得出随着运作周数的增加，振荡器逐步聚集成同步振荡的系统，且最终达到完全同步的状态。从实验得出，对于相同的φ，其达到同步状态的时间随着周期的增加而增加。

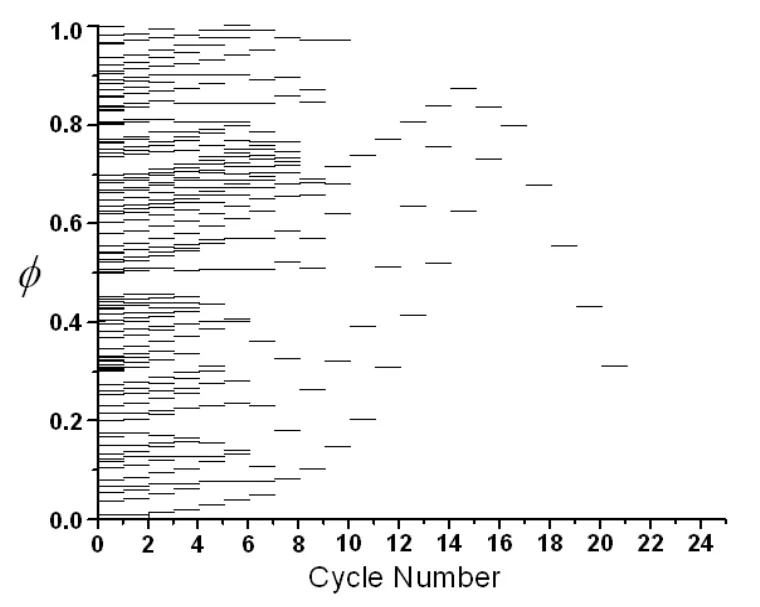
图2　不同下同步所需周期数随振荡器数目

图3为不同ε情况下，同步所需周期数随着振荡器数目的变换情况。从实验堪，在固定的振荡器数目情况下，ε越大同步周期越小，这时因为ε不断增大，振荡器会更快趋于同步；对于固定的ε，随着振荡器数目的增加，越容易聚集成同步状态的振荡器组。这是由于增加了振荡器的ε，因此系统也更会趋于同步。

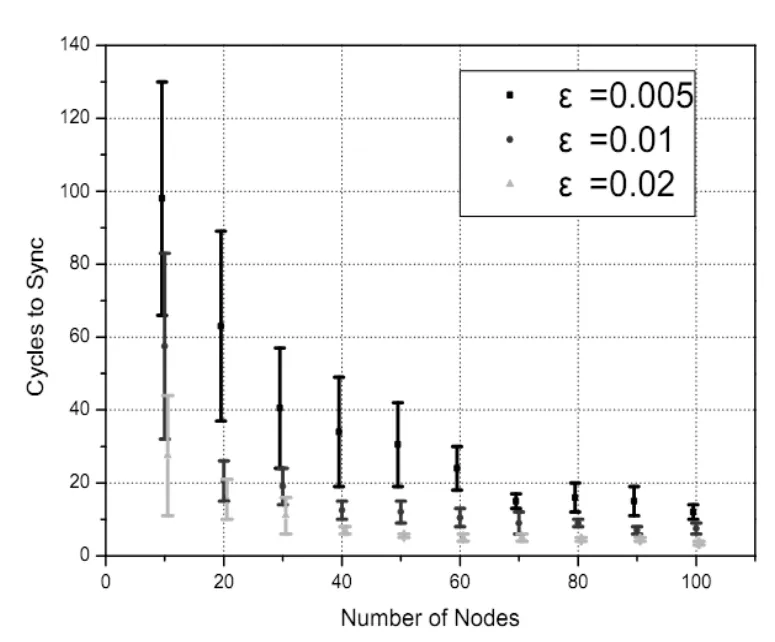
图3　不同ε下同步所需周期数随振荡器数目的变化情况

3　结语

WSN节点由于采用的晶振是低成本的，在节点之间频率的差异还是存在着问题。项目组在振荡器模型的频率同步进行了深入的研究，从理论上验证了该模型的同步性，并通过仿真实验进行了进一步的验证。对于瞬间的同步情况，项目组验证了系统在不满足瞬时同步条件时所组成的系统勒贝格测度为0。对于满足同步保持条件的频率互异的振荡器系统，项目组验证了其几乎在所有的条件下均能够达到瞬间同步。

参考文献：

[1]徐朝农. M＆S模型及其在无线多跳网络时间同步中的应用[J].计算机应用与软件，2010，11（2）.

[2]王世军.同步精度稳定的多跳无线传感器网络时间同步算法[J].计算机应用，2007，12（1）.

[3]徐朝农，徐勇军.无线传感器网络时间同步新技术[J].计算机研究与发展，2008，45（1）.

陆正球（1982-），男，浙江宁波人，硕士，讲师，研究方向为传感器网络

屈卫清（1969-），女、浙江台州人，硕士、副教授，研究方向为传感器网络

王明（1968-），男，江西高安人，硕士、教授，研究方向为网络协议分析

Design and Research on an Oscillator Model Oriented at WSN Time Synchronization

ZHOU Chun-liang，LV Zheng-qiu，WANG Ming，QU Wei-qing
（College of Information Engineering，NingboDahongying University，Ningbo 315157）

Abstract：The WAN's nodes adopt low cost crystal oscillator, so the frequency difference between nodes is inevitable. Discusses the frequency influence to coupled oscillator, and designs a frequency different coupled oscillator model which is suitable for time synchronization. Themodel validates that the oscillator system can realize the synchronization under any conditions and analyze the theory model of oscillator and give the condition of synchronization. By simulation experiment, analyzes the influence of parameters’to synchronization and validates the model feasibility. The model solves the problem that the error will be lager because of the different frequency of classic oscillator model, and improves the system’s precision. The model adds two factors of frequency different and multi hop network topology based on classic coupled oscillator and makes it more suitable for WSNs.

Keywords：Different Frequency; WSN; Time Synchronization

收稿日期：2016-01-17修稿日期：2016-03-20

作者简介：周春良（1982-），男，浙江宁波人，硕士，讲师，研究方向为传感器网络

文章编号：1007-1423（2016）10-0003-04

DOI：10.3969/j.issn.1007-1423.2016.10.001

基金项目：浙江省教育厅科研课题（No.Y201432666）