基于q近邻的不完备数据三支决策聚类方法*

苏　婷，于　洪重庆邮电大学 计算智能重庆市重点实验室，重庆 400065



基于q近邻的不完备数据三支决策聚类方法*

苏婷，于洪+
重庆邮电大学 计算智能重庆市重点实验室，重庆 400065

SU Ting,YU Hong.Three-way decision clustering algorithm for incomplete data based on q-nearest neighbors.Journal of Frontiers of Computer Science and Technology,2016,10(6):875-883.

CNKI网络优先出版:2015-09-28,http://www.cnki.net/kcms/detail/11.5602.TP.20150928.1712.010.html

摘要：聚类是数据挖掘的重要技术之一，在许多实际应用领域，由于数据获取限制，数据误读，随机噪音等原因会造成大量的缺失数据，形成数据集的不完备性，而传统的聚类方法无法直接对这类数据集进行聚类分析。针对数值型数据，提出了一个基于三支决策的不完备数据聚类方法。首先找到不完备数据对象的q个近邻，使用q个近邻的平均值填充缺失的数据；然后在“完备的”数据集上使用基于密度峰值的聚类方法得到簇划分，对每个簇中含有不确定性的数据对象，使用三支决策的思想将其划分到边界域中。三支决策聚类结果采用区间集形式表示，通常一个簇被划分成正域、负域和边界域部分，可以更好地描述软聚类结果。在UCI数据集和人工数据集上的实验结果展示了算法的有效性。

关键词：不完备数据；三支决策聚类；q近邻

ISSN 1673-9418CODEN JKYTA8

Journal of Frontiers of Computer Science and Technology

1673-9418/2016/10(06)-0875-09

E-mail:fcst@vip.163.com

http://www.ceaj.org

Tel:+86-10-89056056

1　引言

聚类是数据挖掘与机器学习中一个重要的研究领域，在商务智能、图像识别、生物学等领域中有广泛的应用[1]。然而，由于数据获取限制，数据误读，随机噪音等原因会造成大量的缺失数据，这些缺失的数据给数据分析带来了巨大的困难。例如，在商业数据库中，一些涉及隐私的数据，比如收入和年龄等，顾客不愿意将这些数据提供给商场，这就造成了某些商业数据的缺失，重新获取这些数据需要花费较高的代价甚至没有办法获取。作为机器学习领域基准数据库的UCI数据集中超过40%的数据库都含有缺失数据。这种缺失某些数据值的数据集，一般称为不完备数据集。一般而言有3种数据缺失机制，根据Rubin等人[2-3]的分类法，数据的缺失机制被分为完全的随机缺失（missing completely at random）、随机缺失（missing at random）和不随机缺失（not missing at random）。由于数据的缺失，传统的聚类算法不能直接使用在不完备数据集上，因此对不完备数据进行聚类的问题是聚类分析研究中一个具有挑战且不容忽视的难题。

为了解决不完备数据的聚类问题，许多新的聚类策略在已有聚类方法的基础上被提出。Hathaway 和Bezdek[4]在模糊C均值聚类（fuzzy C-means，FCM）算法的基础上提出了4种具体的不完备数据聚类方法：完整数据策略（whole-data strategy）、部分距离策略（partial distance strategy）、最优填补策略（optimal completion strategy）和最近簇中心策略（nearest prototype strategy）。Sarkar等人[5]提出距离估计策略（distance estimation strategy）的模糊C均值方法，认为在计算隶属度时得到不完备数据对象与簇中心之间的距离要比得到缺失的属性值更重要。Di Nuovo[6]将不完备数据的模糊C均值方法使用在心理学研究数据集中。Aydilek等人[7]提出了一种支持向量机和遗传算法混合的方法来估计缺失数据和最优化FCM算法中的参数。为了充分利用类簇分布和数据集信息来处理不完备数据，Himmelspach等人[8]考虑了簇分散度，基于簇分散度为缺失数据估值提出了一个新的隶属度方法。

国内学者也在模糊C均值聚类算法的基础上，提出了几种新的不完备数据的聚类方法。Jia等人[9]按照不完备数据集中数据的缺失率采用不同的聚类策略。Li等人[10]在OCS-FCM算法基础上引入了权重的思想，算法可以同时得到聚类结果和属性重要性。随后文献[11]将遗传算法与FCM算法相结合，在得到最终聚类结果的同时得到对缺失属性值的最佳估计值。

近年来，最近邻方法被广泛使用在不完备数据分析中。Doquire等人[12]使用基于互信息的最近邻方法估计不完备的数据。Van Hulse等人[13]在完备数据以及被填充的不完备数据中寻找未填补的不完备数据的q个近邻，最后使用近邻的均值填补缺失的数据。Li等人在文献[14]中使用区间的形式来估计缺失的属性值，区间端点为不完备数据近邻的最大和最小值，然后改进了FCM算法，使其运用在以区间形式表示的数据集上来得到聚类结果。

此外，除了模糊聚类算法外，还有其他方法用于不完备数据的聚类。文献[15]将不完备数据填补后直接使用在近邻传播方法中获得聚类结果。Abd-Allah等人[16]没有直接对缺失的属性值进行填补，而是提出了一种计算含有缺失属性值的数据对象在任意一维上的相似度，然后将改进的相似度计算方法运用到Mean Shift算法上解决了不完备数据的聚类问题。在作者前期的工作中，考虑了属性重要性和属性的缺失情况，提出了一个基于三支决策的不完备数据聚类方法[17]。

在实际生活中，信息具有不确定性或不完整性。这直接导致无法做出决定：接受或拒绝。在这种情况下，人们常常不自觉地使用三支决策，即三支决策理论是传统二支决策理论的扩展[18]。三支决策理论是在粗糙集和决策粗糙集研究中提出的，其主要目的是为粗糙集3个域提供合理的语义解释。粗糙集模型的正域、负域和边界域可以解释为接受、拒绝和不承诺3种决策结果。

在已有的聚类研究中，一个数据对象确定地属于一个簇或者不属于一个簇，这是一个二支决策结果。一个类簇由两个域组成，即正域和负域，正域中的数据对象确定属于这个簇，负域中的数据对象确定不属于这个类，通常使用一个单一的集合来表示一个簇。在三支决策聚类中，一个簇由3个区域组成，即正域、负域和边界域，正域中的数据对象确定属于这个簇，边界域中的数据对象可能属于这个簇，负域中的数据对象确定不属于这个簇。Yao[18]概述了三支决策的理论，并指出可以在多值逻辑和集合论的推广中描述和解释三支决策，包括区间集、粗糙集、决策粗糙集、模糊集以及阴影集。因此，在前期的工作中，提出了使用区间集[19]来表示三支决策聚类结果，使用一对称为上界与下界的集合，来表示一个类簇。属于下界的对象表示其确定属于类簇；不属于上界的对象表示其确定不属于类簇，属于上界与下界之间的对象表示其可能属于类簇[20]。

不完备数据本身具有一定的不确定性，缺少有效的决策信息，因此将三支决策思想使用在不完备数据的聚类中是合理的。针对数值型数据，本文提出了一个基于q近邻的不完备数据三支决策聚类方法。本文后续部分组织如下：第2章介绍相关理论；第3章是对聚类算法的详细介绍；第4章通过在UCI数据集及人工数据集上的实验展示算法的性能；第5章是结论与对未来工作的展望。

2　基本理论

下面首先定义本文的研究对象，即不完备信息系统，然后给出三支决策聚类结果的区间集描述方法，最后对新算法中使用的基于密度峰值的方法[21]进行简要介绍。

2.1不完备信息系统

2.2聚类的区间集表示

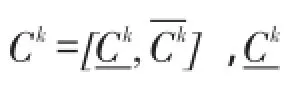
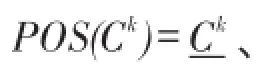
根据以上类簇的表示方法，可以得到聚类结果的区间集描述形式如下：

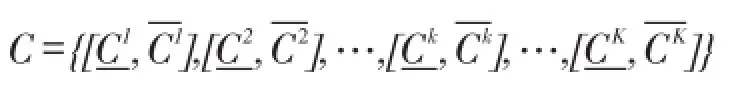
在使用区间集表示聚类结果时，区间集满足一些重要性质：

性质（1）表明任何一个类簇不能为空；为了使类簇具有物理含义，性质（2）表明全集U的任何一个数据对象至少在一个簇的上界中。

2.3基于密度峰值的快速聚类方法

基于密度峰值的聚类方法是近期发表在Science上的文章[21]，该算法的基本思想非常的新颖而简单，为聚类算法的设计提供了一种新的思路。

算法基于这样的假设：类簇中心被具有较低局部密度的邻居点包围，且与更高密度点之间的距离相对较大，也就是说簇中心的密度大，并且簇中心点之间的距离大。通过这个简单的假设，可以找到类簇中心。因此，为了寻找类簇中心，对于每一个数据点xi，需要计算两个量，即点的局部密度ρi和该点到具有更高局部密度的点的最近距离δi，而这两个值都取决于数据点间的距离Dist(xi,xj)，具体定义如下。

定义1（局部密度）数据对象xi的局部密度ρi是与xi的距离小于截断距离阈值的点的个数，计算公式如下：

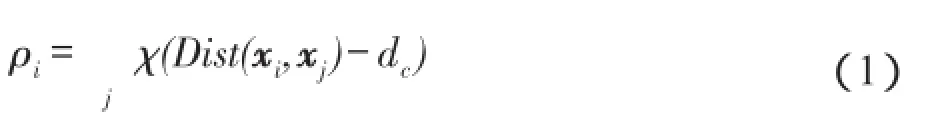
其中，当x<0时，χ(x)=1，否则χ(x)=0；dc为截断距离，文中dc选取的是经验值。

定义2（数据对象与高密度点的最小距离）数据对象xi与所有密度更高点之间距离的最小值为δi，具体计算公式如下：

当数据对象xi的密度最大时，距离δi是对象xi与数据集中其他对象之间距离的最大值，即 δi=

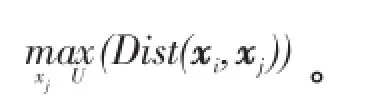
得到类簇中心后，其他非簇中心的样本点依据局部密度从高到低排列，并依次划分它们到距离最近且密度更高的样本点所属的类别中。

3　基于q近邻的不完备数据三支决策聚类算法

本文首先采用基于q近邻的方法对不完备数据集中缺失的数据进行填充；然后在“完备”的数据集上使用基于密度峰值的聚类方法得到初步的聚类结果。通过以上过程大部分的数据会被正确地划分，而处在类簇边缘部分的数据对象的归属可能存在一定的不确定性，因此接下来使用三支决策的方法对每个簇中的数据对象进行分析，将含有不确定性的数据对象划分到边界域中。

3.1基于q近邻的不完备数据填充方法

最近邻（nearest neighbor，NN）规则已广泛应用于模式识别领域的不完备数据估算中。数据对象与其q个近邻具有很高的相似性，同样不完备数据对象与其近邻数据对象应具有相同或相似的属性值，因此可以将这一思想使用在不完备数据的填充中，利用q个邻居的属性值得到缺失数据的合理估值。选择数据对象的q个最近邻居要比只选择最近的数据对象更具有鲁棒性。

基于q近邻的不完备数据填充方法使用不完备数据对象的q个近邻的平均值填充缺失的属性值。因此首先需要找到不完备数据对象的q个近邻，然而由于一些属性值的缺失，不完备数据对象之间的距离不能使用传统的欧氏距离公式计算得到。本文使用局部欧氏距离公式进行计算[4]，该公式只使用两个数据对象均没有缺失的那些属性来计算它们之间的距离，具体公式如下：

当找到不完备数据的q个近邻后，缺失的数据可以由没有缺失该属性值的近邻数据对象的平均值求得。可能会出现极端情况，即q个近邻在某一维属性的数据全部缺失，无法对缺失的数据进行填补时，则使用随机数进行填补。然而，对于随机缺失的数据集，这种情况几乎不会发生。

3.2三支决策聚类

经过填充后“完备”的数据对象可以由基于密度峰值的聚类算法得到聚类结果，但是由于不完备数据本身的不确定性，以及对缺失数据估值可能带来的不确定性，会造成一些数据对象成为噪声点，同时还有一些数据对象可能处在类簇的边缘部分，对它们进行确定的划分会给聚类带来一定的误差。

根据以上分析，利用三支决策的思想对聚类结果进行分析，将含有不确定性的数据对象划分到相应簇的边界域部分。划分思想是类簇的边界部分数据对象的密度要小于簇内部数据对象的密度。具体的分析方法是，首先计算每个簇中数据对象的平均密度，对于密度小于平均值的数据对象，如果它的截断距离dc范围中含有属于其他簇的数据对象，则将该数据对象划分到该簇的边界域部分。

形式化表示是，首先计算类簇Ci的平均密度-ρi，计算公式如下：

3.3算法流程

基于q近邻的不完备数据三支决策聚类方法描述如下：

输入：不完备数据集U={x1,x2,…,xn,…,xN}，近邻个数q，阈值dc，类簇个数K。

输出：三支决策聚类结果。

步骤1找到每个不完备数据对象的q个近邻；

步骤2使用近邻中不缺失属性值的平均值填充不完备数据相应属性上的缺失值；

步骤3按照2.3节介绍的方法，计算每个数据对象的局部密度ρi和距离δi，并找到K个簇中心；

步骤4每个非簇中心的数据对象，按照局部密度从高到低的顺序，依次划分它们到距离最近的更高密度样本点所属的类中；

步骤5将每个簇中局部密度小于簇的平均密度并且近邻中包含其他簇对象的数据对象划分到相应簇的边界域部分，得到最终的三支决策聚类结果。

4　实验分析

本文将给出在人工数据集和UCI数据集[22]上的实验结果来验证算法的性能。不完备数据集必须满足以下条件：（1）数据集中每个数据对象至少有一个属性值；（2）数据集中任何一个属性都必须有至少一个完整的值。以上条件确保了数据集中每一个数据对象以及所有的属性值是有意义的。

设λ={λ1,λ2,…,λk,…,λK}是数据集真实的聚类结果，C={C1,C2,…,Ck,…,CK}是本文方法得出的聚类结果。准确率将用来评估聚类结果的质量。设θk是簇Ck中正确划分的数据对象的个数，其中包括正确划分的边界域的数据对象，则聚类结果的准确率计算公式如下：

其中，N是数据对象的总数；K是类簇的个数。准确率与聚类结果的质量成正比。

实验1首先用一个二维人工数据集Aggregation来直观地展示算法的效果，该数据集包含788个数据对象，7个类。数据集按照5%、10%的缺失率随机产生缺失数据。在随机缺失的数据集上运行本文方法，近邻个数q=10，dc=2。图1是原始Aggregation数据集；图2是当Aggregation数据集含有5%的缺失数据时，使用本文方法对缺失数据填充后的聚类结果；图3是当Aggregation数据集含有10%的缺失数据时，使用本文方法对缺失数据填充后的聚类结果。图2和图3中，使用不同的标记将每个类簇中边界域的数据对象与正域的对象进行区分。

Fig.1　Original dataset ofAggregation图1　Aggregation数据集

Fig.2　Clustering result ofAggregation with 5%missing图2　Aggregation数据集缺失率为5%的聚类结果

通过观察图2和图3，当数据集含有5%和10%的缺失数据时，数据集中的数据对象可以较为准确地被划分到所属的簇中，并且算法可以较好地识别出位于边界域中的数据对象，填充后数据的分布基本没有大的变化，只有少量数据对象填充不正确。因此，实验1说明本文方法对不完备数据聚类是有效的，大多数缺失数据能够被近似地填充，并被正确划分到相应的簇中。同时，本文方法可以将本身位于簇的边界和少量没有被正确填充的数据对象划分到簇的边界域部分。

Fig.3 Clustering result ofAggregation with 10%missing图3　Aggregation数据集缺失率为10%的聚类结果

实验2此外，为了进一步验证本文方法的性能，在UCI数据集和人工数据集上使用准确率和运行时间对算法进行评估，并与文献[4]中的OCS-FCM方法进行对比。文献[4]是不完备数据聚类问题研究中较为经典的文献，目前大多数基于模糊C均值的不完备数据聚类方法都是在文献[4]的基础上得到的。表1给出了这些数据集的大小、属性个数和类簇个数。

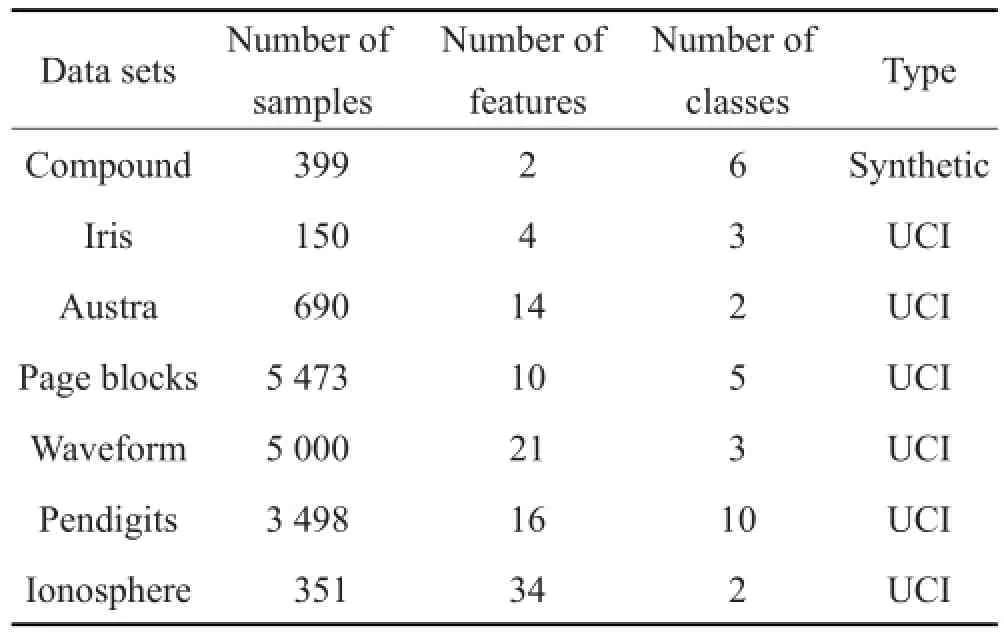
Table 1　Data sets used in experiment表1　实验中使用的数据集

在实验中，首先对数据集按照5%、10%、15%和20%的缺失率随机生成缺失数据构造不完备数据集，每个缺失率下都对应生成10个不同的不完备数据集，以避免缺失数据的分布情况对算法性能的影响。实验参数dc选择经验值，数据对象的近邻个数选择经验值q=10，将数据集在每个缺失率下的10组实验结果的准确率以及运行时间的平均值和方差记录在表2中。

从表2中记录的实验结果可以看出，除了Iris数据集缺失率为10%和20%时的情况，本文方法的准确率均要高于对比方法。分析后不难发现：对比方法是基于模糊C均值的方法，易受到初始簇中心的影响，并且在非球形分布的数据集上难以取得较好的结果；本文基于密度的聚类方法能够处理任意形状的簇结构。因此，本文方法的准确率高于对比方法。同时，在Page blocks数据集上，本文方法的准确率要明显高于对比方法，通过分析数据集的数据分布情况，发现Page blocks数据集不同簇中数据对象的个数相差很大，因此该实验结果还可以说明本文方法在簇中数据对象的个数相差很大时可以取得较好的效果。在大多数情况下，当数据集中数据的缺失率越高时，聚类结果的准确率越低。因为缺失率越高，近邻信息的可靠性下降，不完备数据填充的准确度也会下降，直接导致了聚类算法性能下降。表2的实验结果还说明本文方法的运行时间要高于对比方法，需要在今后的工作中改进。

Table 2　Experiment results on synthetic and UCI data sets表2　人工数据集和UCI数据集上的实验结果

5　结束语

本文提出了一种基于q近邻的不完备数据三支决策聚类方法。方法使用不完备数据的q个近邻的平均值填充缺失的数据，然后使用基于密度峰值的聚类方法在“完备”的数据集上得到聚类结果，最后使用三支决策方法将每个簇中具有不确定性的数据对象划分到相应簇的边界域部分。本文方法的准确率较好，但运行时间较长，并且存在一些不足之处，例如如何较好地选择q值，当数据集的缺失率较高时，q近邻填充方法性能下降，在今后的工作中会逐步完善这些缺陷。

References:

[1]Jain A K.Data clustering:50 years beyond K-means[J].Pattern Recognition Letters,2010,31(8):651-666.

[2]Rubin D B.Inference and missing data[J].Biometrika, 1976,63(3):581-592.

[3]Little R J A,Rubin D B.Statistical analysis with missing data[M].Hoboken,USA:John Wiley&Sons,2014.

[4]Hathaway R J,Bezdek J C.Fuzzy C-means clustering of incomplete data[J].IEEE Transactions on Systems,Man,and Cybernetics:Part B Cybernetics,2001,31(5):735-744.

[5]Sarkar M,Leong T Y.Fuzzy K-means clustering with missing values[C]//Proceedings of the American Medical Informatics Association Symposium.Bethesda,USA:AMIA,2001: 588-592.

[6]Di Nuovo A G.Missing data analysis with fuzzy C-means: a study of its application in a psychological scenario[J].Expert Systems withApplications,2011,38(6):6793-6797.

[7]Aydilek I B,Arslan A.A hybrid method for imputation of missing values using optimized fuzzy C-means with support vector regression and a genetic algorithm[J].Information Sciences,2013,233:25-35.

[8]Himmelspach L,Conrad S.Fuzzy clustering of incomplete data based on cluster dispersion[C]//LNCS 6178:Computational Intelligence for Knowledge-Based Systems Design, Proceedings of the 13th International Conference on Information Processing and Management of Uncertainty,Dortmund,Germany,Jun 28-Jul 2,2010.Berlin,Heidelberg: Springer,2010:59-68.

[9]Jia Zhiping,Yu Zhiqiang,Zhang Chenghui.Fuzzy C-means clustering algorithm based on incomplete data[C]//Procee dings of the 2006 International Conference on Information Acquisition,Weihai,China,Aug 20-23,2006.Piscataway, USA:IEEE,2006:601-604.

[10]Li Dan,Zhong Chongquan,Li Jinhua.An attribute weighted fuzzy C-means algorithm for incomplete data sets[C]//Proceedings of the 2012 International Conference on System Science and Engineering.Dalian,China,Jun 30-Jul 2, 2012.Piscataway,USA:IEEE,2012:449-453.

[11]Li Dan,Gu Hong,Zhang Liyong.Ahybrid genetic algorithmfuzzy C-means approach for incomplete data clustering based on nearest-neighbor intervals[J].Soft Computing,2013,17 (10):1787-1796.

[12]Doquire G,Verleysen M.Feature selection with missing data using mutual information estimators[J].Neurocomputing, 2012,90:3-11.

[13]Van Hulse J,Khoshgoftaar T M.Incomplete-case nearest neighbor imputation in software measurement data[J].Information Sciences,2014,259:596-610.

[14]Li Dan,Gu Hong,Zhang Liyong.A fuzzy C-means clustering algorithm based on nearest-neighbor intervals for incomplete data[J].Expert Systems with Applications,2010,37 (10):6942-6947.

[15]Lu Cheng,Song Shiji,Wu Cheng.Affinity propagation clustering with incomplete data[C]//Computational Intelligence, Networked Systems and Their Applications:Proceedings of the International Conference of Life System Modeling and Simulation,and International Conference on Intelligent ComputingforSustainableEnergyandEnvironment, Shanghai,China,Sep 20-23,2014.Berlin,Heidelberg: Springer,2014:239-248.

[16]AbdAllah L,Shimshoni I.Mean shift clustering algorithm for data with missing values[C]//LNCS 8646:Proceedingsof the 16th International Conference on Data Warehousing and Knowledge Discovery,Munich,Germany,Sep 2-4,2014. Berlin,Heidelberg:Springer,2014:426-438.

[17]Yu Hong,Su Ting,Zeng Xianhua.A three-way decisions clustering algorithm for incomplete data[C]//LNCS 8818: Proceedings of the 9th International Conference on Rough Sets and Knowledge Technology,Shanghai,China,Oct 24-26,2014.Berlin,Heidelberg:Springer,2014:765-776.

[18]Yao Yiyu.An outline of a theory of three-way decisions[C]// LNCS 7413:Proceedings of the 8th International Conference on Rough Sets and Current Trends in Computing, Chengdu,China,Aug 17-20,2012.Berlin,Heidelberg:Springer,2012:1-17.

[19]Yao Yiyu,Lingras P,Wang Ruizhi,et al.Interval set cluster analysis:a re-formulation[C]//LNCS 5908:Proceedings of the 12th International Conference on Rough Sets,Fuzzy Sets,Data Mining and Granular Computing,Delhi,India, Dec 15-18,2009.Berlin,Heidelberg:Springer,2009:398-405.

[20]Yu Hong,Wang Ying.Three-way decisions method for overlapping clustering[C]//LNCS 7413:Proceedings of the 8th International Conference on Rough Sets and Current Trends in Computing,Chengdu,China,Aug 17-20,2012. Berlin,Heidelberg:Springer,2012:277-286.

[21]Alex R,Alessandro L.Clustering by fast search and find of density peaks[J].Science,2014,344(6191):1492-1496.

[22]UCI machine learning repository[EB/OL].[2015-05-16]. http://archive.ics.uci.edu/ml/.

SU Ting was born in 1990.She is an M.S.candidate at Chongqing University of Posts and Telecommunications. Her research interests include data mining and three-way decision theory.

苏婷（1990—），女，新疆伊宁人，重庆邮电大学硕士研究生，主要研究领域为数据挖掘，三支决策理论。

YU Hong was born in 1972.She received the Ph.D.degree from Chongqing University in 2003.Now she is a professor at Chongqing University of Posts and Telecommunications,and the member of CCF.Her research interests include rough sets,three-way decisions,intelligence information processing,Web intelligence and data mining.

于洪（1972—），女，重庆人，2003年于重庆大学获得博士学位，现为重庆邮电大学教授，CCF会员，主要研究领域为Rough Sets理论，三支决策理论，智能信息处理，Web智能，数据挖掘。

+Corresponding author:E-mail:yuhong@cqupt.edu.cn

文献标志码：A

中图分类号：TP181.1

doi:10.3778/j.issn.1673-9418.1506050

Three-Way Decision Clustering Algorithm for Incomplete Data Based on q-Nearest Neighbors*

SU Ting,YU Hong+
Chongqing Key Laboratory of Computational Intelligence,Chongqing University of Posts and Telecommunications,
Chongqing 400065,China

Abstract:Clustering is a common technique for data analysis,and has been widely used in many practical areas. However,in many practical applications,there are some reasons to cause the missing values in real data sets such as difficulties and limitations of data acquisition and random noises.Most of clustering methods can’t be used to deal with incomplete data sets for clustering analysis directly.For this reason,this paper proposes a three-way decision clustering algorithm for incomplete data based on q-nearest neighbors.Firstly,the algorithm finds the q-nearest neighbors for an object with missing values,and the missing value is filled by the average value of q-nearest neighbors. Secondly,it uses the clustering method based on density peaks for the complete data set to obtain the clustering result.For the data object with uncertainty in each cluster,it is designed to the boundary region of a cluster using the three-way decision theory.The three-way decision with interval sets naturally partitions a cluster into three regions as the positive region,boundary region and negative region,which has the advantage of dealing with soft clustering. The experimental results on some UCI data sets and synthetic data sets show preliminarily the effectiveness of the proposed algorithm.

Key words:incomplete data;three-way decision clustering;q-nearest neighbors

*The National Natural Science Foundation of China under Grant Nos.61379114,61272060(国家自然科学基金). Received 2015-06,Accepted 2015-09.