一种基于改进的多值因果图的近似推理

刘绍红，王洪春

(重庆师范大学 数学科学学院，重庆　401331)



一种基于改进的多值因果图的近似推理

刘绍红，王洪春

(重庆师范大学 数学科学学院，重庆401331)

摘要：针对因果图的精确推理是NP难的，提出寻找近似的推理算法。根据以往文献中近似推理的原理，通过一种可能性比值，找到转化后的连接事件概率。该近似推理保证了多值因果图在推理过程中概率的归一性，最后用于实例得出的结果满足概率论知识且符合实际。

关键词：因果图；归一性；近似推理

因果图理论是一种基于概率论的知识表达推理方法，是张勤教授于1994年综合吸收了如故障树、信度网等其他不确定性模型的优点而发展起来的一种不确定性知识的表达和推理模型[1]，常用于故障诊断、预防分析和关系数据的知识处理等领域。采用因果图推理的主要目标是在假定基本事件和连接事件的概率值已知且独立,在证据条件已知下求解指定事件的后验概率[2]。

因果图表现为一种复杂的赋值因果关系网络，网络由节点和有向边构成，每个节点和每条有向边都代表一个事件，每个节点代表一个基本事件或中间事件，每条有向边代表一个连接事件。两个节点之间的连接事件用概率刻画，表示子节点导致父节点发生的概率。如图1中：B1、B2称为基本事件；X3称为节点事件；P13和P23称为连接事件。

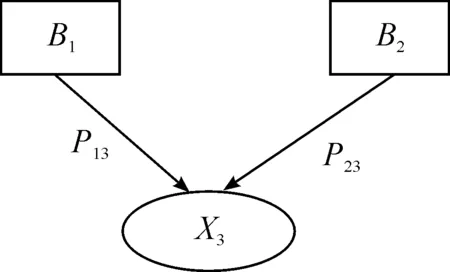
图1　因果图示例

因果图中的假定基本事件和连接事件可能有多种状态(即事件概率是一个矩阵)，到底是哪个状态导致了结果事件的发生，且发生的概率是多大，在实际中是很难确定的。文献[2]提出了单赋值变量和多赋值变量的定义，文献[3-11]提出了一些因果图的近似推理算法，如模糊推理、迭代推理、归一化推理等，但是多值因果图的推理仍是NP难的。于是想到将多值因果图转化为单值因果图，这样就可以用单值因果图的推理方法进行后续计算，但是将单值因果图推理的4步(① 求节点事件的一阶割集CSs-1； ② 求节点事件的最终割集CSs-f；③ 求节点事件的不交化割集DSCs-f；④ 计算某事件的后验概率Pr{Vi|E})直接用于多值因果图中，则存在2个问题：① 不严格满足概率论中的归一性；② 实际中各连接事件不完全具有互斥性。

本文在对多值因果图进行补充定义下，利用事件各状态发生的可能性比值，提出一种多值因果图的近似推理算法。

1补充定义

多值因果图不能直接用单值因果图的推理算法主要是由于某事件各状态发生的概率不一定满足归一性，故要对多值因果图中的基本事件和连接事件进行补充定义。

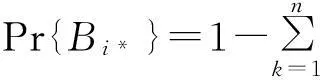
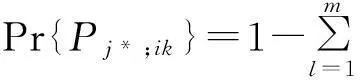
根据补充定义，将多值因果图进行了改进，对变量引入了缺省状态，就不需要对专家给出的数据进行强制归一化处理。

2基本假设

假设1设各基本事件变量Bi相互独立。

假设2设各事件变量(Xi或Bi)各状态发生的概率与其发生的可能性值成正比。

假设3设在多值因果图中原因节点对结果节点只贡献概率值，且每个贡献间是简单相加的关系。

设Vik(k=1,2,…,n)表示Vi的第k状态，Pr{Vik}(k=1,2,…,n)表示Vi的第k状态发生的概率,ψ(Vik)表示事件Vi的第k状态发生的可能性值。事件Vi的各个状态都有一个发生的可能性值，且某个事件的各个状态是互斥的。各状态发生的概率与其发生的可能性值成正比：

若

令

则P(Vik)(k=1,2,…,n)称为状态概率分配因子。

原因事件Vi的第k状态发生时引起结果变量Vj的第l状态发生的概率记为Pjl;ik。

把Vi的所有状态看作一个单事件A,A=Vi1+Vi2+…+Vin,将Vj的所有状态看作一个单事件B，B=Vj1+Vj2+…+Vjm。A引起B的连接事件为P,P发生的概率记为Pr{P}[7]。

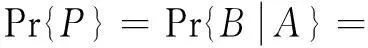
由贝叶斯公式得到

(1)

3实例分析

B4=(B41)∶(0.3)

B5=(B51)∶(0.4)

B6=(B61)∶(0.2)

1) 求一阶割集CSs-1

X1=P41B4∪P21X2

X2=P52B5∪P12X1

X3=P63B6∪P13X1∪P23X2

2) 求最终割集CSs-f

X1=P41B4∪P21P52B5

X2=P52B5∪P12P41B4

X3=P63B6∪P13P41B4∪P13P21P52B5∪

P23P52B5∪P23P12P41B4

最终割集展开成矩阵形式：

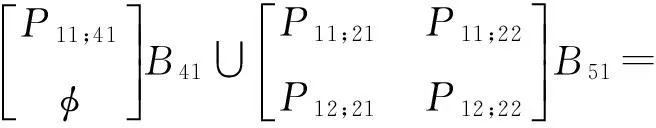
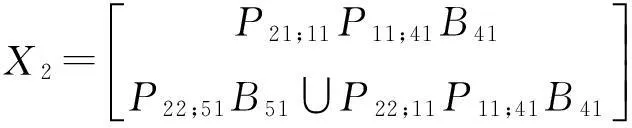
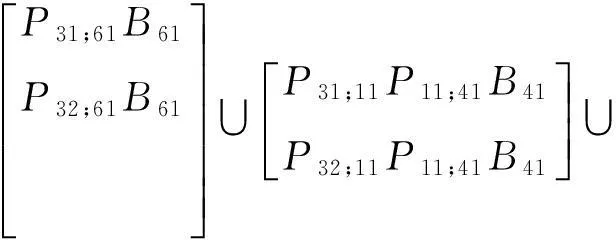
(2)

3) 不交化处理

X11=P11;41B41∪P11;22P22;51B51=P11;41B41+

X12=P12;22P22;51B51=0.32

X21=P21;11P11;41B41=0.21

X22=P22;51B51∪P22;11P11;41B41=P22;51B51∪

本文主要是为了寻求转换后的连接事件概率，所以不需要对X3进行不交化处理。若用经典的因果图推理步骤，应求出每个事件的最终割集和对其进行不交化处理，从式(2)可以看出：对X3进行不交化处理是相当复杂的。这里，可以根据需要对事件最终割集进行不交化处理。

由多值因果图的补充定义有：

ψ(X11)=0.328

ψ(X12)=0.32

ψ(X21)=0.21

ψ(X22)=0.418

从而

(3)

由式(1)得：

Pr{P41}=0.3

Pr{P52}=0.4

Pr{P63}=0.2

Pr{P21}=0.33×(0.7+0.1)+

0.67×(0.1+0.8)=0.867

Pr{P12}=0.51×(0.7+0.1)+

0.49×(0.1+0.8)=0.849

Pr{P23}=0.33×(0.5+0.1)+

0.67×(0.1+0.8)=0.667

Pr{P13}=0.51×(0.6+0.1)+

0.49×(0.1+0.7)=0.749

由式(3)可知基本事件各状态发生概率满足归一性。

图1的多值因果图转化为图3：

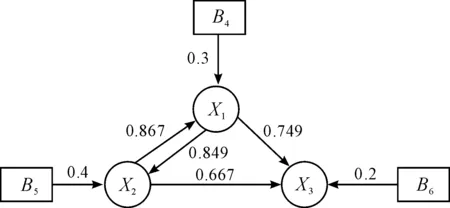
图3　转化后的多值因果图

根据补充定义，各事件的每个状态发生的概率之和为1，满足概率论的归一性，求得转换后的连接事件概率都在(0,1)区间上，说明了转换的合理性。

4结束语

通过多值因果图在补充定义下进行改进，然后向单值因果图转换，可以避开对多值因果图的每个事件都求最终割集和进行不交化处理，也避开了连接事件概率的强制归一。不用求出每个事件的最终割集，从而提高速度，且转换后的连接事件概率是合理、有效的。

参考文献：

[1]ZHANG Q.Probabilistic reasoning based on dynamic causality trees/diagrams[J].Reliability Engineering & Systems Safety，1994,46(94):209-220.

[2]张勤.DUCG:一种新的动态不确定因果知识的表达和推理方法(Ⅰ):离散、静态、证据确定和有向无环图情况[J].计算机学报，2010,33(4):625-651.

[3]樊兴华，张勤，黄席樾.多值因果图的一种推理算法[J].计算机工程与应用,2002,38(3):68-73.

[4]梁新元.复杂因果图并行推理算法研究[J].计算机科学与探索,2014,4:483-493.

[5]王洪春，张勤.基于因果图的一种近似推理算法[J].重庆大学学报(自然科学版),2004,27(8):96-99.

[6]王洪春，石庆喜，张勤.基于因果图的一种推理算法[J].微电子学与计算机,2005,22(5):1-3.

[7]梁新元，吴淑皇，石庆喜.模糊因果图的归一化研究[J].微电子学与计算机，2006,23(11):1-3.

[8]石庆喜，梁新元，张勤.因果图的一种快速推理方法[J].计算机工程与应用,2005,41(28):18-20.

[9]梁新元.因果图迭代推理算法研究[J].系统工程与电子技术,2012,34(6):1299-1304.

[10]樊兴华，仲昕，张勤，等.因果图推理的一种新方法[J].计算机科学,2001,28 (11):48-52.

[11]梁新元.正态模糊因果图的推理算子及归一化算法研究[J].仪器仪表学报，2008,29(2):414-419.

(责任编辑何杰玲)

Approximate Reasoning Based on Improved Multi Valued Causal Graph

LIU Shao-hong, WANG Hong-chun

(School of Mathematical Sciences, Chongqing Normal University, Chongqing 401331, China)

Abstract:The exact inference of causal graph is NP and hard, and the inference algorithm was proposed. Through a possibility ratio, the probability of an event was found after transformation according to the principle of approximate reasoning from previous literature. This approximate reasoning ensured the unification of probability of the multiple value causality diagrams in the reasoning process, and the application to examples drawn from the results meet the knowledge of probability theory and is also in line with the actual.

Key words:causality diagram; normalization; approximate reasoning

文章编号：1674-8425(2016)04-0127-05

中图分类号：TP181

文献标识码：A

doi:10.3969/j.issn.1674-8425(z).2016.04.022

作者简介：刘绍红(1992—)，女，重庆人，硕士研究生，主要从事因果图、人工智能研究。

基金项目：国家社科基金资助项目(13BTJ008)

收稿日期：2015-12-21

引用格式：刘绍红，王洪春.一种基于改进的多值因果图的近似推理[J].重庆理工大学学报(自然科学)，2016(4):127-131.

Citation format：LIU Shao-hong, WANG Hong-chun.Approximate Reasoning Based on Improved Multi Valued Causal Graph[J].Journal of Chongqing University of Technology(Natural Science)，2016(4):127-131.