应用监督局部线性嵌入算法的科技项目质量评价

李　梁，李宗博

(重庆理工大学 计算机科学与工程学院，重庆　400054)



应用监督局部线性嵌入算法的科技项目质量评价

李梁，李宗博

(重庆理工大学 计算机科学与工程学院，重庆400054)

摘要：针对科技项目管理指标的数据维度高且相互影响而呈现出的复杂非线性关系为准确评价和科学管理带来挑战的现状，同时考虑到传统数据降维算法大多对非线性数据映射效果较差，采用监督局部线性嵌入算法，通过数据样本类别信息修改距离公式进行特征维数计算以获得科技项目的真实低维数据。实验结果表明：与传统算法相比，该算法预处理的样本在分类方面具有较高的准确率。

关键词：科技项目；监督；局部线性嵌入；距离公式

近年来，随着经济的快速发展，可为管理部门提供决策信息、实现项目科学管理的科技项目质量评价变得越来越重要。一般来说，科技项目管理指标的特征较复杂，维数较高，呈现出复杂的非线性关系，为信息挖掘带来了困难。处理“维数灾难”[1]是科技项目和其他特征提取工作的首要问题。通过数据降维可以减轻维数灾难和减少高维空间中的其他不相关属性，进而促进高维数据的分类、可视化及压缩[2]。文献[3]未对数据集进行约简，直接使用神经网络对数据进行计算，获得了一定的预测结果，但该处理方法应用范围较小，只针对小样本数据。为了获得更佳的处理效果，必要的特征维数约简成为关键，数据降维在许多领域起着越来越重要的作用。文献[4]采用PCA算法对乔木高光谱遥感数据进行降维处理，获得了效果提升的最佳主成分，避免了高维度容易导致的Hughes现象。文献[5]将核函数引入PCA算法进行改进，使得高维数据降维效果得到改善。文献[6]在解决文档按主题分类问题时，利用线性判别式提取每类的正负特征词进行降维。上述方法基本属于线性降维的范畴，虽然能获得一定效果，但算法复杂度较高，且降维映射过程中会产生较大偏差，无法发现数据间的真实结构。可见，由于受到项目指标特征多且相互影响的限制，传统数据降维方法(尤其是大数据下的降维方法)的运算代价和所需存储空间均受到了挑战。

目前，基于流形的降维方法已成为机器学习、模式识别等领域的研究热点，并成功应用到多个领域[7-9]。本文尝试使用监督局部线性嵌入代替传统局部线性嵌入算法，对样本数据实现目标特征降维，保证样本类别特征在低维映射中的作用，并结合多分类支持向量机分类器进行分类试验。试验结果表明：本文方法的分类正确率有了进一步提高，方法有效，可为相关科技项目质量评价提供参考。

1局部线性嵌入算法

LLE(locally linear embedding)算法[10]是流形学习中使用最广泛的一种算法。LLE的基本思想是：假设样本集分布在高位空间的非线性流形上，但在局部范围内，样本数据具有线性结构的特点，给定任意一个样本均可以利用其自身的近邻样本构成的邻域集合进行线性组合，且这种线性关系在映射降维的过程中保持不变，即低维样本的线性重构系数(权值)和高维样本相同。根据上述思想可以通过求解稀疏矩阵特征向量来获取LLE的低维流形。

给定数据集X={x1,x2,…,xn}，xi∈RD，以欧式距离为基础得到各样本间的距离Dij(i,j∈1,2,…,n)，为每个样本数据xi找到它的k个近邻构成其自身的重构邻域。

利用数据的重构邻域进行重构权值wij的计算，并使得重构函数minε(w)的代价最小

(1)

(2)

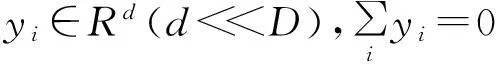
式(2)中：n为样本总数；yi是xi的低维映射表示；y为yi构成的n×d矩阵；w为wij构成的n×n方阵，则在矩阵M中最小的第2至第(d+1)个特征向量值就是所求的低维流形y。

邻域点数k直接定义了流形的最佳分割，若邻域点数k过小，则不能体现各类别的流形特征；若过大，又会增加冗余运算，降低数据的降维性能。k值以及最终低维流形的空间维数d都会对最终降维结果产生影响[11]。

2监督局部线性嵌入

LLE作为一种非监督流形降维算法，未能充分利用已有样本数据的类别属性信息[12]，因此，使用映射后的低维流形提升分类器的性能有待进一步加强。为克服LLE的不足，在传统算法中融入样本类别属性，保持样本间类别信息在低维流形的稳定性是充分挖掘样本数据的有效途径。监督局部线性嵌入(S-LLE)基于同类样本点间距离小于异类样本点间距离的假设，将样本类别计入样本间距离中去，从而修正距离并改进替换传统LLE算法中的欧式距离，使得同类样本点邻域的构成能更准确地体现在低维流形中。

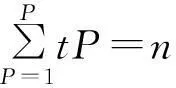
样本距离公式修正为

(3)

其中：Dij为样本xi与xj的欧式距离；Die满足Die=max(Diu),u=1,2,…,n；λ为修正调节程度参数，取值范围为[0,1]；δij为修正参数，用于说明样本点是否属于同类，若样本xi与xj属于同类，则δij=0，否则δij=1。

当λ=0时，算法退化为传统的LLE算法；当λ≠0且逐渐增大时，同类样本间距逐渐小于异类样本间距，使得样本邻域尽可能多地由同类样本构成，达到“类间离散，类内聚合”的效果，最终增强高维映射的精度。使用修正后的距离求解样本数据的邻域，进而结合LLE的后续1、2步骤，即可求出带有样本类别信息的降维后的低维流形数据。

3测试样本降维

测试样本对于衡量分类器性能至关重要。LLE算法对新加入的样本非常敏感，认为这会破坏训练样本原有的拓扑结构，严格来说应对所有测试样本重新求解邻域关系。由于本文测试样本数量少于训练样本，且考虑到算法运行时的效率问题以及算法假设数据自身带有局部线性特征，最后采取线性近似的方法求解测试样本的低维流形数据。大致过程如下：首先，在训练样本邻域的基础上计算测试样本的近邻点；然后，同样以重构函数代价最小为目的计算测试样本的重构权值，并保持该权值不变；最后，依靠训练样本对应的低维流形求出测试样本的低维流形。

4分类实验

4.1实验数据

为了验证算法在评价应用方面的有效性，特地选取某高校科研项目管理平台中的部分数据作为数据集。该数据集包含60个项目样本，其中每个样本的特征有30个。对于空缺值用均值填充，项目评价类别共分为4个等级(优A、良B、一般C、差D)。

4.2实验方法

在分类器选取方面，采用泛化能力较好的支持向量机进行分类[13-14]，提高分类精度。多分类支持向量机在分类时通常有2种方法，即“一对多”法和“一对一”法[15]。由于“一对多”法考虑全局优化致使计算复杂度增大，所以可行性较低。本文使用“一对一”法，将多类问题转化为多个二类问题，建立4×(4-1)/2=6个二类支持向量机，输入测试样本得到各自的类别概率。分类最终结果由较大的概率值决定。

实验分类步骤如下所示：

步骤1数据集按0.8比例随机划分为训练集、测试集。

步骤2对训练集应用S-LLE算法进行降维，保存权值矩阵，并利用该矩阵对测试集进行映射转换，与约减后的训练集特征数目一致。

步骤3将约减训练集输入多分类支持向量机，训练相应参数得到相应模型。

步骤4利用训练模型，针对对应的转换测试集进行测试分类，保存分类结果。

步骤5重复上述1、2、3、4步骤5次，计算分类的平均正确率。

其中：步骤2对数据高维空间降维时，对于式(3)中的调节参数λ设定初始值为0.1，并以步长0.2增加，邻域点数k以训练样本的25%作为最大上限，即k=15，k的下限取10，设定以步长1逐渐增加。低维空间维数d定为特征总数的70%。

利用上述参数对分类实验重复5次，获得使用降维数据分类后的平均正确率，结果如表1所示。

表1　分类后的平均正确率

S-LLE算法受参数λ、k的影响较大，不同的参数组合会产生不同的低维映射，进而影响到分类器性能。由表1的数据可知：随着邻域点数k与调节参数λ逐渐增大，项目分类的正确率会缓慢上升。当组合参数为k=13、λ=0.3时，分类器性能最佳，之后正确率下降，分类器性能受到限制。

4.3降维算法对比实验

为了验证S-LLE算法与传统线性降维算法PCA、非线性降维算法LLE的降维效果，三种算法均相应地对划分后的训练集合进行独立降维，之后结合4.2中实验方法的步骤3～5进行分类。其中，对于S-LLE而言，组合参数选定为k=13、λ=0.3。低维空间维数下限设定为15，并以步长1增加到25。分类实验之前，首先对48个样本分别使用3种算法进行降维，得到二维可视结果，如图1所示。feature1和feature2为降维算法自动选择的2个特征。

利用上述方法实现降维的数据集获取分类特征，从而实现分类。每个实验重复5次，得到不同维数下不同降维算法的分类结果。图2展示了通过各个降维算法处理后的数据集经相同分类器分类后的最终结果。

图1　样本降维结果比较

图2　SVM分类结果

4.4实验结果与分析

由图1可以看出：PCA和LLE对数据的聚合效果较差；S-LLE由于融合了样本类别信息，使得噪声样本在一定程度上得到了抑制，因此聚类效果更加明显。

由图2可知：相应的降维算法均可实现相关数据特征的提取，缩小待处理数据的规模，进而提升分类效果。另外，随着降维特征数目的增加，3条曲线缓慢上升，之后基本保持不变的趋势，总体都在21或22个特征时，SVM的分类准确率达到最优。

传统线性降维算法PCA单纯地以保留样本最大方差为准则实现降维，未充分使用与其他样本间的相关性；LLE与S-LLE算法均为非线性降维算法，在样本间局部线性的前提下进行线性相似表示实现降维，描述出降维后各样本间的真实拓扑结构，保留了更多的价值信息，因而分类准确率高于PCA；S-LLE由于将样本类别融入距离公式进行距离修正，使得同类样本点优先进入邻域进行低维映射计算，最后达到“类间离散，类内聚合”的效果，实现了监督分类，因此分类准确率最高。可见，相比其他算法， S-LLE算法可以提高项目分类的准确率，适合作为科技项目分类问题的预处理算法。

5结束语

由于受到科技项目指标多且数据复杂的影响，对传统LLE降维算法进行了相应改进，并使用处理后的数据进行分类，提升了项目分类的效果。关于如何选取参数组合是今后研究的重点。

参考文献：

[1]毕达天，邱长波，张晗.数据降维技术研究现状及其进展 [J].情报理论与实践，2013，36(2):125-128.

[2]吴晓婷，闫德勤.数据降维方法分析与研究[J].计算机应用研究，2009,26(8):2832-2835.

[3]郑永，陈艳.基于BP神经网络的高校教师教学质量评价模型 [J].重庆理工大学学报(自然科学)，2015，29(1):85-90.

[4]藏卓，林辉，杨敏华.利用PCA算法进行乔木树种高光谱数据降维与分类[J].测绘科学，2014,39(2):146-149.

[5]王瀛，郭雷，梁楠.基于优选样本的KPCA高光谱图像降维方法[J].光子学报，2011，40(6)：847-851.

[6]徐敏，张丽萍，朱梧槚.基于Fisher线性判别式的层次文档分类[J].南京理工大学学报(自然科学版)，2005，29(4)：460-463.

[7]向丹，葛爽.基于EMD样本熵和流形学习的故障特征提取方法 [J].航空动力学报，2014,29(7):1533-1540.

[8]倪志伟，薛永坚，倪丽萍，等.基于流形学习的多核SVM财务预警方法研究 [J].系统工程理论与实践，2014，34(10)：2666-2674.

[9]汤宝平，马婧华.多准则融合敏感特征选择和自适应邻域的流形学习故障诊断[J].仪器仪表学报，2014，35(11)：2413-2420.

[10]ROWELS S T,SAUL L K.Nonlinear dimensionality reduction by locally linear embedding [J].Science,2000,290(5500):2323-2326.

[11]文贵华，包丽，丁月华.局部线性嵌入算法中参数的选取 [J].计算机应用研究，2007,43(9):179-183.

[12]董安，潘宏侠，龚明.基于局部线性嵌入算法的柴油机故障诊断研究 [J].计算机工程与应用，2013,49(22):236-240.

[13]GENTLE J E，HARDLE W K，MORI Y C.Handbook of Computational Statistics:Concepts and Methods[M]． Second Edition:Springer Press，2012:883-926.

[14]李利杰，张君华，熊伟清，等.一种改进的支持向量机模型优化算法 [J].计算机技术与发展，2014(12):22-26.

[15]韩兆洲，林少萍，郑博儒.多类支持向量机分类技术及实证 [J].统计与决策，2015(19):10-13.

(责任编辑杨黎丽)

Evaluation of the Quality of Technology Projects Based on Supervised Locally Linear Embedded Algorithm

LI Liang, LI Zong-bo

(College of Computer Science and Engineering,Chongqing University of Technology, Chongqing 400054, China)

Abstract:Dimension of indicators data about technology project is the higher, and has interaction influence, and shows complex nonlinear relationship, which brings challenges for the accurate evaluation of scientific management. Considering that most of traditional reduction algorithms about data dimension are poor for nonlinear effects of mapping data, so that we used supervised locally linear embedding algorithm to modify the distance formula according to data sample classification information, finally we calculated the feature and got the real low-dimensional data. The experimental results show that compared with the traditional algorithm, the sample data preprocessed algorithm has a higher accuracy on the performance of classification.

Key words:technology project; supervision; locally linear embedding; distance formula

文章编号：1674-8425(2016)04-0097-05

中图分类号：TP301

文献标识码：A

doi:10.3969/j.issn.1674-8425(z).2016.04.017

作者简介：李梁(1964—)，男，重庆人，副教授，主要从事数据挖掘和数据仓库、数据库技术研究；李宗博(1986—)，男，河北沧州人，硕士研究生，主要从事数据管理技术研究。

基金项目：重庆市应用开发计划项目(CSTC2013yykfA40002)

收稿日期：2015-11-28

引用格式：李梁，李宗博.应用监督局部线性嵌入算法的科技项目质量评价[J].重庆理工大学学报(自然科学)，2016(4):97-101.

Citation format：LI Liang, LI Zong-bo.Evaluation of the Quality of Technology Projects Based on Supervised Locally Linear Embedded Algorithm[J].Journal of Chongqing University of Technology(Natural Science)，2016(4):97-101.