脑出血中豆纹动脉出血易发点的流固耦合分析

许长兴，张　华，胡文超

(重庆大学 航空航天学院，重庆　400044)



脑出血中豆纹动脉出血易发点的流固耦合分析

许长兴，张华，胡文超

(重庆大学 航空航天学院，重庆400044)

摘要：建立了大脑中动脉M1段与豆纹动脉(LSA)管壁/血液耦合模型。采用有限元法，利用ANSYS WORKBENCH中Transient Structural 和CFX 相互结合的专用流固耦合算法Fluid Solid Interface 实现结构分析和流体分析的双向耦合计算，其中假设血管壁为各项同性线弹性体，血液为不可压缩牛顿流体，用有限元方法对大脑中动脉段M1段与豆纹动脉血管内的血流情况进行了数值模拟，在给定进出口血压条件下模拟出豆纹动脉弹性管壁压强、应力、应变分布与血液流场分布，并由此构建了豆纹动脉近似等强度模型。临床显示颅内压增高与血压增高可导致脑部丘脑部位供血不足，即豆纹动脉末端流速减慢。在近似等强度模型下，通过对比分析发现：随着豆纹动脉末端流速的减慢，豆纹动脉内血压增高，且距离末端越近，血压增高幅度越大，导致末段附近等效应力大幅度提高，形成管壁破裂易发点，即为豆纹动脉出血危险部位,与临床统计的脑动脉出血高发部位相吻合。

关键词：豆纹动脉；血管模型；有限元分析；流固耦合；等效应力

在中国，脑卒中是仅次于肿瘤和心脏病的第三大致死性疾病(卫生部《2011中国卫生统计年鉴》)。脑卒中包括缺血性脑卒中和出血性脑卒中，其中脑出血防治仍未取得明显的进展，成为脑血管病中致残和致死率最高的疾病。目前，中国高血压脑出血年发病人数为200万，累计每年约150万人死于脑出血[1]。近年来国际上已开始重视对脑出血的研究，投入了巨大的人力和物力，脑出血的发病率和死亡率开始下降。而中国在脑出血领域的研究却相对滞后，研究的投入和支持力度有待加强。结合我国高血压脑出血的发病特点和规律，深入探索其发生、发展机制，寻找有效预警标志与防治新策略，降低发生率和死残率，对保障国民身体健康具有重大意义。

高血压脑出血高发部位在豆纹动脉供血的丘脑基底节区，具有独特的解剖生理特点：① 独特的血流动力学特点。豆纹动脉从大脑中动脉以直角发出供应基底节、尾状核和内囊区，豆纹动脉易破裂节段承受了上级分支与下级分支之间约有6.7 kPa 的脉压差[2-3]。② 特殊的力学边界条件。高血压脑出血的责任血管以直径为150～660 μm的小动脉为主[4]，该区域血管周围主要由疏松的白质纤维束构成，靠近脑室，血管内外压力差明显，具备血管易破的力学边界条件。因此，明确豆纹动脉出血易发部位的结构特征、流场特征、血管力学特性和受力特征，为豆纹动脉出血预警提供参照依据是十分必要的。

近年来，流固耦合分析研究和应用取得了飞速的发展，在生物力学(如血液的流动)、新型工程材料(如磁流变液)特性的研究[5]等方面得到了广泛应用。

1豆纹动脉

动脉起自心脏，从心脏发出后不断分支，最后发展为毛细血管，其管径随分支逐渐减小。在不断分支与远离心脏的过程中，动脉血压逐渐降低，血液流速相对变缓，管壁随着血压的降低与血流作用的减弱逐渐变薄。在人体的生长进化过程中血管最终成为等强度模型，符合自然界不断进化的变化规律。由于豆纹动脉过于细小，只能测量出其管径大小而无法通过检测手段得知其管臂厚度及变化，所以通过有限元模拟建立一种在人体正常生理状态下的一种血管近似等强度模型是十分必要的。该模型的确定为模拟豆纹动脉在颅内压增高、不同等级的高血压等病理状态下的血流、管壁应力、应变分析以及出血易发点预测提供了分析基础。

豆纹动脉起自打包中动脉M1段，是供应纹状体和内囊的主要动脉，易破裂出血，故又名“出血动脉”。胡福广等[6]测得大脑中动脉的 M1 段长度为 18.58±4.51 mm，外径约为3.6 mm，豆纹动脉外径约为5 mm。人体生长发育过程中血管分支有两种方式：绝大部分血管分支是以与主干偏折较小角度的方式来发出分支血管，其目的是避免血液流向改变过大造成对管壁的冲击损伤；另一种分支方式遵循的原则为最短路径原则[7]。大脑中动脉分支的方式即遵循最短路径原则，也就导致了较多的大脑血管相关性疾病的发生[8]。大脑中动脉发出的豆纹动脉多以直角或近似直角的方式发出[9]，豆纹动脉几乎存在于所有的大脑半球，主要起自 M1 段外侧部，形成“S”形弯曲后进入前穿质。这种曲折的行程可尽可能减缓血液的流速，起到调节血压的作用[10]。

在生理学上血液为非牛顿流体，血管壁为黏弹性体，在血液与管壁的流固耦合中所有的研究者都做了不同程度的简化假设,引入了各种计算模型。基本的简化假设有两个：其一，将血管壁看做刚性或线弹性管壁；其二,把血液看成牛顿流体。Aenis等[11]的研究结果表明：采用牛顿流体与非牛顿流体模型时,流场的差别不大。体外模拟实验也得出相同结果[12]。本文主要分析豆纹动脉破裂危险部位，即出血易发点，更侧重于血管壁部分的受力变形，所以本文血液采用不可压缩牛顿流体模型，而血管壁采用线弹性体，相对于刚性管壁更接近人体真实环境。

2脑动脉的流固耦合动力学模型

1) 血流动力学方程

假定血液是层流且黏性的、不可压缩的牛顿流体[13-14]。控制流动的基本方程是不可压缩Navier-Stokes方程。

(1)

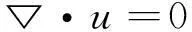
(2)

式中um是流体网格速度。

(3)

(4)

(5)

初始条件：速度压力均为0。其中：ρ为密度，数值为1 050 kg/m3；P为压强；u为速度；μ为运动黏度系数，数值为0.003 5 Pa/s。

2) 血管壁的动力学方程

壁面条件设定：假定血管为不可压缩的各项同性材料[15-17],密度ρ=1.06×103kg/m3，弹性模量E=2.7 MPa，泊松比为0.45(接近不可压缩材料)

3) 流固耦合面条件

① 无滑移；

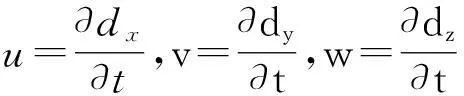
③ df=ds；

④ σf·nf=σs·ns；

d,σ,n分别标示位移、应力张量、边界法向；下标f,s分别代表流体和固体。

3模型建立、划分网格与边界条件

本文所建模型为M1段直径为3.6mm、长度为20mm的血管。豆纹动脉从距离M1段起始部位为10mm的位置以直角形式发出，发出后豆纹动脉在近端有“s”型走向，长度约25mm。本模型豆纹动脉部分血管内径依照血液横截面积保持不变为原则，内径为 0.4mm，分支后内径为为0.283mm，起始部位外径5mm，随距离起始部位长度变大而逐渐减小，保证豆纹动脉血管为近似等强度血管。血管三维模型如图1所示。该模型豆纹动脉形态尺寸与人体实际构造近似，且本文所建立模型为近似等强度模型，使豆纹动脉在正常血压状态下各部位等效应力近似相等。与实际情况的主要差别在于，本模型只有一根豆纹动脉从大脑动脉分支出来，而实际豆纹动脉为多支。本文主要分析豆纹动脉的出血易发点，所以对模型进行简化，只进行单根豆纹动脉的流固耦合分析。

在FSI(fluid solid interface)流固耦合分析技术中，固液的网格划分采取不同的方式来进行。管壁运用Ansys Workbench里的Meshing来进行扫掠划分，并在分支处做局部细化，共有287 083个节点，145 446个单元，如图2所示。流体采用ICEM CFD来划分并在细节部位提高精度，共 72 375 个节点、348 937个单元，如图3所示。在初始条件中设定壁面无滑移。在边界条件中，由于豆纹动脉易破裂节段承受了上级分支与下级分支之间约6.7 kPa的脉压差[2-3]，所以假设进出口管壁面的自由度为0，大脑中动脉出口压力为10 kPa，进口处压力为10.5 kPa，豆纹动脉出口处压力设为4 kPa。

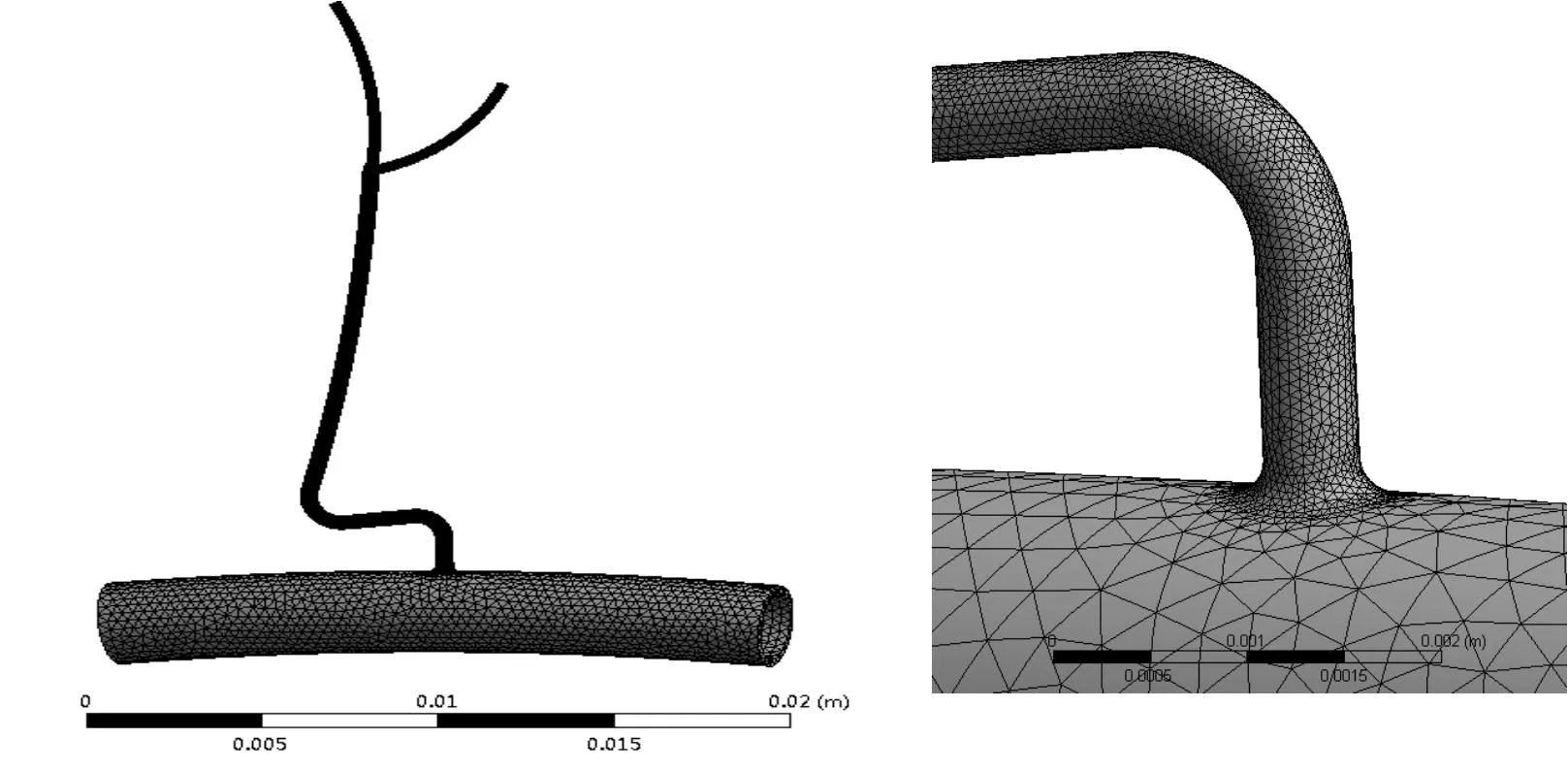
图2　血管网格划分

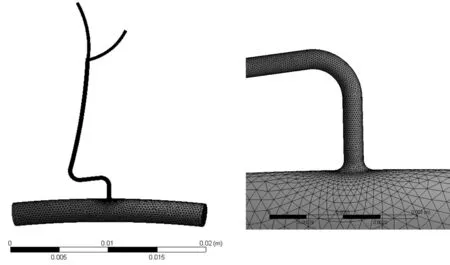
图3　血液网格划分

4计算结果与分析

4.1模型尺寸确定与参考点设定

本文在Transient Structrual和CFX两个模块的基础上，通过专用的流固耦合算法实现结构分析和流体分析的双向耦合计算，在Transient Structrual和CFX中设置相同的耦合时间和耦合时间步，分别为1 s和0.1 s，以实现流场与结构上的耦合计算。

计算结果在CFX-Post中显现。为了直观地分析，本文在豆纹动脉内壁上选取6个参考点测量其等效应力值，参考点位置如图4所示。通过对模拟结果的分析发现：大脑中动脉中的流速在0.85～0.90 m/s，比较符合正常人大脑中动脉流速，此时豆纹动脉出口处速度约为1.25 m/s。流场如图5所示，此时通过不断调整豆纹动脉外径使得豆纹动脉血管内壁各处等效应力在42～45 kPa 之间，等效应力近似相等，使其基本符合设计要求的等强度模型。在模型中豆纹动脉起始端外径为0.5 mm，分叉前外径为0.45 mm，分叉后外径为0.318 mm，豆纹动脉末端外径为0.31 mm。等效应力如图6所示。

图4　参考点设置

图5　血液流场

图6　等效应力

4.2出血易发点结果分析

颅内压简称ICP，颅内压增高会导致脑供血不足。Barcroft[18]在1943 年研究发现：ICP增高至一定值时脑血流量开始有明显下降。Mcintosh[19]在动物实验中发现：当动物颅内压增高后，动物大脑皮质平均局部脑血流量降低。同样临床医学研究结果表明：高血压会引起脑血管痉挛以及血管调节功能减退,导致严重的脑血流量降低,出现不同程度的脑动脉供血不足症状。上述颅内压与血压的升高，都导致丘脑和基底节区供血的豆纹动脉流速降低，所以在本文模拟过程中，将模型中豆纹动脉末端的血液流速逐渐降低，分析其流场与管壁的受力变化，找到此状态下可能导致豆纹动脉出血的危险点，为临床医学提供参考。

当人体血压增高、大脑颅内压增高时，豆纹动脉末端血液流速减慢，对应此种人体状态，有限元模拟将边界条件的豆纹动脉出口压强4 kPa改为速度条件，速度线性变化从1.25 m/s降至0.25 m/s，如图7所示。在此边界条件下6个参考点的等效应力值随豆纹动脉末端出口速度的变化如图8所示，从中可以看出：参考点1,2在末端附近，等效应力值明显增加，达到90 kPa以上；而其余4个参考点幅值变化不大，且越接近大脑中动脉变化幅值越小。由此结果可以看出：随着大脑颅内压与血压的增高，豆纹动脉末端血液流速降低，豆纹动脉远端等效应力值显著增加，相对于其他部位，更易导致血管破裂出血，形成豆纹动脉出血易发点。

当豆纹动脉末端血液流速分别为v=1.25 m/s(左)和v=0.25 m/s(右)时，6个参考点附近局部等效应力如图9所示，从中对比可以看出：参考点1与参考点2附近的等效应力明显增大，由45 kPa增加至90 kPa以上，约为原来的2倍；而参考点3附近的等效应力增加至65 kPa左右，有一定幅度的提高；参考点4附近增加至60 kPa左右；参考点5、6两点等效应力变为50 kPa左右，变化幅度较小。参考点1附近随豆纹动脉末端血液流速减慢对应的局部等效应力如图10所示。从图9、10可以发现：随豆纹动脉末端流速的减慢，豆纹动脉等效应力升高，且距离末端越近，增高幅度越大。

图8　各参考点等效应力值随末端速度变化的曲线

图9　豆纹动脉末端血液流速分别为v=1.25 m/s(左)，v=0.25 m/s(右)时6个参考点附近局部等效应力

图10　参考点1附近随豆纹动脉末端流速血液减慢

5讨论

目前大多数血管生物力学主要针对冠状动脉、颈动脉与动脉瘤的血管血流分析，针对豆纹动脉的生物力学分析相对较少。大多数生物力学主要单独分析血管壁的力学属性或人体血液流动情况，而对血流-血管耦联的流固耦合的有限元分析相对较少。本文血管采用弹性材料，用有限元方法对豆纹动脉血管内的血流情况进行了数值模拟，在给定正常生理血压条件下模拟出豆纹动脉弹性管壁应力、应变分布与血液流场分布，为临床医学提供参考。

本文模拟结果显示：当人体颅内压增高、血压增高导致豆纹动脉末端血液流速减慢时，豆纹动脉内等效应力增高，且距离末端越近，应力增高幅度越大，形成管壁破裂易发点，即豆纹动脉出血危险部位；豆纹动脉出血易发点位于豆纹动脉远端。根据国际疾病分类(International Classification of Diseases-10,ICD-10) 的分级方法[20]，将患者的出血部位分成深部(基底核区和丘脑)、脑叶(单个或多脑叶)、脑干、小脑、脑室(排除脑实质出血破入脑室)、多个部位(同时存在2个部位的出血)。Wang和Ruiz-Sandoval等[21-22]的临床调查研究结果表明：在脑出血的各出血部位中，以深部(基底核区、丘脑)出血居多，超过总量的60%。本文的模拟结果显示：豆纹动脉出血易发点位于豆纹动脉远端，即豆纹动脉供血的丘脑、基底节区，与临床调查结果相符。

脑卒中问题现主要处在医疗治疗方面，针对其发生机理与预防的研究相对较少。本文主要从出血性脑卒中的发病机制出发，通过力学手段分析人体的医学问题，通过CAD软件对人体大脑血管进行三维建模，建立大脑中动脉与豆纹动脉模型，通过血流血管流固耦合的有限元分析研究大脑中动脉与豆纹动脉的血液流动情况和血管壁的应力应变状况，得出高血压脑出血高发部位位于基底节区,从而为临床医学提供力学参数参考。

参考文献：

[1]FEIGIN V L,LAWES C M,BENNETT D A,et al. Worldwide stroke incidence and early case fatality reported in 56 population-based studies:a systematic review[J].Lancet Neurol,2009,8(4):355-369.

[2]RHODIN J A.The ultrastructure of mammalian arterioles and precapillary sphincters[J].J Ultrastruct Res,1967,18(1):181-223.

[3]WIEDERHIELM C A,WOODBURY J W,KIRK S,et al. Pulsatile Pressures in the Microcirculation of Frog’s Mesentery[J].Am J Physiol,1964,207:173-176.

[4]TAKAKEBAYASHI S,KANEKO M.Electron microscopic studies of ruptured arteries in hypertensive intracerebral hemorrhage[J].Stroke,1983,14(1):28-36.

[5]CHEN S,HUANG J,SHU H Y,et al.Analysis and Testing of Chain Characteristics and Rheological Properties for Magnetorheological Fluid[J].Advances in Materials Science and Engineering,2013,29:691.

[6]胡福广,张皓峰,岳立峰.脑外侧裂区显微外科解剖学研究[J].中国神经精神疾病杂志,2010(5):272-275.

[7]秦建军,边进才,刘俊文，等.大脑中动脉的显微解剖[J].河北职工医学院学报,1995(4):36-41.

[8]毛增荣,张鋆.脑底诸动脉及其分枝[J].解剖学报， 1958(2):37-56.

[9]王克臻,李岩,马威,等.正常成人脑动脉的 MRA 测量和应用解剖研究[J].中国临床解剖学杂志,2008(4):392-395.

[10]韩 卉,张为龙.人大脑中动脉中央支脑内段的研究[J].解剖学报，1993,24(1):12-16.

[11]AENIS M,STANCAMPIANO A P.Modeling of flow in a straight stented and nonstented side wall aneurysm model[J].Journal of Biomechanical Engineering,1997,119(2):206-212.

[12]ERNEMANN U U,GRONEWALLER E,et al.Influence of geometric and hemodynamic parameters on aneurysm visualization during three-dimensional rotational angiography:An in vitro study[J].AMERICAN JOURNAL OF NEURORADIOLOGY,2003,24(4):597-603.

[13]MILNER J S,MOORE J A,RUTT B K,et al.Hemodynamics of human carotid artery bifurcations:computational studies with models reconstructed from magnetic resonance imaging of normal subjects[J].Journal of vascular surgery,1998,28(1):143-156.

[14]WOOD N B,WESTON S J.KILNER P J,et al.Combined MR imaging and CFD Simulation of flow in the human descending aorta[J].Journal of Magnetic Resonance Imaging,2001,13(5):699-713.

[15]Di MARTINO E S,GUADAGNI G,FUMERO A,et al.Fluid-structure interaction within realistic three-dimensional models of the aneurysmatic aorta as a guidance to assess the risk of rupture of the aneurysm[J].Med Eng Phys,2001,23(9):647-655.

[16]GAO F,GUO Z H,SAKAMOTO M,et al.Fluid-structure Interaction within a Layered Aortic Arch Model[J].Journal of Biological Physics,2006,32(5):435-454.

[17]KELLY S,O’ROURKE M.Fluid,solid and fluid-structure interaction simulations on patient-based abdominal aortic aneurysm models[J].Proc Inst Mech Eng H,2012,226(4):288-304.

[18]BARCROFT H,EDHOLM O G.The effect of temperature on blood flow and deep temperature in the human forearm[J].J Physiol,1943,10(2):5-20.

[19]MCINTOSH T K,NOBEL L,ANDEREW B,et al.Traumatic brain injury in the rat:characterization of a midline fluid-percussion model[J].Cent Nerv Syst Trauma,1987,4:119-134.

[20]Van DRIMMELEN-KRABBE J J,BRADLEY W G,ORGOGOZO J M,et al.The application of the international statistical classification of diseases to neurology:ICD-10 Na[J].J Neurol Sci,1998,161(1):2-9.

[21]WANG W J,LU J J,WANG Y J,et al.Clinical Characteristics,Management,and Functional Outcomes in Chinese Patients Within the First Year After Intracerebral Hemorrhage:Analysis from China National Stroke Registry[J].CNS Neurosci Ther,2012,18(9):773-780.

[22]RUIZ-SANDOVAL J L,CHIQUETE E,GARATE-CARRILLO A,et al.Spontaneous intracerebral hemorrhage in Mexico:results from a Multicenter Nationwide Hospital-based Registry on Cerebrovascular Disease (RENAMEVASC)[J].Rev Neurol,2011,53(12):705-712.

(责任编辑何杰玲)

Fluid-Solid Interactive Analysis of Bleeding-Prone Points of LSA in Cerebral Hemorrhage

XU Chang-xing, ZHANG Hua, HU Wen-chao

(College of Aerospace Engineering, Chongqing University, Chongqing 400044, China)

Abstract:The wall-blood interactive model of M1 segment of the middle cerebral artery and the lenticulostriate artery (LSA) of brain was established, and then two-way interactive calculation of structural analysis and fluid analysis were achieved by finite element method (FEM) and the special Fluid-Solid interactive algorithm which combinesd Transient Structural and CFX. In experiment, the vascular wall was assumed as the isotropic linear and elastomeric, and the blood was incompressible Newtonian fluid. The numerical simulation was carried out in terms of the blood flow of M1 segment of the middle cerebral artery segment and the LSA by FEM. Under the given conditions of entrance and outlet of vessels’ blood pressure, we simulated the pressure, stresses, strains distribution and flow field distribution and built lenticulostriate artery approximately equal strength model. Under the model, the results of experiment and simulation show that the blood pressure within the LSA increases when the flowing velocity of the LSA is slow. Especially, the magnitude of the blood pressure is greater when it close the end. It leads to the substantial increasing of the equivalent stress near the end, and forms the rupture-prone points of the wall which are dangerous parts of the LSA bleeding. These results of experiment and simulation have a high match with the clinical statistics on the cerebral arterial bleeding site.

Key words:lenticulostriate artery; vessel model; finite element analysis; fluid-solid interaction; equivalent stress

文章编号：1674-8425(2016)04-0066-07

中图分类号：R54

文献标识码：A

doi:10.3969/j.issn.1674-8425(z).2016.04.012

作者简介：许长兴(1991—)，男，硕士，主要从事流固耦合分析和结构优化设计研究。

基金项目：国家重点基础研究计划(973计划)资助项目“出血性脑卒中发生发展机制及其防治的基础研究”(2014CB541600)

收稿日期：2016-01-21

引用格式：许长兴，张华，胡文超.脑出血中豆纹动脉出血易发点的流固耦合分析[J].重庆理工大学学报(自然科学)，2016(4):66-72.

Citation format：XU Chang-xing, ZHANG Hua, HU Wen-chao.Fluid-Solid Interactive Analysis of Bleeding-Prone Points of LSA in Cerebral Hemorrhage[J].Journal of Chongqing University of Technology(Natural Science)，2016(4):66-72.