工程测量中引入复数计算坐标转换研究分析

杨伟星

(中国电建集团西北勘测设计研究院有限公司，西安　710065)



工程测量中引入复数计算坐标转换研究分析

杨伟星

(中国电建集团西北勘测设计研究院有限公司，西安710065)

摘要：通过引入复数的模、复角、旋转角和尺度参数，对工程中大地坐标与施工坐标之间相互转化进行分析、研究、合理优化，从而得出了适合工程应用的简洁公式，避免了测量施工中施工坐标和大地坐标之间因转换带来的不便，从而提高了工作效率。同时，文章通过对多种计算方法的比较分析和相关数据的验证，为测量人员提供参考。

关键词：复数;尺度参数；施工坐标;大地坐标

0前言

为了施工方便，根据工程需要，在工程施工过程中往往要将施工坐标转化成施工小坐标，尤其是在隧洞防线中应用极为广泛。传统的平面坐标转换公式过于繁琐，不便于CASIO编程计算器编程，条件判断多、公式复杂、平移量和旋转角度求解麻烦。鉴于以上弊端，本文引进复数概念，借助复数的复角、模、缩放尺度、平移参数，对大地坐标和施工坐标之间相互转换进行全新推导[1-3]，从而，找出更适合工程实际与能方便编程应用的公式，大大提高工作效率。

1测量高斯平面直角坐标系下坐标转换公式推导

由图1可知，在测量高斯平面直角坐标系下坐标相互转化之间关系，原坐标系xoy，P点坐标(xP,yP)，通过坐标平移和旋转得到新坐标系下P点坐标(xP′,yP′)，坐标原O平移到O′，原坐标系下O在新坐标系x′oy′下O′坐标(xo′,yo′)[4]。其中xo′,yo′为坐标平移量，θ为原坐标新变换到新坐标系下的旋转角度，在测量中通常用方位角来表示[4]。根据图1的几个关系可知：

(1)

(2)

将式(2)带入式(1)中得：

(3)

(4)

式(3)、(4)为在测量高斯平面直角坐标系下的原坐标系转化到新坐标系下的公式。

由式(3)得：

(5)

将式(5)带入式(4)得：

(6)

将式(6)带入式(4)得：

(7)

式(6)和式(7)是在测量高斯平面直角坐标系新坐标系下坐标转化到原坐标系的转化公式[5-6]。

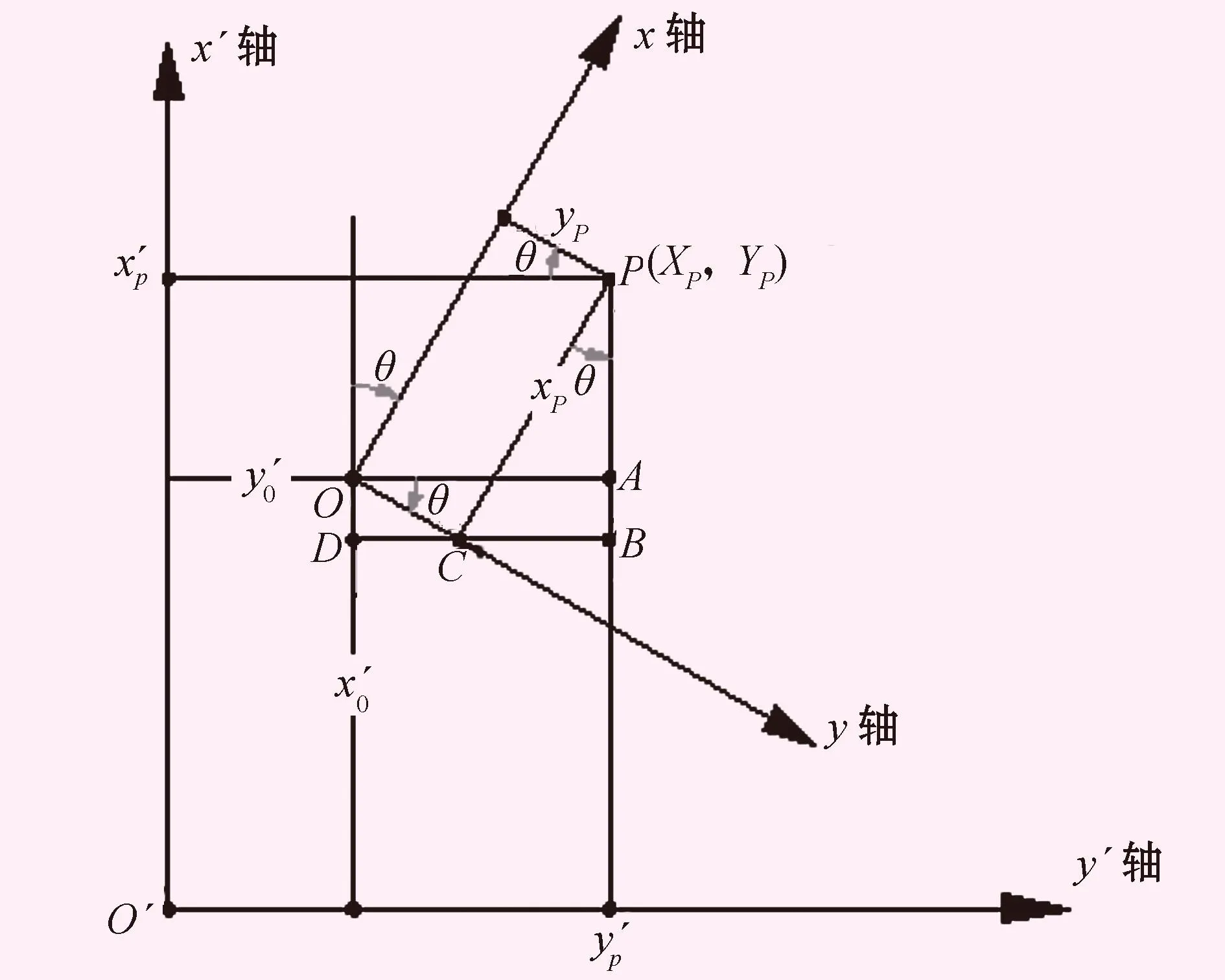
图1　测量高斯平面直角坐标系图

2测量高斯平面直角坐标系复平面下坐标转换公式推导

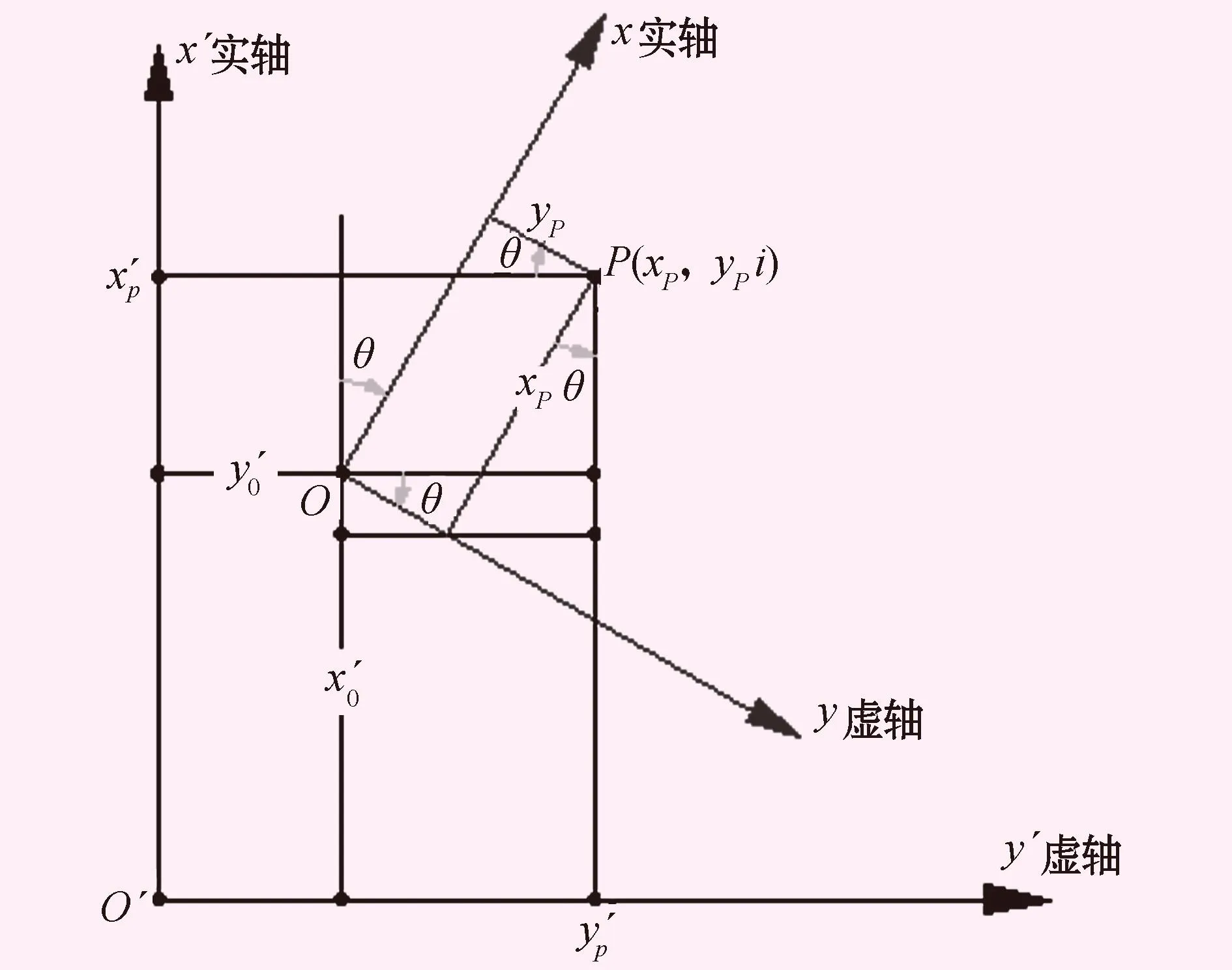
图2　测量高斯平面直角坐标系复平面图

由图2可知，测量高斯平面直角坐标系复平面下坐标转换之间相互关系。原系复平面下点P复数坐标形式(xP,yPi)，新系复平面下P′复数形式(xP′,yP′i)，原系原点O在新系下复数形式(xo′,yo′i)。根据高斯平面坐标系线性变换几何意义：有原系下坐标变换到新系下坐标，将原系下坐标旋转θ角度，加入缩放尺度参数κ，加平移参数(xo′,yo′)后即可变为新系下坐标，反之亦然[1,4]。

由复数的性质可知：2个复数的乘积的模等于他们的模的乘积，2个复数乘积的复角等于它们的复角和。因此，假设2个复数z1、z2

(8)

(9)

则有：

(10)

在高斯复平面系下，坐标平移参数的复数形式为zo′=xo′+yo′i，旋转角θ为复数的模，缩放尺度参数κ为复数的模，根据复数的性质可知，旋转尺度的复数形式为zθ=κ∠θ。

由图2可知，公共点P在原系和新系下的复数形式分别为：zP=xP+yPi和zP′=xP′+yP′i。

根据复数的几何意义和2个复数乘积的性质可知，将原系下坐标复平面上的点zP乘以旋转尺度zθ，再加上平移复数zo′，等于该新系下坐标复平面zP′的复数形式，故有以下方程式。

(11)

设坐标点P1、P2在原坐标系xoy复平面下复数形式分别为z1=x1+y1i和z2=x2+y2i，在新系x′o′y′复平面下复数形式分别为z1′=x1′+y1′i和z2′=x2′+y2′i。则由公式(11)可得：

(12)

(13)

将式(12)减式(13)可得旋转尺度复数形式为：

(14)

将(14)带入(12)或(13)中的平移复数形式为：

(15)

由式(11)可得坐标转换反算公式：

(16)

公式(11)、(14)、(15)、(16)即为高斯平面直角坐标复平面下坐标相互转换公式。

3测量高斯平面直角坐标系下与复平面系下数据比较分析

为了验证上面2种坐标系下坐标转换公式的正确和实用性，选在了某电站坝轴线及两侧的点进行大地坐标和施工坐标之间转换数据进行采集分析。在测量高斯平面直角坐标系下，公式(7)和(6)为大地坐标转换为施工坐标公式，公式(3)和(4)为施工坐标转化为大地坐标公式。在测量高斯平面直角坐标系复平面下，公式(11)、(14)和(15)为大地坐标转化为施工坐标公式，公式(14)、(15)和(16)为测量坐标转化为大地坐标公式。通过下面的数据进行分析验证。

3.1测量高斯平面直角坐标系下坐标转换实例分析

已知大坝轴线两端点B1、B2，将其转换成施工坐标，要求其以B1、B2为轴线 进行相应坐标转换。转化数据如表1。

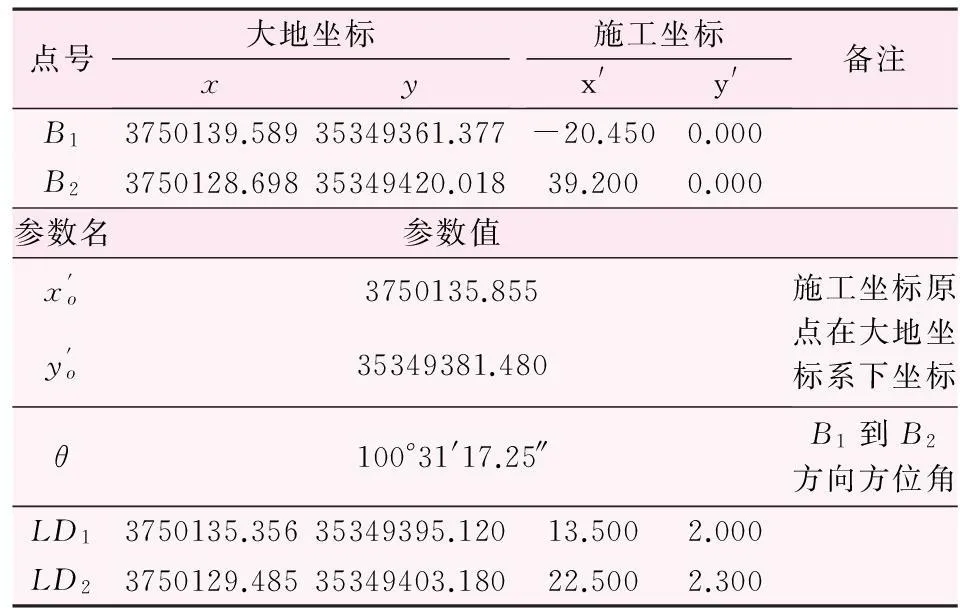
表1　　　测量高斯坐标平面直角坐标系下大地坐标与施工

由表1转换数据可以看出，在工程测量中只要知道了坐标转换参数xo′、yo′、θ就可以进行坐标转换。在测量高斯直角平面坐标系下，转换参数可以用坐标正反算进行求解。

3.2测量高斯平面直角坐标复平面系下坐标转换实例分析

已知大坝轴线两端点B1、B2，将其转换成施工坐标，要求其以B1、B2为轴线 进行相应坐标转换。转化数据如表2。

由表2知，运用复数进行大地坐标与施工坐标系之间相互转换时，需要确定4个转换参数xo′、yo′、κ、θ，这4个转换参数可以用复数运算进行求解。

3.32种坐标系下大地坐标与施工坐标相互转换比较分析

由表1,2可以看出，不管用那种方法进行大地坐标与施工坐标相互转换，其转换结果一样。测量高斯平面直角坐标系下需要求解3个参数，参数求解要有一定的限制，先要找好轴线，再用坐标正反算求之。测量高斯平面直角坐标复平面系下则只要知道两点就可以求解出相应的参数。在复平面里多了个缩放比例κ，κ值的精度决定了所求坐标的精度，当κ为1没有缩放，则测量高斯平面直角坐标系下的坐标转换是测量高斯平面直角坐标复平面系下坐标转换的特例。

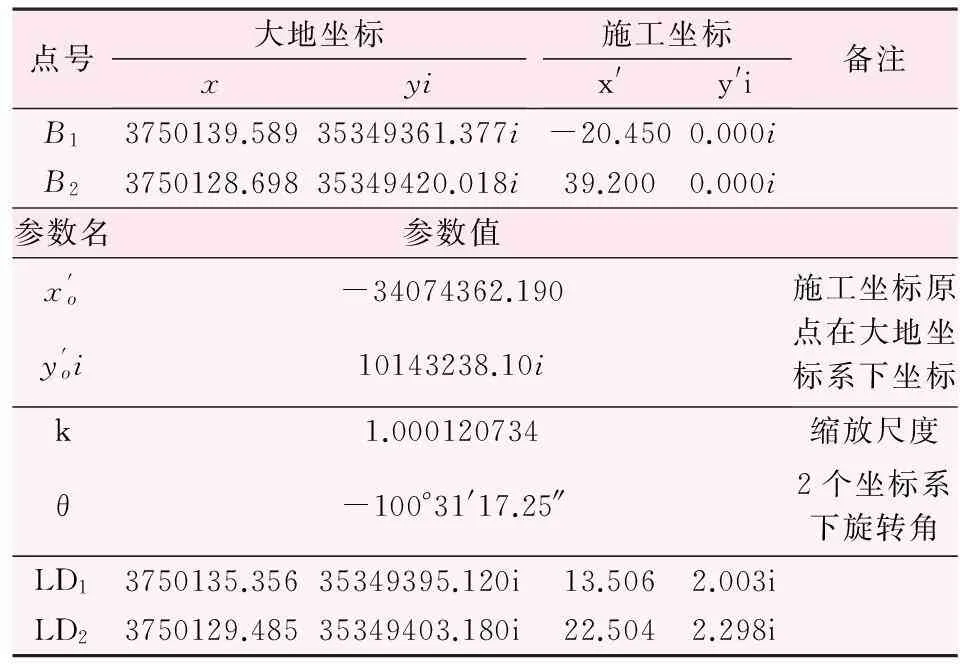
表2　　　测量高斯坐标平面直角坐标复平面系下大地坐标与

4结语

通过在施工测量中引入复数求解坐标转换：

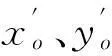
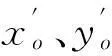
(3) 引入复数后使得坐标转换更加简单化，在复数计算中缩放尺度的引入可以使公式变得更加完整。

参考文献:

[1]覃辉.CASIOfx-5800P编程计算器公路与铁路施工测量程序转换[M].上海：同济大学出版社,2009.

[2]孔祥元,郭际明,刘宗全.大地测量学基础[M].武汉：武汉大学出版社,2001.

[3]覃辉.《测量学》教材内容的改革与探索[J].测绘科学,2008(6)：229-232.

[4]杨伟星.复数在坐标正反算计算中的应用[J].西北水电,2015(3):15-17.

[5]杨伟星,张建生,张堃.引水隧洞中圆弧段纵断面处模板的优化设计与精度分析[J].南水北调与水利科技,2010(4)：35-37.

[6]宁津生,刘经南,陈俊勇.现代大地测量理论与技术[M].武汉：武汉大学出版社，2006.

Study and Analysis on Coordinate Conversion by Application of Complex Number Calculation in Engineering Survey

YANG Weixing

(Northwest Engineering Corporation Limited, Xi'an710065，China)

Abstract:By application of mold, compound angle, rotation angle and scale parameter of the complex number, the mutual conversion between construction coordinates and geodetic coordinates is analyzed, studied and optimized reasonably. Accordingly, the simple formula applicable for the engineering application is derived, avoiding inconvenience resulted from the conversion factor between construction coordinates and geodetic coordinates in the engineering survey operation and improving work efficiency. Meanwhile, comparison, analysis and verification of relevant data by different calculation methods provides surveyors with reference.

Key words:complex number; scale parameter; construction coordinates; geodetic coordinates

中图分类号：P258

文献标识码：A

DOI:10.3969/j.issn.1006-2610.2016.02.007

作者简介：杨伟星(1979- )，男，河南省平顶山市人，工程师，从事电站的质量控制与变形观测工作.

收稿日期：2015-03-03

文章编号：1006—2610(2016)02—0024—03