多井不同时抽水试验求解水文地质参数解析法

滕　凯

( 齐齐哈尔市水务局，黑龙江省齐齐哈尔市　161006)



多井不同时抽水试验求解水文地质参数解析法

滕凯

( 齐齐哈尔市水务局，黑龙江省齐齐哈尔市161006)

摘要：针对利用多井不同时抽水试验资料求解水文地质参数采用试算法及特殊标准曲线比对法存在的计算过程繁复、人为误差难免、图表束缚严重等问题，采用优化拟合方法，在工程适应参数范围内，通过对以级数表示的泰斯井函数的简单函数替代，并依据抽水试验降深时间关系曲线上的选点，采用降深比值法。经对多井不同时抽水井流函数的整理推导，获得了可直接完成相关水文地质参数求解的一元二次方程，求解过程简捷直观，便于实际工程应用。精度分析表明，在工程适用参数范围内，最大误差小于3.31%，完全满足实际工程的计算精度要求。

关键词：多井；抽水；水文；地质；参数；优化拟合；水位降深比值；解析计算法

0前言

抽水井的试验资料是确定水文地质参数的主要依据，在透水性较强的含水层中进行抽水试验，采用单井抽水由于水位降深较小，所获得的水位降深曲线往往比较平缓，利用该曲线进行参数求解可能产生较大误差。为解决这一问题，实际工作中均采用多井抽水试验。另一方面，利用多井抽水试验也可有效消除单井抽水试验因机械设备或人为等其他因素对试验数据所产生的误差影响。因此，尽管多井抽水试验相对单井而言费用较大，但在实际水文地质工作中仍不失为一种较常采用的方法之一。多井抽水试验涉及2种井流条件，即分别为同时开泵和不同时开泵。关于利用多井同时开泵抽水试验资料求解水文地质参数的方法，已有较多研究成果[1-4]。本文仅对多井不同时开泵抽水试验求解水文地质参数的方法开展相关研究工作。

由于多井不同时开泵的井流函数为涉及多项属超越方程的泰斯井函数，不能通过常规的数学方法完成求解。目前，工程上主要采用试算法和特殊标准曲线比对法[5]。由于试算法需通过反复计算逐次逼近，求解过程十分繁复，不便实际工程应用；特殊标准曲线比对法由于需通过3条以上理论与实测降深曲线的反复比对分析，不但过程复杂，而且存在图上对比时的人为误差。为进一步简化该种抽水试验求解水文地质参数的获解方法，笔者依据优化拟合理论，对属超越方程的泰斯井函数进行了高精度替代，并根据降深比值关系，通过整理推导获得了求解相关水文地质参数的一元二次方程，由该方程可非常简捷地完成参数求解，计算过程简单直接，便于实际工程应用。

1公式的建立

1.1基本计算公式

在多井不同时开泵的作用下，含水层中任意一点的水位降深为：

(1)

其中:

式中：s为观测孔在抽水时间为t时的水位降深，m；Q1，Q2，…，Qn分别为按开泵时间顺序排列的各井出流量，m3/d；W(ui)为泰斯井流函数；ui为井函数自变量；t为从第1眼井开泵时刻起算的时间，d；t2，t3，…，tn分别为第2，3，…，n眼井开泵的时间，d；ri为观测孔到第i眼井的距离，m；T为含水层的导水系数，m2/d；α为含水层的压力传导系数，m2/d。

整理式(1)可得：

(2)

其中:t1=0。

根据多井抽水试验观测资料可完成实测水位降深与时间的关系曲线，即s～t曲线。在s～t曲线上分别选取A、B两点，即为(sA,tA)和(sB,tB)，将其分别代入式(2)可得：

(3)

(4)

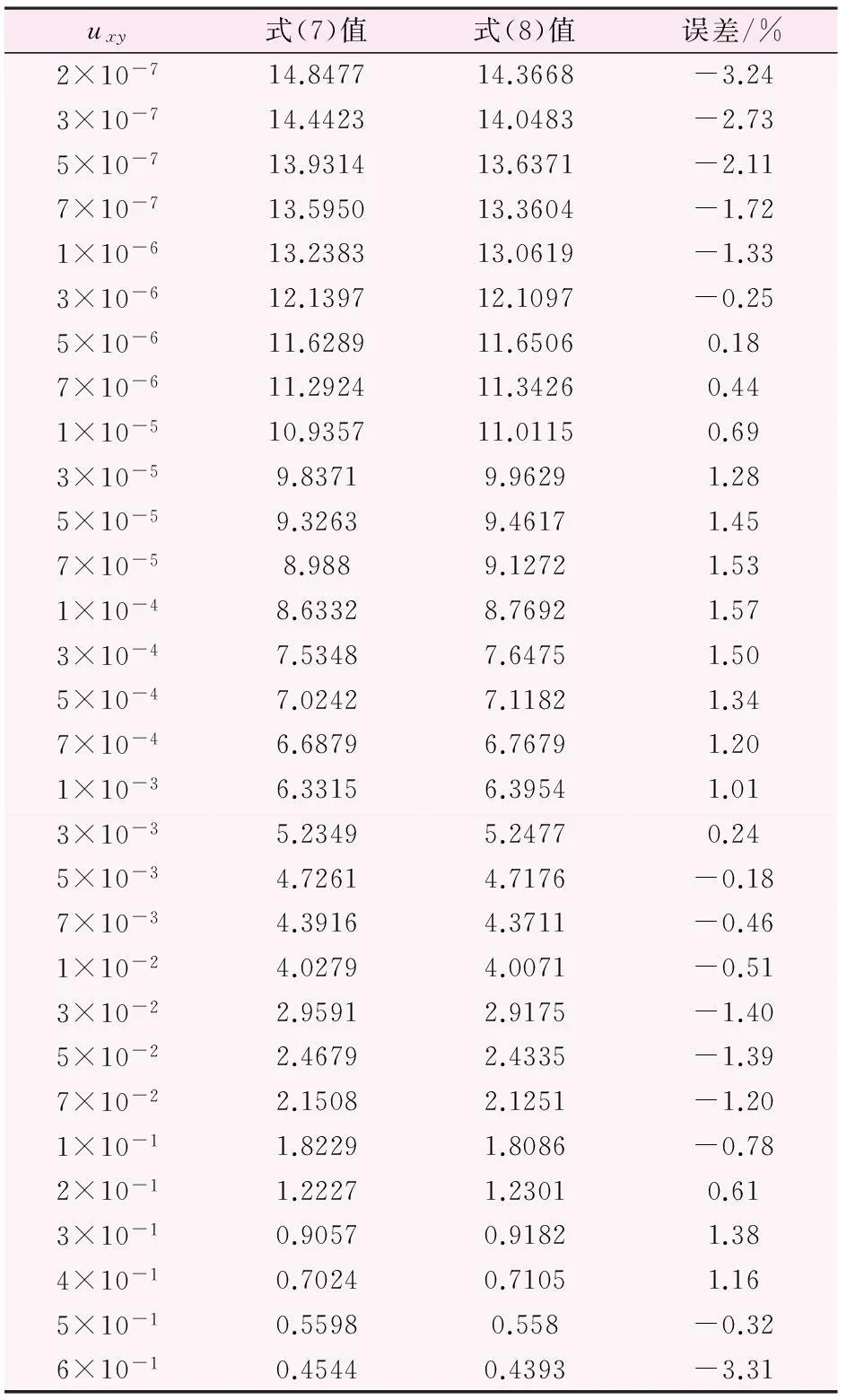
其中：tn

(5)

在式(5)中，因W(ui)为超越方程，只能通过设定不同的α，使等式两边相等的α即为所求值，α求出后即可用式(6)求得T值：

(6)

1.2简化计算公式

1.2.1泰斯公式的拟合

为避免利用式(5)求解待求参数必需采用试算之繁，现对式中的泰斯公式进行以下拟合替代。

泰斯井函数为一收敛级数，其表达式为：

(7)

设W′(ui)在工程适用参数范围内(即2×10-7≤ui≤0.6)可替代W(ui)，且满足将W′(ui)代入式(5)后可通过简单的数学方法直接完成待求参数的求解，实现多井不同时开泵抽水试验情况下水文地质参数的简化解析法求解。

根据对泰斯井函数标准曲线的线形分析，采用优化拟合方法，以标准剩余差最小为目标函数[6-8]，经对多个类似线形备选函数的拟合比选，求得泰斯井函数的最优拟合替代式为：

(8)

其中：A=18.76，B=-44.294，C=25.672。

在2×10-7≤ui≤0.6范围内，利用[W′(ui)-W(ui)]/W(ui)×100%即可完成式(8)替代式(7)的相对误差计算，结果见表1所示。由表1可见，式(8)的最大替代相对误差为3.31%，且发生在ui的值域端点，其他各点的相对误差均小于3.0%，其中相对误差小于2.0%的点占全部计算点的87%。可见，式(8)具有较好的替代精度，可以满足实际工程的计算要求。

1.2.2简化公式的建立

将式(8)代入式(5)，经进一步整理可得：

(9)

设：

(10)

(11)

(12)

(13)

则由式(9)经整理可得：

A1y2+B1y+C1=0

(14)

由式(14)解得y为：

(15)

进而可得α为：

(16)

α求出后即可利用式(6)求得T值。

2计算实例

选文献[5]算例：有3个不同时开泵的抽水井，相关试验数据见表2所示。

表2　抽水井相关数据表

根据观测孔的观测数据完成s～t曲线，并在s～t曲线上选取A、B、C三点，有关数据见表3所示。

表3　计算选点数据表

选A、B两点，因tA>tB>t3,则在s～t曲线上A、B两点所对应的观测孔的水位降深均受3眼井的抽水影响。

依据本文公式可得sAB=2.852 35，A1=1 196 151.400，B1=1 192 885.694，C1=285 321.175。将A1、B1、C1代入式(15)可得：

则由式(16)及式(6)即可分别求得含水层的压力传导系数α及导水系数T为：

采用同样方法也可完成选择A、C两点时的参数求解，所不同的是因tA>t3、t3>tC>t2，即为：观测孔降深sA受3眼井(1～3号井)抽水影响；sB受2眼井(1及2号井)抽水影响。其计算结果为：y=0.3975,α=1.019×105m2/d，T=500.0 m2/d。A、B及A、C两组求解结果的平均值为：α=1.01×105m2/d，T=499.0 m2/d，与文献[5]采用特殊标准曲线比对法求得的α=105m2/d，T=501.0 m2/d相比较，本文方法所求结果的相对误差分别为1.0%和0.2%。可见，本文方法具有较好的求解精度。

3结语

本文通过对多井不同时抽水井流函数中泰斯公式的优化拟合替代，解决了超越方程求解问题，并依据降深比值关系，实现了直接完成该种抽水试验条件下水文地质参数的求解。所获得的计算公式表达形式简单，求解过程不受图表束缚，避免了图表取值的人为误差及反复进行标准曲线比对的舍取之繁。

为有效消除观测孔的水位降深观测误差，在利用本文方法计算前，应根据观测孔的降深时间观测数据完成s～t曲线绘制，并对s～t曲线进行修正，剔除个别点的观测误差影响。

参考文献:

[1]胡云峰,李万月.干扰井群水文地质参数计算的简便公式[J].水文地质工程地质，1993(3)：23-24.

[2]滕凯,陈贺,屈凤海,等.干扰井群抽水试验资料推求水文地质参数的解析计算法[J].水利科技与经济，1995，1(1，2)：75-77，80.

[3]刘宇亨,刘微,林世波.干扰非稳定流抽水试验求解水文地质的新方法[J].黑龙江水利科技，2007，35(2)：28-29.

[4]高生,畅利毛,王鑫.潜水完整干扰井非稳定流抽水试验直线图解法[J].内蒙古水利，2011(1)：124-125.

[5]陈崇希,林敏.地下水动力学[M].武汉：中国地质大学出版社，1999.

[6]王慧文.偏最小二乘回归法及其应用[M].北京：北京国防工业出版社，1999.

[7]滕凯.利用降深比值求解越补水文地质参数简化方法[J].西北水电,2015(01): 24-27,41.

[8]阎凤文.测量数据处理方法[M].北京:原子能出版社，1988.

Analysis Method for Determination of Hydrogeological Parameters by Pumping Tests in Multiple Wells at Different Time

TENG Kai

(Qigihar Municipal Water Affairs Bureau, Qigihar, Heilongjiang161006，China)

Abstract:Trial method and special standard curve comparison applied for the hydrogeological parameters with data of pumping tests in multiple wells at different time feature the complicated calculation course, inevitable manual errors and severe diagram restriction. So, the optimum fitting method is applied. In range of the applicable engineering parameters and through the simple function substitution of Theis well function represented by stages, the water drawdown ratio method is applied based on the points selected from the drawdown-time curve of the pumping tests. Through the trimming and derivation of the flow functions of pumping wells at different time, a quadratic equation of one unknown which can be applied for direct determination of relevant hydrogeological parameters is obtained. The calculation course is simple, visual and convenient to apply in practice. The precision analysis demonstrates that the maximum error is lower than 3.31% in the range of the applicable engineering parameters, fully satisfying the requirement of the calculation precision of engineering practice.

Key words:multiple wells; water pumping; hydrology; geology; parameter; fitting optimization; water drawdown ratio; analysis and calculation method

中图分类号：P641.2

文献标识码：A

DOI:10.3969/j.issn.1006-2610.2016.02.005

基金项目：齐齐哈尔市科技攻关项目(NYGG201301)

作者简介：滕凯(1957- )，男，黑龙江省齐齐哈尔市人，高级工程师，主要从事水利防灾减灾及工程优化设计研究工作.

收稿日期：2015-03-03

文章编号：1006—2610(2016)02—0016—03